Призмы. Параллелепипед

Урок 20. «Призмы. параллелепипед»

Проверка домашнего задания

№ 718. 1)Представьте, что параллелограмм разрезали вдоль красного отрезка(рис. a и б) и из получившихся частей сложили прямоугольник. Каковы измерения этого прямоугольника? Чему равна площадь параллелограмма?

2)Составьте формулу для вычисления площади S параллелограмма( рис. в)

• а. 4- длина прямоугольника, 3 – ширина прямоугольника S=4*3=12(см 2 );

б. 5 – длина прямоугольника, 4 – ширина прямоугольника S=5*4=20 (см 2 );

2) S=а*b

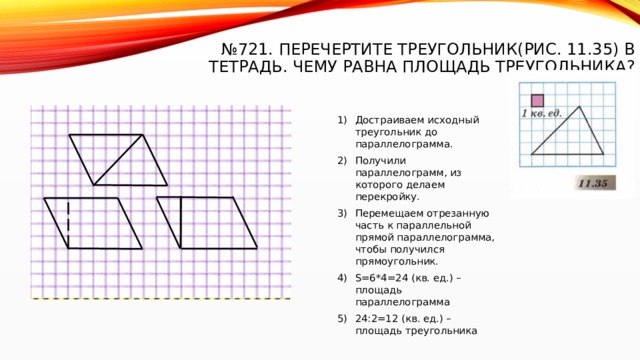
№ 721. перечертите треугольник(рис. 11.35) в тетрадь. Чему равна площадь треугольника?

• Достраиваем исходный треугольник до параллелограмма.
• Получили параллелограмм, из которого делаем перекройку.
• Перемещаем отрезанную часть к параллельной прямой параллелограмма, чтобы получился прямоугольник.
• S=6*4=24 (кв. ед.) – площадь параллелограмма
• 24:2=12 (кв. ед.) – площадь треугольника

№ 723. 1) От квадрата отрезали четыре равных треугольника(рис. 11.37). Найдите площадь оставшейся части. 2)Как вы думаете, какой фигурой является этот многоугольник?

1.

• 7*7=49 (см 2 ) – площадь всего квадрата
• ((3*4):2)*4= 24 (см 2 ) – площадь всех треугольников
• 49-24=25 (см 2 ) – площадь оставшейся части.

2.

Этот многоугольник является квадратом с стороной равной 5.

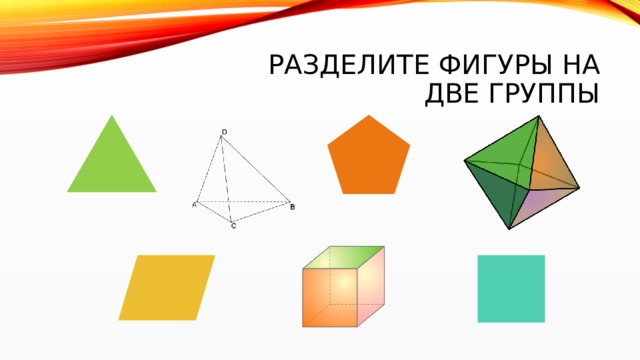
Разделите фигуры на две группы

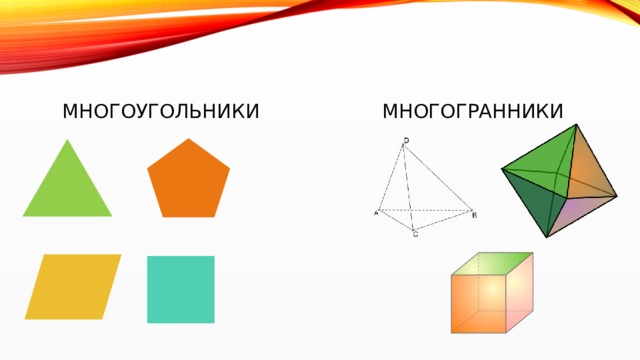
Многоугольники

Многогранники

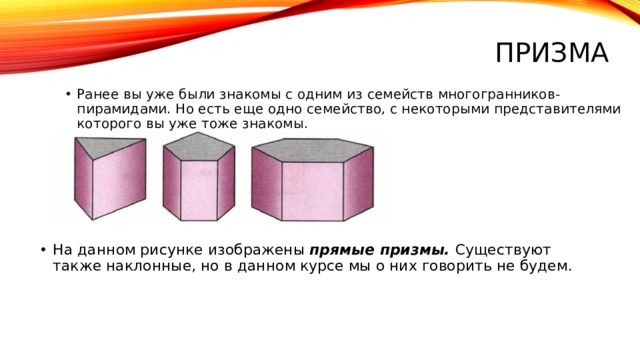
ПРизма

• Ранее вы уже были знакомы с одним из семейств многогранников- пирамидами. Но есть еще одно семейство, с некоторыми представителями которого вы уже тоже знакомы.

• На данном рисунке изображены прямые призмы. Существуют также наклонные, но в данном курсе мы о них говорить не будем.

Грани, ребра, вершины

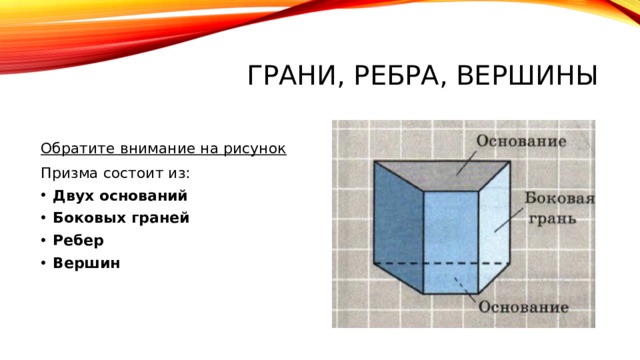
Обратите внимание на рисунок

Призма состоит из:

• Двух оснований
• Боковых граней
• Ребер
• Вершин

Основание призмы

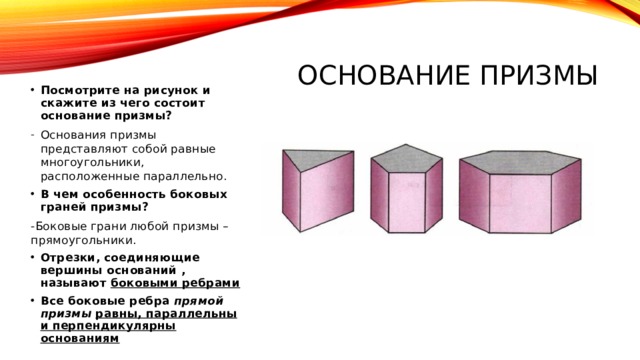
• Посмотрите на рисунок и скажите из чего состоит основание призмы?

• Основания призмы представляют собой равные многоугольники, расположенные параллельно.

• В чем особенность боковых граней призмы?

-Боковые грани любой призмы – прямоугольники.

• Отрезки, соединяющие вершины оснований , называют боковыми ребрами
• Все боковые ребра прямой призмы равны, параллельны и перпендикулярны основаниям

КАК называют разные призмы?

Треугольная

призма

Пятиугольная

Шестиугольная

призма

призма

• Мы определились, что основания разных прямых призм это различные многоугольники. Как же тогда называют каждую из таких призм?

- Призму называют по числу сторон многоугольника, лежащего в основании призмы.

• Если в основании призмы лежит правильный многоугольник , то такая призма называется правильной.

Параллелепипед

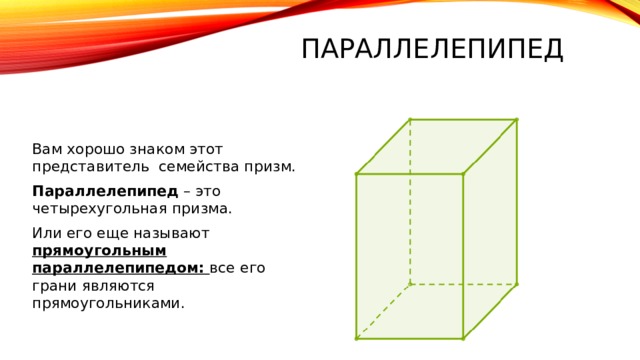
Вам хорошо знаком этот представитель семейства призм.

Параллелепипед – это четырехугольная призма.

Или его еще называют прямоугольным параллелепипедом: все его грани являются прямоугольниками.

Развертка призмы

• На прошлых уроках вы делали модели правильных многогранников из их развёрток.
• Ниже вы видите развёртку треугольной призмы, основания которой равнобедренные прямоугольные треугольники

Призмы в архитектуре

• Призмы часто использовались зодчими при возведении замков, башен, церквей.

Выборгский замок

Призмы в архитектуре

Афинская башня Ветров

Призмы в архитектуре

Канада. Монреаль. Жилой комплекс

На странице 218 учебника МАТЕМАТИКА. Арифметика. Геометрия. Автора Е.А. Бунимович, вы ещё раз можете ознакомиться с темой «Призма. параллелепипед».

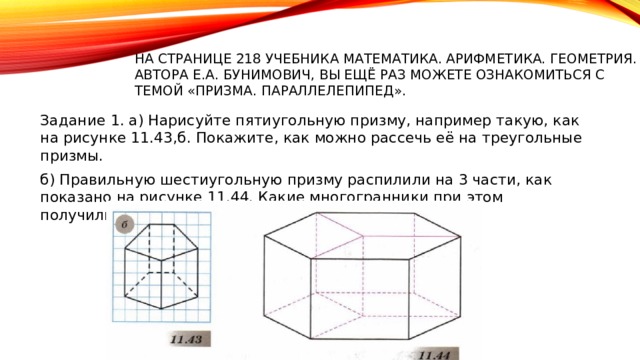
Задание 1. а) Нарисуйте пятиугольную призму, например такую, как на рисунке 11.43,б. Покажите, как можно рассечь её на треугольные призмы.

б) Правильную шестиугольную призму распилили на 3 части, как показано на рисунке 11.44. Какие многогранники при этом получились?

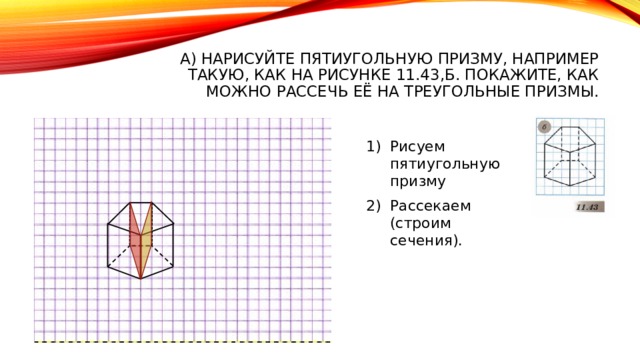
а) Нарисуйте пятиугольную призму, например такую, как на рисунке 11.43,б. Покажите, как можно рассечь её на треугольные призмы.

• Рисуем пятиугольную призму
• Рассекаем (строим сечения).

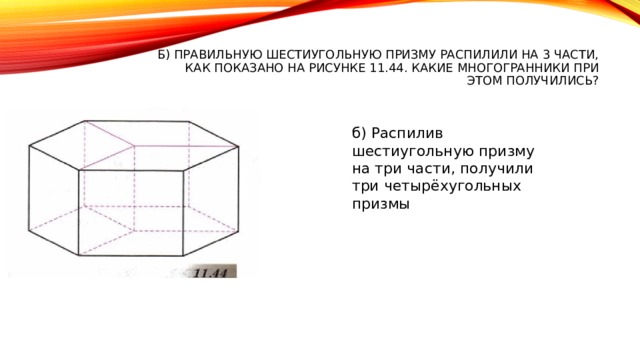
б) Правильную шестиугольную призму распилили на 3 части, как показано на рисунке 11.44. Какие многогранники при этом получились?

б) Распилив шестиугольную призму на три части, получили три четырёхугольных призмы

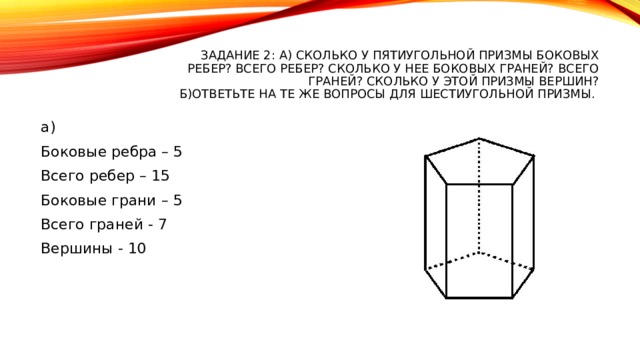
Задание 2: а) Сколько у пятиугольной призмы боковых ребер? Всего ребер? Сколько у нее боковых граней? Всего граней? Сколько у этой призмы вершин? Б)Ответьте на те же вопросы для шестиугольной призмы.

а)

Боковые ребра – 5

Всего ребер – 15

Боковые грани – 5

Всего граней - 7

Вершины - 10

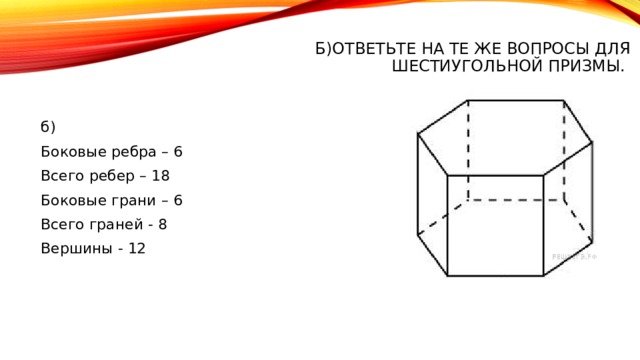
Б)Ответьте на те же вопросы для шестиугольной призмы.

б)

Боковые ребра – 6

Всего ребер – 18

Боковые грани – 6

Всего граней - 8

Вершины - 12

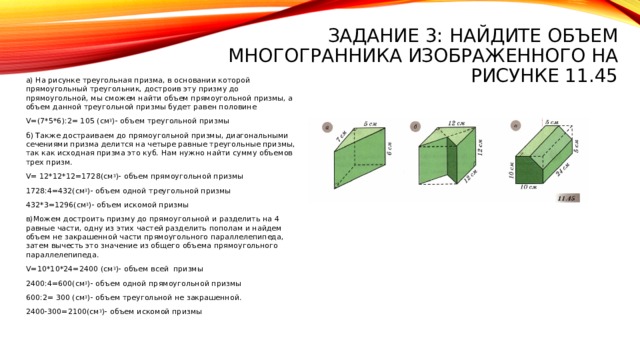
Задание 3: Найдите объем многогранника изображенного на рисунке 11.45

а) На рисунке треугольная призма, в основании которой прямоугольный треугольник, достроив эту призму до прямоугольной, мы сможем найти объем прямоугольной призмы, а объем данной треугольной призмы будет равен половине

V=(7*5*6):2= 105 (см 3 )- объем треугольной призмы

б) Также достраиваем до прямоугольной призмы, диагональными сечениями призма делится на четыре равные треугольные призмы, так как исходная призма это куб. Нам нужно найти сумму объемов трех призм.

V= 12*12*12=1728(см 3 )- объем прямоугольной призмы

1728:4=432(см 3 )- объем одной треугольной призмы

432*3=1296(см 3 )- объем искомой призмы

в)Можем достроить призму до прямоугольной и разделить на 4 равные части, одну из этих частей разделить пополам и найдем объем не закрашенной части прямоугольного параллелепипеда, затем вычесть это значение из общего объема прямоугольного параллелепипеда.

V=10*10*24=2400 (см 3 )- объем всей призмы

2400:4=600(см 3 )- объем одной прямоугольной призмы

600:2= 300 (см 3 )- объем треугольной не закрашенной.

2400-300=2100(см 3 )- объем искомой призмы

Закончите фразы

Домашнее задание

• К следующему уроку: параграф 47; №724, №729, №736
•   На следующем уроке мы обязательно проверим правильность выполнения домашних заданий.​