ГУ « Средняя общеобразовательная школа №5» отдела образования
акимата г. Костаная
ПЛАН-КОСПЕКТ УРОКА
ФИО (полностью) Пластун Сергей Владимирович
Предмет геометрия
Класс 8А-8 Б-1
Дата 12.09.17
Источники Алматы «Мектеп-2016»
Базовый учебник
Дополнительная литература
Признаки и свойства параллельных прямых. Сумма углов треугольника.
1. Цель урока: формировать умения применять полученные знания на практике
Задачи:
Образовательные:
- повторение, обобщение и проверка знаний по теме: «Признаки и свойства параллельных прямых. Сумма углов треугольника».
Развивающие:
- развить внимание, усидчивость, настойчивость, логическое мышление, математическую речь.
Воспитательные:
- посредством урока воспитывать активность ,внимательное отношение друг к другу, прививать умение слушать одноклассников.
2. Тип урока: обобщения и систематизации знаний
3. Формы работы с учащимися: фронтальная, индивидуальная.
4. Необходимое техническое оборудование.
5. Наглядные пособия, дидактические материалы, используемые на уроке.
6. Структура и ход урока.
СТРУКТУРА И ХОД УРОКА
| № | Этап урока | Деятельность учителя (например, иллюстрация, демонстрация и т. д.) | Деятельность ученика | Время (в мин.) |
| 1 | 2 | 3 | 4 | 5 |
| 1 | Организационный момент |
|
| 2 мин |
| 2 | Проверка домашнего задания |
|
| 2 мин |
| 3 | Актуализация опорных знаний |
| Отвечают на вопросы | 8 мин |
| 4 | Диагностика знаний и умений учащихся
|
| Работа у доски и в тетрадях | 18 мин |
| 5 | Подведение итогов |
|
| 3 мин |
| 6 | Постановка домашнего задания |
|
| 2 мин |
Ход урока
1. Организационный момент.
Проверка готовности класса к уроку. Сообщение темы и цели урока.
2. Проверка домашнего задания
3. Актуализация опорных знаний.
Теорема 1. Если при пересечении двух прямых секущей:
накрест лежащие углы равны, или
соответственные углы равны, или
сумма односторонних углов равна 180°, то
прямые параллельны (рис.1).

Следствие 1. Две различные прямые на плоскости, перпендикулярные одной и той же прямой, параллельны (рис.2).

Основное свойство параллельных прямых состоит в следующем.
Аксиома параллельных прямых. Через данную точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Рассмотрим некоторые свойства параллельных прямых, которые следуют из этой аксиомы.
1) Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую (рис.4).

Рис.4
2) Если две различные прямые параллельны третьей прямой, то они параллельны (рис.5).

Рис.5
Справедлива и следующая теорема.
Теорема 2. Если две параллельные прямые пересечены секущей, то:
накрест лежащие углы равны;
соответственные углы равны;
сумма односторонних углов равна 180°.
Следствие 2. Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой (см. рис.2).

Рис.2
4. Диагностика знаний и умений учащихся.
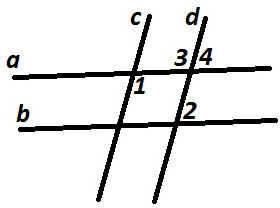
№1. (Фронтальная работа с классом)
Дано: а//в, какие из утверждений верные?
а//в=
а//в=
а//в=
а//в=
а//в=
а//в=
а//в=
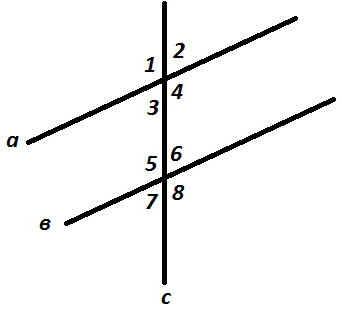
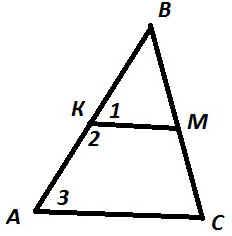
№2. Дано АС//КМ, какие из утверждений верны?(Учащиеся пишут номера верных равенств в тетрадях, затем меняются ими. Взаимопроверка.)
АС//КМ=
АС//КМ=
АС//КМ=
АС//КМ=
АС//КМ=
1. Две параллельные прямые пересечены третьей. Известно, что разность двух внутренних односторонних углов равна 30°. Найти эти углы.
Решение. Пусть условию отвечает рисунок 6.

Рис.6
Углы 1 и 2 внутренние односторонние, их сумма равна 180°, т. е.
∠ l + ∠ 2 = 180°. (1)
Обозначим градусную меру угла 1 через х. По условию ∠ 2 - х = 30°, или ∠ 2 = 30° + x.
Подставим в равенство (1) значения углов 1 и 2, получим
х + 30° + х = 180°.
Решая это уравнение, получим х = 75°, т. е.
∠ 1 = 75°, a ∠ 2 = 180° - 75° = 105°.
2. Две параллельные прямые пересечены третьей. Известно, что сумма двух внутренних накрест лежащих углов равна 150°. Чему равны эти углы и остальные шесть?
Решение. Пусть условию задачи соответствует рисунок 7.

Рис.7
Углы 1 и 2 внутренние накрест лежащие, следовательно, они равны. Сумма этих углов по условию задачи равна 150°, тогда ∠ 1 = ∠ 2 = 75°.
Найдем остальные углы (рис. 8):

Рис.8
∠ 1 = ∠ 3 = 75° и ∠ 2 = ∠ 7 = 75° (вертикальные). Углы 4 и 5, 6 и 8 равны как вертикальные, a ∠ 5 = ∠ 6 как внутренние накрест лежащие. Все перечисленные углы 4, 5, 6 и 8 равны между собой и равны по 105°, так как ∠ 4 + ∠ 3 = 180°, a ∠ 4 = 180° - ∠ 3.
Получили четыре угла по 75°, четыре угла по 105°
5. Подведение итогов.
Выставление оценок за урок.
6. Постановка домашнего задания. Повторить правила.
Дано а//в, c//d.