Проект " Готовимся к олимпиаде по математике"

Владея опытом точных наук

Изучим все, что есть в подлунном мире

Тогда лишь станет ясным все вокруг.

И понимание человеческое шире.

Адрес школы:

307207, Курская область,

Октябрьский район, с. Черницыно,

ул. Октябрьская, дом 458 – а

Телефон: 8 (47142) 2 – 12 – 24

Email: [email protected]

Сайт: oktr- cher.ru

муниципальное казенное общеобразовательное учреждение «Черницынская средняя общеобразовательная школа»

Октябрьского района Курской области

Готовимся к олимпиаде по математике

7 класс

2018 год

Градинар Александр, Морозова Ангелина, Цуканов Владислав, обучающиеся 7 «А» и 7 «Б» классов

Готовимся к олимпиаде по математике

Пособие для учащихся 7 класса

с. Черницыно

2018

Содержание

ВВЕДЕНИЕ 2

ГЛАВА I. Виды олимпиадных задач и методы

их решения 4

1.1. Принцип Дирихле. 4

1.2. Логические задачи. Истина или ложь 5

1.3.Инвариант 6

1.4.Задачи на взвешивание 7

1.5.Математическиеребусы 8

1.6.Задачи на разрезание 11

1.7.Задачи на составление уравнений 13

1.8.Математические игры 14

ГЛАВА II. Задания муниципального этапа Всероссийской

олимпиады школьников (Октябрьский район) 17

ЗАКЛЮЧЕНИЕ 23

СПИСОК ИНФОРМАЦИОННЫХ ИСТОЧНИКОВ 24

Введение

На уроке алгебры при изучении темы «Многочлены» учитель математики предложила нам задачу на делимость для работы в парах. После того, как одна из пар, справившаяся с решением задачи, объяснила решение остальным,учительница сказала, что задача эта олимпиадная. Чтобы решать такие задачи, надо развивать творческое мышление и тогда можнопоступить в престижный ВУЗ по результатам, полученным на олимпиадах. Поэтому школьники должны быть заинтересованы в том, чтобы научиться решать задачи повышенной сложности, которые предлагаются на олимпиадах различного уровня, но, как правило, не рассматриваются в школьном курсе.

Ещё она отметила, что с каждым годом сокращается количество участников муниципального этапа олимпиады по предметам физико-математического цикла, снижается результативность.

Мы решили выяснить, с чем это связано. И может ли размышление над трудной, нестандартной задачей доставлять радость и настоящее удовольствие.

Целью нашей работы является исследование и изучение основных типов олимпиадных задач, ознакомление с методами их решения.

Для достижения этой цели были поставлены такие задачи:

- изучить и понять типы олимпиадных задач;

- выявить отношение учащихся 7-9-х классов к такому виду задач;

- рассмотреть идеи и методы решения олимпиадных задач;

- создать пособие для подготовки к олимпиаде по математике.

Объект исследования: олимпиадные задачи (принцип Дирихле; задачи на разрезание; задачи на составление уравнений; логические задачи; инвариант; задачи на взвешивания; математические ребусы; математические игры).

Предмет исследования: методы и способы решения олимпиадных задач.

Гипотеза: знакомство с видами олимпиадных задач и методами их решения повысит интерес учащихся к принятию участия в них; способствует развитию компетентной личности, владеющей настойчивостью, инициативой, самостоятельностью.

В ходе работы над данной темой мы провели анализ результатов участия в муниципальном этапе олимпиады по математике обучающимися нашей школы; провели анкетирование среди обучающихся 7-9-х классов; изучили научную и учебную литературу; исследовали виды олимпиадных задач и методы их решений; научились решать такие задачи, создали пособие для подготовки к олимпиаде по математике для обучающихся 7-х классов.

На основании данных, предоставленных заместителем директора по УВР, мы составили таблицу результативности участия в муниципальном этапе Всероссийской олимпиады школьников по математике обучающихся МКОУ «Черницынская средняя общеобразовательная школа».

Учебный год	Кол-во победителей	Кол-во призёров
2012-2013 учебный год	3	2
2013-2014 учебный год	1	3
2014-2015 учебный год	2	1
2015-2016 учебный год	0	0
2016-2017 учебный год	0	0
2017-2018 учебный год	1	0

Из таблицы видно, что количество победителей и призёров муниципального этапа Всероссийской олимпиады школьников по математике за последние три года практически свелось к нулю.

Проведя анкетирование среди обучающихся 7-9-х классов с целью выявления отношения учащихся к олимпиадным задачам, мы выяснили, что 33% опрошенных семиклассников хотели бы участвовать в олимпиаде по математике. Самыми распространёнными объяснениями являются: желание проверить свои знания, любовь к математике, интерес. 66% не хотели бы участвовать в олимпиаде, объясняя это тем, что этот предмет им даётся сложно. Из 13 восьмиклассников 61% хотели бы попробовать свои силы, считают математику интересным предметом, помогающим развиваться и завлекающим интересными заданиями. На этот же вопрос утвердительно ответили 41% девятиклассников, мотивируя свой ответ тем, что понимают математику, 1 человек объяснил своё желание возможностью пропустить учебные занятия.

Анкета для обучающихся

Хотел (а) бы ты принять участие в олимпиаде по математике?

Ответ	7 класс (15)	8 класс (13)	9 класс (17)
Да (почему) Интересно Проверить свои знания Нравится математика Никак не объяснили Пропущу уроки Интересно и помогает развиваться	5 человек 1 1 1 2 0 0	8 человек 0 4 0 3 1 0	7 человек 1 3 2 0 1
Нет (почему) Нет желания Сложно даётся предмет Никак не объяснили Нет времени	10 человек 4 5 1 0	5 человек 2 3 0 0	10 человек 1 6 1 2

Глава 1. Виды олимпиадных задач и методы их решения.

1.1.Принцип Дирихле.

При решении различных математических задач применяется специальный метод, который называется “Принцип Дирихле”. Существует несколько формулировок данного принципа. Вот наиболее популярная: “Если в n клетках сидит m зайцев, причём m n, то хотя бы в одной клетке сидят по два зайца”.

Доказать данный принцип легко, методом доказательства от противного.

На первый взгляд непонятно, почему это совершенно очевидное предложение, тем не менее, является мощным математическим методом решения задач, причём самых разнообразных. Оказывается, всё дело в том, что в каждой конкретной задаче нелегко понять, что же здесь выступает в роли зайцев, а что - в роли клеток. И почему надо, чтобы зайцев было больше, чем клеток. Выбор зайцев и клеток часто неочевиден. Далеко не всегда по формулировке задачи можно определить, что следует применить принцип Дирихле. Главное же достоинство данного метода решения состоит в том, что он даёт неконструктивное решение (то есть мы знаем, что такие клетки есть, но где именно они находятся, часто указать не можем); попытка же дать конструктивное доказательство приводит к большим трудностям. Рассмотрим примеры различных задач, решаемых с помощью данного принципа.

Задачи с решениями

1. В классе 15 учеников. Докажите, что найдутся, как минимум, 2 ученика, отмечающие день рождения в одном месяце.

Решение: 15 учеников будут зайцами, а 12 месяцев в году - клетками. Так как 1512, то по принципу Дирихле найдётся, как минимум, одна клетка, к которой будут сидеть два зайца. То есть найдётся месяц, в котором свой день рождения будут отмечать по крайней мере 2 ученика.

1. Внутри равностороннего треугольника со стороной 1 см расположены 5 точек. Докажите, что расстояние между некоторыми двумя из них меньше 0,5 см.

Решение: Пусть 5 точек будут зайцами. Теперь надо выбрать, что будет клетками. Так как клеток должно быть меньше, и чаще всего на одну, то их должно быть 4. Но как получить эти 4 клетки? В задаче фигурируют числа 1 и 0,5; причём первое больше второго в 2 раза. Можно получить 4 клетки, разбив равносторонний треугольник с помощью проведения отрезков, соединяющих середины сторон. Тогда получим 4 равносторонних треугольника со сторонами по 0,5 см.

Так как зайцев больше чем клеток, зайцев пять, а клеток 4, и 54, то по принципу Дирихле найдётся клетка - равносторонний треугольник со стороной 0,5 см, в который попадут не менее 2 зайцев, то есть точек. Так как все 4 треугольника равны и расстояние между точками в любом треугольнике будет меньше, чем 0,5 см, то мы доказали, что как минимум между двумя точками расстояние будет меньше, чем 0,5 см.

1. Дано 12 целых чисел. Докажите, что из них можно выбрать 2, разность которых будет делиться на 11.

Решение: Числа будут зайцами. Так как их 12, то клеток должно быть меньше. Возьмём за клетки остатки от деления на 11. Всего клеток будет 11: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 , 10. Тогда по принципу Дирихле найдётся клетка, в которой будут сидеть по крайней мере два зайца, то есть найдутся два числа с одинаковым остатком. А разность двух этих чисел будет делится на 11. Действительно, пусть a=11m+q, b=11n+q, тогда a - b=11m+q - (11n+q)=11(m - n). А 11(m - n) делится на 11.

1. В ковре размером 3*3 м Коля проделал 8 дырок. Докажите, что из него можно вырезать коврик размером 1*1 м без дырок.

Решение: Для этой задачи нужна другая формулировка принципа Дирихле: “Пусть в n клетках сидят m зайцев, причём nm. Тогда найдётся хотя бы одна пустая клетка”.

Дырки здесь будут зайцами. Разрежем ковёр на 9 ковриков размером 1*1 м. Так ковриков-клеток 9, а дырок-зайцев 8, то найдётся хотя бы одна пустая клетка, в которой не будет зайцев, то есть дырок.

Реши сам

1. Дано 9 целых чисел. Докажите, что из них можно выбрать 2, разность которых делится на 8.

2. В классе 35 учеников. Можно ли утверждать, что среди них найдутся хотя бы два ученика, фамилии которых начинаются с одной буквы?

3. В лесу растёт миллион ёлок. Известно, что на каждой из них не более 600000 иголок. Докажите, что в лесу найдутся две ёлки с одинаковым количеством иголок.

1.2. Логические задачи. Истина или ложь

Логические задачи бывают разные. Мы остановимся на задачах по теме: “Истина или ложь”. Они довольно часто встречаются в олимпиадах по математике.

По самому названию задач понятно, что нужно в них делать - доказать, что определённое высказывание ложно или правдиво. Но как это сделать? Есть разные методы решения таких задач, но мы остановимся на двух основных:

1. С помощью таблицы

2. С помощью рассуждения

Объясним эти методы на примере следующих задач.

Задачи с решениями

1. Петя, Вася, Коля и Миша играли в футбол. Один из них разбил мячом стекло. На вопрос «Кто это сделал?» Петя, Вася и Коля ответили: «Не я», а Миша – «не знаю». Потом оказалось, что двое из них сказали правду, а двое – неправду. Знает ли Миша, кто разбил стекло?

Решение: Начнём с ответов Пети, Васи и Коли. Так как стекло разбил кто-то один, то среди ответов Пети, Васи и Коли может быть лишь один ложный, иначе при двух ложных ответах получается, что стекло разбили двое.

Тогда вторым ложным ответом будет ответ Миши, так как всего ложных ответов два. Поэтому Миша знал, кто разбил стекло.

1. На острове живут два племени: аборигены и пришельцы. Аборигены всегда говорят правду, а пришельцы лгут. Путешественник, приехавший на остров, нанял островитянина в проводники. Они пошли и увидели другого островитянина. Путешественник послал проводника узнать, к какому племени принадлежит этот туземец. Проводник вернулся и сказал: «Туземец говорит, что он абориген».

Кем был проводник: пришельцем или аборигеном?

Решение: Так как ответом встречного островитянина могла быть лишь фраза «Я – абориген» (этот ответ является правдой для аборигенов и ложью для пришельцев), а проводник сказал, что туземец – абориген, то проводник является аборигеном.

1. Четверо ребят – Алексей, Борис, Владимир и Григорий – участвовали в лыжных гонках. На следующий день на вопрос, кто какое место занял, они ответили так:

Алексей: я не был ни первым и не последним

Борис: я не был последним

Владимир: я был первым

Григорий: я был последним

Известно, что три из этих ответов были правдивыми, а один – ложью. Кто сказал правду? Кто был первым?

Решение: Предположим, солгал Алексей. Тогда получается, что он был первым или последним. Значит, солгали и Владимир, и Григорий. А это противоречит тому, что солгал один из ребят. Пусть солгал Борис. Тогда он был последним. Но Григорий также утверждал, что он был последним. Значит, данного случая также быть не может. Пусть солгал Владимир. Тогда он был не первым. В этом случае всё получается, и первым тогда будет Борис.

1. Беседуют трое: Белокуров, Чернов и Рыжов. Брюнет сказал Белокурову: «Любопытно, что один из нас русый, другой – брюнет, а третий – рыжий, но ни у кого цвет волос не соответствует фамилии». Какой цвет волос имеет каждый?

Решение: Здесь потребуется таблица размером 3*3.

Цвет волос Фамилия	Рыжий	Чёрный	Русый
Белокуров	+	-	-
Чернов	-	-	+
Рыжов	-	+	-

Реши сам

1. Александр, Борис, Виктор и Григорий – друзья. Один из них врач, другой – журналист, третий – спортсмен, а четвёртый – строитель. Журналист написал статьи об Александре и Григории. Спортсмен и журналист вместе с Борисом ходили в поход. Александр и Борис были на приёме у врача. Кто и какую профессию имеет?

2. В одном дворе живут 4 друга. Вадим и шофёр старше Сергея; Николай и слесарь занимаются боксом; электрик – младший из друзей; по вечерам Антон и токарь играют в домино против Сергея и электрика. Определите профессию каждого из друзей.

3. Как перевезти в лодке с одного берега реки на другой волка, козла и капусту, если известно, что волка нельзя оставить без привязи с козлом, а козёл неравнодушен к капусте? В лодке только два места, поэтому с собой можно брать только одно животное или только капусту.

1.3. Инвариант

Инвариантом некоторого преобразования называется величина или свойство, не изменяющееся при этом преобразовании. В качестве инварианта чаще всего рассматриваются чётность (нечётность)и остаток деления. Хотя встречаются и другие стандартные инварианты: перестановки, раскраски и т.п. Причём применение чётности - одна из наиболее часто встречающихся идей при решении олимпиадных задач. Идея чётности и нечётности при решении задач основана на двух очень важных утверждениях.

Лемма 1. Чётность суммы нескольких целых чисел совпадает с чётностью количества нечётных слагаемых.

Примеры:

1. Число 1+2+....+10 нечётное, так как в сумме 5 нечётных слагаемых.

2. Число 3+5+7+9+11+13 чётное, так как в сумме 6 нечётных слагаемых.

Лемма 2. Знак произведения нескольких (отличных от нуля) чисел определяется чётностью количества отрицательных сомножителей

Примеры:

1. Число (-1)*(-2)*(-3)*(-4) положительно, так как в произведении чётное число отрицательных сомножителей.

2. Число (-1)*2*(-3)*4*(-5) отрицательно, так как в произведении нечётное число отрицательных сомножителей.

Задачи с решениями

1. Учитель написал на листке число 10. 15 учеников передают листок друг другу, и каждый прибавляет к числу или отнимает от него единицу. Может ли в результате получится ноль?

Решение: После каждого перехода листка из рук в руки характер чётности числа будет меняться: после первого ученика число становится нечётным, после второго чётным, и т.д. Тогда после пятнадцатого ученика число будет нечётным. Поэтому ноль в конце получится не может

1. На доске написаны 15 чисел: 7 единиц и 8 нулей. Вам предлагается 14 раз подряд выполнить следующую операцию: зачеркнуть любые два числа, и если они одинаковые, то допишите к оставшимся числам нуль, а если разные - то единицу. Какое число останется на доске?

Решение: Сумма 15 исходных чисел равна 7. А 7- число нечётное. Рассмотрим, какая сумма чисел будет получаться после выполнения операции. Если вычеркнем 2 нуля, то на доске останется после дописывания нуля 9 нулей и 5 единиц. Сумма данных 14 чисел будет нечётной. Наконец, вычёркивая нуль и единицу и приписывая единицу, мы получим на доске 7 нулей и 7 единиц, сумма которых будет опять нечётным числом. Таким образом, мы замечаем, что после выполнения данной операции на доске получается на 1 число меньше, причём сумма оставшихся чисел всё время остаётся нечётной. Далее продолжаем эту операцию, то есть переходим от 14 чисел к 13 и т.д. Так как 1 - нечётное, а 0 - чётное, то на доске после выполнения 14 раз указанной операции получается нечётное число, то есть 1.

1. Все костяшки домино выложены в цепь (по правилам домино). На одном конце цепи оказалось 3 очка. Сколько очков на другом конце?

Решение: Всего имеется семь костяшек с тройкой на конце: 0-3, 1-3, 2-3, 3-3, 4-3, 5-3, 6-3. Костяшка 3-3 имеет тройку на обеих концах. Всего получается восемь троек. Так как по игре в домино в цепи должны располагаться парами, то на другом конце цепи будет 3 очка.

1. Квадрат размером 5*5 заполнен числами так, что произведение чисел в каждой строке отрицательно. Докажите, что найдётся столбец, в котором произведение чисел также отрицательно.

Решение: Так как произведение чисел в каждой строке квадрата отрицательно, то и произведение всех чисел будет отрицательно. Но, с другой стороны, произведение всех чисел равно произведению чисел в столбцах. А так как произведение всех чисел отрицательно, то найдётся столб, в котором произведение является отрицательным.

Реши сам

1. Можно ли купюру достоинством 50 рублей разменять на 15 монет с достоинством 5 и 1 рубль?

2. Конь вышел с поля a1 шахматной доски и через несколько ходов вернулся на него. Докажите, что он сделал чётное число ходов.

3. 2012 человек выстроились в шеренгу. Всегда ли можно их расставить по росту, если за один ход разрешается переставлять только 2 людей стоящих через одного?

4. 16 корзин расположили по кругу. Можно ли в них разложить 55 арбузов так, чтобы количество арбузов в любых двух соседних корзинах отличалось на 1?

1.4. Задачи на взвешивание

Математика - одна из древних и важных наук. Многими математическими знаниями люди пользовались ещё в глубокой древности - тысячи лет назад. Они были необходимы купцам и строителям, воинам и землемерам, жрецам и путешественникам. И в наши дни ни одному человеку не обойтись в жизни без хорошего знания математики. В данной работе рассматриваются задачи на «фальшивые монеты», задачи на уравнивания с помощью весов.

1. Имеются чашечные весы без гирь и две монеты, одна из которых фальшивая, причём легче другой. Требуется выявить фальшивую монету.

Решение: Положить по одной монете на каждую чашку весов. Фальшивая монета на той, которая вверху.

1. Имеется восемь одинаковых внешне монет, но одна из них фальшивая, она легче других. Требуется определить фальшивую монету. Какое минимальное количество взвешиваний потребуется?

Решение: Сначала взвешиваем по три монеты. Если весы уравновесились, то фальшивая монета находится среди двух. Её определяем вторым взвешиванием. Если весы уравновесились, то фальшивая монета среди трёх монет, находящихся на чашке весов, которая поднялась вверх. Её определяем вторым взвешиванием. Значит, мы на шли фальшивку за 2 взвешивания.

3. Дано 27 монет, одна из них фальшивая, она легче остальных. Можно ли найти фальшивую монету, выполнив 3 взвешивания?

Решение: Раздели монеты на три кучи по 9 монет и первым взвешиванием определим кучу, в которой фальшивая монета. Затем аналогично разделим 9 монет на три кучи и вторым взвешиванием определим кучку из 3 монет, в которой будет находится фальшивка. Третьим взвешиванием определим из этих трёх монет фальшивую.

1. Имеются чашечные весы без гирь и три монеты, одна из которых фальшивая, причём легче других. Требуется выявить фальшивую монету.

Решение: Положить две монеты на чаши весов, если они уравновесились, то фальшивая - оставшаяся; если не уравновесились, то фальшивая - на верхней чашке весов.

Реши сам

1. В четырёх мешках все монеты настоящие (весят по 10 г), а в одном все фальшивые (весят по 11 г). Одним взвешиванием на точных весах со стрелкой определите, в каком мешке фальшивая монета.

2. Имеются шесть одинаковых по виду монет, одна из которых фальшивая, причём легче других. Требуется определить фальшивую монету, совершив минимальное количество взвешиваний.

3. Имеются 7 одинаковых по виду монет, одна из которых фальшивая, причём легче других. Требуется определить фальшивую монету. Какое минимальное количество взвешиваний потребуется?

1.5. Математические ребусы

Слово “ребус” происходит от латинского слова “res” — “вещь”.

Суть ребуса — загадка, сформулированная в виде рисунка (либо фотографии) в сочетаниис буквами, цифрами, знаками, символами, фигурами.Решить ребус — значит “перевести” всё, что он содержит, в буквы, составляющие осмысленное слово или предложение.Первые ребусы появились во Франции в XV веке. В 1582 г. появился первый печатный их сборник. Автором его был Этьенн Табуро (1548—1590).Из Франции на ребусы перешла в Англию, Германию и Италию, но ни в одной изэтиx стран не получила широкого развития.В России они появились в 1845 г. в журнале "Иллюстрация".

В таких заданиях требуется расшифровать запись арифметического равенства, в котором разные цифры заменены буквами, причём разные цифры обозначены разными буквами, одинаковые - одинаковыми. Предполагается, что исходное равенство верно и записано по обычным правилам арифметики. В частности, в записи числа первая слева цифра не является цифрой 0; используется десятичная система счисления.

Правила разгадывания ребусов:

• Слово, изображённое на рисунке, не всегда читается полностью. Запятая слева от рисунка означает, что от его названия отнимается первая буква. Две или три запятые означают, что надо отнять две или три буквы. Запятые справа от рисунка отнимают последние буквы.

• Перевёрнутое изображение означает, что название надо читать наоборот. Кот вниз головой — «ток».

• Одна буква в другой говорит о том, что надо прибавить букву «В». Если внутри буквы «О» поместить «ДА», то получится «В-О-ДА».

• Если какая-нибудь буква составляется из других букв, то прибавляем «ИЗ». Например, если маленькими буквами "Б" изобразим большую "А", то получится "ИЗБА"

• Буква написанная поверх другой прибавляет «по».Например:«ПО-Р-Т», «ПО-Л-Е».

• Если буква написана над другой, то надо прибавлять «НА», «НАД» или «ПОД». Например: «фо-на-ри», «под-у-шка»

• Аналогично, если буква идет за буквой, то следует прибавить «ЗА». Например: «ЗА-Я-Ц», «КА-ЗА-НЬ».

• Нередко в ребусах изображаются ноты. Они заменяют соответствующие их названиям слоги.

К числовым ребусам можно отнести арифметические равенства. В последних все или некоторые цифры заменены буквами (или значками в числовых ребусах) какого-либо одного или различных алфавитов (включая системы счисления). Подобные ребусы представляют собой логико-математические задачи, в которых путём логических рассуждений и математических вычислений требуется расшифровать значение каждого символа и восстановить числовую запись. Причём перемена цифр (букв) чисел слева от

равенства между собой, как правило, не является новым решением (при отсутствии ограничений).

Можно выделить три основных типа ребусов, представленных в виде произведения, арифметической суммы, степени. Для каждого типа ребусов имеются некоторые общие правила их дешифровки. При решении ребусов, представленных в виде произведения,

необходимо учитывать:

• Нуль не может быть первой цифрой (ведущим).

• Если при умножении некоторого числа на однозначное получено исходное число, то множитель равен единице.

• Если при умножении некоторого числа, не оканчивающегося на нуль, на некоторое однозначное число, получен нуль в младшем разряде произведения, то младший разряд множимого и множителя есть пара чисел, одно из которых 5, а другое – число чётное.

• Если при умножении некоторого двузначного числа на некоторое однозначное число, большее 5, полученное произведение - двузначное число, тогда первая цифра множимого равна единице.

• Произведение некоторого числа, не оканчивающегося на нуль, на некоторое нечётное число даёт последнюю цифру (букву), равную последней цифре множимого тогда, когда цифра равна 5.

• Произведение некоторого числа, не оканчивающегося на нуль, на некоторое число, последняя цифра которого равна последней цифре (букве) множимого, даёт число, последняя цифра которого равна 5 или 1.

Например, найти все решения ребуса РЕ•ШЕ=НИЕ.1) 15•25=375; 2) 25•35=675;

3) 15•65=975; 4) 21•31=651.

При расшифровке числовых ребусов имеется много других закономерностей, связанных с их особенностями. Без системного и целенаправленного перебора, как правило, решения не находятся. Причём число рассматриваемых вариантов зависит от уровня, умений и навыков логико-математической подготовки, изобретательности и сообразительности ученика. Основные из этих закономерностей связаны с исходными цифрами множимого и множителя: а) 2•К (К от единицы до четырёх включительно) – не даёт переноса, например, МЕ•ДВ=ЕДЕВ. Решение: 41•32=1312. б) 2•6=2 – даёт перенос, например, РА•М=КА. Решение:12•6=72.

Способы решения ребусов, представленных в виде суммы:

• Метод уравновешивания с использованием табличного способа оформления логических дедуктивных умозаключений(рассуждений). Метод основан на решении уравнения в

• неотрицательных целых различных числах (буквах), как правило, отличных от нуля. Эквивалентное (исходному уравнению) уравнение получается переносом всех неизвестных в левую часть уравнения в порядке убывания абсолютных величин коэффициентов. Коэффициенты подбираются таким образом, чтобы левая часть уравнения была наиболее близка к нулю. При этом коэффициенты для различных букв должны различаться.

• Метод постепенного изменения букв в порядке возрастания коэффициентов. При этом целесообразно использовать табличный способ оформления логических заключений.

• Метод наибольшего общего делителя (НОД). Метод применяется, если только наименьший из коэффициентов не равен. Метод используется совместно с методом постепенного изменения значения букв в порядке возрастания коэффициентов.

• Очевидно, что получаемая сумма должна делиться на НОД коэффициентов при последующих слагаемых. При небольшом числе итераций по изменению значения букв (отбрасывания бесперспективных вариантов) и построении новой таблицы (изменением части первоначальной таблицы) получаем искомое решение.

Аналогичные способы решения ребусов применимы и для класса числовых ребусов, в которых для кодирования цифр применяется не буквенный символ (значок), заменяющий любую букву (чаще всего звёздочка). Большинство задач этого класса представляют собой ребусы в виде произведения чисел, в которых требуется вместо звёздочек подставить цифры. Решение этого класса ребусов требует, очевидно, меньшего количества логических высказываний (вариантов перебора), так в ребусе уже приведены некоторые цифры, упрощающее нахождение единственного решения. Например, РА•М=КА имеет следующие решения (без ограничивающих дополнительных условий) с использованием рассмотренных выше способов для ребусов, представленных в виде

произведения: 1) 12•6=72; 2) 15•3=45.

Аналогичный по формату числовой ребус **•6=*2 имеет только один вариант решения.

Логика и используемые способы решения:

1) шесть больше пяти, поэтому число десятков множимого равно единице; 2) число единиц множимого равно 2, так как если оно было бы равно 7 (7•6=42), то в этом случае имели бы: 17•6=102, то есть число трёхзначное, что противоречит условию. Итак, решение: 12•6=72.

Задачи с решениями

1.

2. 3.

4.В данном примере восстанови цифры, обозначенные звёздочками: *8*

4*2

7**

3**

****___

*****0

Решение.

Так как на конце результата цифра 0, то первый множитель оканчивается цифрой 5 или нулём, ибо при умножении на 2 нуль может получиться только от умножения 5 или нуля. По цифре 7 и множителю 2 определяем, что первый множитель начинается с цифры 3. По второму неполному произведению определяем, что вторая цифра второго множителя 1. Итак, первый множитель 385, второй 412 или первый 380, а второй 412.

Реши сам

1.Произведение первой цифры числа на оставшуюся часть равно57, а произведение последней цифры на оставшуюся часть числаравно 105. Найдите это число.

2.Какие цифры нужно поставить вместо А, В, С, Д в примере насложение АВСД+АВС+АВ+А=4321.

3.Из какого наименьшего числа «елок» может состоять «лесок»: ЕЛКА+ … +ЕЛКА =ЛЕСОК (одинаковыми буквами обозначены одинаковые цифры, разными

буквами - разные).

1.6. Задачи на разрезание

В задачах данного типа от нас требуют из определённых фигур сложить другую, при этом разными способами, или разрезать фигуру на части (в основном на равные). В ходе рассмотрения задач становится понятно, что какого-нибудь особенного метода решения здесь не существует, помогает лишь логическое и геометрическое мышление.

Задачи с решениями

1. Можно ли разрезать данную фигуру на 4 равные части?

Ответ: Да, можно.

2.Квадрат разрезали на два прямоугольника. Оказалось, что периметры обоих прямоугольников – целые числа. Можно ли сделать вывод, что периметр исходного квадрата также целое число?

Ответ: нет, нельзя.

Решение: Приведём такой пример: квадрат со стороной 5/6 разрежем на два прямоугольника длины 5/6 и ширины 1/6 и 4/6. Тогда периметры прямоугольников равны 2(1/6+5/6)=2 и 2(4/6+5/6)=3

3.Из листа клетчатой бумаги размером 8x8 клеточек Решение:

по линиям сетки вырезали 12 прямоугольников

1x2. Обязательно ли в оставшейся части можно

выделить клетчатый прямоугольник 1x3?

Ответ: нет, необязательно

4.Как разрезать данную фигуру на две части так, чтобы из них получился квадрат?

Решение:

Реши сам

1.Разрежьте данную фигуру на две части так, чтобы из них 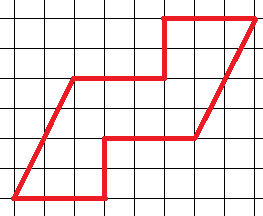получился квадрат.

2.Разрежьте фигуру на 4 равные части. 3.Разрежьте фигуру на 4 равные части.

1.7.Задачи на составление уравнений

Главная трудность при решении задачи на составление уравнений или систем уравнений в том, что по ее условию необходимо одну и ту же величину выразить двумя способами, а потом полученные выражения приравнять. Но какую именно величину – зависит от содержания задачи. К данному типу задач относятся задачи на движение, задачи на совместную работу (аналогом расстояния здесь является объем выполненной работы, а скорости движения – производительность труда), задачи на проценты и части и другие. При решении задач на проценты и части нужно помнить некоторые простые правила:

• Чтобы найти часть от числа, нужно эту часть умножить на число.

• Вся величина, от которой берутся проценты, составляет 100%.

• Чтобы избавиться от процентов, нужно перевести их в части, разделив на 100.

• Чтобы узнать, на сколько процентов изменилась какая-то величина, нужно из конечного значения вычесть начальное и результат разделить на начальное значение и умножить на 100%.

• Чтобы узнать процентное содержание вещества в растворе, нужно массу вещества разделить на массу раствора и умножить на 100%.

Задачи с решениями

1. Летели галки и сели на ветки. Если на каждую ветку сядет по галке, то одной галке не хватит ветки, а если на каждую ветку сядут по две галки, то одна ветка останется без галок. Сколько было веток и сколько галок?

Решение.

Пусть было x веток. Тогда число галок можно подсчитать двумя способами: 2(x – 1) или x + 1. Составим уравнение:2(x – 1) = x + 1, x = 3, x + 1 = 4. Ответ: 3 ветки и 4 галки

2.Турист отправляется в поход из А в В и обратно и проходит весь путь за 3 часа 41 минуту. Дорога из А в В идёт сначала в гору, потом по ровному месту и затем под гору. На каком протяжении дорога проходит по ровному месту, если скорость туриста составляет при подъёме в гору 4 км/ч, по ровному месту – 5 км/ч, а при спуске с горы – 6 км/ч, а расстояние между А и В 9 км?

Решение.

Пусть протяжённость дороги по ровному месту х км, тогда (9- х) км пути (в гору и под гору) турист проходит дважды (один раз со скоростью 4 км/ч, а другой раз – со скоростью 6 км/ч) и затрачивает на этот путь (9-х)/4 +(9- х)/6 часов. По ровному месту он затрачивает 2х/5часов. В оба конца турист затрачивает 3 ч 41 мин., т.е. 2х/5 +  (9-х)/4+(9- х)/6 =221/60. Решая это уравнение, получаем, что х=4(км).

Ответ: на протяжении 4 км дорога проходит по ровному месту.

3. Длину прямоугольника уменьшили на 10%, а ширину уменьшили на 20%. При этом периметр прямоугольника уменьшился на 12%. На сколько процентов уменьшится периметр прямоугольника, если его длину уменьшить на 20%, а ширину уменьшить на 10%?

Решение.

Пусть длина равна х, а ширина – у. Когда длину прямоугольника уменьшили на 10%, а ширину уменьшили на 20%, то периметр уменьшился на 2(0.1х+0.2у), что по условию составляет 12% от исходного периметра, т.е. 0.12Р=0.12•2(х+у). Получаем 2(0.1х+0.2у)= 0.12•2(х+у), откуда вытекает х=4у. Если длину уменьшить на 20%, а ширину уменьшить на 10%, то периметр уменьшится на 2(0.2х+0.1у)=2(0.2•4у+0.1у)=1.8у. Выразим исходный

периметр через у: Р=2(х+у)=2(4у+у)=10у. То есть исходный периметр уменьшится на 18%.

4. Свежие грибы содержат 90% воды, а сухие – 12% воды. Сколько получится сухих грибов из 44 кг свежих?

Решение.

По условию задачи 44 кг свежих грибов содержат 44•0,9=39,6 кг воды, а значит, сухого вещества 44-39,6=4,4 кг. Обозначим массу сухих грибов, которую можно получить из 44 кг свежих, через х кг. Эти х кг состоят из 0,12х кг воды и 0,88х кг сухого вещества. Так как

масса сухого вещества и в свежих, и в сухих грибах одна и та же, то 0,88х=4,4. Следовательно, х=5.

Ответ: 5 кг.

Реши сам

1.Между городами А и В через возвышенность ходит автобус. При подъёме на возвышенность он идёт со скоростью 25 км/ч, а при спуске – со скоростью 50 км/ч. От А до В автобус идёт 3,5 ч, а от В до А – 4 ч. Найти расстояние между городами А и В.

2.За весну Буратино похудел на 25%, затем за лето поправился на 20%, за осень похудел на 10%, а за зиму прибавил 20%. Похудел он в итоге или поправился?

3. В 10 т руды содержится некоторое количество железа. После удаления из неё 4 т примесей, содержащих 10% железа, процентное содержание железа в руде повысилось на 20%. Сколько железа осталось в руде?

4. Ученик при перемножении двух натуральных чисел, одно из которых на 94 больше другого, ошибся, уменьшив в произведении цифру десятков на 4. При делении, для проверки ответа, ошибочного произведения на больший из множителей он получил в частном 52, а в остатке – 107. Какие числа он перемножал?

1.8. Математические игры

Важным качеством любого человека является умение выбрать и обосновать лучший вариант своих действий, в каких бы то ни было условиях. Как играть, чтобы не проиграть (или игры со стратегией)?

Игры с решениями

1. Кто первым назовёт число 100.

Играют двое. Один называет любое целое число от 1 до 9 включительно. Второй прибавляет к названному числу любое целое число от 1 до 9 и называет сумму, к этой сумме первый вновь прибавляет любое целое число от 1 до 9 и называет новую сумму, и

т.д. Выигрывает тот, кто первым назовёт число 100.

Какие числа должен подбирать второй игрок, чтобы всегда выигрывать, независимо от числа, которое предлагает первый игрок.

Решение.

Нетрудно обнаружить способ игры второго, иначе говоря, стратегию второго, которая обеспечивает ему победу: «добавлять до числа, кратного 10». Если, к примеру, первый назвал 4, второй прибавляет 6 и называет сумму 10. Если первый прибавит 9 и назовёт

сумму 19, второй прибавит 1 и назовёт 20. Ясно, что как бы ни играл начинающий, второй при такой стратегии назовёт первым число 100. Если он хоть раз ошибётся, то этой стратегией неминуемо воспользуется первый и победит. Способ игры, обеспечивающий выигрыш одному из партнёров в любом случае, как бы ни играл его противник, называется выигрышной стратегией – это и есть секрет успеха, то есть «ключ к

победе», обладая которым можно выиграть у любого сколь угодно сильного противника.

2.На доске написано число 2000. Петя и Коля по очереди делят число, написанное на доске, на любое из следующих чисел: 2, 5, 10. Проигрывает тот из них, после хода которого на доске появится нецелое число. Петя ходит первым. Кто выигрывает при правильнойигре?

Решение.

Приведем выигрышную стратегию для Пети. Первым ходом он делит число 2000 на 5, после чего на доске написано 400. Далее на каждый ход Коли Петя отвечает таким же ходом, т.е. делит на то же число, что и Коля. Теперь заметим, что 400 – полный квадрат, а значит, после каждого хода Пети на доске вновь появляется квадрат некоторого натурального числа. Тогда после Колиного хода квадрата натурального числа появиться не может, а значит, не может появиться и единица. Следовательно, единица появится после хода Пети, т.е. Петя выигрывает.

3.«Математические загадки»
Кто-то читает загадку.  Команда поднимает сигнальную карточку, если готова ответить. За правильный ответ команда получает жетон. Если команда ошиблась, то есть шанс получить жетон у другой команды.

Проживают в трудной книжке
Хитроумные братишки,
Десять их, но братья эти
Сосчитают все на свете   (Цифры)

Могу назвать его мячом, 
А хочешь, дыркой назовём,
А можно бубликом,
Почти что кругленьким.  (Ноль)

Цифра, словно кочерга – 
У неё одна нога.                (Семь)

Эта цифра – акробатка, 
Если на голову встанет,
То другой она уж станет.  (Девять)

4.«Шифровка»
Подберите числа, назовите слова: 
МЕ + * (место)
*+ УМФ      (триумф )
Р + * + А (Родина)
*+ Я        (Семья)    

Реши сам

1. Игра дат

Первый игрок сообщает какую-нибудь дату января. Каждый игрок на своём ходе называет более позднюю дату, увеличивая каждый раз или календарную дату в месяце, или порядковый номер месяца, но не то и другое одновременно. Первый, кто доберётся до 31

декабря, выигрывает. Определить выигрышную стратегию для начинающего.

2. Поставь на ноль.

Возьмём полоску клетчатой бумаги и занумеруем клетки числами 0, 1, 2, …, 14. На одной из 15-ти клеток стоит фишка. Двое игроков по очереди передвигают фишку влево на 1, 2, 3 или 4 клетки. Проигрывает тот, кому некуда ходить. При каком начальном положении фишки выигрывает начинающий, а при каком его партнёр?

3.Малыш и Карлсон по очереди достают из коробки конфеты,при этом каждый берет на одну конфету больше или меньше, чемперед этим взял другой, не брать конфеты из коробки в свою очередьнельзя. Вначале в коробке было 24 конфеты, и Малыш и Карлсон

договорились, что если в какой-то момент в коробке останется ровно 4 или 14 конфет, то тому, чья очередь брать конфеты, достанется торт. Сможет ли Карлсон, который первым берет конфеты, выиграть торт, если вначале он имеет право взять 1 или 2 конфеты?

Глава II. Задания муниципального этапа Всероссийской олимпиады школьников (Октябрьский район)

2016-2017 учебный год

7.1.Существует ли четырёхзначное натуральное число с различными ненулевыми цифрами, обладающее следующим свойством: если к нему прибавить число, записанное теми же цифрами в обратном порядке, то получится число, делящееся на 101?

Решение:Достаточно привести пример такого числа. В действительности годится любое число, у которого сумма крайних цифр равна сумме средних цифр. Пример: возьмём число 1526, тогда 1526+6251=7777=101*77; или возьмём число 8967, тогда ; или, самое простое, возьмём число 1234, и т.п.

Ответ: существует.

7.2 Имеется 9 карточек с числами 1,2,3,4,5,6,7,8,9. (на каждой карточке написано одно число). Какое наибольшее количество этих карточек можно разложить в некотором порядке в ряд так, чтобы на любых двух соседних карточках одно из чисел делилось на другое?

Решение: Все 9 карточек положить в ряд требуемым образом не получится. В самом деле, число 5 делится только на 1, а из данных чисел на 5 ни одно не делится, поэтому у карточки 5 не может быть двух соседей в ряду, т.е. 5 должна стоять с краю, и соседом должно быть число 1. Аналогично, число 7 должно стоять с краю и соседствовать с 1. Все это вместе невозможно.

А вот 8 карточек требуемым образом положить можно, пример: 9, 3, 6, 2, 4, 8, 1, 5.

Ответ: 8.

7.3 В классе 26 учащихся. Они договорились, что каждым из них будет либо лжецом (лжецы всегда лгут), либо рыцарем (рыцари всегда говорят правду). Когда они пришли в класс и сели за парты, каждый из них сказал: «Я сижу рядом с лжецом». Затем некоторые учащиеся пересели за другие парты. Мог ли после этого каждый сказать: «Я сижу рядом с рыцарем»? Каждый раз за любой партой сидело ровно двое учащихся.

Решение: Фраза «Я сижу рядом с лжецом» могла быть произнесена только тогда, когда за одной партой сидят лжец и рыцарь. Это означает, что в классе поповну лжецов и рыцарей − по 13. Фраза «Я сижу рядом с рыцарем» может быть произведена только в том случае, когда за одной партой сидят либо два лжеца, либо два рыцаря. Но 13 − число нечётное, поэтому всех лжецов рассадить по двое за партой невозможно.

Ответ: не мог.

7.4 Белка в парке становится радостной, когда съедает по ореху трёх разных видов. Какое наибольшее количество белок Петя сможет сделать радостными, если он принёс в парк 20 бразильских орехов, 30 лесных, 40 грецких и 50 арахисовых?

Решение: Покажем сначала, как может действовать Петя, чтобы сделать радостными 45 белок. Начальная Петина позиция: Б-20, Л-30, Г-40, А-50 (Б-бразильские орехи, Л − лесные и п.т.). Пусть Петя сделает радостными 15 белок, выдав каждой из них по одному Б, одному Г и сумму А. Получается позиция Б-5, Л-30, Г-25, А-35. Пусть теперь Петя сделает радостными ещё 25 белок, выдав каждой из них по одному Л, одному Г и одному А. Получится позиция Б-5, Л-5, Г-0, А-10. Теперь Петя может сделать радостными ещё 5 белок, выдав каждой из них по одному Б, одному Л и одному А. Итоговая позиция: Б-0, Л-0, Г-0, А-5, и радостных белок.

Больше 45 радостных белок получить нельзя, как бы не действовал Петя. В самом деле, после 45-й выдачи (по три ореха каждая) остаётся орехов. При этом орехов А должно остаться не менее так как при каждой встрече используется не более одного ореха А. Это означает, что 45-я выдача орехов (если таковая случается) неизбежно приводит к позиции Б-0, Л-0, Г-0, А-5, и продолжение невозможно.

Ответ: 45.

7.5 Одно натуральное число больше другого на 4. Докажите, что их произведение не оканчивается на 31.

Решение: Пусть х − меньшее число. Тогда − большее число. Предположим, что их произведение оканчивается цифрами 31:

(многоточие − это предыдущие цифры, нам они не важны). Прибавим 4 к обеим частям равенства:

Но . Таким образом, число …35 является квадратом натурального числа. Мы видим, что оно делится на 5. Но если точный квадрат делится на 5, то он делится на.

Но наше число …35 на 25 не делится. Значит, исходное предположение неверно, и произведение не оканчивается на 31.

2015-2016 учебный год

7.1 Число 100 разделили на некоторое число, меньшее 50, с остатком, равным 6. На какое число могло произойти деление?

Решение: Пусть х – число, на которое делили, m- неполное частное: 100=m*x+6 (так как 6 остаток, то х6, тогда m2, так как хm*x=94=2*47. Отсюда видно, что числа mиx есть как раз числа 2 и 47, т.е. m=2, х=47. (т.к. число 94 только четырьмя способами можно представить в виде произведения двух натуральных чисел: 1*94, 94*1, 2*47, 47*2, то отпадают все способы, кроме 2*47).

Ответ: 47.

7.2 На доске написано несколько чисел. Разрешается стереть два числа Xи Y и написать вместо них X-2 и Y+1. Докажите, что после нескольких таких операций на доске обязательно появится отрицательное число.

Решение: Будем следить за суммой S всех чисел на доске. Каждая операция (x, y) = (x-2, y+1) уменьшает Sна единицу. Поэтому через некоторое число операций сумма S станет отрицательной. Значит, среди чисел на доске есть отрицательные.

7.3 Автобус идёт под гору со скоростью 30 км/час, а в гору – со скоростью 15 км/час. На дороге между двумя посёлками нет горизонтальных участков, а дорога автобуса туда и обратно занимает ровно 4 часа. Найдите расстояние (по дороге) между посёлками.

Решение: Рассмотрим любой наклонный участок дороги, пусть его длина L. При движении в одном направлении автобус идёт по этому участку под гору, а при движении в обратном направлении – в гору. Время автобуса на проезд этого участка туда и обратно составляет: L/15+L/30=3L/30=L/10. Просуммировав по всем наклонным участкам, найдём, что общее время – туда и обратно – равно S/10, где S– расстояние (по дороге) между посёлками. Таким образом, S/10=4, S=40.

Ответ: 40 км.

7.4 Можно ли расставить в клетках таблицы 5х8 числа 1 и 3 так, чтобы в каждой строке и в каждом столбце сумма чисел делилась на 7?

Решение: Предположим, что удалось так расставить числа 1 и 3 в таблице, что их сумма в каждой из 5 строк и в каждом из 87 столбцов делится на 7. Сумма в любой строке не меньше 8*1=8 и не больше 8*3=24. Числа в промежутке от 8 до 24, делящиеся на 7, это 14 и 21. Заметим, что сумма чисел в строке чётна – это сумма восьми нечётных чисел 1 и 3. Следовательно, в каждой строке сумма равна 14. Аналогично, сумма чисел в каждом столбце лежит в промежутке от 5 до 15, является нечётной и делится на 7, т.е. эта сумма равна 7. Подсчитаем сумму S всех чисел в таблице:

1. По строкам: S=14*5=70;

2. По столбцам: S=7*8=56. Полученное противоречие свидетельствует о том, что предположение о возможности, требуемой в условии задачи расстановки чисел неверно. Так расставить числа нельзя.

Ответ: нельзя.

7.5 Вокруг круглого стола сидят 39 человек – каждый либо рыцарь, либо лжец. Рыцарь всегда говорит правду, а лжец всегда лжёт. Каждого из них спросили: «Кто сидит справа от тебя?» Могло ли быть получено 37 ответов «лжец» и 2 ответа «рыцарь»?

Решение: Предположим, что могло. Всевозможные пары соседей (слева направо): ЛР (т.е. лжец, рыцарь), РЛ, ЛЛ, РР. Пары ЛР и РЛ дают ответ Л, а пары ЛЛ и РР дают ответ Р. Заменим все Л на числа -1, а все Р на числа 1. Тогда ответ для пары соседей – это их произведение. Итак, есть 37 пар соседей с ответом – произведением, равным -1, и 2 пары соседей с ответом – произведением, равным 1. Рассмотрим произведение всех ответов. Оно равно ((-1)*37)*(1*2)=-1. С другой стороны, произведение всех ответов – произведение произведений всех пар соседей, а в это произведение каждое число входит дважды (каждое число участвует в двух парах). Поэтому это произведение равно 1. Противоречие. Ответ: нет.

2014-2015 учебный год

7.1 Найдите углы прямоугольного треугольника, если известно, что один его угол в 5 раз больше другого.

Решение: Два варианта ответа: 1) 90 градусов, 90/5=18 градусов, 90-18=72 градуса, если больший угол – это прямой угол. 2) 90 градусов, 15 градусов, 75 градусов, если углы из условия задачи – это острые углы, так как х+5х=90 градусов, х=15 градусов, 15*5=75 градусов.

Ответ: 1) 90,18, 72 градусов; 2) 90, 15, 75 градусов.

7.2 На дискотеку собрался весь класс – 22 человека. Аня танцевала с 7 мальчиками, Белла – с 8, Вера – с 9 и так далее, причём последняя из девочек танцевала со всеми мальчиками. Сколько мальчиков было на дискотеке?

Решение: Пусть m– число мальчиков, d=22-m – число девочек.По условию, i-ая по счёту девочка танцевала с (i+6)-ю мальчиками. Таким образом, последняя d-ая девочка танцевала с (d=6)-ю мальчиками, т.е. d+6=m. Значит, 22-m+6=m, 2m=28, m=14.

Ответ: 14 мальчиков

7.3 Два автомобиля одновременно выехали из пунктов А и В навстречу друг другу. Через 7 часов езды расстояние между ними было 136 км. Найдите расстояние между А и В, если всё расстояние один автомобиль проезжает за 10 часов, а другой за – 12 часов.

Решение: Пусть 1-ый автомобиль выезжает из А и всё расстояние преодолевает за 10 ч. Через 7 часов он оказывается в точке А₇, причём АА₇=(7/10)S(1/2)S. Аналогично ВВ₇=(7/12)S(1/2)S. Имеем: ВВ₇=BA₇+A₇B₇=(3/10)S+136, т.е. (7/12)S=(3/10)S+136, (7/12)S-(3/10)S=136, ((35-18)/60)S=136, (17/60)S=136, S=36*(60/17)=8*60=480.

Ответ: 480 км.

7.4 В клетках квадрата 5х5 расставлены числа так, что во всех строках и во всех столбцах сумма чисел одинаковая. В верхнем правом квадрате 2х2 сумма чисел оказалась равной 10, а в левом нижнем квадрате 3х3 сумма оказалась равной 15. Найдите сумму всех чисел в квадрате.

Решение: Обозначим через S сумму чисел в любой строке и в любом столбце. Пусть х – сумма чисел в верхнем левом прямоугольнике 2х3 (две строки, три столбца). Складывая числа 1-й и 2-й строк, получим х+10=2S. Складывая числа 1-ого, 2-ого и 3-его столбцов, получим х+15=3S. Отсюда находим S=5. Поэтому сумма всех чисел в квадрате равна 5*5=25.

Ответ: 25.

7.5 Может ли число, являющееся произведением четырёх последовательных натуральных чисел, оканчиваться цифрами 2014 (именно в таком порядке)?

Решение: Среди четырёх последовательных натуральных чисел есть два чётных числа. Поэтому их произведение делится на 4. А число, оканчивающееся цифрами 2014, на 4 не делится.

Ответ: не может.

2013-2014 учебный год

7.1 Докажите, что если xи y положительные числа, то хотя бы одно из чисел x, y и 1/0^~+0` больше числа 0,7.

Решение: Если среди x иy есть число, большее 0,7, то и доказывать нечего. Если же x0,7 и y0,7, то x + y1,4 и 1/x + y1/1,40,7.

7.2 Петя рисует прямоугольные треугольники так, чтобы их площади выражались целыми числами, а длины катетов были не меньше 90, но и не больше 100. Он нарисовал 952 треугольника. Докажите, что среди треугольников есть равновеликие (т.е. с равными площадями).

Решение: Площадь S прямоугольного треугольника с катетами aиb выражается формой S=1/2ab. У Пети катеты aиb лежит в пределах 90 a, b100. Поэтому площади Петиных треугольников лежат в пределах от 1/2*100*100=5000. Но площади этих треугольников, по условию – целые числа. На промежутке (4050; 5000) находится 951 целое число. Но Петиных треугольников 952. Поэтому среди этих треугольников неизбежны треугольники с равными площадями.

7.3 Докажите, что если натуральные числа mи n взаимно просты (т.е. не имеют общего делителя 1), то число m*n не делится на число m+n.

Решение: Предположим, что m*n делится на m+n, т.е. m*n=(m+n)t, гдеt – натуральное число. Тогда m*(n-t)=n*t. Левая часть последнего равенства делится на m; значит и правая часть должна делиться на m. Но nи m не имеют общих делителей, кроме 1, поэтому на mделится число t. Поэтому tm, но тогда m*n=m*t+n*tn*tm*n – невозможное равенство. Следовательно, исходное предположение о том, что m*nделится наm+n неверно.

7.4 Диагонали АС и ВД выпуклого четырёхугольника АВСД пересекаются в точке О и взаимно перпендикулярны. На луче ДА взята точка Е такая, что АЕ=АВ, и точка А лежит между точками Д и Е. Пусть М середине отрезка ВЕ. Докажите, что угол ВАМ равен углу ВОМ.

Решение: Треугольник ВАЕ равнобедренный АВ=АЕ. В этом треугольнике медиана АМ является высотой. Стало быть, угол АМВ прямой. Рассмотрим окружность, для которой АВ является диаметром. Точки М и О лежат на этой окружности (ГМТ, из которых отрезок АВ виден под прямым углов, представляет собой окружность с диаметром АВ). Углы ВАМ и ВОМ вписанные и опираются на одну и ту же дугу ВМ. Значит, они равны.

7.5 На смотре войска Острова Лжецов и Рыцарей (лжецы всегда лгут, рыцари всегда говорят правду) вождь построил всех воинов в шеренгу. Каждый из воинов, стоящих в шеренге сказал: «Мои соседи по шеренге – лжецы» (воины, стоящие в концах шеренги сказали:«Мой сосед по шеренге – лжец»). Какое наибольшее число лжецов могло оказаться в шеренги, если на смотр вышли 1000 воинов.

Решение: Рассмотрим двух воинов, стоящих рядом в конце шеренги. Оба они не могут оказаться лжецами. Поэтому из четырёх воинов, стоящих в концах шеренги (по два с каждой стороны), не более двух лжецов. Рассмотрим любых трёх подряд стоящих воинов. Все они не могут оказаться лжецами (иначе средний сказал правду). Значит, среди трёх подряд стоящих воинов не более двух лжецов. В итоге лжецов всего не более, чем 2+(1000-4)\3*2=666. Приведём пример, в котором лжецов действительно ровно 666:

(ЛР)(ЛРЛ)(ЛРЛ)(ЛРЛ)…(ЛРЛ)(РЛ).

2012-2013 учебный год

7.1Найдите какое-нибудь натуральное число такое, что если к нему прибавить сумму его цифр, то получится 2222.

Решение: 2209+(2+2+0+9)=2222

Ответ: 2209

7.2 Мама купила 10 больших пирожных, 7 средних и 4 маленьких. Маленькое пирожное весит вдвое меньше среднего, а большое – втрое больше маленького. Как маме поделить их между шестью детьми, чтобы общий вес пирожных, доставшихся каждому, был одним и тем же, если разрезать пирожные она не хочет?

Решение: Пусть m – вес маленького пирожного, тогда среднее весит 2m, а большое – 3m. Общий вес всех пирожных равен: 4*m+7*2m+10*3m=48m, поэтому одному ребёнку должны достаться пирожные общим весом 8m.

Ответ: Например: пятерым дать по два больших пирожных и одному среднему, а шестому – два средних и все четыре маленьких.

7.3 Поезд, двигаясь с постоянной скоростью, к 17:00 проехал в 1,2 раза больший путь, чем к 16:00. Когда поезд выехал?

Решение: Если путь, пройденный поездом к 16:00 – это S, то к 17:00 он проехал путь 1,2*S , то есть путь длины S он проезжает за 5 часов. Начальное время движения – 16-5=11 часов.

Ответ: В 11:00

7.4Как разрезать клетчатый квадрат размеров 6х6 клеточек на четыре одинаковые фигуры периметра 16 каждая, если резать можно только по сторонам клеточек? Сторона клеточки равна 1.

Решение:

7.527 одноклассников ели конфеты на первой и второй переменах, причём на второй перемене каждый съел на одну конфету больше, чем на первой. Петя сказал, что он посчитал общее количество съеденных конфет и получил ответ 210. Правильно ли он посчитал?

Решение: Сумма двух последовательных чисел – это сумма двух чисел разной чётности, а потому нечётна. Значит, каждый из одноклассников съел нечётное число конфет. Одноклассников – нечётное количество (27), а сумма нечётного количества нечётных чисел – нечётна и не может равняться 210.

Ответ: Петя ошибся

Заключение

Данная работа посвящена решению олимпиадных задач. В этой работе рассмотрен далеко не полный круг элементарных олимпиадных задач. Чем больше мы изучали научную литературу, тем больше открывали для себя насколько велико их разнообразие. Мы считаем, что эта работа предназначена для обучающихся 7-ых классов, хотя она может оказаться полезной и для школьников возрастом постарше.

В ходе работы над данной темой мы пришли к выводам:

• Умение решать задачи, особенно олимпиадные, является одним из показателей развитости математического мышления. При решении задач, в первую очередь, важны математическая правильность, рациональность решения, а также аккуратность и подробность. Мы убедились, что самостоятельная работа над решением задач приносит пользу и помогает подготовиться к занятиям математикой.

• Умение решать такие задачи помогает развивать логическое мышление, сообразительность, наблюдательность, смекалку, что пригодится при изучении трудных тем по математике в старших классах.

Список информационных источников

1. Агаханов Н.Х., Богданов И.И., Кожевников П.А., Подлипский О.К.,

Терешин Д.А. Математика. Всероссийские олимпиады. Вып. 1. – М.:

Просвещение, 2008

2. Агаханов Н.Х., Подлипский О.К. Математика. Всероссийские

олимпиады. Вып. 2. – М.: Просвещение, 2009.

3. Глейзер Г.И. История математики в школе: 5-7 кл. – М.: Просвещение, 1981.

4. Гусев В. А., Орлов А.И., Розенталь А.Л. Внеклассная работа по математике в 6-8 классах. Под ред. С. И. Шварцбурда. М., «Просвещение», 1977.

5. Нагибин Ф. Ф., Канин Е. С. Математическая шкатулка: Пособие для учащихся. – 4-е изд., перераб. и доп. - М.: Просвещение, 1984.

6. Петраков И.С. Математические олимпиады школьников. – М.:

Просвещение, 1982.

7. Фарков А.В. Математические олимпиады: методика подготовки и проведения. – М.: ВАКО, 2017.

Интернет-ресурсы:

http://math-on-line.com - Математика-он-лайн. Занимательная

математика школьникам.

http://school-collection.edu.ru – единая коллекция цифровых

образовательных ресурсов (задачи Московских олимпиад

классифицированные по темам).