Проект "Многоугольники"

ГБПОУ АО «Котласский транспортный техникум»

Индивидуальный проект по теме:

«Построение правильных многоугольников»

Выполнил: обучающийся 1 курса

группа № 296

Михайлов Богдан Владимирович

Проверил: преподаватель математики

Е.Н. Витязева

пос. Вычегодский

2017 год

Содержание

1.Введение

2. Определение правильного многоугольника.
2.Треугольник

3.Квадрат

4.Пятиугольник

5. Пентаграмма

6.Шестиугольник

7.Гексаграмма

8.Правильные восьмиугольник (октагон)

9.Семиугольник

10.Гептаграмма

11.Октаграмма
12.Девятиугольник

13. Заключение.

14.Список литературы.

Введение

Цель проекта - изготовить наглядное пособие по теме "Построение правильных многоугольников".

Задачи:

1. Изучить литературу по данной теме.

2. Отобрать материал для выполнения проекта.

3. Познакомиться с видами правильных многоугольников.

4.Изучить способы построения некоторых правильных многоугольников.

5. Подготовить презентацию для защиты проекта.

Актуальность.

При изучении предмета геометрия очень важно уметь правильно и красиво выполнять чертежи как для решения задач так и для самостоятельного изображения геометрических фигур. В школьном курсе изучаются обычно 3 вида правильных многоугольников: равносторонний треугольник, квадрат, правильный шестиугольник. Моя работа поможет расширить студентам сведения о правильных многоугольниках и поддержать интерес к изучению геометрии.

Определение правильного многоугольника.

Пра́вильный многоуго́льник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между смежными сторонами равны.

Определение правильного многоугольника может зависеть от определения многоугольника: если он определён как плоская замкнутая ломаная, то появляется определение правильного звёздчатого многоугольника как невыпуклого многоугольника, у которого все стороны между собой равны и все углы между собой равны.

На рисунке представлены некоторые правильные многоугольники.

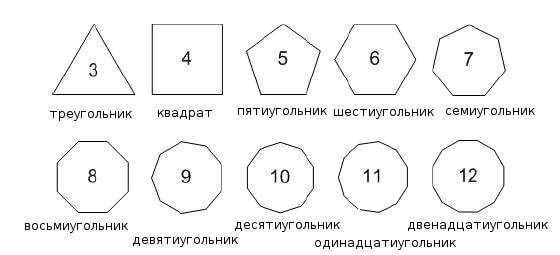
Построение правильного многоугольника с n сторонами оставалось проблемой для математиков вплоть до XIX века. Такое построение идентично разделению окружности на n равных частей, так как соединив между собой точки, делящие окружность на части, можно получить искомый многоугольник.

Эвклид в своих «Началах» занимался построением правильных многоугольников в книге IV, решая задачу для n = 3, 4, 5, 6, 15. Кроме этого, он уже определил первый критерий построимости многоугольников: хотя этот критерий и не был озвучен в «Началах», древнегреческие математики умели построить многоугольник с 2^m сторонами (при целом m 1), имея уже построенный многоугольник с числом сторон 2^{m — 1}: пользуясь умением разбиения дуги на две части, из двух полуокружностей мы строим квадрат, потом правильный восьмиугольник, правильный шестнадцатиугольник и так далее. Кроме этого, в той же книге Эвклид указывает и второй критерий: если известно, как строить многоугольники с r и s сторонами, и r и s взаимно простые, то можно построить и многоугольник с r · s сторонами. Синтезируя эти два способа, можно прийти к выводу, что древние математики умели строить правильные многоугольники с 2 m ⋅ p 1 k 1 ⋅ p 2 k 2 {\displaystyle 2^{m}\cdot {p_{1}}^{k_{1}}\cdot {p_{2}}^{k_{2}}} сторонами, где m — целое неотрицательное число, p 1 , p 2 {\displaystyle {p_{1}},{p_{2}}}  — числа 3 и 5, а k 1 , k 2 {\displaystyle {k_{1}},{k_{2}}} принимают значения 0 или 1.

Средневековая математика почти никак не продвинулась в этом вопросе. Лишь в 1796 году Карлу Фридриху Гауссу удалось доказать, что если число сторон правильного многоугольника равно простому числу Ферма, то его можно построить при помощи циркуля и линейки. На сегодняшний день известны следующие простые числа Ферма: 3, 5, 17, 257, 65537. Вопрос о наличии или отсутствии других таких чисел остаётся открытым.

Точку в деле построения правильных многоугольников поставило нахождение построений 17-, 257- и 65537-угольника. Первое было найдено Йоханнесом Эрхингером в 1825 году, второе — Фридрихом Юлиусом Ришело в 1832 году, а последнее — Иоганном Густавом Гермесом в 1894 году.

С тех пор проблема считается полностью решённой.

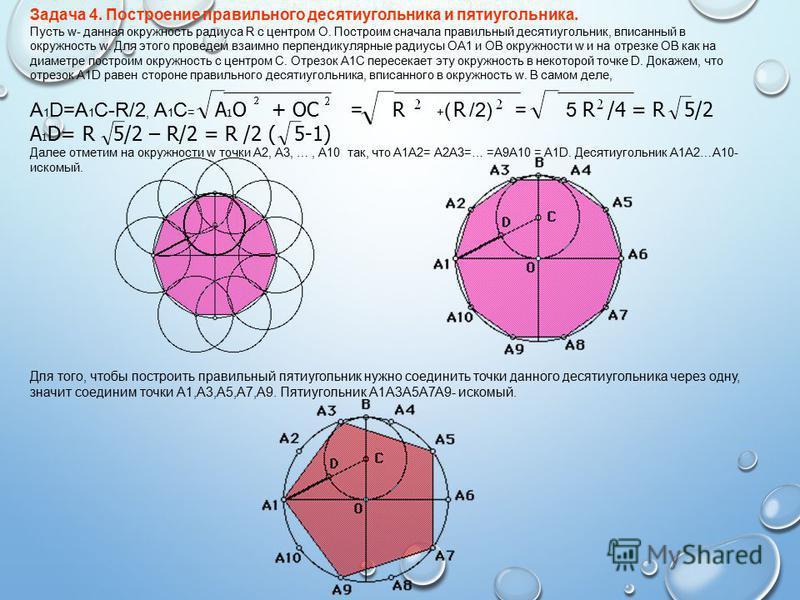
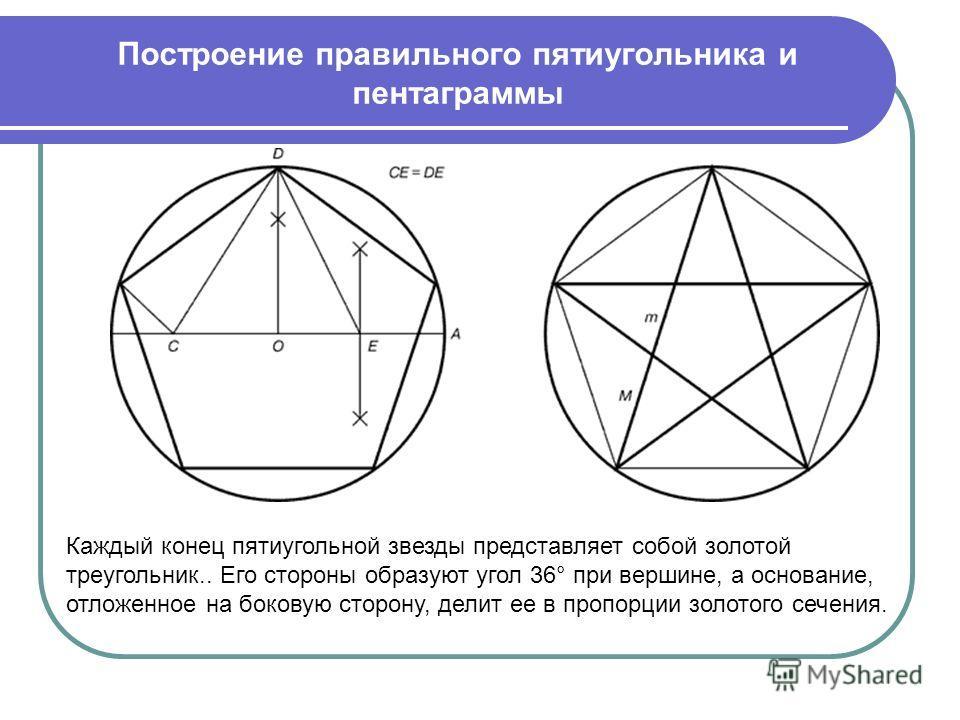
Пя­ти­у­голь­ник - это многоугольник с пятью углами. Также пятиугольником называют всякий предмет такой формы.

Пентагра́мма - фигура, полученная соединением вершин правильного пятиугольника через одну; фигура, образованна совокупностью всех диагоналей правильного пятиугольника.

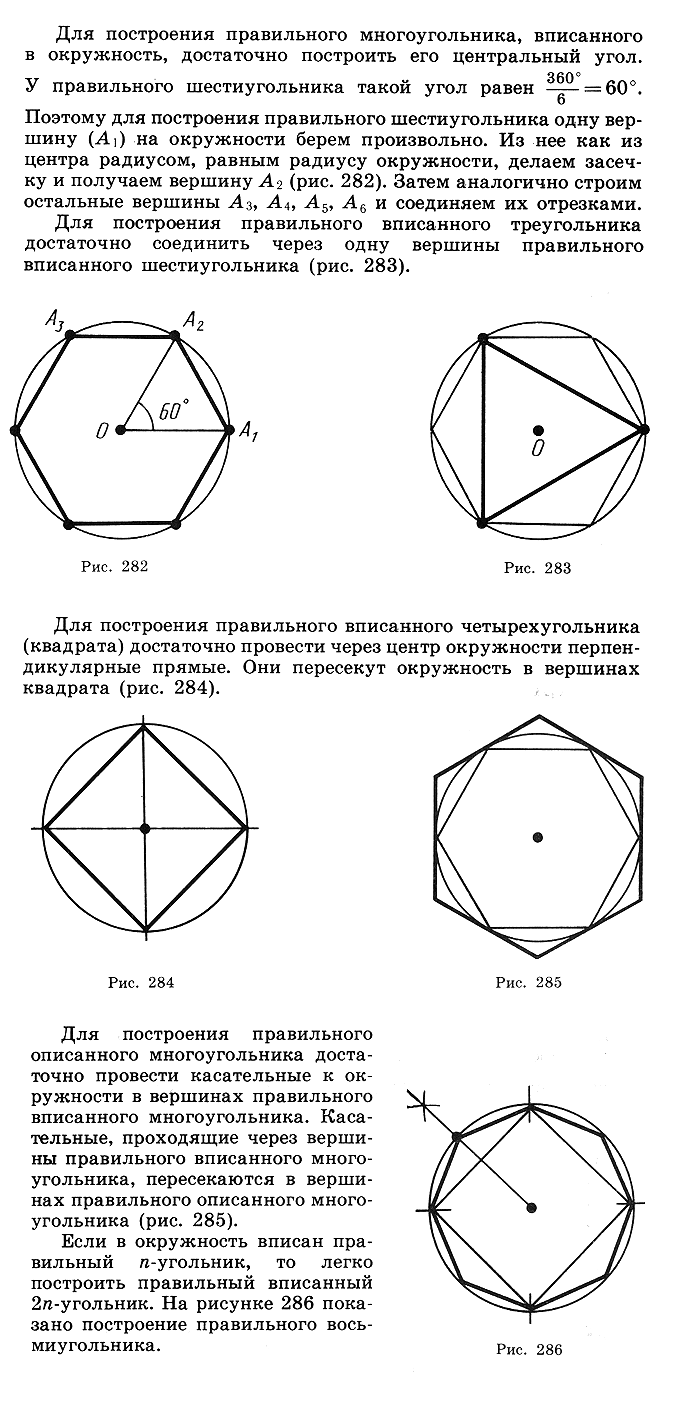
Шестиугольник - многоугольник с шестью углами. Также шестиугольником называют всякий предмет такой формы.

Гексаграмма - звезда с шестью углами, которая образуется из двух наложенных друг на друга равносторонних треугольников.

Правильный восьмиугольник (октагон)

геометрическая фигура из группы правильных многоугольников. У него восемь сторон и восемь углов, все углы и стороны равны между собой.

Семиуго́льник

называемый иногда гептагон многоугольник с семью углами. Семиугольником также называют всякий предмет такой формы.

Гептаграмма

(от греч. Hepta – “семь” и Gramma – “черта”) семиконечная фигура (звезда), магический знак семерицы.

Октаграмма

восьмилучевая звезда, крестострел.

Девятиуго́льник

многоугольник с девятью углами. Девятиугольником также называют всякий предмет, имеющий такую форму.

Заключение.

В ходе выполнения проекта я

1. Изучил литературу по данной теме.

2. Отобрал материал для выполнения проекта.

3. Познакомился видами правильных многоугольников.

4.Изучил способы построения некоторых правильных многоугольников.

5. Подготовил презентацию для защиты проекта.

Список литературы: