| № п/п | Тема | Кол-во часов | Формы и методы обучения | Основное содержание | Требование к уровню подготовки (знать/уметь)
| Оборудование, оснащение | Календарно - учебный график |
| 1. | Дроби и проценты. Прямая и обратная пропорциональность | 1ч | Словесные, наглядные, практические | Дроби, основные свойства дроби. Проценты, основные задачи на проценты: Прямо пропорциональные величины | Знать определение дроби, процента. понятие прямой и обратной пропорциональной зависимости. Уметь находить прямую и обратную пропорциональность, решение задач на проценты | Интерактивная доска, проектор | 2неделя сентября |
| 2 | Преобразование буквенных выражений (раскрытие скобок, приведение подобных слагаемых) | 1ч | Словесные, наглядные, практические | Переместительное, сочетательное и распределительное свойство умножения. Раскрытие скобок, перед которыми стоит знак «+», раскрытие скобок, перед которыми стоит знак «-» Подобные слагаемые. Приведение подобных слагаемых
| Знать: правила раскрытия скобок, приведение подобных слагаемых Уметь: применять правило раскрытия скобок при упрощении выражений, нахождении значений выражений и решении уравнений | Интерактивная доска, проектор, карточки с заданиями | 3 сентября неделя |
| 3 | Решение уравнения | 1ч | Словесные, наглядные, практические | Уравнение. Корень уравнения. Правила переноса слагаемых из одной части уравнения в другую; умножения (деления) обеих частей уравнения на одно и то же число, не равное нулю. Линейные уравнения | Знать: определения уравнения, корня уравнения, линейного уравнения, правило переноса слагаемых из одной части уравнения в другую, правило умножения (деления) обеих частей уравнения на одно и то же число, не равное нулю. Уметь: применять изученные определения и правила при решении уравнений и текстовых задач | Интерактивная доска, проектор, карточки с заданиями | 4 неделя сентября
|
| 4 | Координаты и графики. Построение графика линейной функции. | 1ч | Словесные, наглядные, практические | Функция, описывающая прямую пропорциональную зависимости, её графики; характеристика графика через угловые коэффициенты | Знать определения функции Уметь строить график линейной функции, определять координаты точек, принадлежащие графику и не принадлежащие ему | Интерактивная доска, проектор | 5 неделя сентября |
| 5 | Свойства степени с натуральным показателем | 1ч | Словесные, наглядные, практические | Определение степени с натуральным показателем, основание степени, показатель степени | Знать определения: степени с натуральным показателем, основания степени, показателя степени. Уметьнаходить значения функций, заданных формулой, таблицей, графиком; решать обратную задачу | Интерактивная доска, проектор | 2 неделя октября |
| 6. | Многочлены. Действия с многочленами. Формулы сокращенного умножения. | 1ч | Словесные, наглядные, практические | Понятие многочлена. Стандартный вид многочлена. Алгоритм приведения многочлена к стандартному виду | Знать определение одночлена; алгоритм приведения многочлена к стандартному виду. Уметь указывать коэффициент и буквенную часть многочлена, приводить одночлен к стандартному виду | Интерактивная доска, проектор, карточки с заданиями | 3 неделя октября |
| 7. | Разложения многочленов на множители | 1ч | Словесные, наглядные, практические | Понятие многочлена. Стандартный вид многочлена. Алгоритм приведения многочлена к стандартному виду.
| Знать определение многочлена, формулы сокращенного умножения Уметь выносить общий множитель за скобки, способ группировки, формулы сокращенного умножения | Интерактивная доска, проектор | 4 неделя октября |
| 8. | Основное свойство дроби | 1ч | Словесные, наглядные, практические | Основное свойство дроби, тождество, сокращение дробей. | Знать основное свойство дроби, термины «выражение», «тождественное преобразование», правило сокращение дробей. Уметь сокращать дробь. | Интерактивная доска, проектор карточки с заданиями, | 5 неделя октября
|
| 9. | Сложение и вычитание алгебраических дробей | 1ч | Словесные, наглядные, практические | Правила сложения и вычитания дробей с одинаковым знаменателем | Знать правила сложения и вычитания дробей с одинаковым знаменателем. Уметь выполнять сложение и вычитание дробей с одинаковыми знаменателями | Интерактивная доска, проектор | 2 неделя ноября |
| 10. | Умножение и деление алгебраических дробей | 1ч | Словесные, наглядные, практические | Правило умножения рациональных дробей | Знать правило умножения рациональных дробей. Уметь применять правило умножения рациональных дробей | Интерактивная доска, проектор, карточки с заданиями | 3 неделя ноября |
| 11. | Свойства степени с целым показателем | 1ч | Словесные, наглядные, практические | Свойства степени с целым показателем. Стандартный вид числа. | Знать определение, свойства степени с целым показателем Уметь выполнять действия возведения в степень произведения со степенями с натуральным показателем | Интерактивная доска, проектор, карточки с заданиями | 4 неделя ноября |
| 12. | Решение задач с помощью уравнений  
| 1ч | Словесные, наглядные, практические | Решение задач с помощью уравнений | Уметь решать задачи с помощью уравнений | Интерактивная доска, проектор | 5 неделя ноября |
| 13 | Иррациональные числа | 1ч | Словесные, наглядные, практические | Иррациональные числа | Знать определение иррационального числа Уметь определять иррациональные числа | Интерактивная доска, проектор | 2 неделя декабря |
| 14,15. | Теорема Пифагора | 2ч | Словесные, наглядные, практические | Теорема Пифагора и теорема ей обратная | Знать: формулировку теоремы Пифагора и основные этапы её доказательства и формулировку обратной ей теоремы. Уметь: находить стороны треугольника, используя теорему Пифагора; Доказывать обратную теорему и применять её при решении задач.
| Интерактивная доска, проектор, карточки с заданиями | 3,4 неделя декабря |
| 16. | Квадратный корень (алгебраический подход) | 1ч | Словесные, наглядные, практические | Функция y=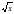 и её график и её график | Знать график функции y=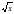 Уметь строить график функции 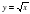 и находить значения этой функции по графику или по формуле и находить значения этой функции по графику или по формуле | Интерактивная доска, проектор | 5 неделя декабря |
| 17,18 | Преобразование выражений, содержащих квадратные корни | 2ч | Словесные, наглядные, практические | Приведенное квадратное уравнение; формулы дискриминанта и корней квадратного уравнения. | Знать определение приведённого квадратного уравнения; формулы дискриминанта и корней квадратного уравнения. Уметь решать квадратные уравнения выделением квадрата двучлена; решать квадратные уравнения по формуле. | Интерактивная доска, проектор, карточки с заданиями | 3,4 неделя января |
| 19,20 | Формулы корней квадратного уравнения | 2ч | Словесные, наглядные, практические | Формула корней квадратного уравнения | Знать определение квадратного уравнения Уметь решать квадратные уравнения, дробные рациональные уравнения. Уметь применять квадратные уравнения | Интерактивная доска, проектор, карточки с заданиями | 5 неделя января 1 неделя февраля |
| 21,22 | Теорема Виета | 2ч | Словесные, наглядные, практические | Теорема Виета. Разложение квадратного трехчлена на множители | Знать теорему Виета Уметь разкладывать квадратный трехчлен на множители | Интерактивная доска, проектор, карточки с заданиями | 2,3 неделя февраля |
| 23. | Линейное уравнение с двумя переменными и его график | 1ч | Словесные, наглядные, практические | Линейное уравнение с двумя переменными и его график | Уметь находить область определения и область значения функции. Уметь выполнять комбинированные упражнения на нахождение области определения и области значения функции | Интерактивная доска, проектор, карточки с заданиями | 4 неделя февраля |
| 24. | Уравнение прямой вида у=кх+1 | 1ч | Словесные, наглядные, практические | Уравнение прямой вида у=кх+1. | Знать определения уравнение прямой вида у=кх+1. Уметь решать, строить уравнение прямой вида у=кх+1 | Интерактивная доска, проектор, карточки с заданиями | 5 неделя февраля |
| 25. | Системы уравнений. Решение систем способом сложения
| 1ч | Словесные, наглядные, практические | Системы уравнение. Решение систем способом сложения | Уметь решать системы линейных уравнений способом сложения | Интерактивная доска, проектор, карточки с заданиями | 2 неделя марта |
| 26,27 | Системы уравнений. Решение систем способом подстановки | 2ч | Словесные, наглядные, практические | Решение систем уравнений способом подстановки | Уметь решать системы линейных уравнений способом подстановки | Интерактивная доска, проектор, карточки с заданиями | 3,4 неделя марта |
| 28,29 | Решение задач с помощью систем уравнений | 2ч | Словесные, наглядные, практические | Решение задач с помощью систем уравнений. | Уметь решение задач с помощью систем уравнений | Интерактивная доска, проектор, карточки с заданиями | 2,3 неделя апреля |
| 30. | График функции | 1ч | Словесные, наглядные, практические | График функции | Уметь распозновать, строить график функции | Интерактивная доска, проектор, карточки с заданиями | 4 неделя апреля |
| 31. | Свойства функций | 1ч | Словесные, наглядные, практические | Свойства функций | Знать свойства функции Уметь использовать свойства функции в решении задач | Интерактивная доска, проектор, карточки с заданиями | 5 неделя апреля |
| 32,33 | Линейная функция | 1ч | Словесные, наглядные, практические | Взаимное расположение графиков линейных функций, геометрический смысл коэффициентов | Знать что такое линейная функция, ее график, геометрический смысл коэффициентов Уметь строить график линейной функции | Интерактивная доска, проектор, карточки с заданиями | 1,2 неделя мая |
| 34,35 | Функция  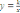 и её свойства и её свойства
| 2ч | Словесные, наглядные, практические | Обратная пропорциональность, гипербола | Знать свойства обратной пропорциональности. Уметь строить график обратной пропорциональности, находить значения 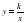 по графику, по формуле. по графику, по формуле.
| Интерактивная доска, проектор, карточки с заданиями | 3,4 неделя мая |
|
| Итого | 35ч |
|
|
|
|
|








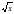 и её график
и её график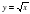 и находить значения этой функции по графику или по формуле
и находить значения этой функции по графику или по формуле
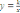
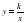 по графику, по формуле
по графику, по формуле









