
Пояснительная записка
Модифицированная дополнительная общеобразовательная общеразвивающая программа «Математика для всех» разработана в соответствии с Федеральным законом от 29. 12. 2012 года № 273 – ФЗ «Об образовании в Российской Федерации», Приказом Министерства просвещения РФ от 09.11.2018 № 196 «Об утверждении Порядка организации и осуществления образовательной деятельности по дополнительным общеобразовательным программам», СанПин 2. 4. 4. 3172 – 14 от 20. 08. 2014 г; Уставом МБОУ «Дроздовская ООШ».
Направленность программы – естественнонаучная.
Математика – удобный, даже универсальный, инструмент описания мира. А прикладная математика, то есть математика практическая, ориентированная на конкретные актуальные цели и нужды, является не только средством познания, но также и средством воздействия на окружающий мир.
Математическое образование должно подчиняться общей цели: обеспечить усвоение системы математических умений и знаний, развивать логическое мышление и пространственное воображение, сформировать представление о прикладных возможностях математики, сообщить сведения об истории развития науки, выявлять образовательные склонности и предпочтения учащихся.
Программа кружка рассчитана на учащихся, склонных к занятиям математикой и желающих повысить свой математический уровень. Именно в этом возрасте формируются математические способности и устойчивый интерес к математике.
Занятия проходят в форме беседы с опорой на индивидуальные способности учащихся. В ходе занятий предполагается обязательное выполнение практических заданий. Акцент сделан на самостоятельную работу учащихся, большое внимание уделяется индивидуальной работе.
Вопросы, рассматриваемые в курсе, выходят за рамки школьной программы, но вместе с тем тесно примыкают к ней.
Актуальность программы
Актуальность данного курса определяется тем, что учащиеся расширяют представления о математике, об исторических корнях математических понятий и символов, о роли математики в общечеловеческой культуре.
Современный этап развития общества характеризуется резким подъемом его информационной культуры, модернизацией общего образования, поэтому приоритет отдается вкладу математического образования в индивидуальное развитие личности. Развитие, прежде всего, в таких направлениях, как точность и ясность мысли, высокий уровень интеллекта, воля и целеустремленность в поисках и принятии решений, способность ориентироваться в новых ситуациях, стремление к применению полученных знаний, умение и желание постоянно учиться, творческая активность и самостоятельность.
Освоение содержания программы способствует интеллектуальному, творческому, эмоциональному развитию учащихся. При реализации содержания программы учитываются возрастные и индивидуальные возможности, личностно-деятельный подход. Уровень сложности подобранных заданий таков, что к их рассмотрению можно привлечь значительное число учащихся.
Новизна программы состоит в том, что данная программа достаточно универсальна, имеет большую практическую значимость. Она доступна обучающимся. Начинать изучение программы можно с любой темы; каждая из них имеет развивающую направленность, а также предусматривает дифференциацию по уровню подготовки обучающихся.
Педагогическая целесообразность программы
заключаются в том, что данная программа достаточно универсальна, имеет большую практическую значимость. Предлагаемая программа рассчитана на тех, кто стремится проявить и развить свои природные способности к точным дисциплинам. Так как содержание образования является одним из факторов экономического и социального прогресса общества, и ориентировано на обеспечение самоопределения личности, создание условий для ее самореализации, формирование у обучающегося адекватной современному уровню знаний и уровню образовательной программы картины мира, интеграцию личности в национальную и мировую культуру, формирование человека и гражданина, интегрированного в современное ему общество и нацеленного на совершенствование этого общества, то при разработке программы учитывались основные принципы, которым должно было соответствовать содержание программы:
- быть близким к учебной программе предмета, но обязательно новым, в какой-то степени углубляющим какой-то раздел программы;
- представлять собой системы последовательных проблем;
- быть практически интересным, связанным с жизнью, учитывать желания учащихся;
- иметь занимательную сторону, включая эстетическую.
Адресат программы
Программа рассчитана для среднего школьного возраста (12 - 15 лет). Программа доступна для детей, проявивших выдающиеся способности (одаренные), детей с ограниченными возможностями здоровья, детей, находящиеся в трудной жизненной ситуации.
Срок освоения программы
Продолжительность обучения 1 год. Форма обучения – очная.
Объем программы
Годовая нагрузка - 34 часа.
Режим занятий
Учебная программа предусматривает проведение занятий в классе 1 раз в неделю, продолжительность занятий 1 учебный час.
Учебная группа – 4 учащихся.
Форма организации ученого процесса
фронтальная;
групповая, коллективная;
индивидуальная;
комбинированная.
Формы проведения занятий:
лекции;
соревнования;
самостоятельная работа;
практическая работа.
Цель программы:
- развитие интереса к математическому творчеству, расширение математического кругозора и эрудиции обучающихся.
Задачи:
образовательные:
научить учащихся выполнять тождественные преобразования выражений;
научить учащихся основным приемам решения уравнений, неравенств и их систем;
научить строить графики и читать их;
научить различным приемам решения текстовых задач;
помочь овладеть рядом технических и интеллектуальных умений на уровне свободного их использования;
подготовить обучающихся к изучению математики в старшей школе или к поступлению в средние учебные заведения, а также к углубленному изучению математики в профильной школе.
развивающие:
повышать интерес к математике;
развивать мышление через усвоение таких приемов мыслительной деятельности как умение анализировать, сравнивать, синтезировать, обобщать, выделять главное, доказывать, опровергать;
формировать мировоззрение учащихся, логическую и эвристическую составляющие мышления, алгоритмическое мышление через работу над решением задач;
развивать пространственное воображение через решение геометрических задач;
формировать умения строить математические модели реальных явлений, анализировать построенные модели, исследовать явления по заданным моделям, применять математические методы к анализу процессов и прогнозированию их протекания через работу над проектами.
воспитательные:
воспитывать активность, самостоятельность, ответственность, трудолюбие;
воспитывать эстетическую, графическую культуру, культуру речи через подготовку и проведение недели математики, подготовку и представление докладов, решение задач;
формировать систему нравственных межличностных отношений, культуру общения, умение работы в группах через работу над проектами и работу на занятиях кружка, стремиться к формированию взаимопонимания и эффективного взаимодействия всех участников образовательного процесса, содействуя открытому и свободному обмену информацией, знаниями, а также эмоциями и чувствами через организацию качественного коммуникативного пространства на занятиях кружка.
Планируемые результаты
Программа позволяет добиваться следующих результатов:
Личностные:
у учащихся будут сформированы:
- умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
- умение контролировать процесс и результат учебной математической деятельности;
у учащихся могут быть сформированы:
- критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
- креативность мышления, инициатива, находчивость, активность при решении задач.
Метапредметные:
Регулятивные
учащиеся научатся:
- формулировать и удерживать учебную задачу;
- планировать пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
учащиеся получат возможность научиться:
- предвидеть возможности получения конкретного результата при решении задач;
- прилагать волевые усилия и преодолевать трудности и препятствия на пути достижения целей;
познавательные
учащиеся научатся:
- осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий;
- находить в различных источниках информацию и представлять ее в понятной форме;
- создавать и преобразовывать модели и схемы для решения задач;
учащиеся получат возможность научиться:
- планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;
- выбирать наиболее рациональные и эффективные способы решения задач;
- выдвигать гипотезы при решении учебных и понимать необходимость их проверки;
коммуникативные
учащиеся научатся:
- организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками;
- взаимодействовать и находить общие способы работы, работать в группе, находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов, слушать партнера, аргументировать и отстаивать свое мнение;
- аргументировать свою позицию и координировать ее с позициями партнеров в сотрудничестве, при выработке общего решения в совместной деятельности;
учащиеся получат возможность научиться:
- продуктивно разрешать конфликты на основе учета интересов и позиций всех участников, договариваться и приходить к общему решению в совместной деятельности;
- оказывать поддержку и содействие тем, от кого зависит достижение цели в совместной деятельности.
Предметные:
учащиеся научатся:
- работать с математическим текстом, точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику, обосновывать суждения;
- выполнять арифметические преобразования, применять их для решения математических задач;
- самостоятельно приобретать и применять знания в различных ситуациях при решении практических задач;
- знать основные способы представления и анализа статистических данных; уметь решать задачи с помощью перебора возможных вариантов;
учащиеся получат возможность научиться:
- применять изученные понятия, результаты и методы при решении задач, не сводящихся к непосредственному применению известных алгоритмов.
Форма контроля
Педагогический контроль знаний, умений и навыков учащихся осуществляется в несколько этапов и предусматривает несколько форм:
- тестовый контроль, представляющий собой проверку репродуктивного уровня усвоения теоретических знаний с использованием карточек-заданий, творческая зачетная работа, викторина.
- фронтальная и индивидуальная беседа.
- выполнение дифференцированных практических заданий различных уровней сложности.
- решение ситуационных задач направленное на проверку умений использовать приобретенные знания на практике.
- участие в конкурсах и викторинам, что позволяет воспитанникам адекватно оценивать уровень своего мастерства и результаты труда.
Критерием успешной работы кружка должно служить качество математической подготовки обучающихся, подготовка к олимпиадам, умение использовать различные методы и приемы решения поставленных задач, успешная сдача экзамена за курс основной школы в форме ОГЭ.
Предметом оценивания являются:
- набор основных знаний, умений, навыков по изучаемому виду деятельности, а также общеучебных навыков, которые должен приобрести ребёнок в результате освоения материала по конкретной дополнительной общеразвивающей программе;
- важнейшие личностные свойства, которые необходимо сформировать у ребёнка за период его обучения по данной программе, и время общения с педагогом и сверстниками
Отчёт о проделанной работе позволяет научить ребёнка последовательности в работе, развивать осознанный интерес детей к творческой деятельности;
Способы определения результативности программы:
Личностными результатами изучения курса является формирование следующих умений:
- определять и высказывать под руководством педагога самые простые общие для всех людей правила поведения при сотрудничестве (этические нормы).
- в предложенных педагогом ситуациях общения и сотрудничества, опираясь на общие для всех простые правила поведения, делать выбор, при поддержке других участников группы и педагога, как поступить.
Для оценки формирования и развития личностных характеристик воспитанников (ценности, интересы, склонности, уровень притязаний положение ребенка в объединении, деловые качества воспитанника) используется
простое наблюдение,
проведение математических игр,
опросники,
анкетирование
Занятия рассчитаны на групповую и индивидуальную работу. Они построены таким образом, что один вид деятельности сменяется другим. Это позволяет сделать работу динамичной, насыщенной и менее утомительной, при этом принимать во внимание способности каждого ученика в отдельности, включая его по мере возможности в групповую работу, моделировать и воспроизводить ситуации, трудные для ученика, но возможные в обыденной жизни; их анализ и проигрывание могут стать основой для позитивных сдвигов в развитии личности ребёнка.
Самым главным результатом данной программы является развитие интеллектуальных возможностей школьников и привитие стойкого интереса к предмету математике.
Для определения качества образования и развития детей мы используем различные мероприятия для фиксации промежуточного и конечного результата:
- успехи выступления на олимпиадах (дипломы, грамоты и похвальные листы)
- итоговые зачеты по каждому году обучения (годовая олимпиада);
- награждение «Дипломами» в различных математических викторинах, боях, фестивалях и т.д.
Формы аттестации
работа по карточкам, тестирование, зачетные и контрольные работы и т. д.
Итоговая аттестация по программе является обязательной.
Итоги промежуточной аттестации подводятся в виде оценки «зачтено» / «не зачтено», «освоил»/ «не освоил». Пороговое значение: 50% правильных ответов на вопросы теста. Оценивание проводится по 2-х–балльной шкале:
- зачтено – при прохождении тестирования учащийся дал правильные ответы на 50 - 100% вопросов;
- не зачтено - при прохождении тестирования учащийся дал правильные ответы на 0 - 49% вопросов.
При недостаточном освоении материала планируются дополнительные и индивидуальные занятия.
Оценочные материалы
Примеры заданий по разделу 1.
Практическое задание №1 «Степень с целым показателем».

Практическое задание №2. «Дробно-рациональные выражения. Область допустимых значений переменной».
Задание 1. Найдите значение выражения 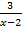 при
при 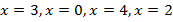 .
.
Задание 2. Определить недопустимые значения переменной  в выражении
в выражении  .
.
Задание 3. Определить недопустимые значения переменной  в выражении
в выражении 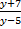 .
.
Примеры заданий по разделу 2.
Тест №1. « Квадратные корни. Арифметический квадратный корень».
1.Найдите верное равенство
а)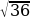 = -6 б)
= -6 б)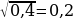 в)
в)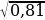 = 0,9
= 0,9
2.Найдите значение арифметического квадратного корня: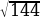
а) 12 б) 72 в)14
3. Найдите значение арифметического квадратного корня: 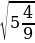
а) 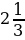 ; б)
; б) 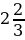 ; в)
; в)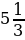
4. Найдите значение арифметического квадратного корня 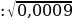
а)0,3 б) 0,03 в)0,0003
5. 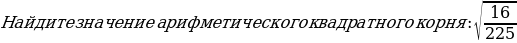
а) 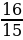 б)
б) 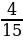 в)
в)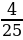
6.Найдите значение выражения: - (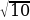 )2
)2
а) 100 б) -10 в)10
7. Найдите значение выражения: ( -4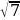 )2
)2
а) 112 б) 28 в)-28
8.Найдите значение выражения: 4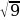 - 2
- 2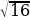
а) 16 б) 4 в)8
9.Решите уравнение: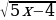 = 6
= 6
а) х=3,2 б) х=8 в) х=2
10.Решите уравнение: 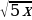 – 4 =6
– 4 =6
а) х=3,2 б) х=8 в)х=2
Примеры заданий по разделу 3.
Практическое задание №3 «Основные методы решения уравнений. Разложение на множители».
Пример 1. Решение уравнений способом вынесения общего множителя за скобки
x3 – 5x2 + 6x = 0.
Пример 2. Решение уравнений способом группировки
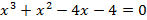
Пример 3. Решение уравнений с помощью формул сокращенного умножения
х4 = (3х-10)2
Практическое задание №4. «Основные приёмы решения систем уравнений».
Пример 1. Решить систему способом подстановки, методом сложения и графически
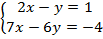
Практическое задание №5. «Метод интервалов – универсальный метод решения неравенств».
Пример 1. Решить неравенство методом интервалов: x2 - 5x + 6 ≥ 0.
Пример 2. Применить метод интервалов для решения неравенства х2+4х+3
Практическое задание №6. «Уравнения и неравенства».
1. Решите неравенство 9x−4(2x+1)− 80 .
2. Решите систему уравнений:
а) 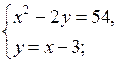
3. Изобразите на координатной плоскости множество решений системы неравенств:
а) 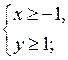
Примеры заданий по разделу 4.
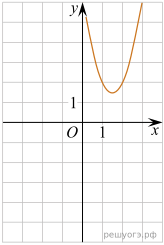
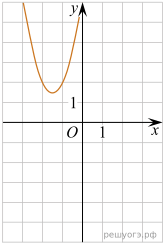
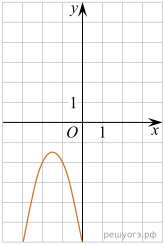
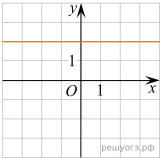
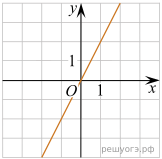
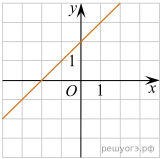
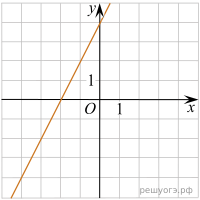
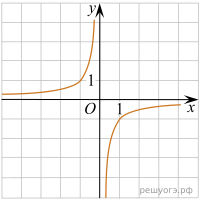
Практическое задание №7. «Установление соответствия между графиком функции и его аналитическим заданием».
1. Установите соответствие между графиками функций и формулами, которые их задают.
Графики
Формулы
2. Установите соответствие между графиками функций и формулами, которые их задают.
1) 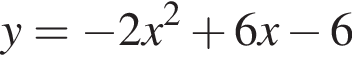
2) 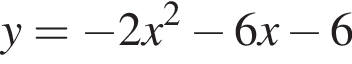
3) 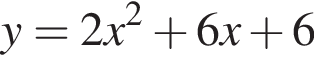
4) 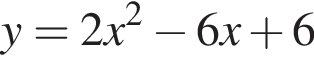
3. Установите соответствие между графиками функций и формулами, которые их задают.
1) 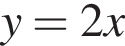
2) 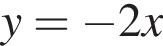
3) 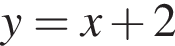
4) 
4. Установите соответствие между графиками функций и формулами, которые их задают.
1) 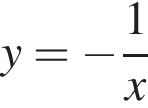
2) 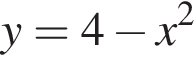
3) 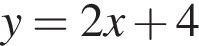
4) 
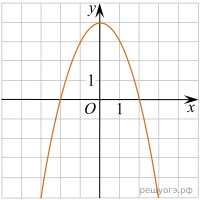
5. На рисунке изображен график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции являются верными? Запишите их номера.
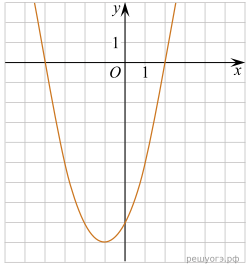
1) Функция убывает на промежутке [−1; +∞ )
2) f(x)0 при xx2
3) Наименьшее значение функции равно −9
Практическое задание №8. «Построение графиков функций, содержащих знак модуля».
Практическое задание №9. «Построение графиков кусочно заданных функций».
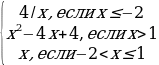
При каких значениях m прямая y=m имеет с графиком этой функции одну общую точку?
Примеры заданий по разделу 5.
Практическое задание №10. «Арифметическая прогрессия и задачи связанные с ней».
1. Бригада маляров красит забор длиной 240 метров, ежедневно увеличивая норму покраски на одно и то же число метров. Известно, что за первый и последний день в сумме бригада покрасила 60 метров забора. Определите, сколько дней бригада маляров красила весь забор.
2. Турист идет из одного города в другой, каждый день проходя больше, чем в предыдущий день, на одно и то же расстояние. Известно, что за первый день турист прошел 10 километров. Определите, сколько километров прошел турист за третий день, если весь путь он прошел за 6 дней, а расстояние между городами составляет 120 километров.
3. Тренер посоветовал Андрею в первый день занятий провести на беговой дорожке 15 минут, а на каждом следующем занятии увеличивать время, проведённое на беговой дорожке, на 7 минут. За сколько занятий Андрей проведёт на беговой дорожке в общей сложности 2 часа 25 минут, если будет следовать советам тренера?
4. Врач прописал пациенту принимать лекарство по такой схеме: в первый день он должен принять 3 капли, а в каждый следующий день — на 3 капли больше, чем в предыдущий. Приняв в день 30 капель, он ещё 3 дня пьёт по 30 капель лекарства, а потом ежедневно уменьшает приём на 3 капли. Сколько пузырьков лекарства нужно купить пациенту на весь курс приёма, если в каждом содержится 20 мл лекарства (что составляет 250 капель)?
5. Клиент взял в банке кредит 100 рублей на n месяцев с условием, что по окончании первого месяца выплатит банку  часть кредита, а в каждый последующий месяц выплата будет на 5 рублей больше, чем в предыдущий. Известно, что в последний месяц выплата составила 55 руб. На какой срок был выдан кредит, если известно, что этот срок превышал полгода?
часть кредита, а в каждый последующий месяц выплата будет на 5 рублей больше, чем в предыдущий. Известно, что в последний месяц выплата составила 55 руб. На какой срок был выдан кредит, если известно, что этот срок превышал полгода?
Практическое задание №11. «Геометрическая прогрессия и задачи связанные с ней».
1. В геометрической прогрессии 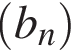 известно, что
известно, что 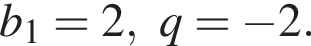 Найти пятый член этой прогрессии.
Найти пятый член этой прогрессии.
3. Дана геометрическая прогрессия (bn), знаменатель которой равен 2, а 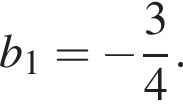 Найдите сумму первых шести ее членов.
Найдите сумму первых шести ее членов.
4. В геометрической прогрессии сумма первого и второго членов равна 75, а сумма второго и третьего членов равна 150. Найдите первые три члена этой прогрессии.
Тест №2. Решение задач по теме «Последовательности».
1. Какая из последовательностей является геометрической прогрессией?
А. Последовательность натуральных чисел кратных 3.
Б. Последовательность кубов натуральных чисел.
В. Последовательность натуральных степеней числа 3.
Г. Последовательность чисел, обратных натуральным.
2. Из арифметических прогрессий выберите ту, среди членов которой
есть число –10.
А. аn = 2n + 10 Б. аn = –3n В. аn = –3n + 2 Г. аn = –4n – 8.
3. Фигуры составляются из квадратов, как показано на рисунке. Из
какого количества квадратов составлена фигура с номером равным 100?
А. 200 Б. 201 В. 202 Г. 203
4. Последовательность задана формулой сn =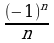 . Какое из чисел не
. Какое из чисел не
является членом этой последовательности?
А. -1 Б. 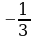 В.
В. 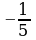 Г.
Г. 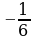
5. За первые сутки на автостоянке надо заплатить 30 р., а за каждые
последующие – на 1 р. меньше, чем за предыдущие. Автомобиль был
оставлен на стоянке на 12 суток. Сколько придётся заплатить
автовладельцу?
А. 349 р. Б. 294 р. В. 288 р. Г. 19 р.
6. В геометрической прогрессии (bn) b4 = 8, b6 = 12. Найдите b8.
Ответ: _________________
7. Найдите третий член каждой из арифметических прогрессий, если
известны их вторые и четвёртые члены. В таблице под каждой
буквой запишите номер ответа, под которым указано
соответствующее значение.
А. а2 = 12, а4 = 6 Б. b2 = -3, b4 = 7 В. c2 = 1,2, с4 = 6,8
1) 5,6 2) 2 3) 9 4) 4
Ответ:
Практическое задание №12. «Задачи на проценты».
1. На пост главы администрации города претендовало три кандидата: Журавлев, Зайцев, Иванов. Во время выборов за Иванова было отдано в 2 раза больше голосов, чем за Журавлева, а за Зайцева — в 3 раза больше, чем за Журавлева и Иванова вместе. Сколько процентов голосов было отдано за победителя?
2. При смешивании первого раствора кислоты, концентрация которого 20%, и второго раствора этой же кислоты, концентрация которого 50%, получили раствор, содержащий 30% кислоты. В каком отношении были взяты первый и второй растворы?
3. Свежие фрукты содержат 80% воды, а высушенные — 28%. Сколько сухих фруктов получится из 288 кг свежих фруктов?
Практическое задание №13. «Задачи на пропорциональные отношения».
1. На пост председателя школьного совета претендовали два кандидата. В голосовании приняли участие 120 человек. Голоса между кандидатами распределились в отношении 3:5. Сколько голосов получил победитель?
2. Тест по математике содержит 30 заданий, из которых 18 заданий по алгебре, остальные –– по геометрии. В каком отношении содержатся в тесте алгебраические и геометрические задания?
| 1) 3:2 | 2) 2:3 | 3) 3:5 | 4) 5:3 |
3. Во время выборов голоса избирателей между двумя кандидатами распределились в отношении 3:2. Сколько процентов голосов получил проигравший?
Примеры заданий по разделу 6.
Практическое задание №14. «Измерение площадей».
1. Площадь прямоугольного земельного участка равна 9 га, ширина участка равна 150 м. Найдите длину этого участка в метрах.
2. Сколько досок длиной 3,5 м, шириной 20 см и толщиной 20 мм выйдет из четырехугольной балки длиной 105 дм, имеющей в сечении прямоугольник размером 30 см  40 см?
40 см?
3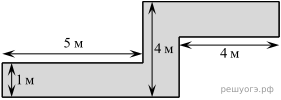 . Определите, сколько необходимо закупить пленки
. Определите, сколько необходимо закупить пленки 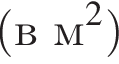 для гидроизоляции садовой дорожки, изображенной на рисунке, если ее ширина везде одинакова.
для гидроизоляции садовой дорожки, изображенной на рисунке, если ее ширина везде одинакова.
4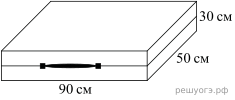 . Дизайнер Павел получил заказ на декорирование чемодана цветной бумагой. По рисунку определите, сколько бумаги (в см2) необходимо закупить Павлу, чтобы оклеить всю внешнюю поверхность чемодана, если каждую грань он будет обклеивать отдельно (без загибов).
. Дизайнер Павел получил заказ на декорирование чемодана цветной бумагой. По рисунку определите, сколько бумаги (в см2) необходимо закупить Павлу, чтобы оклеить всю внешнюю поверхность чемодана, если каждую грань он будет обклеивать отдельно (без загибов).

Практическое задание №15. «Теорема Пифагора».
1. Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний ее конец, если нижний конец отстоит от ствола дерева на 1,8 м?
2 . Мальчик прошел от дома по направлению на восток 800 м. Затем повернул на север и прошел 600 м. На каком расстоянии (в метрах) от дома оказался мальчик?
. Мальчик прошел от дома по направлению на восток 800 м. Затем повернул на север и прошел 600 м. На каком расстоянии (в метрах) от дома оказался мальчик?
3 . Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 15 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 8 м. Найдите длину троса.
. Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 15 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 8 м. Найдите длину троса.
4 . Длина стремянки в сложенном виде равна 1,85 м, а ее высота в разложенном виде составляет 1,48 м. Найдите расстояние (в метрах) между основаниями стремянки в разложенном виде.
. Длина стремянки в сложенном виде равна 1,85 м, а ее высота в разложенном виде составляет 1,48 м. Найдите расстояние (в метрах) между основаниями стремянки в разложенном виде.
Практическое задание №16. «Подобие треугольников».
1. Короткое плечо шлагбаума имеет длину 1 м, а длинное плечо – 3 м. На какую высоту (в метрах) опустится конец короткого плеча, когда конец длинного плеча поднимается на 1,8 м? 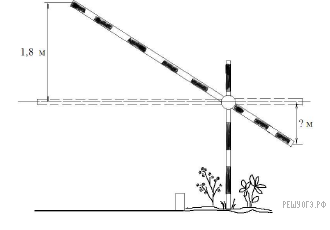
2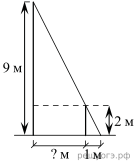 . На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?
. На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?
3. Человек, рост которого равен 1,8 м, стоит на расстоянии 16 м от уличного фонаря. При этом длина тени человека равна 9 м. Определите высоту фонаря (в метрах).

4 . Проектор полностью освещает экран A высотой 80 см, расположенный на расстоянии 120 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 330 см, чтобы он был полностью освещен, если настройки проектора остаются неизменными?
. Проектор полностью освещает экран A высотой 80 см, расположенный на расстоянии 120 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 330 см, чтобы он был полностью освещен, если настройки проектора остаются неизменными?
Примеры заданий по разделу 7.
Тест №3. Итоговое занятие.
Тест состоит из 6 заданий по алгебре, 3 заданий по геометрии и 3 заданий по разделу «Реальная математика». На выполнение теста отводится 40 минут. Тест представлен в 2-х вариантах. Тест содержит 2 задания с выбором ответа из 4-х предложенных, 2 заданий на соответствие и 8 заданий, в которых необходимо записать ответ, полученный у учащихся. К тесту даны ключи к проверке.
ОТВЕТЫ ЗАДАНИЙ
ВАРИАНТ 1 ВАРИАНТ 2
| № задания | Ответ |
| 1 | -0,575 или -23/40 |
| 2 | 2 |
| 3 | 14 |
| 4 | 431 |
| 5 | 265 |
| 6 | 231 |
| 7 | 69 |
| 8 | 7 |
| 9 | 3 |
| 10 | 2 |
| 11 | 1980 |
| 12 | 10 |
| № задания | Ответ |
| 1 | 20,75 |
| 2 | 2 |
| 3 | 0,5 |
| 4 | 432 |
| 5 | -410 |
| 6 | 312 |
| 7 | 70 |
| 8 | 0,75 или 3/4 |
| 9 | -26 |
| 10 | 1 |
| 11 | 12700 |
| 12 | 1 |
ВАРИАНТ 1
Фамилия_____________________________________
Имя ____________________________________
Отчество _____________________________________
1. Найдите значение выражения 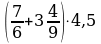
Ответ: ____________
2. Какое из чисел: 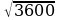 ,
,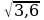 ,
, 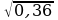 - является иррациональным?
- является иррациональным?
1) 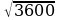 2)
2) 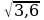 3)
3) 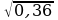 4) ни одно из этих чисел
4) ни одно из этих чисел
3. Решите уравнение: 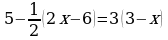
Ответ: ____________
4. Установите соответствие между графиками функций и формулами, которые их задают.
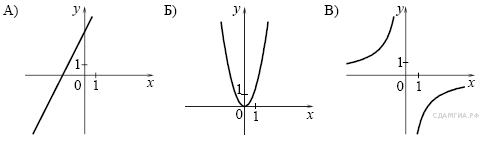
1) 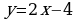 2)
2) 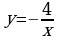 3)
3) 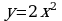 4)
4) 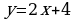
5. Арифметическая прогрессия задана первыми двумя членами:
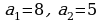 . Найдите сумму первых 20 членов этой прогрессии.
. Найдите сумму первых 20 членов этой прогрессии.
Ответ: ____________
6. Для каждого неравенства укажите множество его решений
а) 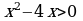 1)
1) 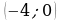
б) 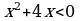 2)
2) 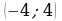
в) 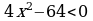 3)
3) 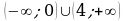
7. В треугольнике ABC внешние углы при вершинах B и C равны 105˚ и 145˚ соответственно. Найдите градусную меру угла A.
Ответ: ____________
8. В равнобедренном треугольнике ABC боковая сторона AB равна 20, основание AC равно 32. Найдите 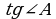 .
.
Ответ: ____________
9. Вектор 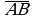 с началом в точке
с началом в точке 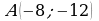 имеет координаты
имеет координаты 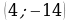 . Найдите ординату точки B.
. Найдите ординату точки B.
Ответ: ____________
10. В таблице приведены нормативы по прыжкам в длину для учащихся девятых классов. Оцените результат девочки, прыгнувшей в длину 3,85 м.
|
| Мальчики | Девочки |
| отметка | «5» | «4» | «3» | «5» | «4» | «3» |
| Длина, см | 430 | 380 | 330 | 370 | 330 | 290 |
1) отметка «5» 3) отметка «3»
2) отметка «4» 4) норматив не выполнен
11. Билет в театр стоит 500 рублей. Школьникам предоставляется скидка в размере 30% от полной стоимости билета. Сколько рублей нужно заплатить за билеты на группу, состоящую из 32 школьников и 3 учителей.
Ответ: ____________
12. Записан рост (в сантиметрах) шести учащихся: 152, 158, 137, 130, 134, 147. На сколько отличается среднее арифметическое этого набора чисел от его медианы?
Ответ: ____________
ВАРИАНТ 2
Фамилия_____________________________________
Имя ____________________________________
Отчество _____________________________________
1. Найдите значение выражения 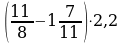
Ответ: ____________
2. Какое из чисел: 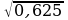 ,
,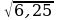 ,
, 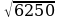 - является рациональным?
- является рациональным?
1) 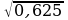 2)
2) 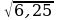 3)
3) 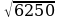 4) ни одно из этих чисел
4) ни одно из этих чисел
3. Решите уравнение: 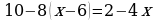
Ответ: ____________
4. Установите соответствие между графиками функций и формулами, которые их задают.
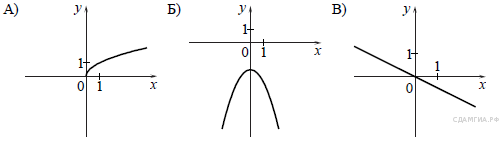
1) 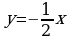 2)
2) 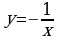 3)
3) 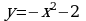 4)
4) 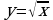
5. Арифметическая прогрессия задана первыми двумя членами: 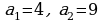 . Найдите сумму первых 10 членов этой прогрессии.
. Найдите сумму первых 10 членов этой прогрессии.
Ответ: ____________
6. Для каждого неравенства укажите множество его решений
а) 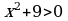 1)
1) 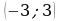
б) 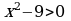 2)
2) 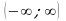
в) 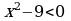 3)
3) 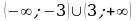
7. В треугольнике ABC угол A равен 46˚, внешний угол при вершине B равен 115˚. Найдите градусную меру угла C.
Ответ: ____________
8. В равнобедренном треугольнике ABC с основанием AC боковая сторона AB равна 14, а 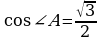 . Найдите высоту, проведенную к основанию.
. Найдите высоту, проведенную к основанию.
Ответ: ____________
9. Вектор 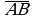 с началом в точке
с началом в точке 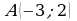 имеет координаты
имеет координаты 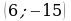 . Найдите абсциссу точки B.
. Найдите абсциссу точки B.
Ответ: ____________
10. В таблице приведены нормативы по бегу на дистанцию 60 метров для учащихся девятых классов. Оцените результат мальчика, пробежавшего 60 метров за 9,1 секунды.
|
| Мальчики | Девочки |
| отметка | «5» | «4» | «3» | «5» | «4» | «3» |
| Время, сек | 8,4 | 9,2 | 10,0 | 9,4 | 10,0 | 10,5 |
1) отметка «5» 3) отметка «3»
2) отметка «4» 4) норматив не выполнен
11. Билет в музей стоит 150 рублей. Стоимость билета для школьника составляет 40% от полной стоимости билета. Сколько рублей нужно заплатить за билеты на группу, состоящую из 28 школьников и 2 учителей.
Ответ: ____________
12. Записан рост (в сантиметрах) пяти учащихся: 158, 166, 134, 130, 132.
На сколько отличается среднее арифметическое этого набора чисел от его медианы?
Ответ: ____________
Условия реализации программы
Учебно-методическое обеспечение и техническое оснащение
Для организации качественных занятий необходимо:
- наличие светлого просторного помещения,
- мультимедийная техника и компьютер (для демонстрации презентаций)
Материально-техническое обеспечение:
- кабинет;
- доска, мел;
- ноутбук;
- таблицы с теоретическими материалами;
- раздаточный материал.
Учебный (тематический) план
Учебный (тематический) план программы представлен в таблице 1.
Таблица 1.
| №№ п/п | Наименование разделов | Количество часов | Формы контроля, аттестация |
| Всего | Теория | Практика |
| 1 1. | Тождественные преобразования. Степень с целым показателем | 3 | 1 | 2 | Беседа, практическое задание |
| 22. | Числа. Делимость натуральных чисел. Квадратные корни
| 2 | 1 | 1 | Беседа, тестирование |
| 33. | Решение уравнений и неравенств | 9 | 5 | 4 | Беседа, практическое задание, тестирование |
| 4 4. | Функции | 6 | 3 | 3 | Беседа, практическое задание |
| 55. | Последовательности и прогрессии. Решение текстовых задач
| 8 | 3 | 5 | Беседа, практическое задание |
| 6 6. | Геометрические задачи с практическим содержанием
| 5 | 2 | 3 | Беседа, практическое задание |
| 77. | Итоговое занятие
| 1 | 0 | 1 | Тестирование |
|
| Всего | 34 | 15 | 19 |
|
Содержание учебного плана
1. Тождественные преобразования. Степень с целым показателем (3 ч)
Теория: Степень с целым показателем. Вычисление значения алгебраического выражения при заданных значениях переменных. Дробно-рациональные выражения. Область допустимых значений переменной.
Практика: закрепить знания и умения по выполнению действий с алгебраическими дробями. Ввести понятие степени с целым показателем, научить применять ее при вычислениях и преобразованиях. Решение нестандартных задач по данной теме.
2. Числа. Делимость натуральных чисел. Квадратные корни (2 ч)
Теория: Развитие понятия о числе. Иррациональные числа. Действительные числа. Арифметический квадратный корень. Корень третьей степени. Делимость натуральных чисел.
Практика: обобщить и систематизировать знания учащихся по теме «Делимость натуральных чисел», закрепить теоретические знания: определения делитель, кратное, простые и составные числа, свойства и признаки делимости, алгоритмы нахождения НОД и НОК, сформировать умения применять полученные теоретические знания для решения задач, выработать у учащихся практические навыки при работе с корнями квадратными. Продолжать формировать умения решать нестандартные задачи.
3. Решение уравнений и неравенств (9 ч)
Теория: Равносильность уравнений и систем уравнений. Квадратный трёхчлен. Теорема Виета. Основные методы решения уравнений. Разложение на множители. Введение новой переменной. Основные приёмы решения систем уравнений. Равносильность неравенств. Свойства неравенств. Метод интервалов – универсальный метод решения неравенств. Методы решения систем неравенств. Итоговое занятие по теме «Уравнения и неравенства».
Практика: обеспечить овладение учащимися умением решать квадратные уравнения различными способами, выработать практические умения по данному вопросу. Выработать умения решать квадратные неравенства методом интервалов. Иметь представление об иррациональных уравнениях.
4. Функции (6 ч)
Теория: Уравнения прямой, параболы и гиперболы. Геометрический смысл коэффициентов уравнения. Установление соответствия между графиком функции и его аналитическим заданием. Чтение графиков функций. Элементарные приёмы построения и преобразования графиков функций. Построение графиков функций, содержащих знак модуля. Построение графиков кусочно заданных функций.
Практика: выработать прочные навыки по работе с графиками функций.
5. Последовательности и прогрессии. Решение текстовых задач (8 ч)
Теория: Числовые последовательности и способы их задания. Самые известные числовые последовательности. Арифметическая прогрессия и задачи связанные с ней. Геометрическая прогрессия и задачи связанные с ней. Решение задач по теме «Последовательности». Алгоритм моделирования практических ситуаций. Основные типы текстовых задач. Задачи на движение. Задачи на совместную работу. Задачи на проценты. Задачи на пропорциональные отношения.
Практика: закрепить приёмы решения практических задач с применением формул арифметической и геометрической прогрессий.
6. Геометрические задачи с практическим содержанием (5 ч)
Теория: Многоугольники. Окружность, круг. Измерение площадей. Теорема Пифагора. Подобие треугольников.
Практика: познакомить обучающихся с видами четырехугольников, разобрать их свойства и признаки. Знать возможные случаи взаимного расположения прямой и окружности, определение касательной, свойство и признак касательной. Уметь их доказывать и применять при решении задач; выполнять задачи на построение окружностей и касательных, определять отрезки хорд окружностей. Ввести понятие площади четырехугольника, решать задачи, развивать логическое мышление, разъяснить понятие теоремы и ее доказательство, выработать умение применять при решении задач признаки равенства треугольников и свойства равнобедренных треугольников. Изучить признаки подобия треугольников, продолжать решать задачи по изученной теме.
7. Итоговое занятие (1 ч)
Тестирование.
Календарный учебный график представлен в таблице 2.
Таблица 2.
| № п/п | Месяц | Число | Время проведения занятия | Форма занятия | Кол-во часов | Тема занятия | Место проведения | Форма контроля |
| 1 |
|
| 14.20 -15.00 | Практическая работа | 1 | Степень с целым показателем. | МБОУ «Дроздовская ООШ» | Практическое задание |
| 2 |
|
| 14.20 -15.00 | Практическая работа | 1 | Вычисление значения алгебраического выражения при заданных значениях переменных. | МБОУ «Дроздовская ООШ» | Беседа |
| 3 |
|
| 14.20 -15.00 | Лекция | 1 | Дробно- рациональные выражения. Область допустимых значений переменной.
| МБОУ «Дроздовская ООШ» | Практическое задание |
| 4 |
|
| 14.20 -15.00 | Лекция | 1 | Делимость натуральных чисел. | МБОУ «Дроздовская ООШ» | Беседа |
| 5 |
|
| 14.20 -15.00 | Практическая работа | 1 | Развитие понятия о числе. Иррациональные числа. Действительные числа. Арифметический квадратный корень. Корень третьей степени. | МБОУ «Дроздовская ООШ» | Тестирование |
| 6 |
|
| 14.20 -15.00 | Лекция | 1 | Равносильность уравнений и систем уравнений. | МБОУ «Дроздовская ООШ» | Беседа |
| 7 |
|
| 14.20 -15.00 | Лекция | 1 | Квадратный трёхчлен. Теорема Виета.
| МБОУ «Дроздовская ООШ» | Беседа |
| 8 |
|
| 14.20 -15.00 | Практическая работа | 1 | Основные методы решения уравнений. Разложение на множители. | МБОУ «Дроздовская ООШ» | Практическое задание |
| 9 |
|
| 14.20 -15.00 | Лекция | 1 | Введение новой переменной. | МБОУ «Дроздовская ООШ» | Беседа |
| 10 |
|
| 14.20 -15.00 | Практическая работа | 1 | Основные приёмы решения систем уравнений. | МБОУ «Дроздовская ООШ» | Практическое задание |
| 11 |
|
| 14.20 -15.00 | Лекция | 1 | Равносильность неравенств. Свойства неравенств. | МБОУ «Дроздовская ООШ» | Беседа |
| 12 |
|
| 14.20 -15.00 | Практическая работа | 1 | Метод интервалов – универсальный метод решения неравенств.
| МБОУ «Дроздовская ООШ» | Практическое задание |
| 13 |
|
| 14.20 -15.00 | Лекция | 1 | Методы решения систем неравенств. | МБОУ «Дроздовская ООШ» | Беседа |
| 14 |
|
| 14.20 -15.00 | Самостоятельная работа | 1 | Итоговое занятие по теме «Уравнения и неравенства». | МБОУ «Дроздовская ООШ» | Практическое задание. |
| 15 |
|
| 14.20 -15.00 | Лекция | 1 | Уравнения прямой, параболы и гиперболы. Геометрический смысл коэффициентов уравнения.
| МБОУ «Дроздовская ООШ» | Беседа |
| 16 |
|
| 14.20 -15.00 | Практическая работа | 1 | Установление соответствия между графиком функции и его аналитическим заданием. | МБОУ «Дроздовская ООШ» | Практическое задание |
| 17 |
|
| 14.20 -15.00 | Лекция | 1 | Чтение графиков функций. | МБОУ «Дроздовская ООШ» | Беседа |
| 18 |
|
| 14.20 -15.00 | Лекция | 1 | Элементарные приёмы построения и преобразования графиков функций. | МБОУ «Дроздовская ООШ» | Беседа |
| 19 |
|
| 14.20 -15.00 | Практическая работа | 1 | Построение графиков функций, содержащих знак модуля. | МБОУ «Дроздовская ООШ» | Практическое задание |
| 20 |
|
| 14.20 -15.00 | Практическая работа | 1 | Построение графиков кусочно заданных функций. | МБОУ «Дроздовская ООШ» | Практическое задание |
| 21 |
|
| 14.20 -15.00 | Лекция | 1 | Числовые последовательности и способы их задания. Самые известные числовые последовательности. | МБОУ «Дроздовская ООШ» | Беседа |
| 22 |
|
| 14.20 -15.00 | Практическая работа | 1 | Арифметическая прогрессия и задачи связанные с ней. | МБОУ «Дроздовская ООШ» | Практическое задание |
| 23 |
|
| 14.20 -15.00 | Практическая работа | 1 | Геометрическая прогрессия и задачи связанные с ней. | МКОУ «Дроздовская ООШ» | Практическое задание |
| 24 |
|
| 14.20 -15.00 | Самостоятельная работа | 1 | Решение задач по теме «Последовательности».
| МБОУ «Дроздовская ООШ» | Тестирование |
| 25 |
|
| 14.20 -15.00 | Лекция | 1 | Алгоритм моделирования практических ситуаций. Основные типы текстовых задач. Задачи на движение. | МБОУ «Дроздовская ООШ» | Беседа |
| 26 |
|
| 14.20 -15.00 | Лекция | 1 | Задачи на совместную работу. | МБОУ «Дроздовская ООШ» | Беседа |
| 27 |
|
| 14.20 -15.00 | Практическая работа | 1 | Задачи на проценты. | МБОУ «Дроздовская ООШ» | Практическое задание |
| 28 |
|
| 14.20 -15.00 | Практическая работа | 1 | Задачи на пропорциональные отношения. | МБОУ «Дроздовская ООШ» | Практическое задание |
| 29 |
|
| 14.20 -15.00 | Лекция | 1 | Многоугольники.
| МБОУ «Дроздовская ООШ» | Беседа |
| 30 |
|
| 14.20 -15.00 | Лекция | 1 | Окружность, круг. | МБОУ «Дроздовская ООШ» | Беседа |
| 31 |
|
| 14.20 -15.00 | Практическая работа | 1 | Измерение площадей. | МБОУ «Дроздовская ООШ» | Практическое задание |
| 32 |
|
| 14.20 -15.00 | Практическая работа | 1 | Теорема Пифагора. | МБОУ «Дроздовская ООШ» | Практическое задание |
| 33 |
|
| 14.20 -15.00 | Практическая работа | 1 | Подобие треугольников. | МБОУ «Дроздовская ООШ» | Практическое задание |
| 34 |
|
| 14.20 -15.00 | Самостоятельная работа | 1 | Итоговое занятие.
| МБОУ «Дроздовская ООШ» | Тестирование |
Методическое обеспечение программы
Представленная программа построена на принципах развивающего обучения, предполагающего формирование у детей умения самостоятельно мыслить, анализировать, обобщать, устанавливать причинно-следственные связи.
Методические занятия в объединении являются комплексными. На них используются различные виды деятельности: лекции, аналитические и эвристические беседы, наглядный (показ мультимедийных материалов, иллюстраций), постановка и формулирование проблемы, самостоятельное создание алгоритмов деятельности при решении проблем творческого и поискового характера; моделирование – преобразование объекта из чувственной формы в модель, где выделены существенные характеристики объекта (пространственно-графическая или знаково-символическая); преобразование модели с целью выявления общих законов, определяющих данную предметную область; анализ объектов с целью выделения признаков (существенных, несущественных); синтез – составление целого из частей, в том числе самостоятельное достраивание с восполнением недостающих компонентов; выбор оснований и критериев для сравнения, классификации объектов; подведение под понятие, выведение следствий; установление причинно-следственных связей, представление цепочек объектов и явлений; построение логической цепочки рассуждений, анализ истинности утверждений; доказательство; выдвижение гипотез и их обоснование; формулирование проблемы; самостоятельное создание способов решения проблем творческого и поискового характера.
Методы, в основе которых лежит способ организации занятия:
- словесный (устное изложение, беседа, рассказ, лекция и т.д.);
- наглядный (показ мультимедийных материалов, иллюстраций, готовых работ;
- наблюдение;
- показ (выполнение педагогом), работа по образцу;
- практический (выполнение работ по инструкционным картам, схемам и др.).
Методы, в основе которых лежит уровень деятельности детей:
- объяснительно-иллюстративный – дети воспринимают и усваивают готовую информацию;
- репродуктивный – учащиеся воспроизводят полученные знания и освоенные способы деятельности;
- частично-поисковый – участие детей в коллективном поиске, решение поставленной задачи совместно с педагогом;
- исследовательский – самостоятельная творческая работа учащихся.
Методы, в основе которых лежит форма организации деятельности учащихся на занятиях:
- фронтальный – одновременная работа со всеми учащимися;
- индивидуально-фронтальный – чередование индивидуальных и фронтальных форм работы;
- групповой – организация работы в группах;
- индивидуальный – индивидуальное выполнение заданий, решение проблем.
Используемые педагогические технологии
Для успешной реализации поставленных целей в организации образовательного процесса используются самые различные педагогические технологии:
- технология педагогического общения – основана на взаимодействии подростка и педагога, при котором ограждается достоинство педагога, сохраняется достоинство и корректируется поведение ребенка;
- личностно-ориентированная технология – основана на личностной ориентации образовательного процесса: педагогика сотрудничества;
- технология предъявления педагогического требования – предъявление нормы культурной жизни и организация жизнедеятельности детей;
- технология педагогической оценки поведения и поступков детей – направлена на формирование социальных норм, установок, социальной позиции и мировоззрения, является средством ориентации ребенка среди множества ценностей и анти ценностей.
- тренинг общения – создание у детей средствами групповой практической психологии различных аспектов позитивного коммуникативного опыта;
- опыта взаимопонимания, общения, поведения и т.п.
В программе используются такие формы занятий, которые мотивируют учащихся к активному слушанию, познанию изучаемого материала, а также обеспечивают наибольшую эффективность и оптимальность его восприятия, а именно: учебное занятие, практическое занятие, тренинг, интеллектуальная игра, дискуссия, защита проекта, конкурс.
Список литературы:
1. Основная литература
Вавилов В.В. и др. «Задачи по математике. Уравнения и неравенства», М, Наука, 2019
Алгебра: сб. заданий для подготовки к итоговой аттестации в 9 классе./Л. В.Кузнецова, С. Б. Суворова, Е. А. Бунимович и др.- 2-е изд.-М.: Просвещение, 2019.-191с.:ил.- (Итоговая аттестация).
Галицкий М. Л. И др. Сборник задач по алгебре для 8-9 классов:Учеб. пособие для Учащихся школ и классов с углубленным изучением математики/М. Л. Галицкий, А. М. Гольдман, Л. И. Звавич.-2-е изд. –М.: Просвещение, 2019.-271с.: ил.
ГИА: 3000 задач с ответами по математике. Все задания части / А.Л. Семенов, И.В. Ященко, Л. О. Рослова, Л. В. Кузнецова, С. Б. Суворова, И. Р. Высотский; под редакцией А.Л. Семенова, И.В. Ященко, — М.: Издательство «Экзамен», издательство МЦНМО, 2019. — 399, [1]с. (Серия «Банк заданий ГИА»)
Дорофеев Г.В. и др. «Подготовка к письменному экзамену за курс основной школы» сборник
2. Дополнительная литература
ГИА-2022. Математика: типовые экзаменационные варианты: 30 вариантов / Под ред. А.Л. Семенова, И.В. Ященко. — М.: Издательство «Национальное образование», 2020. — (ГИА-2022. ФИПИ-школе)
ГИА-2022. Экзамен в новой форме. Математика. 9 класс/ Под. Ред. И.В. Ященко- М.: Астрель, 2022.
Дорофеев Г.В. и др. «Подготовка к письменному экзамену за курс основной школы» сборник
Зейфман А.И.и др. «Сборник задач повышенной сложности по основным разделам школьного курса математики», Вологда, 2018
Королева Т.М. и др. «Пособие по математике в помощь участникам централизованного тестирования», М, 2019
Программа для общеобразовательных школ, гимназий, лицеев. Издательство Дрофа, Москва, 2019
3. Информационные ресурсы
http://schoolmathematics.ru/ege/zadanie-v10,
http://www.coolreferat.com/,
www.zadanonadom.ru,
matematikalegko.ru
http://onlinetestpad.com/ru-ru/TestView/GIA-2013-Matematika-Demonstracionnyj-variant-REALNAYA-MATEMATIKA-1659/Default.aspx
www.mathgia.ru - Открытый банк задач по математике (ОГЭ)
http://www.mathnet.spb.ru/ Дмитрий Гущин – сайт элементарной математики
http://wvvw.fipi.ru/ - ФИПИ
http://www.ege.edu.ru/ - Официальный информационный портал ЕГЭ
http://egeigia.ru/ - Информационный образовательный портал. Подготовка к экзаменам
http://uztest.ru/ онлайн тесты по по математике (ОГЭ, ЕГЭ).
http://festival.1september.ru/
http://school-collection.edu.ru/
http://www.ziimag.narod.ru/
http://www.alleng.ru/
http://bbk50.narod.ru/
http://smekalka.pp.ru/
http://pedsovet.su/load/18








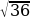 = -6 б)
= -6 б)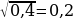 в)
в)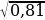 = 0,9
= 0,9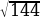
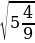
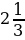 ; б)
; б) 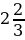 ; в)
; в)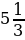
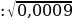
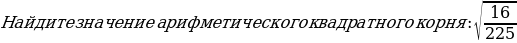
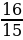 б)
б) 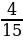 в)
в)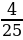
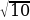 )2
)2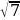 )2
)2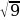 - 2
- 2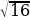
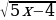 = 6
= 6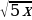 – 4 =6
– 4 =6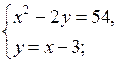
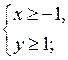
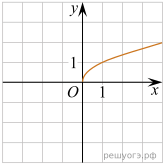
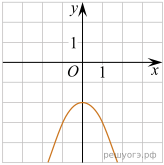
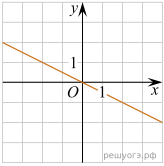

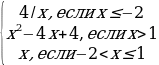
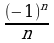 . Какое из чисел не
. Какое из чисел не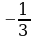 В.
В. 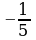 Г.
Г. 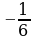
 . Определите, сколько необходимо закупить пленки
. Определите, сколько необходимо закупить пленки  . Дизайнер Павел получил заказ на декорирование чемодана цветной бумагой. По рисунку определите, сколько бумаги (в см2) необходимо закупить Павлу, чтобы оклеить всю внешнюю поверхность чемодана, если каждую грань он будет обклеивать отдельно (без загибов).
. Дизайнер Павел получил заказ на декорирование чемодана цветной бумагой. По рисунку определите, сколько бумаги (в см2) необходимо закупить Павлу, чтобы оклеить всю внешнюю поверхность чемодана, если каждую грань он будет обклеивать отдельно (без загибов).
 . Мальчик прошел от дома по направлению на восток 800 м. Затем повернул на север и прошел 600 м. На каком расстоянии (в метрах) от дома оказался мальчик?
. Мальчик прошел от дома по направлению на восток 800 м. Затем повернул на север и прошел 600 м. На каком расстоянии (в метрах) от дома оказался мальчик? . Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 15 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 8 м. Найдите длину троса.
. Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 15 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 8 м. Найдите длину троса. . Длина стремянки в сложенном виде равна 1,85 м, а ее высота в разложенном виде составляет 1,48 м. Найдите расстояние (в метрах) между основаниями стремянки в разложенном виде.
. Длина стремянки в сложенном виде равна 1,85 м, а ее высота в разложенном виде составляет 1,48 м. Найдите расстояние (в метрах) между основаниями стремянки в разложенном виде.
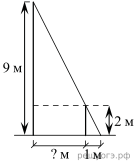 . На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?
. На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?
 . Проектор полностью освещает экран A высотой 80 см, расположенный на расстоянии 120 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 330 см, чтобы он был полностью освещен, если настройки проектора остаются неизменными?
. Проектор полностью освещает экран A высотой 80 см, расположенный на расстоянии 120 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 330 см, чтобы он был полностью освещен, если настройки проектора остаются неизменными?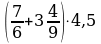
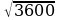 ,
,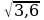 ,
, 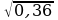 - является иррациональным?
- является иррациональным?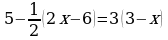

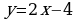 2)
2) 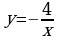 3)
3) 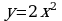 4)
4) 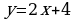
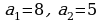 . Найдите сумму первых 20 членов этой прогрессии.
. Найдите сумму первых 20 членов этой прогрессии.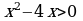 1)
1) 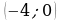
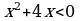 2)
2) 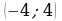
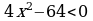 3)
3) 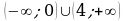
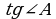 .
.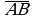 с началом в точке
с началом в точке 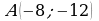 имеет координаты
имеет координаты 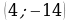 . Найдите ординату точки B.
. Найдите ординату точки B.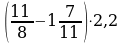
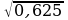 ,
,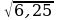 ,
, 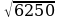 - является рациональным?
- является рациональным?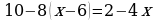
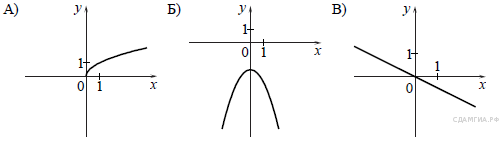
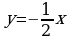 2)
2) 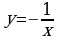 3)
3) 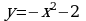 4)
4) 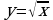
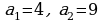 . Найдите сумму первых 10 членов этой прогрессии.
. Найдите сумму первых 10 членов этой прогрессии.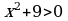 1)
1) 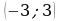
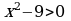 2)
2) 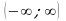
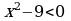 3)
3) 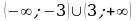
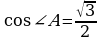 . Найдите высоту, проведенную к основанию.
. Найдите высоту, проведенную к основанию.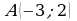 имеет координаты
имеет координаты 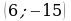 . Найдите абсциссу точки B.
. Найдите абсциссу точки B.









