Производная функция

Урок по теме "Производная (11-й класс)

Цель: cбобщить и расширить знания по теме «Производная».

Задачи урока:

• Учебно-познавательная: формировать умение применять понятие производной в стандартных и нестандартных ситуациях;

• Развивающая: развивать умения и навыки самостоятельно применять знания для решения практических и теоретических задач;

Ход урока

1. Слово учителя.

Тема нашего урока «Производная и её применение». На уроке мы должны обобщить и систематизировать материал. Девизом нашего урока станут слова французского математика «Дорогу осилит идущий, а математику – мыслящий».

Перед нами стоит задача – показать знание формул по теме и умение применять производную при решении практических задач, подготовиться к контрольной работе и ЕГЭ.

2. Проверка домашнего задания.

В начале урока рассмотрим сложные задания из домашней работы.

3. История возникновения производной.

Ну а сейчас мы послушаем историю возникновения понятия производная. (

4. Диктант.

У математиков существует свой язык – это формулы. Проверим как вы знаете формулы. Подготовьтесь к диктанту.

1. Напишите правила дифференцирования: а) (f ∙ g)`; б) (f / g)`.

2. Запишите производную функций: a) (x)^p; б) e^kx; в) a^x; г) sin(kx + b).

3. Напишите формулу уравнения касательной к графику функции f(x) в точке с абсциссой x₀.

4. Запишите формулу, выражающую геометрический смысл производной.

5. Сформулируйте определение промежутков монотонности функции.

6. Напишите определение стационарной точки.

5. Какие задачи решаются с помощью производной.

Перед тем как решать задачи давайте вспомним, где применяется производная?

6. Решение задач.

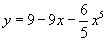
Б Тело движется прямолинейно по закону S(t) = t³ – t. (Координаты измеряются в метрах, время – в секундах)
Определите: 1) скорость в момент времени t = 3 c.; 2) ускорение движения в момент времени t = 0,2 c.

В Найдите промежутки монотонности функции y = f(x), если изображен график её производной.

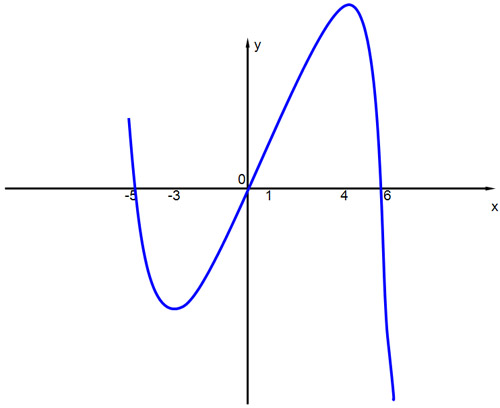
Г Какие из точек х1, х2, х3, … х10 являются точками экстремума, точками перегиба?

Д Железнодорожное полотно представляет собой графическое изображение функции y = x³. Найти интервалы выпуклости вверх, выпуклости вниз.

Е В сопротивлении материалов доказывают, что сопротивление изгибу балки прямоугольного сечения пропорционально её ширине х и квадрату её высоты у. P=kxy². Какое сечение должна иметь балка железнодорожного моста наибольшего сопротивления изгибу, вырезанная из цилиндрического бревна радиуса R?

7. Самостоятельная работа.

1. Найдите точки минимума функции f(x)= х² – 3х.
   1) 0;   2) 2;   3) -2;   4) 1/5.

2. Найдите производную функции y = (-2х + 3)⁸
   1) -16(-2х + 3)⁷;   2) 24(-2х + 3)⁷;   3) 8(-2х + 3)⁷;   4) -8(-2х + 3)⁷.

3. Найдите угловой коэффициент касательной, проведённой к графику функции f(x) = 9x – 4x³ в его точке с абсциссой х = 1.
   1) -3;   2) 0;   3) 3;   4) 5.

4. Найдите наибольшее и наименьшее значение функции f(x)= -x³ + 2x² – 8x + 1 на отрезке [-2; 1].

8. Творческое домашнее задание.

10. Итог урока.