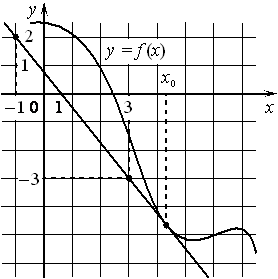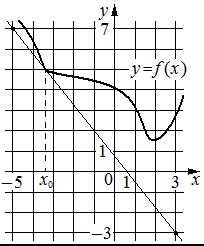Конспект урока на тему: Производная и её геометрический смысл
Цели урока:
Обучающие:
повторить основные формулы и правила дифференцирования, физический и геометрический смысл производной;
вывести уравнение касательной к графику дифференцируемой функции;
сформировать умение комплексного применения знаний, умений, навыков и их перенос в новые условия;
проверить знания, умения, навыки учащихся по данной теме.
Развивающие:
способствовать развитию мыслительных операций: анализ, синтез, обобщение;
оказать помочь в формировании умений самооценки и взаимооценки;
развивать познавательную активность, вычислительные навыки.
Воспитательные:
воспитывать добросовестное отношение к труду, инициативность, организованность.
Тип урока:
комбинированный
Оборудование: программа презентаций Microsoft Office PowerPoint, презентация, компьютер, мультимедиа проектор.
УМК: Ш.А. Алимов, Ю.М.Колягин и др. «Алгебра и начала анализа» учебник для 10-11 классов общеобразовательных учреждений. М.: Просвещение, 2022года.
План урока:
Организационный момент (1 мин)
Проверка домашнего задания (3 мин)
Проверка знаний (17 мин)
Подготовка обучающихся к активному усвоению знаний (1 мин)
Усвоения новых знаний (5 мин)
Закрепления новых знаний (10 мин)
Подведение итогов урока (1 мин)
Домашнее задание (2 мин)
Организационная структура урока
I. Организационный момент
Приветствие класса. Проверка готовности класса к уроку.
Учитель знакомит с темой, целями и ходом урока.
II. Проверка домашнего задания
№ 858, 859
III. Проверка знаний
Устный опрос:
Сформулируйте определение производной.
Определение: Пусть функция f (x) определена на некотором промежутке, х – точка этого промежутка и число h # 0 такое, что х + h также принадлежит данному промежутку. Тогда предел разностного отношения 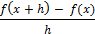
при h → 0 (если этот предел существует) называется производной функции
f (х) в точке х и обозначается f '(х). Таким образом,
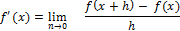
Как называется операция нахождения производной?
Операция нахождения производной называется дифференцированием.
Какая функция называется дифференцируемой в точке?
Если функция f (х) имеет производную в точке х, то эта функция называется дифференцируемой в этой точке.
Какая функция называется дифференцируемой на некотором промежутке?
Если функция f (х) имеет производную в каждой точке некоторого промежутка, то говорят, что эта функция дифференцируема на этом промежутке.
В чем заключается физический (механический) смысл производной?
Тангенс угла наклона касательной есть величина, показывающая мгновенную скорость изменения функции в данной точке.
В чем заключается геометрический смысл производной?
Значение производной функции в точке равно угловому коэффициенту касательной к графику функции в этой точке.
Сформулируйте правило нахождения производной суммы, произведения, частного.
«Верно-неверно»
Если ученик согласен с ответом – он ставит у себя в тетради «+», если – нет «-«.
Цель данного задания – понимание смысла теоретических знаний.
1.Если функция дифференцируема в точке, то она в этой точке непрерывна?
Да
2.Если функция непрерывна в точке, то она в этой точке дифференцируема?
Нет
3. Верно ли, что тангенс угла наклона касательной к графику функции – есть значение производной функции в точке касания?
Да
4.Верно ли, что производная суммы функций равна сумме производных функций?
Да
5.Верно ли, что производная функции у = ln x имеет производную в точке
х = - 5?
Нет
6.Верно ли, что первая производная пути от времени – это есть мгновенная скорость материальной точки?
Да
7.Верно ли, что функция у =cos x дифференцируема на множестве действительных чисел?
Да
Ответы: + - + + - + +
Решение задач
Решение задач на нахождение производной в точке, углового коэффициента касательной к графику функции.
Данные задачи учащиеся решают с использование интерактивной доски, каждая задача изображается на отдельном слайде. (1 – 11 слайд)
Учащиеся по мере движения слайдов обсуждают решения задач.
Самостоятельная работа: 5 заданий из открытого банка заданий (1в., 2 в.)
ИЗ ОТКРЫТОГО БАНКА ЗАДАНИЙ 1в
На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D.
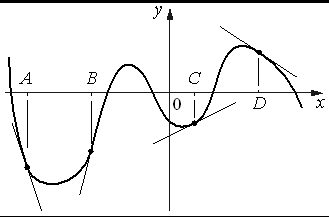
В правом столбце указаны значения производной функции в точках A, B, C и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.
ТОЧКИ ЗНАЧЕНИЯ ПРОИЗВОДНОЙ
A 1) 0,5
B 2) − 0,7
C 3) 4
D 4) −3
В таблице под каждой буквой укажите соответствующий номер.
На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D.
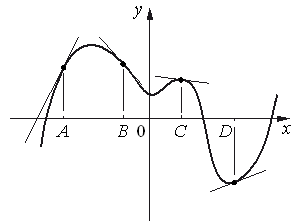
В правом столбце указаны значения производной функции в точках A, B, C
и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.
ТОЧКИ ЗНАЧЕНИЯ ПРОИЗВОДНОЙ
A 1) − �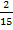 �
�
B 2) 2
C 3) �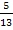 �
�
D 4) − 1 �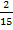 �
�
В таблице под каждой буквой укажите соответствующий номер.
На рисунке изображены график функции y=f(x) и касательная к этому графику, проведённая в точке с абсциссой x0. Найдите значение производной функции f(x)
в точке x0.
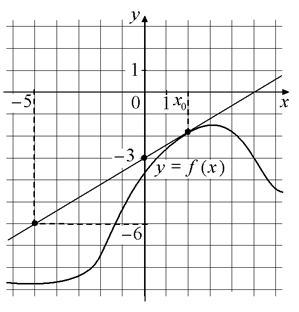
На рисунке изображены график функции y=f(x) и касательная к этому графику, проведённая в точке с абсциссой x0. Найдите значение производной функции f(x)
в точке x0.
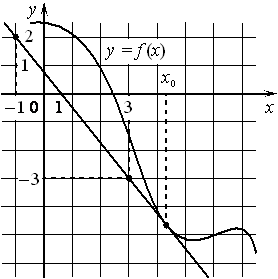
На рисунке изображены график функции y=f(x) и касательная к этому графику, проведённая в точке с абсциссой x0. Найдите значение производной функции f(x)
в точке x0.
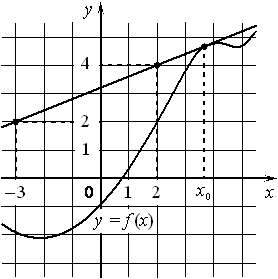
ИЗ ОТКРЫТОГО БАНКА ЗАДАНИЙ 2в
1.На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D.
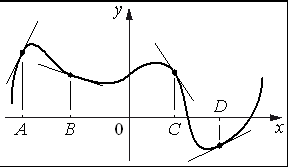
В правом столбце указаны значения производной функции в точках A, B, C и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.
ТОЧКИ ЗНАЧЕНИЯ ПРОИЗВОДНОЙ
A 1) − 1,5
B 2) 0,5
C 3) 2
D 4) − 0,3
таблице под каждой буквой укажите соответствующий номер.
2. На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D.
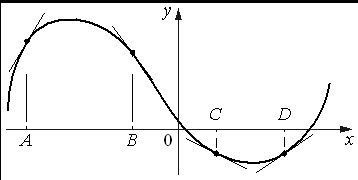
В правом столбце указаны значения производной функции в точках A, B, C и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.
ТОЧКИ ЗНАЧЕНИЯ ПРОИЗВОДНОЙ
A 1) ⅔
B 2) - ½
C 3) -1⅓
D 4) 1⅔
В таблице под каждой буквой укажите соответствующий номер.
3.На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой
x0. Найдите значение производной функции f(x) в точке x0.
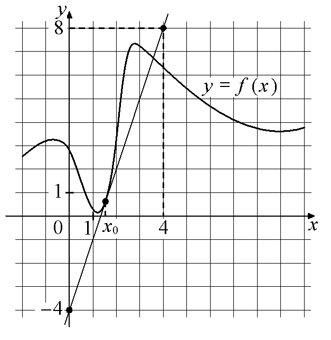
4. На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой
x0. Найдите значение производной функции f(x) в точке x0.
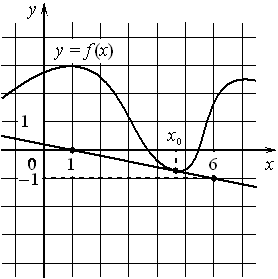
5. На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой
x0. Найдите значение производной функции f(x) в точке x0.
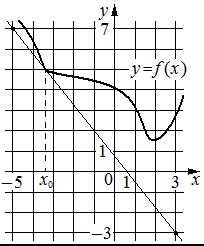
V. Подготовка обучающихся к активному усвоению знаний. Усвоение новых знаний.
Вывод уравнения касательной к графику дифференцированной функции y = f (x) в точке ( х0; f (x0) ).
Закрепления новых знаний.
Запишите алгоритм нахождения уравнения касательной к графику функции y = f (x) в точке х0.
Решаем №860 (1,3)
VII. Подведение итогов урока.
| Ф.И. обучающегося | Теоретический опрос | Верно-неверно | Самостоятельная работа | Работа у доски | Итого |
| 1. |
|
|
|
|
|
| 2. |
|
|
|
|
|
VIII. Домашнее задание.
№860(2,4,6), 866(2,4)
8