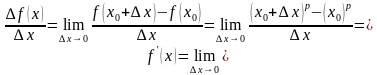Данная разработка предназначена для учеников 11 класса, обучающихся по учебнику А.Ш. Алимова. В теоретической части содержится вывод формул для нахождения производной простых степенных функций, общей формулы степенной функции, а также вывод формулы для нахождения производной сложной степенной функции. Практическая часть содержит задания для отработки полученных знаний и умений.
Просмотр содержимого документа
«Производная степенной функции.»
Производная степенной функции.
Используя определение производной, найдём сначала производную самой простой степенной функции  .
.
По определению производной,
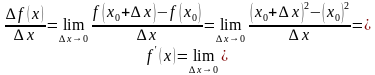


Значит, 
Теперь найдём производную кубической функции 

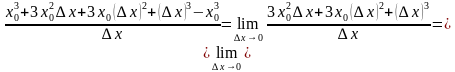

Значит, 
Найдём теперь производную степенной функции с отрицательным показателем  .
.
Преобразуем эту функцию:  и найдём её производную.
и найдём её производную.


Значит,  или
или  .
.
И ещё одна степенная функция с отрицательным показателем:  .
.
Преобразуем эту функцию:  и найдём её производную.
и найдём её производную.



Значит,  или
или 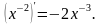
Обобщим все рассмотренные примеры и выведем общую формулу производной степенной функции  .
.
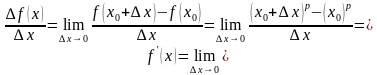
Воспользуемся формулой: . Тогда,
Значит, 
По этой формуле находим, что
Мы вывели формулу простой степенной функции, однако, такие функции встречаются не всегда, очень часто мы имеем дело со сложными функциями вида  . Формула производной этой функции выводится аналогичным образом. Кто всерьёз интересуется математикой, рекомендую эту формулу вывести самостоятельно.
. Формула производной этой функции выводится аналогичным образом. Кто всерьёз интересуется математикой, рекомендую эту формулу вывести самостоятельно.
Чтобы найти производную сложной степенной функции, нужно взять производную степени и умножить на производную основания степени.
Найти производную функции:
Найти  , если:
, если:
При каких значениях  производная функции
производная функции  равна
равна  ?
?
При каких значениях  производная функции
производная функции  равна
равна  ?
?
Решить уравнение  , если
, если  .
.
Решить уравнение  , если
, если  .
.
Найти такие значения  , при которых производная функции
, при которых производная функции  принимает указанное значение.
принимает указанное значение.
Упростив выражение для  , найдите
, найдите  , если:
, если:
Упростив выражение для  , найдите
, найдите  , если:
, если:
2







 .
.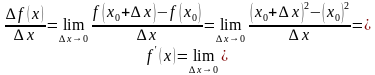





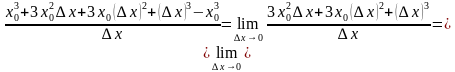


 .
. и найдём её производную.
и найдём её производную.

 или
или  .
. .
. и найдём её производную.
и найдём её производную.


 или
или 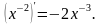
 .
.