Простейшие задачи в координатах

z

I I I I I

I I I I I I I I

I I I

I I I I I

I I I I I

Найти координаты точек А, В, С и

векторов ОА, ОВ, ОС

В

OA{ -1 ; 3 ; -6 }

A (-1 ; 3 ; -6 )

С

B( - 2;-3; 4)

OB{ - 2;-3; 4}

k

O

y

I I I I I I I I

C( 3;-2; 6)

j

i

OC{ 3;-2; 6}

x

А

2

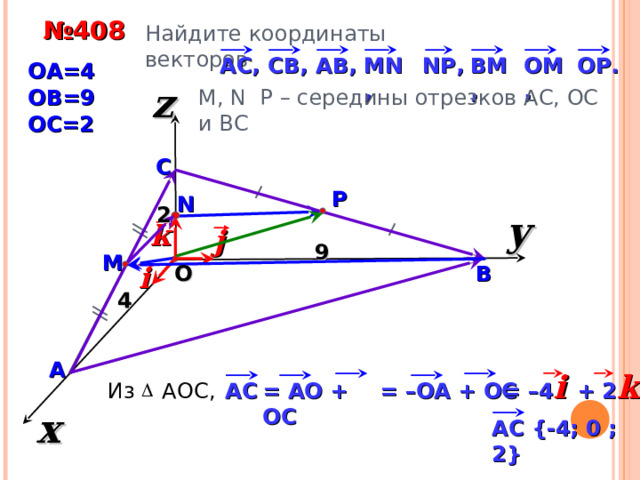
№ 4 08

Найдите координаты векторов

MN,

AB,

CB,

BM,

OM,

OP.

NP,

AC,

OA=4

z

M, N P – середины отрезков АС, ОС и ВС

OB=9

OC=2

С

Р

N

2

y

k

j

9

М

O

i

В

4

А

= –4 i + 2 k

Из АОС ,

= –О A + ОС

= A О + ОС

AC

x

AC {-4; 0 ; 2}

3

Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.

Коллинеарные, сонаправленные векторы

a

c

b

b

c

b

c

a

a

Нулевой вектор условимся считать сонаправленным с любым вектором.

o

o

o

a

c

b

4

Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.

Коллинеарные,

противоположно направленные векторы

c

b

a

b

c

b

a

5

Коллинеарны ли векторы

8

6

3

a { 3 ; 6 ; 8 };

6

1 6

12

b { 6 ; 12 ;1 6 }

1

1

=

=

=

a

=

b

a

= 2

b

или

2

2

b

a

Векторы и коллинеарны.

*

Замените так, чтобы векторы были коллинеарны.

a { 2 ; ; 6 };

-1,5

12

b { 4 ; -3 ; }

*

*

c {0; 2; };

0

-12

f { ; - 0,5; 3 }

*

*

6

Векторы называются компланарными , если при откладывании их от одной и той же точки они будут лежать в одной плоскости.

Другими словами, векторы называются компланарными , если имеются равные им векторы, лежащие в одной плоскости.

c

c

b

b

a

7

Любые два вектора компланарны.

Три вектора, среди которых имеются два коллинеарных, также компланарны.

Признак компланарности

c

Если вектор можно разложить по векторам

и , т.е. представить в виде

где x и y – некоторые числа, то векторы , и

компланарны.

c = xa + yb

a

b

«Геометрия 10-11» Л.С. Атанасян и др.

a

b

c

8

Компланарны ли векторы

и

6

-3

a { 2 ; 6 ; -3 };

2

i

6

18

-9

b { 6 ; 18 ; -9 }

1

=

=

=

3

a

b

Векторы и коллинеарны.

a

b

i

Векторы , , компланарны.

Компланарны ли векторы

и

a { 2 ; 4; 3 };

0

MM

b { 6 ; 1 1; -9 };

=

Нулевой вектор коллинеарен любому вектору.

Значит, эти векторы компланарны.

9

Компланарны ли векторы

и

n { 2 ; 6 ; -3 };

{0; 1; 0}

j

f {0; 5; 0}

j

f

Векторы и коллинеарны.

n

f

j

Векторы , , компланарны.

Компланарны ли векторы

и

a {-3;-3; 0};

i {1; 0; 0};

j {0; 1; 0}

10

1 уравнение

2 уравнение

3 уравнение

a = x i + y j

Компланарны ли векторы

a {-3;-3; 0};

– 3 = x 1 + y 0

i { 1; 0; 0};

– 3 = x 0 + y 1

j { 0; 1; 0}

0 = x 0 + y 0

Признак компланарности

a

Проверим, можно ли разложить, например , вектор по

векторам и .

i

j

y

x

a = x i + y j

Существуют ли такие числа и , что

415а

11

Каждая координата вектора равна разности

соответствующих координат его конца и начала.

Выразим координаты вектора АВ через координаты

его начала А и конца В.

= –О A + О B

AB

= A О + О B

Из АО B,

z

OA { x 1 ; y 1 ; z 1 }

B ( x 2 ; y 2 ; z 2 )

OB { x 2 ; y 2 ; z 2 }

y

О

– OA {- x 1 ; -y 1 ; -z 1 }

+

OB { x 2 ; y 2 ; z 2 }

*

{ x 2 - x 1 ; y 2 -y 1 ; z 2 -z 1 }

AB

OB – OA

x

A ( x 1 ; y 1 ; z 1 )

12

A ( 3;5;7)

–

B

A

( 3;5;7),

( 5;4;-1),

AB

B ( 5;4;-1)

AB{2;-1;-8}

O

N

( 3;2;-3),

ON{3; 2;-3}

ON

( 0;0;0),

Радиус-вектор

P ( 2;-1;0)

–

( 2;-1;0),

P

( 4;-4;2),

C

PC

C ( 4;-4;2)

PC{2;-3; 2}

( -4;0;-4),

R

TR

( 0;5;-1),

T

R ( -4;0;-4)

–

T ( 0; 5;-1)

D

OD

( -3;-4;0),

O

( 0;0;0),

TR{-4;-5;-3}

OD{-3;-4; 0}

Радиус-вектор

13

Найдите координаты

векторов

M ( -2;7;3)

D ( -5;7;-2)

–

–

P ( -5; 1;4)

R ( 2; 7;1)

R (2 ; 7 ;1) ; M(-2;7;3); RM

RM{-4;0;2}

PD{ 0; 6;-6}

P ( -5;1;4) ; D(-5;7;-2); PD

A ( 0; 3;4)

N ( 0; 5;-3)

–

–

R ( -3;0;-2) ; N(0;5;-3); RN

R ( -3;0;-2)

B ( -4;0;-3)

RN{3; 5;-1}

BA{4; 3;7}

A ( 0;3;4) ; B(-4;0;-3); BA

.

B ( -2;0;-3)

T ( -2;-7;0)

A ( - 2 ; 7 ;5) ; B(-2;0;-3); AB

–

–

A ( -2;7;5)

R ( -7; 7;-6)

R ( -7; 7 ;-6) ; T(-2;-7;0); RT

AB{0;-7;-8}

RT{5;-14;6}

14

Найти координаты векторов.

{ }

R (2 ; 7 ;1) ; M(-2;7;3); RM

{ }

P ( -5;1;4) ; D(-5;7;-2); PD

{ }

R ( -3;0;-2) ; N(0;5;-3); RN

{ }

A ( 0;3;4) ; B(-4;0;-3); BA

{ }

A ( - 2 ; 7 ;5) ; B(-2;0;-3); AB

{ }

R ( -7; 7 ;-6) ; T(-2;-7;0); RT

Вводите ответы в текстовые поля, не делая пробелов

Найти координаты векторов.

3 a { }

a { 2 ; 4;-1};

- 2 b { }

b { -2 ; 0 ;1,5};

- 3 d { }

2

d { -2 ;-3; };

3

- c { }

c { 2;-5 ;0};

0,5 e { }

e {2;-3;8};

- 2 f { }

1

f( 0; 5;- };

2

Вводите ответы в текстовые поля, не делая пробелов

- a { }

Найти координаты векторов,

противоположных данным.

a { 2 ; 4;-5};

- b { }

b { -2 ; 0 ;-1};

- d { }

d {0; 0; 0};

– j { }

– i { }

– k { }

Вводите ответы в текстовые поля, не делая пробелов

Найти координаты векторов.

a +c { }

c {3; 2;-3};

a { 2 ; 4; 3};

b+d { }

b { -2 ; 0 ; 4};

d { -2 ;-3;-1};

c +e { }

e {2;-3;-9};

c { 2;-5 ; 4};

d { -2 ;-3;7};

f( 0; 5;-3};

f - d { }

b - d { }

d { -2 ;-3;-4};

b { -2 ; 0 ;-1};

a { 2 ; 4;0};

a - c { }

c {3; 2;-9};

Вводите ответы в текстовые поля, не делая пробелов

Планиметрия

B

C

A

«Геометрия 7-9» Л.С. Атанасян и др.

O

19

Координаты середины отрезка

OA{ x 1 ; y 1 ; z 1 }

+

1

OC

OB{ x 2 ; y 2 ; z 2 }

(OA+OB)

=

OC

2

:2

OA+OB{ x 1 + x 2 ; y 1 + y 2 ; z 1 +z 2 }

z

A ( x 1 ; y 1 ; z 1 )

C ( x ; y ; z )

B ( x 2 ; y 2 ; z 2 )

y

О

y 1 + y 2

x 1 + x 2

z 1 + z 2

1

{ ; ; }

(OA+OB)

x

2

2

2

2

*

y 1 + y 2

z 1 + z 2

x 1 + x 2

y = ;

z =

x = ;

2

2

2

20

Каждая координата середины отрезка равна полусумме соответствующих координат его концов.

z 1 + z 2

x 1 + x 2

y 1 + y 2

{ ; ; }

OC

z

2

2

2

A ( x 1 ; y 1 ; z 1 )

y 1 + y 2

z 1 + z 2

x 1 + x 2

C ( ; ; )

2

2

2

B ( x 2 ; y 2 ; z 2 )

y

О

Полусумма аппликат

x

*

Полусумма ординат

z 1 + z 2

*

z =

Полусумма абсцисс

y 1 + y 2

*

2

y = ;

x 1 + x 2

2

x = ;

2

21

№ 424 ( a ) Найдите координаты середины отрезка

A ( 0; 3;-4),

B ( -2;2;0), середина – точка

( ; ; )

M

-1

2,5

-2

Полусумма абсцисс

x 1 + x 2

0+(-2)

x = ;

x =

= -1

2

2

Полусумма ординат

y 1 + y 2

3 +2

y = ;

y =

= 2,5

2

2

Полусумма аппликат

z 1 + z 2

-4 +0

z = ;

z =

= -2

2

2

22

Найдите координаты

середины отрезков

4 + 2

2+(-2)

7 + 7

C ( 0; 7; 3 )

( ; ; )

R (2 ; 7 ;4) ; M(-2;7;2); C

2

2

2

1 + 7

3 +(-9)

-5+(-5)

C ( -5; 4;-3 )

( ; ; )

P ( -5;1;3) ; D(-5;7;-9); C

2

2

2

0+5

-3+(-5)

-3+0

C ( -1,5;2,5;-4 )

( ; ; ) ;

R ( -3;0;-3) ; N(0;5;-5); C

2

2

2

0+(-4)

-6+2

9+(-6)

( ; ; ) ;

C ( -2;-2;1,5 )

A ( 0;-6;9) ; B(-4;2;-6); C

2

2

2

0+(-4)

7 + 0

7+(-2)

( ; ; ) ;

C ( 2,5; 3,5;-2 )

A ( 7; 7 ;0) ; B(-2;0;-4); C

2

2

2

0+0

-7+(-2)

4+(-7)

( ; ; ) ;

C ( -4,5;-1,5;0 )

R ( -7;4;0) ; T(-2;-7;0); C

2

2

2

23

z 1

y 1

x 1

Обратная задача.

A ( 5; 4;-6)

y

z

x

A ( 5; 4; -6);

C(-3; 2; 10) – середина отрезка AB

C(-3; 2;10)

Дано:

Найти:

z 2

x 2

y 2

B ( a ; b;c )

B ( a ; b;c )

z 1 + z 2

y 1 + y 2

x 1 + x 2

z =

y = ;

x = ;

2

2

2

-6 + c

4 + b

2

5 + a

2

10 =

2

2 = ;

-3 = ;

2

2

2

4 = 4 + b

– 6 = 5 + a

20 = -6 + c

a = – 11

b = 0

c = 26

B ( -11; 0;26)

24

Вычисление длины вектора по его координатам

z

a { x ; y ; z }

По правилу параллелепипеда

OA 2 = OA 1 2 + OA 2 2 + OA 3 2

OA 2 = OA 1 2 + OA 2 2 + OA 3 2

A 3

=

x

OA 1 = x i

A

z k

a

OA 2 = y j

y

=

y j

y

О

OA 3 = z k

z

=

A 2

x i

A 1

2

2

2

2

a

+ +

=

z

x

y

x

*

2

2

2

a

y

z

x

=

+ +

25

z

d

Расстояние между двумя точками

M 2 ( x 2 ; y 2 ; z 2 )

M 2 ( x 2 ; y 2 ; z 2 )

–

M 1 ( x 1 ; y 1 ; z 1 )

y

О

M 1 M 2 { x 2 –x 1 ; y 2 –y 1 ; z 2 –z 1 }

*

x

M 1 ( x 1 ; y 1 ; z 1 )

2

2

2

a

+ +

y

z

x

=

M 1 M 2 =

( x 2 –x 1 ) 2 +( y 2 –y 1 ) 2 +( z 2 –z 1 ) 2

*

d =

( x 2 –x 1 ) 2 +( y 2 –y 1 ) 2 +( z 2 –z 1 ) 2

26

№ 426 ( a ) Найдите длину вектора АВ

A (-1 ; 0 ;2) и B(1;-2;3)

a

1 способ

=

x 2 + y 2 + z 2

B(1;-2;3)

1 )

AB =

–

= 9

= 3

2 2 + (-2) 2 +1 2

2)

A (-1 ; 0 ;2)

AB{2;-2;1}

2 способ

( x 2 –x 1 ) 2 +( y 2 –y 1 ) 2 +( z 2 –z 1 ) 2

AB =

(1 + 1) 2 +( – 2 – 0) 2 +(3–2) 2

AB =

27

№ 426 (б) Найдите длину вектора АВ

A (-35 ; -17 ;2 0 ) и B( -34 ;- 5 ; 8 )

a

=

x 2 + y 2 + z 2

1 способ

2)

1 )

B( -34 ; - 5 ; 8 )

1 способ

AB =

–

1 2 + 12 2 + (- 1 2) 2 =

A (-35 ; -17 ;2 0 )

= 17

= 289

AB{ 1 ; 1 2; - 1 2 }

( x 2 –x 1 ) 2 +( y 2 –y 1 ) 2 +( z 2 –z 1 ) 2

AB =

2 способ

2 способ

AB =

( -34 + 35 ) 2 +( – 5 + 17 ) 2 +( 8 –2 0 ) 2

Найти координаты середин отрезков.

( )

R (2 ; 7 ; 4 ) ; M(-2;7;2); C

( )

P ( -5;1;3) ; D(-5;7;-9); C

( )

R ( -3;0;-3) ; N(0;5;-5); C

( )

A ( 0;-6;9) ; B(-4;2;-6); C

( )

A ( 7; 7 ;0) ; B(-2;0;-4); C

( )

R ( -7;4;0) ; T(-2;-7;0); C

Вводите ответы в текстовые поля, не делая пробелов .