| Казан шәһәре Совет районының «181 нче күп профильле мәктәбе» гомуми белем муниципаль бюджет учреждениесе 420081, Казан шәһәре, Тулпар урамы, 2 нче йорт | 
| Муниципальное бюджетное общеобразовательное учреждение «Многопрофильная школа №181» Советского района г. Казани 420081, г. Казань, ул. Тулпар, д. 2 |
«Согласовано» Утверждаю:
Зам директора МБОУ Директор МБОУ
«Многопрофильная школа №181» «Многопрофильная школа №181»
__________ /Перемитина А.Х.. / __________/Абдуллина Д.А. /
29.08.2022 Приказ №_260 от 29.08.2022.
Рабочая программа
дополнительного образования
«Проценты в нашей жизни»
(срок реализации – 1 год; возраст 14-17 лет)
Разработала: Айзатуллова Ф.М,
учитель математики –высшей
квалификационной категории
2020-2021 учебный год
Пояснительная записка
Кружок «Проценты в нашей жизни» ориентирован на подготовку учащихся по естественно-научному профилю и позволяет осуществлять задачи выбора направления дальнейшего обучения.
Основной целью курса является систематизация, обобщение и углубление знаний, полученных школьниками при изучении темы «Проценты» в школьном курсе. Этим обусловлен отбор содержания данной программы. Содержание программы иллюстрирует применение математики в повседневной жизни, знакомит учащихся с некоторыми историческими сведениями. Решая задачи данного курса, учащиеся учатся применять свои знания к решению повседневных бытовых проблем, вопросов рыночной экономики и задач технологии производства. При решении задач очевидны межпредметные связи с химией, физикой, экономикой, что позволяет повысить учебную мотивацию учащихся.
Задачи финансовой математики представляют в настоящее время интерес не только для будущих финансистов и экономистов, но и для всех людей. В жизни каждый из нас ежедневно встречается с ценами на товары и услуги. С такими задачами приходится иметь дело при оформлении в банке сберегательного вклада или кредита, покупке товара в рассрочку, при выплате пени, налогов, страхования. И именно школьная математика в ответе за то, чтобы эти встречи не оборачивались для людей финансовыми потерями. Вопросы, рассматриваемые в курсе, тесно примыкают к основному курсу, но не дублируют его. Кроме того, данный курс способствует совершенствованию и развитию важнейших математических знаний и умений, предусмотренных школьной программой, помогает оценить свои возможности по математике и осознанно выбрать направление дальнейшего обучения.
Цель курса:
расширить представления учащихся о процентных вычислениях, показав широту применения процентных расчетов в реальной жизни; способствовать осознанному выбору направления дальнейшего обучения; повысить уровень компетентности.
Задачи курса:
сформировать умения производить процентные вычисления, необходимые для применения в практической деятельности;
научить решать основные задачи на проценты;
привить учащимся основы экономической грамотности.
В программе приводится примерное распределение учебного времени, включающее план занятий. Для реализации целей и задач программы предполагается использовать следующие формы учебных занятий: лекции, семинары, практикумы.
Разнообразный дидактический материал дает возможность отбирать дополнительные задания для учащихся разной степени подготовки.
Тип кружка: предметный (поддерживающий, расширяющий и углубляющий знания по математике).
Объем программы: 136 часов.
Результативность курса
Реализация программы предусматривает динамику становления и развития интересов обучающихся от увлеченности до компетентного социального и профессионального самоопределения.
Планируемые результаты
Метапредметные результаты
Формируемые регулятивные УУД:
Совместно с учителем обнаруживать и формулировать проблему.
Планировать деятельность (в соответствии с поставленной задачей и условиями ее реализации) и последовательность выполнения отдельных действий в её составе.
Высказывать свои версии и предлагать способы их проверки (на основе продуктивных заданий).
Работая по предложенному плану, использовать необходимые средства (справочные пособия, инструменты, подручные средства).
Определять успешность выполнения своего задания, причины трудностей, степень достижения запланированных результатов.
Формируемые познавательные УУД:
навыки решения проблем творческого и поискового характера;
навыки поиска (в информационных источниках и в открытом информационном пространстве), анализа, интерпретации и представления информации;
навыки выбора наиболее эффективных способов действий, в том числе в ситуации исследования.
Формируемые коммуникативные УУД:
умение выполнять различные роли в группе (лидера, исполнителя, критика);
умение координировать свои усилия с усилиями других;
умение формулировать собственное мнение и позицию, с достаточной полнотой и точностью выражать свои мысли;
понимание возможности существования у людей различных точек зрения, умение ориентироваться на позицию партнера в общении и взаимодействии, стремление к координации различных позиций в сотрудничестве, умение договариваться и приходить к общему решению в совместной деятельности.
Предметные результаты
В результате прохождения программы школьники получат более полное представление о математике как о сфере человеческой деятельности, о её роли в познании и практике, а также научатся:
Видеть математическую задачу в контексте проблемной ситуации, в окружающей жизни; распознавать математические понятия и применять их при решении задач практического характера.
Моделировать практические ситуации средствами математики, способ деятельности через использование схем, интерпретировать результат решения задачи.
Решать простейшие комбинаторные задачи путём осмысления их практического значения и с применением известных правил.
Применять навыки инструментальных вычислений, некоторые приёмы быстрого решения практических задач.
Выдвигать гипотезы при решении практических задач и понимать необходимость их проверки.
Применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач.
Велика также роль процентов и в повседневной жизни, очень часто приходится решать задачи типа «Товар стоит а рублей, потом его цену снизили на р %, затем еще на b %. Сколько стал стоить товар?» Решение даже этой простейшей задачи на проценты у многих вызывает затруднение. Поэтому, изучение наиболее часто встречающихся типов задач на проценты, актуально.
Таким образом, программа кружка включает в себя обязательный минимум, показывает значимость процентов в повседневной жизни, в торговле, в сельском хозяйстве, в банковском деле, при изучении таких школьных предметов как физика, химия, география, экология, биология, экономика, ликвидирует разрыв между школьной программой и заданиями государственной итоговой аттестации.
Учебно-тематический план
| № п/п | Тема | Всего часов | Теория | Практика |
| 1 | Введение. Что такое процент? Историческая справка | 1 | 1 |
|
| 2 | Проценты от числа | 2 | 1 | 1 |
| 3 | Проценты в бизнесе | 2 | 1 | 1 |
| 4 | Проценты в экономике | 2 | 1 | 1 |
| 5 | Проценты в статистике | 1 |
| 1 |
| 6 | Игра «Брейн-ринг» | 2 |
| 2 |
| 7 | Процентные повышения | 2 | 1 | 1 |
| 8 | Задачи на «потерю массы» | 2 | 1 | 1 |
| 9 | Процентное содержание | 2 | 1 | 1 |
| 10 | Процентный раствор | 2 | 1 | 1 |
| 11 | Вклады в банк под проценты | 2 | 1 | 1 |
| 12 | Проценты в жизненных ситуациях | 2 | 1 | 1 |
| 13 | Задачи здоровьесберегающей направленности | 2 | 1 | 1 |
| 14 | Игра «Пентагон» | 2 |
| 2 |
| 15 | Задачи на концентрацию | 4 | 1 | 3 |
| 16 | Задачи на смеси | 3 | 1 | 2 |
| 17 | Задачи на сплавы | 3 | 1 | 2 |
| 18 | Переливание | 3 | 1 | 2 |
| 19 | Растворы | 3 | 1 | 2 |
| 20 | Сушка | 3 | 1 | 2 |
| 21 | Игра «Заработай миллион!» | 2 |
| 2 |
| 22 | Распродажа. Тарифы. Штрафы. | 4 | 1 | 3 |
| 23 | Сложные проценты (цена) | 4 | 1 | 3 |
| 24 | Сложные проценты (банк) | 4 | 1 | 3 |
| 25 | Сложные проценты (рост или убыль населения) | 3 | 1 | 2 |
| 26 | Деловая игра «Математик-бизнесмен» | 2 |
| 2 |
| 27 | Что значит – жить на проценты? | 1 | 1 |
|
| 28 | Проценты в мире профессий | 1 | 1 |
|
| 30 | «Своя игра» | 2 |
| 2 |
| Итого | 68 | 23 | 45 |
Содержание программы
1. Введение. Что такое процент?
Слово процент от латинского слова pro centum, что буквально означает «за сотню» или «со ста». Идея выражения частей целого постоянно в одних и тех же долях, вызванная практическими соображениями, родилась еще в древности у вавилонян. Ряд задач клинописных табличек посвящен исчислению процентов, однако вавилонские ростовщики считали не «со ста», а «с шестидесяти».
Проценты были особенно распространены в Древнем Риме. Римляне называли процентами деньги, которые платил должник заимодавцу за каждую сотню. От римлян проценты перешли к другим народам Европы. Долгое время под процентами понимались исключительно прибыль или убыток на каждые сто рублей. Они применялись только в торговых и денежных сделках. Затем область их применения расширилась, проценты встречаются в хозяйственных и финансовых расчетах, статистике, науке и технике.
Проценты были известны и индийцам еще в V веке. Это закономерно, так как в Индии с давних пор счет ввелся в десятичной системе счисления. В Европе десятичные дроби появились на тысячу лет позже, их ввел бельгийский ученый С. Стевин. В 1584 г. он впервые опубликовал таблицу процентов.
Сейчас процент – это частный вид десятичных дробей, сотая доля целого (принимаемого за единицу). Знак % происходит, как полагают, от итальянского слова cento (сто), которое в процентных расчетах часто писалось сокращенно cto. Отсюда путем дальнейшего упрощения в скорописи буква t превратилась в наклонную черту (/), возник современный символ для обозначения процента. В школьном учебнике «Математика, 5», авторов Н.Я. Виленкина и др. дана еще одна любопытная версия возникновения знака %. Там, в частности, говорится, что этот знак произошел в результате нелепой опечатки, совершенной наборщиком. В 1685 г. в Париже была опубликована книга - руководство по коммерческой арифметике, где по ошибке наборщик вместо cto напечатал %. После этой ошибки многие математики также стали употреблять знак % для обозначения процентов, и постепенно он получил всеобщее признание.
Современная жизнь делает задачи на проценты актуальными, так как сфера практического приложения процентных расчетов расширяется. Вопросы инфляции, повышение цен, рост стоимости акций, снижение покупательской способности касаются каждого человека в нашем обществе. Планирование семейного бюджета, выгодного вложения денег в банки, невозможны без умения производить несложные процентные вычисления.
Сами проценты не дают экономического развития, но их знание помогает в развитии практических способностей, а также умение решать экономические задачи. Обдуманное изучение процентов может способствовать развитию таких навыков как экономичность, расчетливость.
2. Процентные повышения.
Среди всего многообразия текстовых задач часто приходится решать задачи на «процентные повышения».
Теоретические сведения
Определение. Процентом числа называется его сотая часть.
1% = 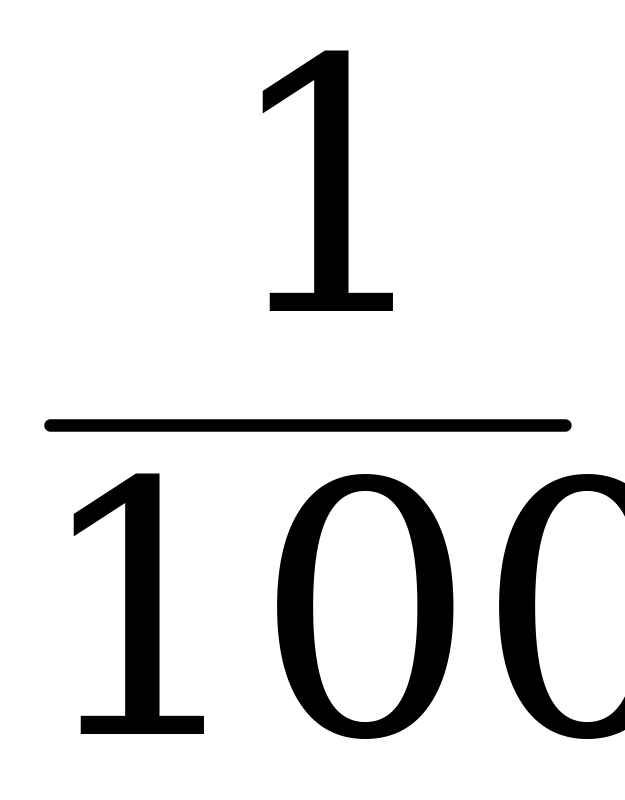 = 0,01
= 0,01
а · р% = b
Решение любых задач на проценты сводится к основным трем действиям с процентами:
Пример: Найти 15% от числа 60.
0,15 · 60 = 9
Ответ: 9.
Пример: Найти число, 12% которого равны 30.
12% неизвестного числа нам известны – это 30. Обозначим неизвестное число за х и найдем его из пропорции:
х – 100%
30 – 12%
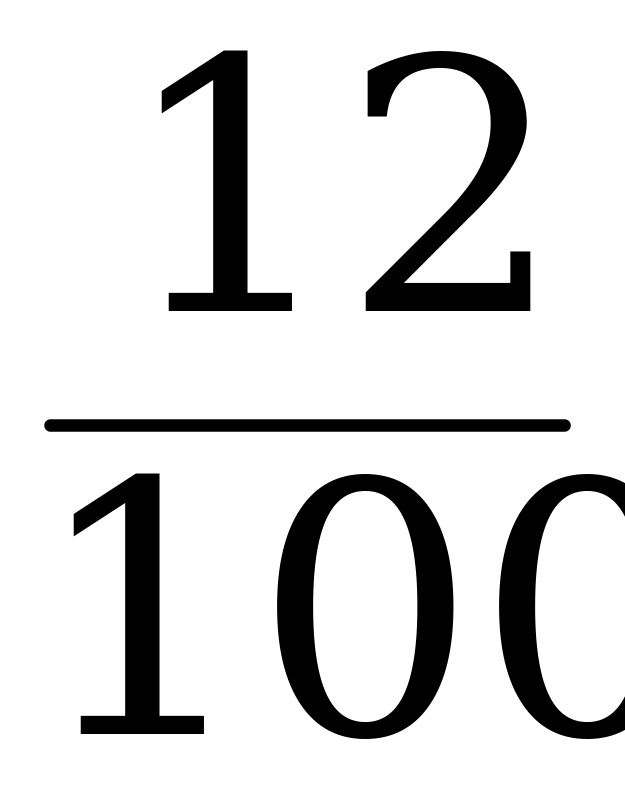 =
=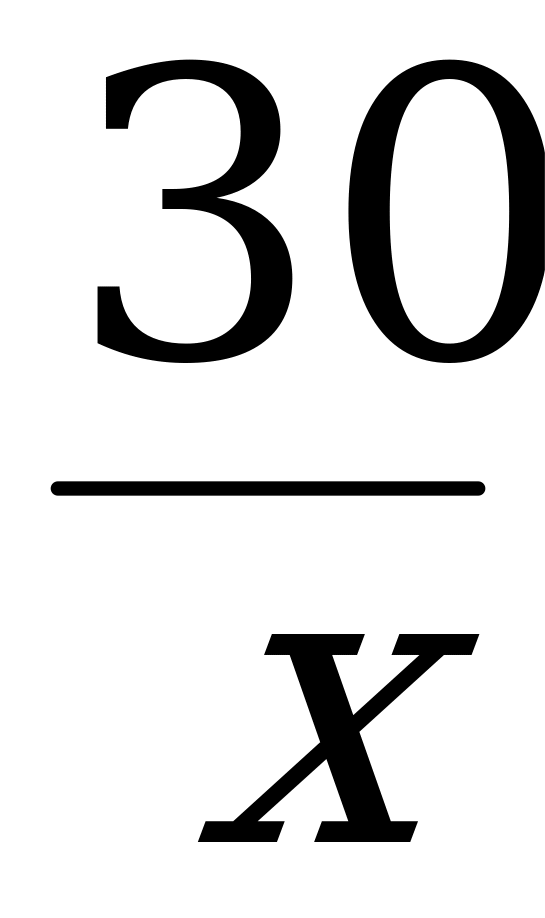 ; х =
; х = 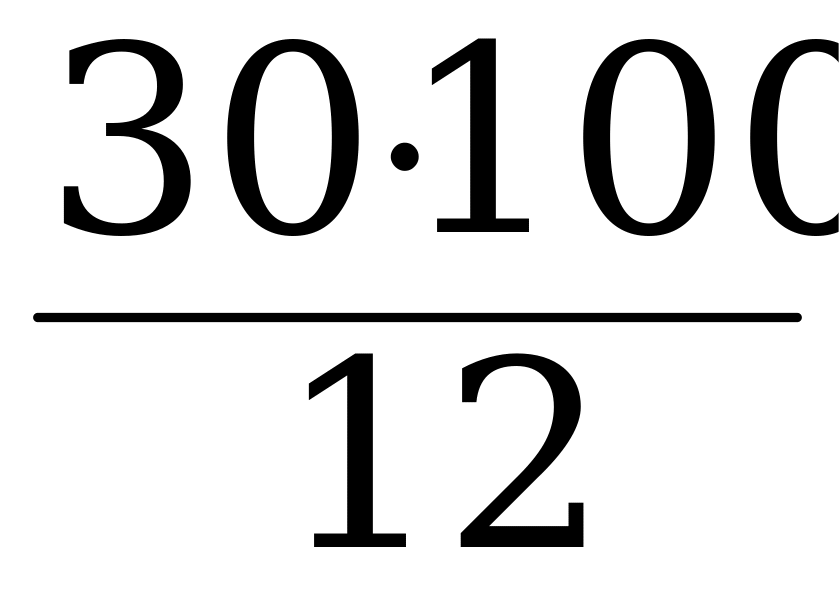 =250
=250
Ответ: 250.
Пример: Сколько процентов составляет 120 от 600?
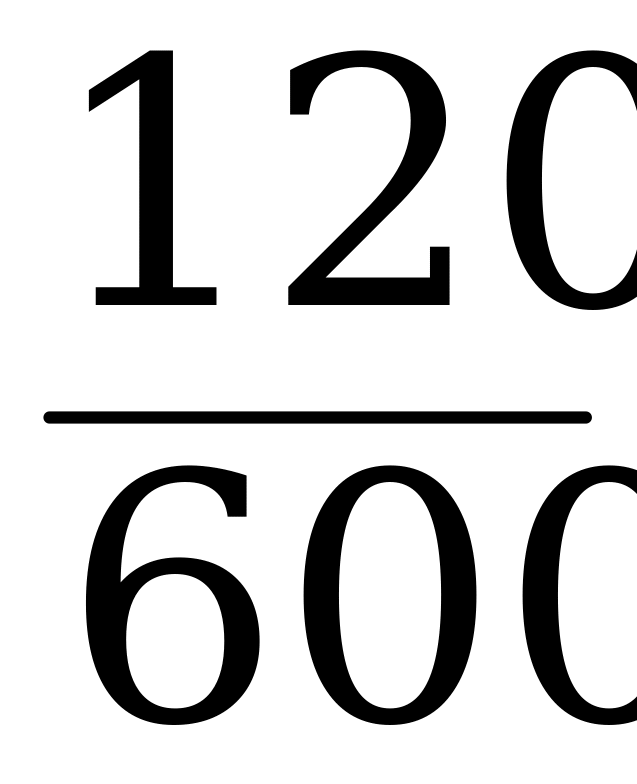 · 100% = 20%
· 100% = 20%
Ответ: 20%.
Формула сложных процентов: А* = А (1+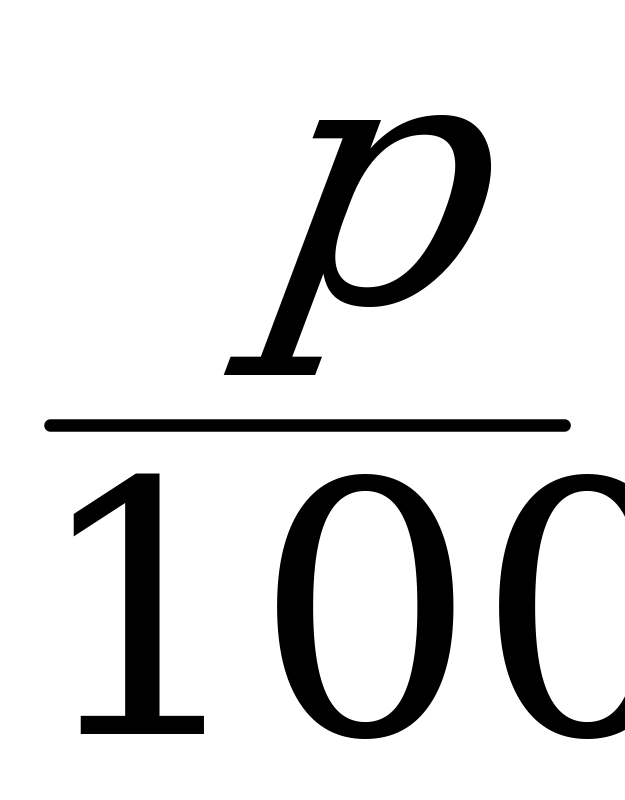 )n
)n
n – количество временных лет;
р – процент за месяц;
А – сумма, положенная в банк.
Задачи:
1. Предприятие уменьшило выпуск продукции на 20%. На сколько процентов необходимо теперь увеличить выпуск продукции, чтобы достигнуть его первоначального уровня.
Решение:
а · 0,8 = b; а = b · 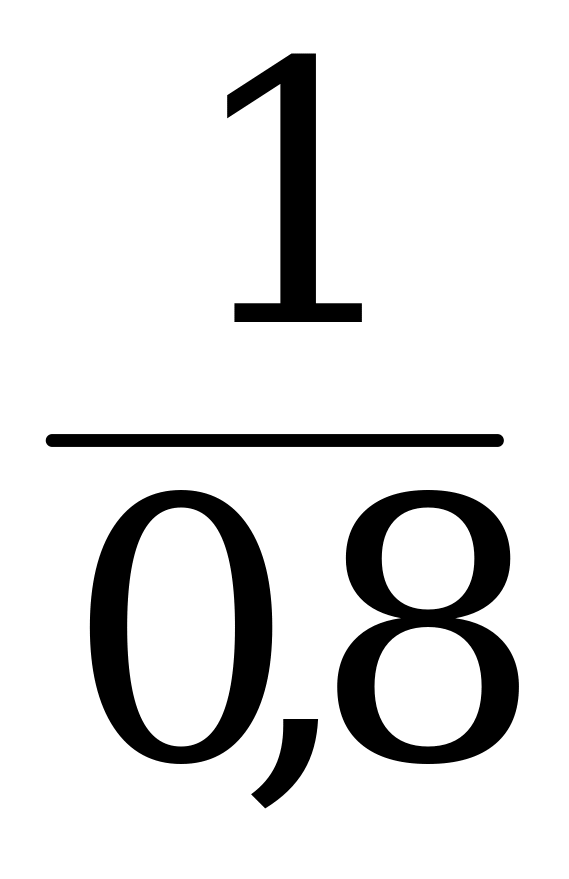 = b · 1,25 ═ Необходимо увеличить на 25%.
= b · 1,25 ═ Необходимо увеличить на 25%.
Ответ: 25%.
2. Вследствие инфляции цены выросли на 25%. Дума потребовала от правительства возвращения цен к прежнему уровню. На сколько для этого должны быть уменьшены цены?
Решение:
а · 1,25 = b; а = b · 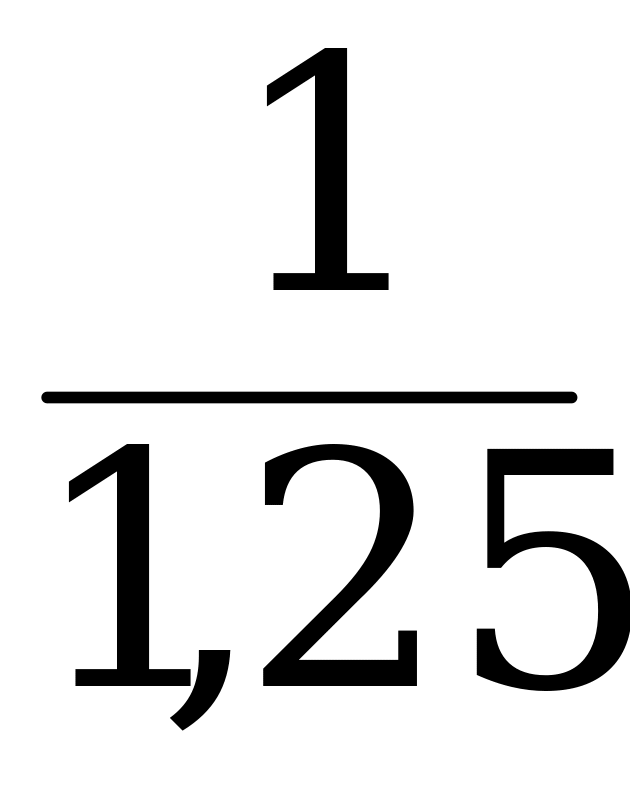 = b · 0,8 ═ Должны быть уменьшены на 20%.
= b · 0,8 ═ Должны быть уменьшены на 20%.
Ответ: 20%.
3. Цену товара сначала повысили на 30%, а затем понизили на 30%. На сколько в итоге изменилась цена?
Решение:
а · 1,3 · 0,7 = b; а · 0,91 = b ═ Изменилась на 9%.
Ответ: 9%.
4. За год стипендия студента увеличилась на 32%. В первом полугодии стипендия увеличилась на 10%. Определите, на сколько процентов увеличилась стипендия во втором полугодии.
Решение:
(а · 1,1) · х = а · 1,32; х = 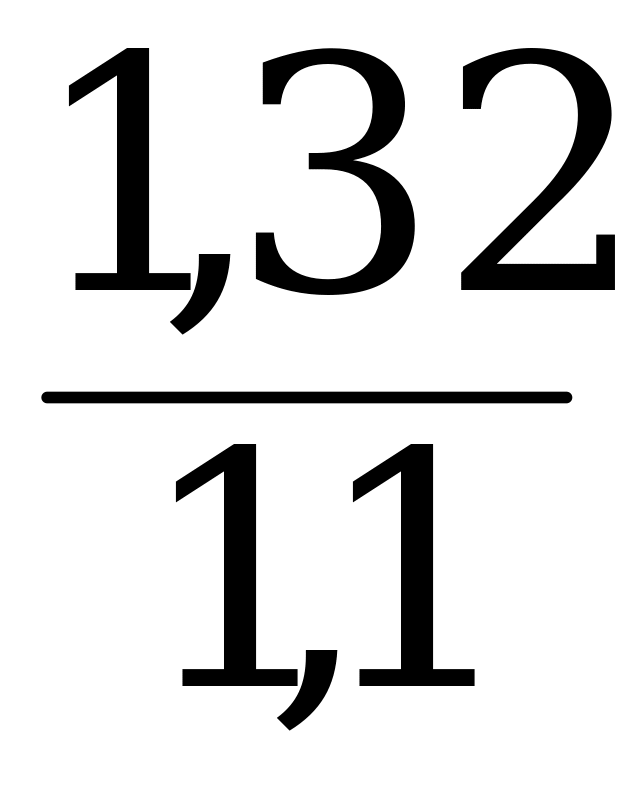 = 1,2 = 120% ═ Второй раз повысили на 20%.
= 1,2 = 120% ═ Второй раз повысили на 20%.
Ответ: 20%.
5. Цена товара после двух повышений цен выросла на 170%, причем первый раз цена повышалась на 80%. На сколько процентов осуществлено второе повышение цены?
Решение:
(а · 1,8) · х = а · 2,7; х = 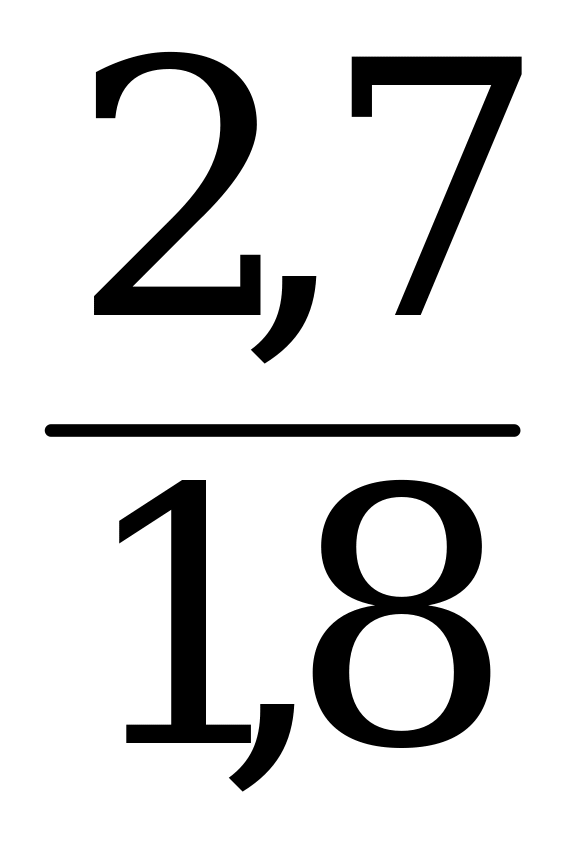 = 1,5 = 150% ═ Второй раз повысили на 50%.
= 1,5 = 150% ═ Второй раз повысили на 50%.
Ответ: 50%.
6. В феврале цена на нефть упала на 10% по сравнению с январской. В марте цена поднялась на 20%. На сколько процентов изменилась мартовская цена по сравнению с январской?
Решение:
а · 0,9 · 1,2 = b; а · 1,08 = b ═ Изменилась на 8%.
Ответ: 8%.
7. Торговая база закупила у изготовителя партию альбомов и поставила ее магазину по оптовой цене, которая на 30% больше цены изготовителя. Магазин установил розничную цену на альбом еще на 20% выше оптовой. При распродаже в конце сезона магазин снизил розничную цену на альбом на 10%. На сколько рублей больше заплатил покупатель по сравнению с ценой изготовителя, если на распродаже он приобрел альбом за 70,2 рубля?
Решение:
а · 1,3 · 1,2 · 0,9 = 70,2; а = 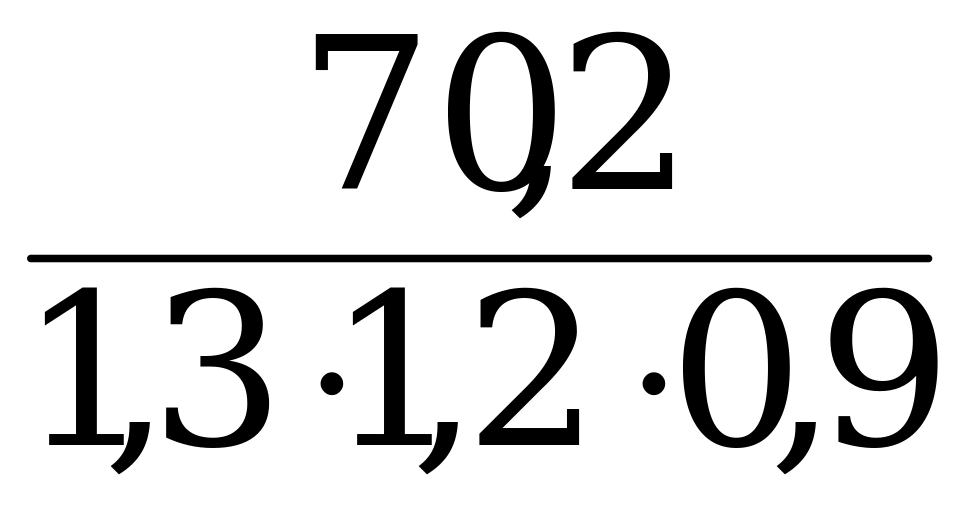 = 50; 70,2 – 50 = 20,2.
= 50; 70,2 – 50 = 20,2.
Ответ: 20,2 р.
8. Ежемесячный доход семьи складывается из зарплаты отца и матери. Зарплату отца увеличили на 40%, а зарплату матери – на 15%. В результате чего семейный доход увеличился на 20%. Сколько процентов от семейного дохода составляла до повышения зарплата матери?
Решение:
р – зарплата отца р · 1,4
– зарплата отца р · 1,4
m - зарплата матери m · 1,15
р + m (р + m) · 1,2
1,4р + 1,15m = 1,2(р + m) : m
1,4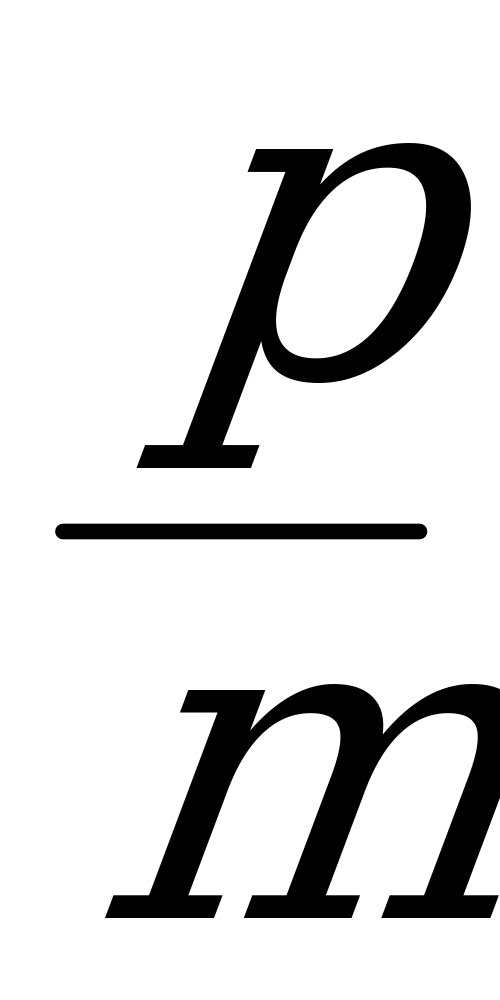 + 1,15 = 1,2
+ 1,15 = 1,2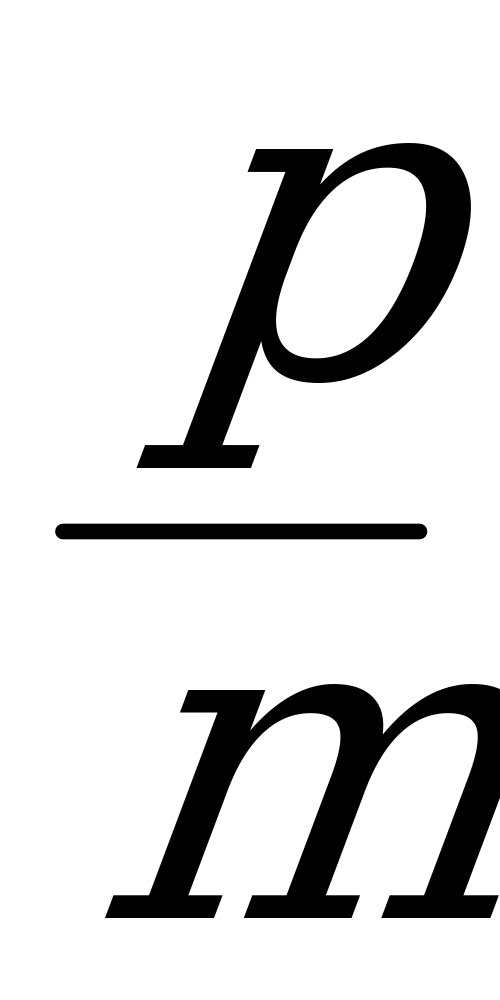 + 1,2
+ 1,2
0,2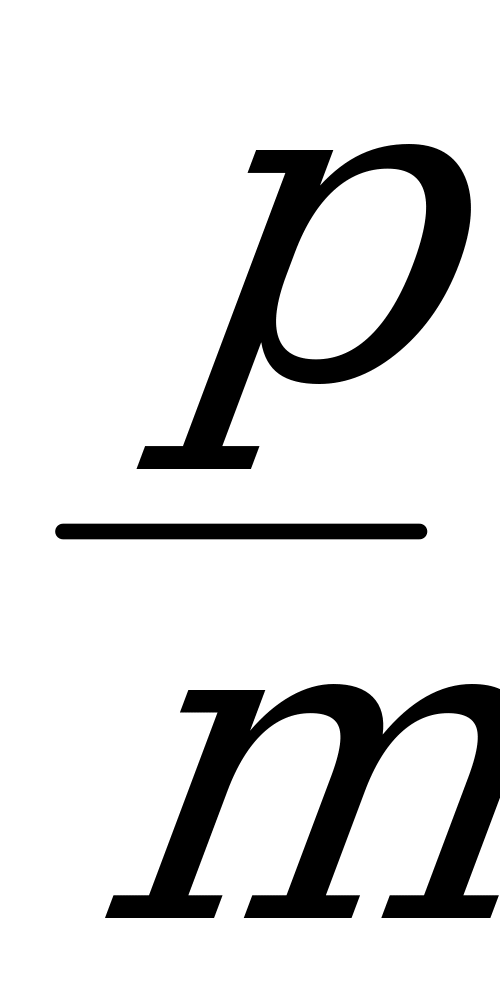 = 0,85
= 0,85
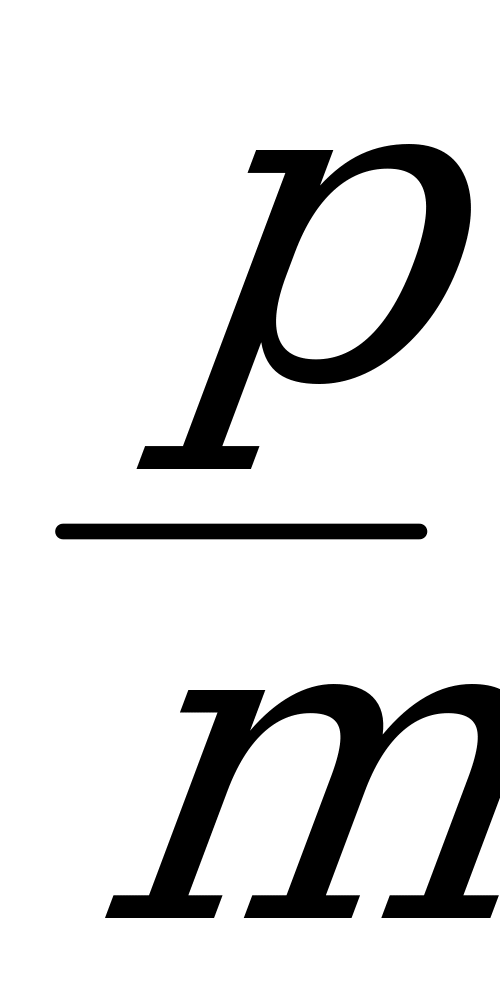
 =
= 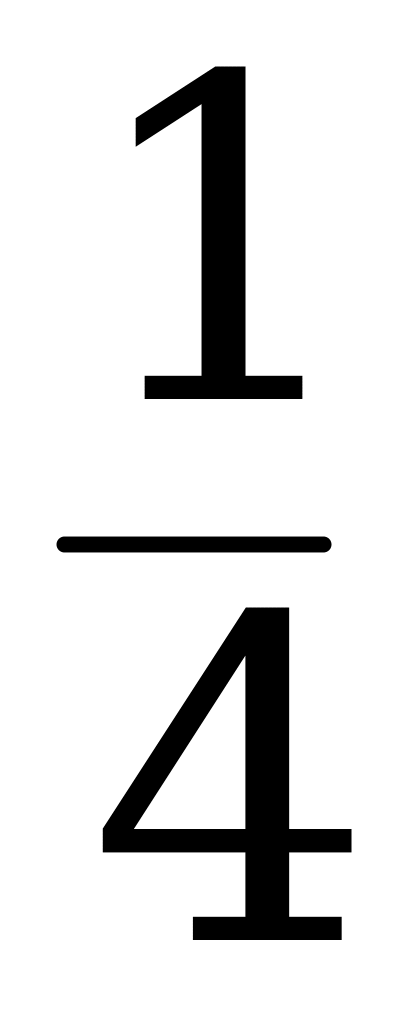 р : m = 1 : 4
р : m = 1 : 4
(р + m) · х = m
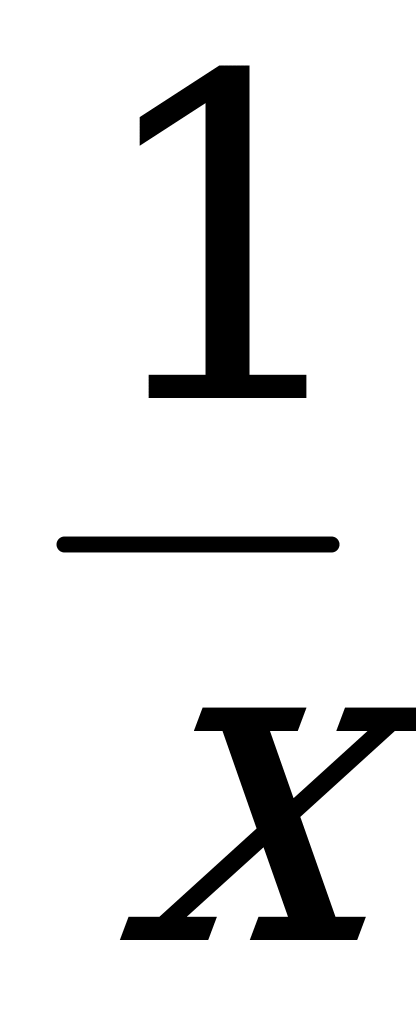 =
= 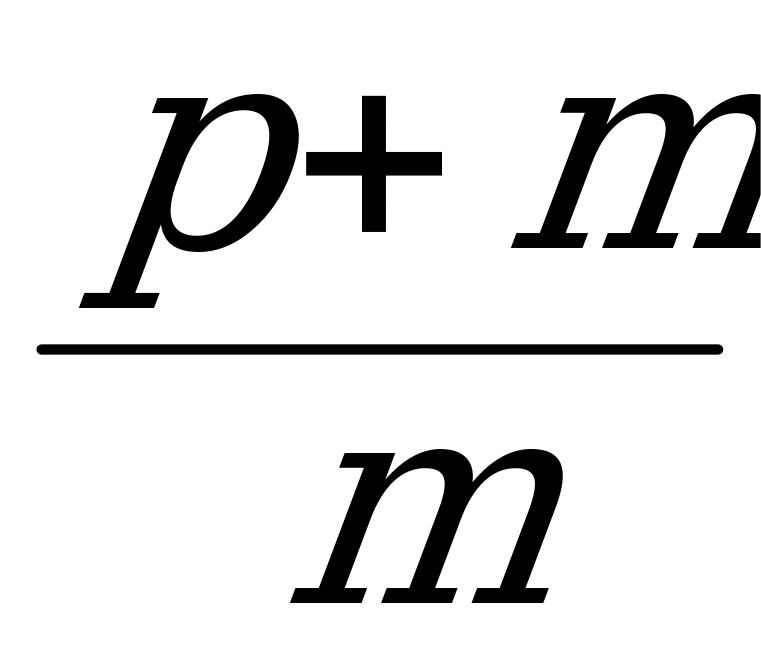
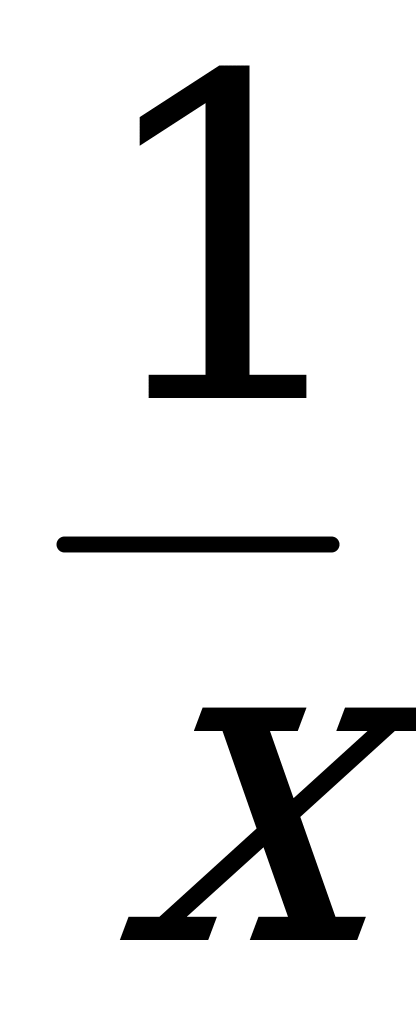 =
= 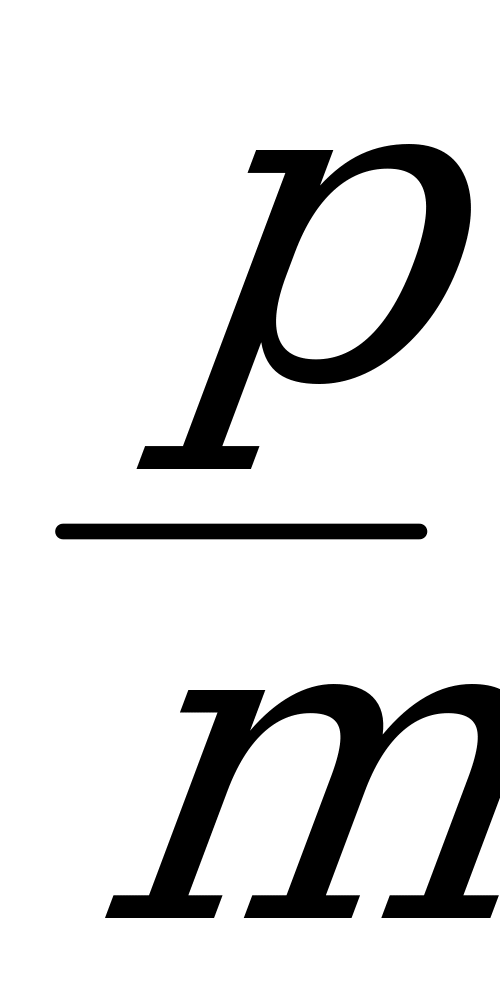 + 1
+ 1
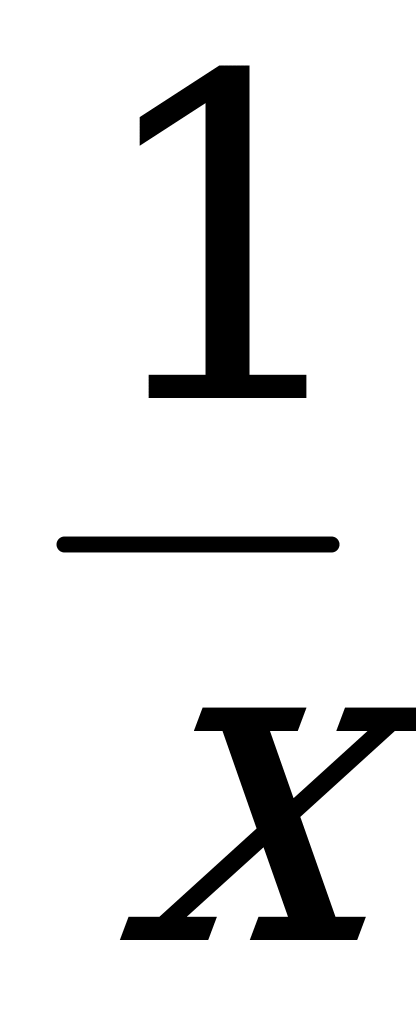 =
= 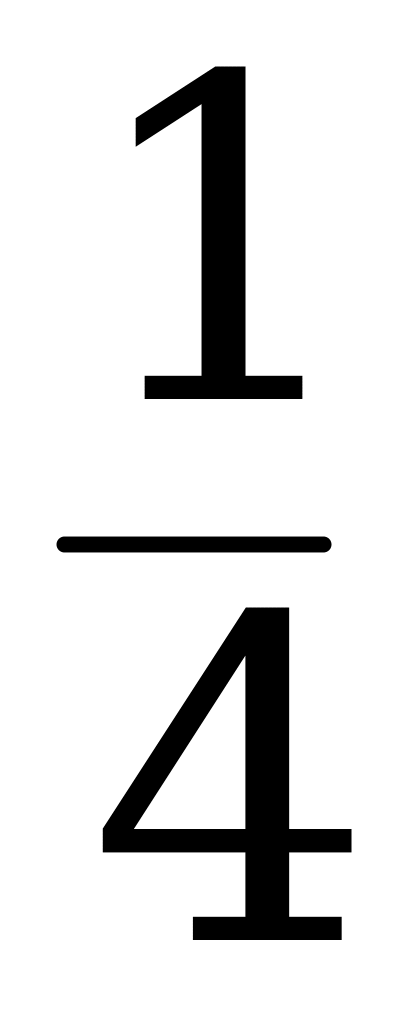 + 1;
+ 1; 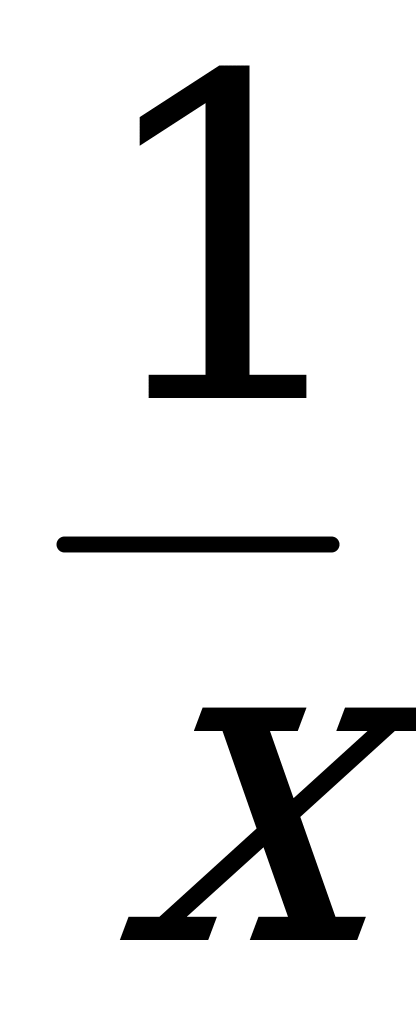 =
= 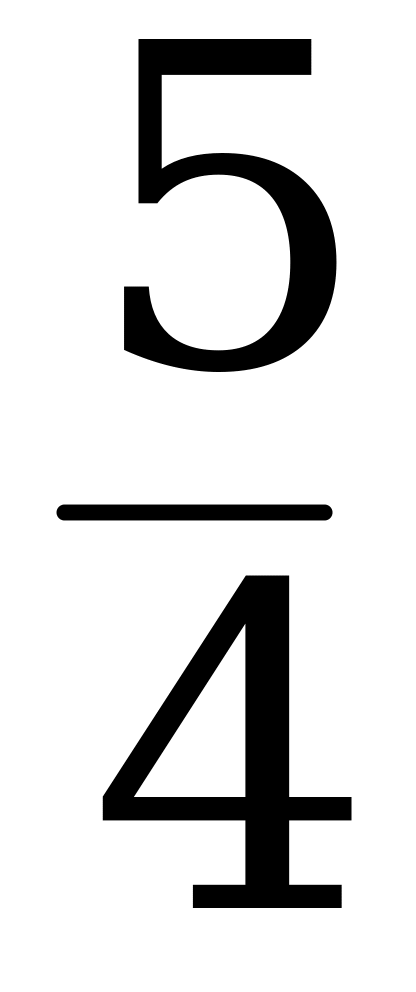 ; х = 0,8
; х = 0,8
Ответ: 80%.
Тест 1. Вследствие инфляции цены выросли на 150%. Дума потребовала от правительства возвращения цен к прежнему уровню. Для этого цены должны быть уменьшены на
1) 60%; 2) 33,(3)%; 3) 66,(6)%; 4) 122,(2)%; 5) 150%.
2. Цену товара сначала повысили на 20%, а затем понизили на 20%. В итоге цена изменилась на
1) 4%; 2) 9%; 3) 16%; 4) 20%; 5) не изменилась.
3. Цена товара после двух повышений цен выросла на 124%, причем первый раз цена повышалась на 60%. Второе повышение цены осуществлено на
1) 64%; 2) 32%; 3) 30%; 4) 40%; 5) 50%.
4. В феврале цена на нефть упала на 12% по сравнению с январской. В марте цена поднялась на 25%. На сколько процентов изменилась мартовская цена по сравнению с январской?
1) 10%; 2) 13%; 3) 8%; 4) 5%; 5) 1,2%.
5. После двух повышений на одно и то же число процентов зарплата выросла на 69%. Каждый раз она повышалась на
1) 29%; 2) 30%; 3) 31%; 4) 34,5%; 5) 33,5%.
6. Если продавец книг получает книгу со скидкой 25% с номинальной цены, а продает ее по номиналу, то процент прибыли продавца составляет
1) 25%; 2) 20%; 3) 36,(6)%; 4) 30%; 5) 33,(3)%.
Ответы:
| №
вопроса | 1 | 2 | 3 | 4 | 5 | 6 |
| №
ответа | 1 | 1 | 4 | 1 | 2 | 5 |
7. Найдите первоначальную сумму вклада (в рублях), если после истечения двух лет она выросла на 304,5 рубля при 3% годовых.
Ответ: 5000 р.
8. Семья состоит из трех человек: отца, матери и сына. Если бы зарплата матери увеличилась вдвое, общий доход семьи вырос бы на 30%. Если бы стипендия сына увеличилась втрое, общий доход семьи вырос бы на 6%. Сколько процентов дохода составляет зарплата отца?
Ответ: 67%.
3. Задачи на «потерю массы».
1. Яблоки при сушке потеряли 84% своей массы. Сколько получится сушеных яблок из 400 кг свежих?
Решение:
400 – 400 · 0,84 = 64 (кг)
Ответ: 64 кг.
2. На базу привезли 100 кг грибов, влажность которых составляла 99%. Через неделю влажность грибов уменьшилась до 98%. Сколько кг стали весить грибы?
Решение:
100 · 0,01 = х · 0,02
х = 50
Ответ: 50 кг.
3. Влажность купленного арбуза составила 99%. В результате длительного хранения влажность снизилась до 98%. Как изменилась влажность арбуза?
Решение:
Свежий арбуз на 99% процентов состоит из жидкости и на 1% - из сухой массы. В результате усушки количество жидкости уменьшилось и составило 98% от новой, также уменьшившейся массы арбуза.
Количество же сухого вещества, оставаясь неизменным, составило 2% от новой массы арбуза. Процентное содержание в арбузе сухого вещества (при неизменной его массе) увеличилось вдвое.
Следовательно, масса арбуза в результате усушки уменьшилась вдвое.
Ответ: Уменьшилась в два раза..
4. Свежие грибы содержали по массе 90% воды, а сухие 12%. Сколько получится сухих грибов из 22 кг свежих?
Решение:
1) 22 . 0,1 = 2,2 (кг) - грибов по массе в свежих грибах;
2) 2,2 : 0,88 = 2,5 (кг) - сухих грибов, получаемых из свежих.
Ответ: 2,5 кг.
5. Сколько кг белых грибов надо собрать для получения 1 кг сушеных, если при обработке свежих грибов остается 50% их массы, а при сушке остается 10% массы обработанных грибов?
Решение:
1кг сушеных грибов – это 10% или 0, 01 часть обработанных,
1 кг : 0,1=10 кг обработанных грибов, что составляет 50% или 0,5 собранных грибов,
10 кг : 0,05=20 кг
Ответ: 20 кг.
4. Процентное содержание. Процентный раствор.
1. Сколько кг соли в 10 кг соленой воды, если процентное содержание соли 15%.
Решение:
10 . 0,15 = 1,5 (кг) соли.
Ответ: 1,5 кг.
Процентное содержание вещества в растворе (например, 15%), иногда называют %-м раствором, например, 15%-й раствор соли.
2. Сплав содержит 10 кг олова и 15 кг цинка. Каково процентное содержание олова и цинка в сплаве?
Решение:
Процентное содержание вещества в сплаве - это часть, которую составляет вес данного вещества от веса всего сплава.
10 + 15 = 25 (кг) - сплав;
10/25 . 100% = 40% - процентное содержание олова в сплаве;
15/25 . 100% = 60% - процентное содержание цинка в сплаве;
Ответ: 40%, 60%.
3. (ЕГЭ, 2004) Имеются два слитка сплава золота с медью. Первый слиток содержит 230 г золота и 20 г меди, а второй слиток – 240 г золота и 60 г меди. От каждого слитка взяли по куску, сплавили их и получили 300 г сплава, в котором оказалось 84 % золота. Определить массу (в граммах) куска, взятого от первого слитка.
Решение:
Определим процентное содержание золота в обоих слитках.
230+20=250(г)-масса 1 слитка,
230/250=0,92 (92%)процентное содержание золота в 1 слитке.
2) 240+60=300(г) –масса 2 слитка,
240/300=0,8 (80%)- процентное содержание золота во 2 слитке.
Пусть х масса куска, взятого от 1 слитка, (300-х)- масса куска, взятого от 2 слитка, получим уравнение 0,92х+0,8(300-х)=0,84*300, откуда х=100.
Ответ: 100г.
4. (ЕГЭ, 2004) Первый сплав серебра и меди содержит 70 г меди, а второй сплав – 210 г серебра и 90 г меди. Взяли 225 г первого сплава и кусок второго сплава, сплавили их и получили 300 г сплава, который содержит 82 % серебра. Сколько граммов серебра содержалось в первом сплаве?
Решение: Пусть х г серебра содержится в 1 сплаве,
тогда 70/(х+70) часть составляет медь в 1 сплаве,
90/(210+90) часть составляет медь во 2 сплаве,
кусок второго сплава 300-225=75г,
тогда получаем уравнение:
225*(70/(х+70))+75*(90/300)=(1-0,82)*300, откуда х=430 г.
Ответ: 430г.
5. (ЕГЭ, 2005) Из сосуда, доверху наполненного 94% -м раствором кислоты, отлили 1,5 л жидкости и долили 1,5 л 70% -го раствора этой же кислоты. После этого в сосуде получился 86% раствор кислоты. Сколько л раствора вмещает сосуд?
Решение:
Пусть х л вмещает сосуд, тогда из условия задачи следует уравнение
0,94(х-1,5)+0,7*1,5=0,86х, откуда х=4,5 л.
Ответ: 4,5 л
6. К 120 г раствора, содержащего 80% соли, добавили 480 г раствора, содержащего 20% той же соли. Сколько процентов соли содержится в получившемся растворе?
Решение:
120 · 0,8 + 480 · 0,2 = (120 + 480) · х
96 + 96 = 600х
х = 0,32 = 32%
Ответ: 32%.
7. Бронза – сплав меди и олова. В древности из бронзы отливали колокола, если в ней содержалось 75% меди. К куску бронзы массой 500 кг и содержащей 72% меди добавили некоторое количество бронзы, содержащей 80% меди, и получили бронзу, необходимую для изготовления колокола. Определите, сколько килограммов 80%-ной бронзы было добавлено?
Решение:
500 · 0,72 + х · 0,8 = (500 + х) · 0,75
360 + 0,8х = 375 + 0,75х
0,8х – 0,75х = 375 - 360
х = 300
Ответ: 300 кг.
8. Смешивается некоторое количество 72 %-го раствора кислоты и некоторое количество 58 %-го раствора кислоты и в результате получается 62 %-ный раствор. Если бы каждого раствора было взято на 15 л больше, то получился бы 63,25 %-ный раствор. Сколько литров каждого раствора было взято первоначально для составления смеси?
Решение:
Пусть х л было взято первоначально для составления смеси первого раствора, у л – второго раствора. Тогда
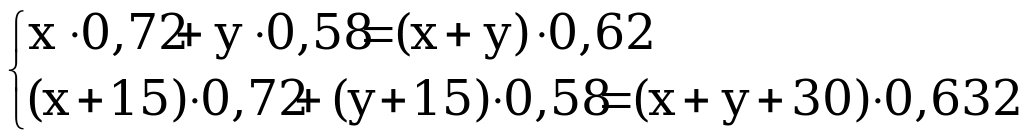
х = 12, у = 30.
Ответ: 12 л, 30л.
Дополнительные задачи
1. Имеется 2 сплава, в одном из которых содержится 40%, а в другом 20% серебра. Сколько кг второго сплава нужно добавить к 20 кг первого, чтобы после сплавления вместе получить сплав, содержащий 32% серебра?
Решение:
Пусть к 20 кг первого сплава нужно добавить х кг второго сплава. Тогда получим (20 + х) кг нового сплава. В 20 кг первого сплава содержится 0,4 . 20 = 8 (кг) серебра, в х кг второго сплава содержится 0,2х кг серебра, а в (20+х) кг нового сплава содержится 0,32 . (20+х) кг серебра. Составим уравнение:
8 + 0,2х = 0,32 . (20 +х);
х = 13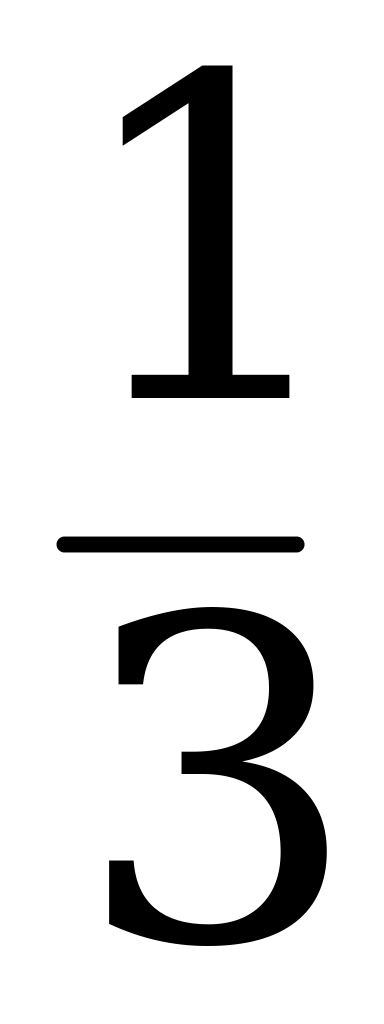 .
.
Ответ: 13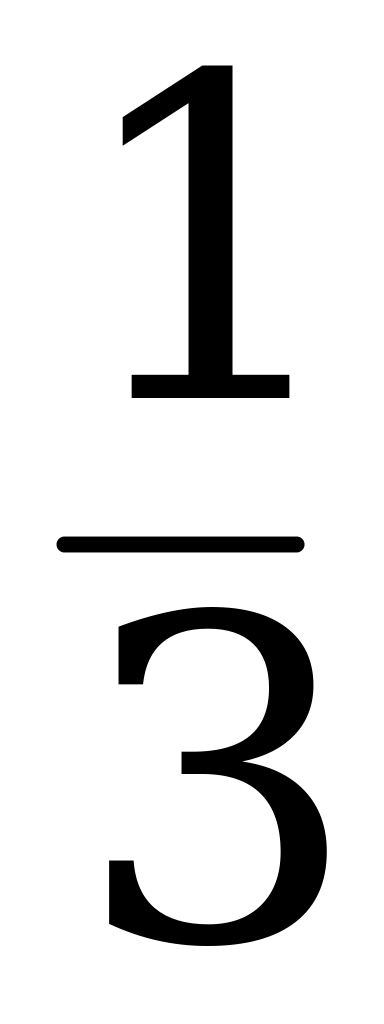 кг второго сплава нужно добавить к 20 кг первого, чтобы получить сплав, содержащий 32% серебра.
кг второго сплава нужно добавить к 20 кг первого, чтобы получить сплав, содержащий 32% серебра.
2. К 15 л 10%-ного раствора соли добавили 5%-ный раствор соли и получили 8%-ный раствор. Какое количество литров 5%-ного раствора добавили?
Решение:
Пусть добавили х л 5%-ного раствора соли. Тогда нового раствора стало (15 + х) л, в котором содержится 0,8 . (15 + х) л соли. В 15 л 10%-ного раствора содержится 15 . 0,1 = 1,5 (л) соли, в х л 5%-ного раствора содержится 0,05х (л) соли. Составим уравнение.
1,5 + 0,05х = 0,08 . (15 + х);
х = 10.
Ответ: добавили 10 л 5%-ного раствора.
5. Вклады в банк под проценты.
В банк были сделаны 3 вклада на 3 различных счета. На первый счет положили 1000 рублей под 8% годовых. На второй счет положили 2000 рублей под 6% годовых. На третий счет положили 3000 рублей под 4% годовых.
1. Сколько можно снять денег по процентам со всех трех вкладов:
- через год (А: 300, Б: 320, В: 360, Г: 400);
- через 6 месяцев (А: 150, Б: 160, В: 180, Г: 200).
2. Чтобы купить сумку по цене 365 рублей, хватит ли денег, накопленных по процентам за 18 месяцев:
а) на каком-нибудь из счетов;
б) на 1 и 2 счетах;
в) на 1 и 3 счетах;
г) на 2 и 3 счетах;
д) на всех трех счетах.
3. Если появится необходимость через год снять 1000 рублей, то с какого счета выгоднее снять деньги:
а) с 1 счета;
б) со 2 счета;
в) с 3 счета;
г) с 1 и 2 счетов пополам;
д) с 1 и 3 счетов пополам;
е) с 2 и 3 счетов пополам;
ж) с каждого из счетов по трети суммы.
4. Что выгоднее:
- оставить все деньги на своих счетах или переложить их все в один из банков (в который)?
а) оставить;
б) в первый;
в) во второй;
г) в третий;
д) все равно;
- оставить деньги на своих счетах или переложить их все во второй банк?
а) оставить; б) переложить; в) все равно.
5. Инфляция составляет 5% в год. Что выгоднее:
а) оставить все деньги на своих счетах;
б) перевести все деньги в 1 банк;
в) перевести все деньги во 2 банк;
г) перевести все деньги в 3 банк;
д) снять деньги со всех счетов;
е) все равно.
Задачи:
1. Сберегательный банк в конце года начисляет 3% к сумме, находившейся на счету. На сколько рублей увеличится первоначальный вклад в 1000 рублей через 2 года?
Решение:
А* = 1000(1 + 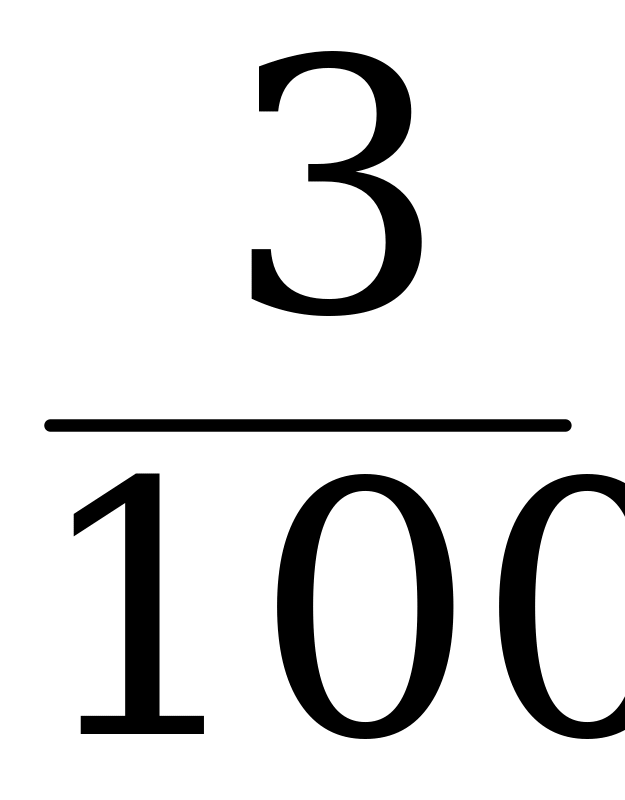 )²; А* = 1060,9 р.; 1060,9 – 1000 = 60,9 р.
)²; А* = 1060,9 р.; 1060,9 – 1000 = 60,9 р.
Ответ: 60,9 р.
2. Вкладчик хочет вложить в банк деньги на 20% годовых, и в течение двух лет не пополнять и не снимать с него. Сколько рублей надо положить вкладчику, чтобы через два года вложенная им сумма увеличилась на 7920 рублей.
Решение:
А + 7920 = А(1 + 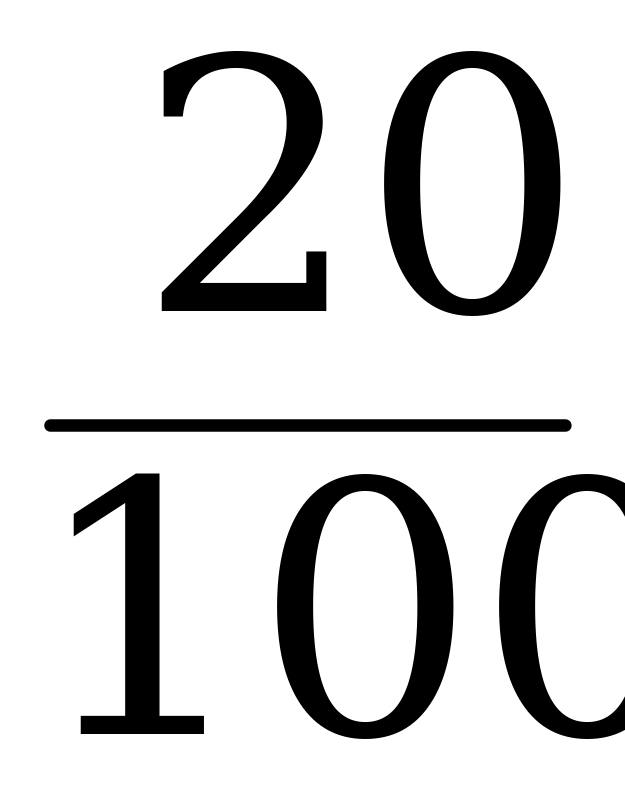 )²; А = 18000 р.
)²; А = 18000 р.
Ответ: 18000 р.
Расчетные задачи по теме "Проценты".
1. Найти 14% от 84.
2. Найти число, если 12% его составляют 9,03.
3. Цена товара 64 руб. После снижения цен товар стал стоить 57 руб. На сколько процентов снижена цена?
4. При продаже товара за 1548 руб получено 20% прибыли. Определить себестоимость товара.
5. Свежие фрукты содержали 72%, а сухие - 20%. Сколько сухих фруктов получится из 20 кг свежих?
6. Кусок сплава меди и олова весом 12 кг содержит 45% меди. Сколько олова надо добавить к этому куску, чтобы в новом сплаве было 40% меди?
7. Имеется лом стали двух сортов с содержанием никеля в 5% и 40%. Сколько нужно взять каждого из этих сортов, чтобы получить 140 т стали с содержанием никеля в 30%?
8. Сколько чистого спирта надо добавить к 735 г 16%-ного раствора йода в спирте, чтобы получить 10%-ный раствор?
9. Сбербанк начисляет по вкладам ежегодно 110%. Вкладчик внес в сбербанк 150 тыс. руб. Какой будет сумма вклада через 2 года?
10. Площадь прямоугольника равна 100 см2. Одна сторона прямоугольника уменьшилась на 16,4%, вторая увеличилась на 25%. Найти площадь нового прямоугольника.
Ответы:
1) 11,76
76,25
10,94%
1290
7
1,5
40; 100
441
661500
104,5.
Задачи для самостоятельного решения.
1. Имеется 2 сплава, в одном из которых содержится 40%, а в другом 20% серебра. Cколько кг второго сплава нужно добавить к 20 кг первого, чтобы после сплавления вместе получить сплав, содержащий 32% серебра?
2. Имеется 2 сплава, в одном из которых содержится 20%, а в другом 30% олова. Сколько нужно взять первого и второго сплавов, чтобы после их сплавления вместе получить 10 кг нового сплава, содержащего 27% олова?
3. Имеется 2 сплава, в одном из которых содержится 10%, а в другом 20% меди. Сколько нужно взять первого и второго сплавов, чтобы после их сплавления вместе получить 15 кг нового сплава, содержащего 14% меди?
4. Имеется 2 сплава, в одном из которых содержится 30%, а в другом 50% золота. Cколько кг второго сплава нужно добавить к 10 кг первого, чтобы после сплавления вместе получить сплав, содержащий 42% серебра?
5. Сплав золота и серебра содержит 20% золота. Какую массу сплава и какую массу чистого золота нужно взять для получения 80 кг нового сплава, содержащего 50% золота?
6. Кусок железа с медью массой в 30 кг содержит 45% железа. Какую массу меди нужно добавить к этому куску, чтобы полученный новый сплав содержал 30% железа.
7. Сплав олова и свинца содержит 40% олова. Какую массу сплава и какую массу чистого свинца нужно взять для получения 40 кг нового сплава, содержащего 10% олова?
Ответы:
13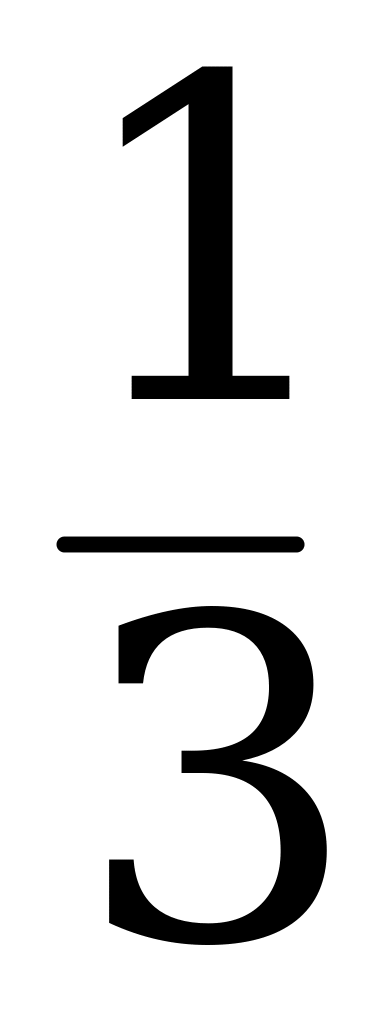 .
.
3; 7.
9; 6.
15.
50; 30.
15.
10; 30.
Список литературы
1. Сборник задач по математике для поступающих в вузы: Учеб. пособие / В.К. Егерев, В.В. Зайцев, Б.А. Кордемский и др.; Под ред. М.И. Сканави. - 6-е изд. – М.: Издательский Дом ОНИКС: Альянс-В, 2000.
2. Федосеенко В.М., Федосеенко О.В. Математика для старших классов за 1 год: Суперпрограмма XXI века. – М.: РИПОЛ классик, 2005.
3. Иванов А.П. Тематические тесты для систематизации знаний по математике. Ч. 1: Учеб. пособие. Изд. 3-е, испр. и доп. – М: Физматкнига, 2004.
4. Креславская О.А. Математика: ЕГЭ. Сдаем без проблем! / О.А. Креславская, В.В. Крылов, В.И. Снегурова, В.Е. Ярмолюк. – М.: Эксмо, 2007.
5. Лурье М.В., Александров Б.И. Задачи на составление уравнений: Учеб. руководство. – 3-е изд., перераб. – М.: Наука. Гл. ред. физ.-мат. лит., 1990.








 – зарплата отца р · 1,4
– зарплата отца р · 1,4 =
= 









