Проценты в нашей жизни

Проценты в нашей жизни

"Свяжем школу с жизнью!"

Когда-нибудь это у нас должно получиться!"

• Развитие рыночных отношений создало объективную потребность создания образовательной среды для формирования экономической культуры подрастающего поколения. Финансовая математика становится неотъемлемой частью общего образования.

• Школьные курсы математики почти полностью игнорируют многие элементарные, но очень важные для повседневной жизни приемы анализа экономических процессов.

• Одной из таких тем является тема «Проценты». Эта тема является универсальной. Она связывает между собой многие точные и естественные науки, бытовые и производственные сферы.

• Понятие «проценты» буквально вошло в нашу жизнь, оно атакует нас в пору утверждения рыночных отношений в экономике, в пору банкротств, инфляций, финансовых кризисов.

• Тема «Проценты» изучается в 6 классе, когда учащиеся в силу возрастных особенностей еще не могут получить полноценное представление о процентах, об их роли в повседневной жизни. На дальнейших этапах обучения возвращения к данной теме не предусматривается, хотя задачи на проценты включены в материал итоговой аттестации за курс основной и средней школы, в конкурсные экзамены.

• Понимание процентов и умение производить процентные вычисления в настоящее время необходимы каждому человеку. Очень велико прикладное значение этой темы. Она затрагивает финансовую, демографическую, экологическую. Социологическую и другие сферы.

• Проценты творят чудеса. Зная их, бедный может стать богатым. Обманутый вчера в торговой сделке покупатель, сегодня обоснованно требует процент торговой скидки. Вкладчик сбережений учится жить на проценты, грамотно размещая деньги в прибыльное дело.

Место урока в программе

• Данный урок предлагается провести в девятом классе в рамках темы «Решение текстовых задач» или в одиннадцатом классе при подготовке к итоговой аттестации в разделе «Повторение». Из всех задач на проценты на данном уроке (спаренном) я предлагаю рассмотреть проценты в банковских расчетах.

Цель урока

1.Сформировать понимание необходимости знаний процентных вычислений для решения большого круга задач

2.Способствовать интеллектуальному развитию учащихся, формированию качеств мышления, характерных для математической деятельности и необходимых человеку для общей социальной ориентации и решения практических задач.

Задачи урока

• Сформировать умение производить различные процентные вычисления
• Научить решать основные задачи на проценты, применять формулы простого и сложного процентного роста
• Прививать учащимся основы экономической грамотности

Ход урока

• Повторение ранее известных сведений о процентах
• Рассмотрение основных типов задач на проценты
• Решение задач, связанных с банковскими расчетами
• Самостоятельная работа

Слово « процент » происходит от латинских слов pro centum , что буквально означает « со ста ».

Историческая справка

Знак % произошел, благодаря опечатке. В рукописях pro centum часто заменяли словом « cento » ( сто) и писали его сокращенно – cto . В 1685 году в Париже была напечатана книга – руководство по коммерческой арифметике, где по ошибке наборщик вместо cto набрал % .

После этой ошибки математики стали употреблять знак % для обозначения процентов.

ТЕКСТОВЫЕ ЗАДАЧИ НА ПРОЦЕНТЫ

• Эта тема стала весьма популярной на вступительных экзаменах в последние годы. Здесь нужно запомнить:
• 1) процент величины — одна сотая часть этой величины;
• 2) если число a составляет p % от числа b , то эти числа связаны равенством a = b :100* p (или a =0,01 b * p );
• 3) если число a увеличено на p %, то оно увеличено в раз, а если уменьшено на q % , то оно уменьшено в раз.

Основные задачи на проценты

• Нахождение процентов от числа
• Нахождение числа по его процентам
• Процентное отношение двух чисел
• Вычисление простых и сложных процентов

Экономико-математический кроссворд «Проценты и банк»

По горизонтали:

2 . Учреждение, хранящее денежные средства.

4 . Нецелое число.

5 . Сотая часть числа.

6 . Страна, в которой впервые появились банковские учреждения.

По вертикали:

1 . Денежные вклады в банк.

3 . Ссуда.

4 . Синоним слова «часть».

1.

2.

3.

4.

5.

6.

Нахождение процентов от числа

• Чтобы найти а % от в надо в*0,01а или в:100*а

Например:

• Найдите двумя способами 5% от400, 10% от 270
• Яблоки при сушке теряют 845 своей массы. Сколько сушеных яблок получится из 300 кг свежих?

Нахождение числа по его процентам

• Если известно. Что а % числа х равно в, то х=в:о,01а или х=в:а*100

Например:

• Найдите двумя способами число, 40% которого равны 320,число 8% которого равны 400
• Из свежих слив получается 355 сушеных. Сколько надо взять свежих слив, чтобы получить 140 кг сушеных?

Процентное отношение двух чисел

• Чтобы найти процентное отношение двух чисел, надо отношение этих чисел умножить на 100%: а:в*100%

Например:

Сколько процентов составляет 150 от 600, 29 от 100?

Из 800 обследованных школьников 160 оказались с пониженным зрением. Какой процент составляют школьники с пониженным зрением?

Анаграмма

разгадайте зашифрованные слова и уберите лишнее слово, не подходящее по смыслу:

1) ТОП + ДИЕЗ;

2) РЕ + ТИК + Д;

3) Ц + ТОН + РЕ + П;

4) ПО + ПИР + Я + ОР + Ц.

Ответ: 1) ДЕПОЗИТ; 2) КРЕДИТ;

3) ПРОЦЕНТ; 4) ПРОПОРЦИЯ.

Тест

1. (1 балл) Процент - это:

• А)тысячная часть числа;
• Б)сотая часть числа;                      
• В)десятая часть числа

2. (1 балл) Дробь 1 /5 равна

• А) 20%
• Б) 30%
• В) 50%

Тест:

3. (2 балла) 30% от числа 800 равно

• А) 24
• Б) 240
• В) 2400

4. (2 балла) У мамы 250 р. На покупку книги она истратила 10% этой суммы. Мама истратила: А) 2,5 р. Б) 25 р. В) 5 р.

5. (1 балл) Чтобы найти 25% от числа, надо это число:

• А) умножить на 25;
•     Б) разделить на 0,25; 
•     В) умножить на 0,25;   

6. (1 балл) 1% дециметра называют: А) миллиметр Б) сантиметр В) метр

7. (3 балла) В магазин привезли 25 ц. фруктов. Яблоки составляют 60%, а груши 20% от общего количества фруктов. Всего в магазин яблок и груш привезли:

• А) 20 ц.
• Б) 5 ц.
• В) 15 ц.

8. Банк начисляет 40% годовых. Какую сумму надо положить в банк, чтобы получить через год 3,5 тыс. руб.?

• а) 2,1 тыс. руб.;
• б) 87 руб. 50 коп.;
• в) 2,5 тыс. руб.

Устные задачи

• Какую сумму следует положить в банк, выплачивающий 25% годовых, чтобы по истечении года получить 1000руб.?

• Вкладчик положил на счет в банк 3000руб. и написал поручение ежемесячно перечислять 5% этой суммы за квартплату. Сколько денег останется на его счете через 8 месяцев?

• При выдаче наличных рублей по дорожным чекам AMERICAN EXPRESS выписываемых в долларах, банк удерживает 2% в качестве комиссионных. Какова будет сумма в рублях, если клиент заказал 400$ и курс обмена 30,4руб. в месяц ?

• Сбербанк начисляет по вкладам ежегодно 110%. Вкладчик внес в сбербанк 150 тыс. руб. Какой будет сумма вклада через 2 года?

Простой и сложный процентный рост

• Проценты могут рассчитываться по –разному в зависимости от вида, характера и срока ссуды. Одно из основных отличий заключается в выборе исходной базы для начисления процентов.
• Если проценты начисляются по отношению к исходной сумме, то это простой процентный рост.
• Если проценты начисляются по отношению к величине, включающей первоначальную сумму и проценты, начисленные за прошедший период, то это сложный процентный рост.

Условные обозначения:

P – первоначальная сумма

i – ставка простого процента

I – проценты за весь срок

T – срок ссуды

S – сумма к концу срока

t – период начисления

n=T/t – количество периодов начисления

P*I – начисленные проценты за один период начисления

Формула простых процентов

• S = P + P*i*n = P* (1 + i*n)

Множитель (1 + i*n) называется множителем наращения простых процентов.

Рассмотрим пример:

Вы берете в банке ссуду 100000 рублей на два года под 16%. Необходимо определить какую сумму вы вернете банку к концу срока.

P=100000, T=2, i=16, n=2:1=2

Тогда I=P*i*n=100000*0,16*2=32000

S=P+I=100000+32000=132000

Таким образом, при исчислении по методу простых процентов при ставке 16% годовых, с суммы в 100000 рублей вы должны будете вернуть банку 132000 рублей.

Сложный процентный рост

• В долгосрочных финансовых операциях часто применяется не простые, а сложные проценты. С этим методом хорошо знакомы те, кто хранит свои вклады в сберегательном банке , иными словами дает банку ссуду под сложный процент. Как правило, сберегательные счета во всех коммерческих и государственных банках основаны на принципах сложных процентов.

Формула сложного процента

• Проценты, полученные за год прибавляются к первоначальной сумме вклада, и в следующем году проценты начисляются уже на новую сумму, и так каждый год.

В принятых нами обозначениях сумма, образовавшаяся к концу срока будет рассчитываться по формуле

S=P*(1+i) *(1+i)*… *(1+i) = P*(1+i) ⁿ

Эта формула означает, что рост первоначальной суммы по сложным процентам – это процесс, развивающийся в геометрической прогрессии, первый член которой равен P , а знаменатель (1+i) . Величина (1+i) ⁿ - это множитель наращения сложных процентов

Рассмотрим пример:

• Вы хотите узнать во сколько раз вырастет Ваш вклад в сберегательный банк, положенный на 10 лет под 8% годовых. По таблице сложных процентов находим множитель наращения равный 2,2. Это означает, что ваш вклад увеличится в 2,2 раза. Формула сложного процента предполагает, что ставка процента на протяжении всего срока не меняется.

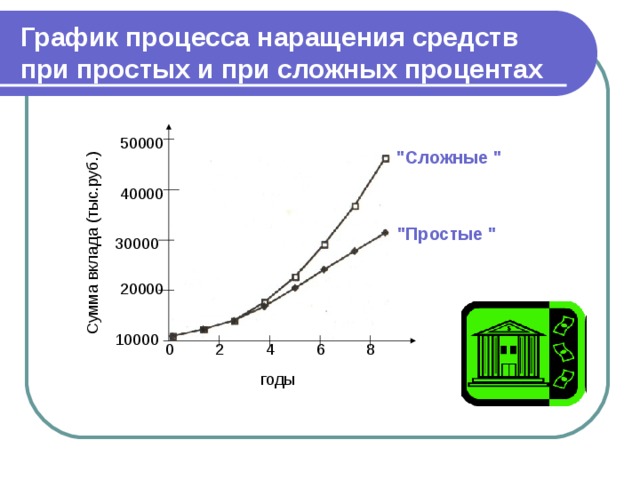
Сумма вклада (тыс.руб.)

График процесса наращения средств при простых и при сложных процентах

50000

"Сложные "

40000

"Простые "

30000

20000

10000

8

6

4

2

0

годы

Старинные задачи на проценты

• Задача 1 . Один небогатый римлянин взял в долг у заимодавца 50 сестринциев. Заимодавец поставил условие: "Ты вернешь мне в установленный срок 50 сестринциев и еще 20% от этой суммы". Сколько сестринциев должен отдать небогатый римлянин заимодавцу?

Задачи на проценты (по материалам ЕГЭ)

• Задача 4. ( из данных сберегательного банка России ) Вкладчик положил некоторую сумму на вклад «Молодежный» в сбербанк России. Через два года вклад достиг 2809 рублей. Каков был первоначальный вклад при 6% годовых?
• Решение: Пусть х рублей первоначальный вклад.

S о → S о∙(1+6∙0,01) → S о∙(1+6∙0,01) ∙(1+6∙0,01)

х ∙(1+0,06) ² =2809

1,06 ² х =2809

1,1236 х =2809

х =2500

Ответ: первоначальный вклад составлял 2500 рублей.

• Банк предлагает вклад «студенческий». По этому вкладу сумма, имеющаяся на 1 января, ежегодно увеличивается на одно и то же число процентов. Вкладчик положил 1 января 1000 рублей и в течение 2 лет не производил со своим вкладом никаких операций. В результате вложенная им сумма увеличилась до 1210 рублей. На сколько процентов ежегодно увеличивается сумма денег, положенная на этот вклад?

• Решение:

Пусть на i % ежегодно увеличивается сумма денег. Положенная на «студенческий» вклад.

S=1210, P=1000, n=2

По формуле сложных процентов получаем: 1210=1000*(1+ i ) ²

(1+ i ) ² =1,21

1+ i =1,1

i =0,1

• Ответ: процентная ставка составляет 10%.

Банк начисляет 40% годовых. Какую сумму надо положить в банк, чтобы получить через год 3,5 тыс. руб.?

Варианты ответа:а) 2,1 тыс. руб.; б) 87,5руб. в) 2,5 тыс. руб.

Правильный ответ: в). Пусть Вы положили X руб. Через год на Вашем счету

Задачи на проценты (по материалам конкурсных экзаменов)

• Банк выплачивает 3% годовых. Через сколько лет первоначальная сумма удвоится?
• Пусть это произойдет через n лет. Тогда P*(1+ о,03 ) ⁿ =2Р

n = log 1,03 2 ≈23

Ответ: через 23 года.

МИФИ, 2001г.

• На счет, который вкладчик имел вначале первого года, банк начисляет в конце этого года р % годовых, а на тот счет, который вкладчик имел вначале второго года, банк начисляет в конце этого года r % годовых , при чем p + r=140 .Вкладчик положил на счет вначале первого года некоторую сумму и снял со счета в конце года (после начисления процентов) пятую часть положенной суммы. При каком р счет вкладчика в конце года окажется максимально возможным?
• Ответ: 80%

Задачи на проценты (по материалам олимпиад)

А.В.Фарков «Математические олимпиады в школе». (Задача 8.32)

М.В.ломоносов тратил одну денежку на хлеб и квас. Когда цены выросли на 20%. На ту же денежку он приобретал пол хлеба и квас. Хватит ли той же денежки хотя бы на квас, если цены еще вырастут на 20%?