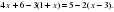Результаты освоения учебного курса математики 6 класса
Контроль предметных результатов
Контроль результатов обучения - важная часть процесса обучения. Его задача заключается в том, чтобы определить, в какой мере достигнуты цели обучения. Так как контроль носит в школе обучающий характер, его методы рассматриваются в тесной связи с другими методами обучения. Постоянная проверка приучает учащихся систематически работать, отчитываться перед классом за качество приобретенных знаний и умений. У учащихся вырабатывается чувство ответственности, стремление добиться лучших результатов. Контроль воспитывает целеустремленность, настойчивость и трудолюбие, умение преодолевать трудности, т.е. способствует формированию нравственных качеств личности. Систематический контроль способствует развитию самостоятельности, формированию навыков самоконтроля. Главное требование к контролю - его систематичность. Контроль результатов обучения важен и для учителя, так как позволяет ему изучать своих учащихся и корректировать учебный процесс, и для родителей, которые стремятся знать обуспехах своих детей. Контроль помогает управлять учебным процессом.
Формы и методы контроля на уроках математики
Предварительный (диагностический, стартовый) контроль предназначен для того, чтобы выявить исходный уровень знаний, от которого можно отталкиваться в последующем обучении. Он может проводиться в начале учебного года или в начале урока.
Текущий контроль осуществляется на протяжении всего урока с целью контроля усвоения изучаемого материала.
Тематический (периодический) контроль проводится в конце темы (или какого-либо длительного отрезка учебного времени - четверти, полугодия и т. п.).
Итоговый контроль проводится в конце года или в конце всего курса обучения в виде экзамена.
Контроль проводиться в форме контрольных работ, тестов, самостоятельных и проверочных работ, устного опроса, зачетов, математических диктантов, экзамен, самоконтроль и взаимоконтроль.
В результате обучения в 6 классе ученики должны
Знать:
Правила вычислений с натуральными, обыкновенными и десятичными дробями;
Определение уравнения;
Основное свойство дроби;
Свойства арифметических действий;
Формулы периметра прямоугольника, объема прямоугольного параллелепипеда, пути, стоимости, работы;
Единицы измерения длины, массы, времени, площади, объема, скорости;
Уметь:
Выполнять устно арифметические действия: сложения и вычитания двузначных чисел и десятичных дробей с двумя знаками, умножение однозначных чисел, арифметические операции с обыкновенными дробями с однозначным знаменателем и числителем;
Переходить от одной записи чисел к другой, представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной;
Записывать многозначные натуральные числа в виде разложения по степеням числа 10;
Находить значение числовых выражений;
Округлять целые числа и десятичные дроби;
Находить приближения чисел с недостатком и избытком;
Выполнять оценку значений числовых выражений;
Находить среднее арифметическое нескольких чисел;
Изображать натуральные числа, обыкновенные дроби на координатном луче; определять координаты точек на координатном луче, строить точки с заданными координатами;
Решать линейные уравнения с помощью зависимостей меду компонентами действий;
Пользоваться основными единицами длины, массы, времени, скорости, площади, объема; выражать единицы через мелкие и наоборот;
Решать текстовые задачи арифметическим способом и с помощью простейших уравнений;
Решать текстовые задачи на части и проценты;
Составлять буквенные выражения и формулы по условиям задач;
Осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, выражать из формул одну величину через остальные;
Строить и измерять отрезки с помощью линейки, углы с помощью транспортира;
Строить параллельные и перпендикулярные прямые с помощью линейки и угольника, окружности с помощью циркуля.
Общие учебные умения и навыки, и способы деятельности
В процессе освоения содержания курса математики 5-6 классов учащиеся должны развивать следующие общие учебные умения, навыки способы деятельности:
использование для познания окружающего мира методов: наблюдение, измерение, опыт, моделирование и т.д.; умение разделять процессы на этапы, звенья; выделять причинно-следственные связи;
определение адекватных способов решения учебной задачи на основе заданных алгоритмов;
сравнение, сопоставление классификация объектов;
исследование несложных практических ситуаций, выдвижение предположений, понимание необходимости их проверки на практике;
творческое решение учебных и практических задач;
адекватное восприятие устной речи и способность передавать содержание прослушанного текста в соответствии с целью учебного задания;
осознанное беглое чтение текстов;
владение монологической и диалогической речью; приведение примеров, подбор аргументов, формулирование выводов; отражение в устной и письменной речи результатов своей деятельности;
использование таблиц, схем;
использование для решения познавательных задач различных источников информации ( энциклопедии, электронные ресурсы, Интернет-ресурсы);
Самостоятельная организация учебной деятельности; владение навыками контроля и оценки своей деятельности; умение предвидеть возможные последствия своих действий. Поиск и устранение причин возникших трудностей;
Оценивание своих учебных достижений, поведения, черт своей личности, своего физического и эмоционального состояния. Соблюдение норм поведения в окружающей среде, правил здорового образа жизни;
Владение умениями совместной деятельности: согласование деятельности с другими участниками, объективное оценивание своего вклада в решение общих задач коллектива.
Оценивание своей деятельности с точки зрения нравственных ценностей.
Критерии и нормы оценивания по математике в 6 классе:
Проверка знаний, умений и навыков учащихся осуществляется посредством устных и письменных форм, интерактивных компьютерных тестов и заданий компьютерного практикума.
Устные формы контроля: беседы вопрос - ответ, устные вычислительные навыки, чтение наизусть правил, формулировок формул, алгоритмов решения различных заданий, решения заданий у доски с последующим комментарием и другое.
Письменные формы: тесты на проверку понимания и запоминания материала, контрольные работы промежуточной и тематической проверки ЗУН, самостоятельные работы, дифференцированные задания, индивидуальные карточки, домашние задания.
Система оценивания устных и письменных работ по математике
Оценка устных ответов учащихся
Вся устная работа построена таким образом, что проводится в форме теоретических зачетов, которые оцениваются следующим образом:
Ответ оценивается отметкой «5», если ученик полностью раскрыл содержание материала в объеме, предусмотренном программой, изложил материал грамотным языком, точно используя математические термины и символику в определенной последовательности, правильно выполнил рисунки и чертежи, графики, соответствующие ответу. Показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания, отвечал самостоятельно без наводящих вопросов. Возможны одна-две неточности, допущенные при освещении второстепенных вопросов или в высказываниях, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если он удовлетворяет в основном требованиям на оценку «5», но при этом имеет место один из недостатков: в изложении допущены небольшие пробелы, не исказившие математического содержания ответа; допущены одна-две неточности при освещении основного содержания ответа, исправленные после замечания учителя; допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в высказываниях, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «3» в следующих случаях: неполно раскрыто содержание материала; имелись затруднения или допущены ошибки в определении понятий, использовании математической терминологии, чертежах, выкладках, исправленных после нескольких наводящих вопросов учителя; ученик не справился с применением теории в новой ситуации при выполнении задания, но выполнил задания базового уровня по данной теме; при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Ответ оценивается отметкой «2» в следующем случае: не раскрыто основное содержание учебного материала, допущены ошибки в определении понятий, при использовании математической терминологии; обнаружено незнание или непонимание большей или наиболее важной части учебного материала. Выяснено полное незнание и непонимание изучаемого учебного материала; ученик не смог ответить ни на один из поставленных вопросов по изучаемому материалу или отказался отвечать.
Зачет может быть пересдан в течении двух дней, если ребенок пропустил его по уважительной причине или хочет повысить качество знаний по изучаемой теме.
Работа на уроках математики построена в форме индивидуального контроля выполнения задания каждым учеником на всех этапах решения задачи, эта работа не оценивается, она носит обучающий коррекционный смысл.
Оценка письменных ответов учащихся
Письменный опрос проводиться в нескольких формах: практическая работа, проверочная или самостоятельная работа контролирующего характера, контрольная работа в традиционной форме, контрольная работа в форме тестирования, практические зачеты.
Все они оцениваются в следующей форме:
Отметка «5» выставляется, если выполнены без ошибок все задания, работа может содержать не более двух недочетов.
Отметка «4» выставляется, если а) выполнены без ошибок все задания, но работа может содержать более двух недочетов; б) не решено одно из заданий повышенного уровня, а все остальные задания выполнены без ошибок.
Отметка «3» выставляется, если выполнены без ошибок все задания базового уровня (первой части).
Отметка «2» выставляется, если выполнены не все задания базового уровня, или не приступал к работе.
К ошибкам относятся погрешности, которые обнаруживают незнание учащимися формул, правил, основных свойств и неумение их применять, потеря корня или сохранение посторонних корней в ответе, неумение строить и читать графики функций в объеме программных требований, а также вычислительные ошибки, если они не являются опиской.
К недочетам относятся описки, недостаточность или отсутствие необходимых пояснений в решении текстовых задач.
Если одна и та же ошибка (один и тот же недочет) встречается несколько раз, то это рассматривается как одна ошибка (один недочет). Встречающиеся в работе зачеркивания, свидетельствующие о поисках решения, считать погрешностью не следует. Исправления корректором считаются недочетами.
Контрольные работы в тестовой форме оцениваются по разработанным шкалам.
Все оценки выставляются в журнал. За выполнение обучающих самостоятельных работ выставляются оценки только по желанию учащихся (положительные оценки).
Зачет – это специальный вид контроля, целью которого является проверка достижения учащимися уровня обязательной подготовки.
Содержание зачетных работ отбирается таким образом, чтобы обязательные результаты обучения были представлены максимально полно.
Каждый ученик сдает все предусмотренные планом зачеты.
Достижение учеником уровня обязательной подготовки оценивается по двухбалльной системе «зачтено» (в журнал выставляется оценка 4 или 5) или «не зачтено».
Зачет считается сданным, если ученик выполнил верно, все предложенные ему задачи. Если допущены недочеты, то зачет считается выполненным, но выставляется отметка «4». В противном случае оценка «зачтено» не выставляется. При этом зачет подлежит пересдаче. Ученик пересдает не весь зачет целиком, а только те виды задач, с которыми он не справился.
Итоговое оценивание знаний школьника (за четверть, полугодие, год) непосредственно зависит от результатов контрольный контрольных работ. Оценка является положительной только при условии, если все зачеты за этот период учеником сданы и выполнены все контрольные работы. Таким образом, для выставления четвертной и полугодовой отметки, учащиеся должны пересдавать все пропущенные зачеты и к/р. В случае отсутствия ученика на занятиях по уважительной причине более двух недель оценка за четверть может быть выставлена на основании текущих оценок.
Обязательные результаты обучения
Математика – 6
Умение решать задачи, аналогичные данным, обеспечивает выполнение программных требований, и необходимо для дальнейшего изучения курса математики и смежных дисциплин. Ниже приведенные задачи характеризуют уровень, достижение которого достаточно для выставления положительной оценки.
Числа и вычисления
В результате изучения курса математики учащиеся должны:
Правильно употреблять термины, связанные с различными видами чисел и способами их записи: целое, дробное, рациональное, иррациональное, положительное, десятичная дробь и др. (например, переходить от одной формы записи чисел к другой; пре6дставлять десятичную дробь в виде обыкновенной, проценты – в виде десятичной дроби и т. п.).









![]()
![]()

 Какая часть круга закрашена (рис. 1) Выразите ответ: а) обыкновенной дробью; б) десятичной дробью; в) в процентах.
Какая часть круга закрашена (рис. 1) Выразите ответ: а) обыкновенной дробью; б) десятичной дробью; в) в процентах.
Рис. 1
Представьте: а) число 0,35 в виде обыкновенной дроби; б) число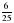 в виде десятичной дроби.
в виде десятичной дроби.
Выразите в процентах десятичные дроби: 0,17; 0,02; 0,2.
Представьте в виде десятичной дроби: 23%, 7%.
Сколько примерно процентов составляет 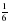 населения города?
населения города?
Сравнивать числа, упорядочивать наборы чисел; понимать связь отношений «больше» и «меньше» с положением точек на координатной прямой.
Сравните числа:
1,259 и 1,27.
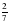 и
и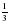 ;
; 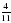 и 0,36; -
и 0,36; - 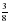 и –0,4.
и –0,4.
Расположите числа 6; -11; -3 в порядке возрастания.
Укажите числа, соответствующие точкам А, В и С координатной прямой (рис. 2).
![]()
![]()
![]()
![]()
![]() А В С
А В С
![]()
 ● ●
● ●
х
-1 0 1 2 3
Рис. 2
Выполнять арифметические действия с рациональными числами, находить значения степеней и квадратных корней; сочетать при вычислениях устные и письменные приемы, применение калькулятора.
Вычислите:
2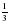 +
+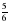 ;
; 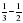 ;
; 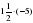 ;
; 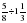 ; –1,3 - 2,8.
; –1,3 - 2,8.
(-0,4)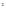 ; (
; (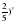 .
.
Найдите значения выражения:
21,15 14,1 - 2,8 0,125.
2,63 - 0,8 (2,4 + 0,45).
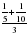 .
.
–1,5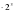 +3.
+3.
8 – 12 + 11 – 9.
Составлять и решать пропорции, решать основные задачи на дроби, проценты.
Найдите неизвестный член пропорции 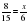 .
.
Чтобы сшить 6 юбок, требуется 9 м ткани. Сколько таких юбок получится из 15 м такой ткани
Трое рабочих выполнят работу за 8 дней. Сколько нужно рабочих, чтобы выполнить ту же работу за 4 дня
В зрительном зале 120 мест. Во время спектакля занято 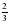 всех мест. Сколько свободных мест в зрительном зале
всех мест. Сколько свободных мест в зрительном зале
цена товара 760 р. определите новую цену товара при снижении цен на 5%.
Округлять целые числа и десятичные дроби, понимать смысл записи, а = 7,3 0,14, производить прикидку и оценку результата вычислений.
На футбольный матч было продано 29 362 билета. Укажите примерное количество зрителей на матче, округлив это число: а) до сотен; б) до тысяч; в) до десятков тысяч.
В системе русских мер веса (ХVIII в.) 1 золотник примерно равен 4,266 г. Укажите приближенное значение этой меры, округлив данное: а) до единиц; б) до десятых; в) до сотых.
Выражения и их преобразования
В результате изучения курса математики учащиеся должны:
правильно употреблять термины «выражение», «тождественное преобразование», понимать их в тексте, в речи учителя, понимать формулировку заданий: «упростить выражение»;
составлять несложные буквенные выражения и формулы; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления.
Найти значение выражения:
4а2-3а при а = 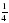 .
.
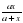 при а =
при а = 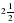 , х =
, х = 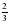 .
.
-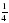 ху при х = 2, у = 6.
ху при х = 2, у = 6.
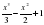 при х = -1.
при х = -1.
а - 2b + с при а =1,3; b = -0,6; с = -3,5.
Уравнения и неравенства
В результате изучения курса математики учащиеся должны:
понимать, что уравнения – это математический аппарат решения разнообразных задач из математики, смежных областей знаний, практики;
решать линейные уравнения.
Решить уравнение:
36. 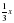 = -2.
= -2.
4 - 5(3х+2,5) = 3х + 0,5.
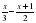 = 0
= 0
Решать текстовые задачи с помощью составления уравнений.
Решить задачу:
Периметр треугольника АВС равен 28 м. Сторона АВ на 1 м больше стороны ВС, а сторона Ас в 2 раза больше стороны ВС. Найдите стороны треугольника АВС.
Катер проходит расстояние между пристанями по течению реки за 2 ч, а против течения – за 3 ч. Скорость течения реки – 2 км/ч. найдите скорость катера в стоячей воде и расстояние между пристанями.
Диагностическая контрольная работа
по математике 6 класс (40 мин)
Цель: проверка и оценка остаточных знаний за курс математики 5 класса.
Вариант I
Вычислите сумму и разность:
а) 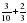 ; б) 2
; б) 2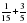 ; в)
; в) 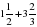 ; г)
; г) 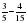 ; д) 1-
; д) 1- 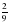 ; е)5 - 1
; е)5 - 1 ; ж)1
; ж)1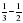 ; з) 3
; з) 3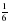 - 1
- 1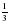 .
.
Вычислите произведение и частное:
а)  •
•  ; б)
; б)  • 40; в) 24 •
• 40; в) 24 • 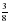 ; г) 1
; г) 1 • 2
• 2 ; д)
; д) :
:  ; е)
; е)  : 60; ж) 1
: 60; ж) 1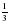 :
: 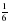 ; з) 50 : 8.
; з) 50 : 8.
Найдите  от 140 км.
от 140 км.
От куска ткани отрезали 10 м, что составляет  ее длины. Сколько метров ткани было в куске?
ее длины. Сколько метров ткани было в куске?
Построить угол, равный 46º, определить вид угла.
Вариант II
Вычислите сумму и разность:
а)  ; б) 3
; б) 3 ; в) 2
; в) 2  + 1
+ 1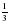 ; г)
; г)  -
-  ; д) 1 -
; д) 1 -  ; е) 7 - 2
; е) 7 - 2 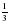 ; ж) 1
; ж) 1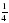 -
- 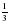 ; з) 2
; з) 2 - 1
- 1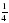 .
.
Вычислите произведение и частное:
а) •
•  ; б) 36 •
; б) 36 •  ; в)
; в) 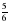 • 30; г) 4
• 30; г) 4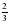 •
•  ; д)
; д)  :
:  ; е) 7 :
; е) 7 :  ; ж) 1
; ж) 1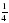 :
: ; г)30 : 9.
; г)30 : 9.
Найдите  от 100 км.
от 100 км.
Из пакета отсыпали 15 г перца, что составляет  содержимого пакета. Сколько граммов перца было в пакете?
содержимого пакета. Сколько граммов перца было в пакете?
Построить угол, равный 123º, определить вид угла.
Система оценивания.
Оценка «3» ставится за верно выполненные задания 1,2 и 3.
Оценка «4» ставится за верно выполненные задания 1,2,3,4 или выполнены все задания, но допущены более двух недочетов.
Оценка «5» ставится за верное выполнение всех заданий, допускается не более двух недочетов.
Измеритель
достижений учащимися уровня знаний и умений
Предмет: математика
Класс: 6 класс
Время проведения: 2 неделя сентября
Время на уроке: 40 минут.
Форма измерителя: контрольная работа, содержащая задания со свободным ответом.
Тема: «Диагностическая работа».
Цель контроля: проверка и оценка остаточных знаний за курс математики 5 класса.
Образовательный стандарт: базовый.
Количество вариантов: 2
Перечень структурных элементов, подлежащих контролю:
| № | Содержание задания |
| 1 | Сложение обыкновенных дробей, сложение смешанного числа с обыкновенной дробью, сложение смешанных чисел, вычитание обыкновенных дробей, вычитание обыкновенной дроби из единицы, вычитание смешанного числа из целого, вычитание обыкновенной дроби из смешанного числа, вычитание смешанных чисел. |
| 2 | Умножение обыкновенных дробей, умножение целого числа на обыкновенную дробь, умножение обыкновенной дроби на целое число, деление обыкновенных дробей, деление обыкновенной дроби на целое число, деление смешанного числа на обыкновенную дробь, деление целого числа на целое. |
| 3 | Нахождение дроби от числа, умножение целого числа на дробь. |
| 4 | Нахождение числа по его дроби, деление целого числа на дробь. |
| 5 | Построение угла по заданной градусной мере, вид угла. |
Критерии оценивания
за 2 задание ученик может получить 8 баллов (по 1 баллу за каждый структурный элемент);
за 3 задание ученик может получить 2 балла (по 1 баллу за каждый структурный элемент);
за 4 задание ученик может получить 2 балла (по 1 баллу за каждый структурный элемент))
За 5 задание ученик может получить 2 балла (по 1 баллу за каждый структурный элемент).
Оценочные нормы
оценка «5» ставится за 21 – 22 баллов;
оценка «4» ставится за 19 – 20 баллов;
оценка «3» ставится за 16 – 18 баллов;
оценка «2» ставится за 0 – 15 баллов.
Ключ
1 задание:  .
.
2 задание:  .
.
3 задание: 60 км.
4 задание: 16 м.
5 задание: острый угол.
Итоговая контрольная работа №11
за курс 6 класса (40 мин)
Вариант I
Найдите значение выражения: 36 : 1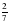 - 19,8 + 2
- 19,8 + 2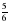
Решите уравнение: 1,2 x – 0,6 = 0,8 x – 27
Постройте отрезок АК, где А ( 2; 5 ) и К ( - 4; - 1 ) и запишите координаты точек пересечения этого отрезка с осями координат.
Решите с помощью уравнения задачу: « За два дня на элеватор отправили 574 m зерна, причем в I день в 1,8 раза меньше, чем во II день. Сколько тонн зерна было отправлено в I день и сколько во II
На экзамене 30% шестиклассников получили оценку « 5 » . Сколько учеников в классе, если пятерки получили 9 человек?
Вариант II
Найдите значение выражения: 42 : 1 - 15,6 + 1
- 15,6 + 1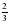
Решите уравнение: 1,4 x + 14 = 0,6 x + 0,4
Постройте отрезок ВМ, где В ( - 1 ; 4 ) и М ( 5 ; - 2 ) и запишите координаты точек пересечения этого отрезка с осями координат.
Решите с помощью уравнения задачу: « В школе 671 ученик, причем девочек в 1,2 раза больше, чем мальчиков. Сколько девочек и сколько мальчиков учатся в школе?
Тракторист вспахал 70% поля. Какова площадь поля, если вспахано 56 га?
Система оценивания.
Оценка «3» ставится за верно выполненные задания 1,2 и 3.
Оценка «4» ставится за верно выполненные задания 1,2,3,4 или выполнены все задания, но допущены более двух недочетов.
Оценка «5» ставится за верное выполнение всех заданий, допускается не более двух недочетов.
Измеритель
достижений учащимися уровня знаний и умений
Предмет: математика
Класс: 6 класс
Время проведения: 3 неделя мая
Время на уроке: 40 минут.
Форма измерителя: контрольная работа, содержащая задания со свободным ответом.
Тема: «Итоговая работа».
Цель контроля: итоговый контроль умений и навыков за курс математики 6 класса.
Образовательный стандарт: базовый.
Количество вариантов: 2
Перечень структурных элементов, подлежащих контролю:
| № | Содержание задания |
| 1 | Деление натурального числа на смешанное число, вычитание из целого числа десятичной дроби, сложение десятичной дроби и смешанного числа, ответ |
| 2 | Перенос членов из одной части уравнения в другую, приведение подобных членов, деление числа, стоящего в правой части уравнения, на число, стоящее перед неизвестной (коэффициент), ответ. |
| 3 | Построение прямоугольной системы координат, построение точек по заданным координатам, нахождение координат точек пересечения отрезка с осями координат. |
|
4 | Введение неизвестной величины, выражение через нее других неизвестных величин, составление уравнения по условию задачи, решение уравнения по алгоритму, нахождение всех неизвестных величин, ответ. |
| 5 | Нахождение числа по его проценту, ответ |
Критерии оценивания
за 2 задание ученик может получить 4 балла (по 1 баллу за каждый структурный элемент);
за 3 задание ученик может получить 3 балла (по 1 баллу за каждый структурный элемент);
за 4 задание ученик может получить 6 баллов (по 1 баллу за каждый структурный элемент))
За 5 задание ученик может получить 2 балла (по 1 баллу за каждый структурный элемент).
Оценочные нормы
оценка «5» ставится за 18 – 19 баллов;
оценка «4» ставится за 15 – 17 баллов;
оценка «3» ставится за 11 – 14 баллов;
оценка «2» ставится за 0 – 10 баллов.
Ключ









 Какая часть круга закрашена (рис. 1) Выразите ответ: а) обыкновенной дробью; б) десятичной дробью; в) в процентах.
Какая часть круга закрашена (рис. 1) Выразите ответ: а) обыкновенной дробью; б) десятичной дробью; в) в процентах.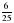 в виде десятичной дроби.
в виде десятичной дроби.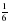 населения города?
населения города?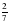 и
и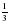
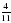 и 0,36
и 0,36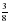 и –0,4.
и –0,4. ● ●
● ●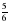 ;
; 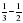 ;
; 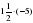 ;
; 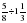 ; –1,3 - 2,8.
; –1,3 - 2,8. ; (
; (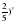 .
.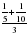 .
.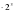 +3.
+3.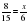 .
.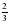 всех мест. Сколько свободных мест в зрительном зале
всех мест. Сколько свободных мест в зрительном зале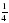 .
.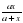 при а =
при а = 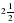 , х =
, х = 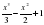 при х = -1.
при х = -1.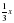 = -2.
= -2.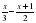 = 0
= 0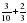 ; б) 2
; б) 2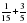 ; в)
; в) 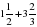 ; г)
; г) 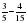 ; д) 1-
; д) 1- 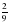 ; е)5 - 1
; е)5 - 1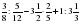
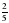 стакана. Сколько граммов крупы насыпали в стакан?
стакана. Сколько граммов крупы насыпали в стакан?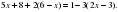
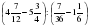
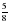 этой площади. Определите площадь окон, вымытых за час.
этой площади. Определите площадь окон, вымытых за час.