| Рассмотрено Руководитель МО _________/Минегулова В.М./ Протокол № 1 от «20» августа 2016 г. | Согласовано Заместитель директора по УР МБОУ «СОШ № __» НМР РТ _______ /Мухамедъярова Г.Х./ от «26» августа 2016 г. | Утверждаю Директор МБОУ «СОШ № _» НМР РТ ______________/Фахрутдинова Н.М. / Приказ № 386 от « 1 » сентября 2016г. |
РАБОЧАЯ ПРОГРАММА
по математике для 8 А, Б,В класса
Минегуловой Венеры Магсумовны
учителя без квалификационной категории
МБОУ «СОШ №6» НМР РТ
г. Нижнекамск, 2016 год
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Рабочая программа по предмету «Математика» в 8-ом классе ориентирована на учащихся 8 класса А,Б,В и составлена на основе следующих документов:
1.Федеральный компонент государственного образовательного стандарта основного общего образования (утвержденного приказом МО и Н РФ №1089 от 5 марта 2004 года; Приказ Министерства образования и науки РФ от 23 июня 2015 г. N 609«О внесении изменений в федеральный компонент государственных образовательных стандартов начального общего, основного общего и среднего (полного) общего образования.
2.Примерная программа основного общего образования по математике.
3.Основная образовательная программа основного общего образования МБОУ «СОШ №6»НМР РТ
4.Учебный план МБОУ «СОШ №6» НМР РТ на 2016-2017 учебный год
5. Положение о рабочей программе учителя МБОУ «СОШ №6»НМР РТ в соответствии с ФК ГОС
Согласно федеральному базисному учебному плану для образовательных учреждений Российской Федерации на изучение математики на ступени основного общего образования отводится 5 ч , что составляет 175 часов в учебный год.
Уровень обучения – базовый.
Примерная программа 7 конкретизирует содержание предметных тем образовательного стандарта и даёт примерное распределение учебных часов по разделам курса.
Цель и задачи изучения:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса;
приобретение конкретных знаний о пространстве и практически значимых умений, формирование языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания обучающихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.
Место предмета в учебном плане
Математическое образование в основной школе складывается из следующих содержательных компонентов (точные названия блоков): арифметика; алгебра; геометрия; элементы комбинаторики, теории вероятностей, статистики и логики. В своей совокупности они отражают богатый опыт обучения математике в нашей стране, учитывают современные тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационно емком и практически значимом материале. Эти содержательные компоненты, развиваясь на протяжении всех лет обучения, естественным образом переплетаются и взаимодействуют в учебных курсах.
Арифметика призвана способствовать приобретению практических навыков, необходимых для повседневной жизни. Она служит базой для всего дальнейшего изучения математики, способствует логическому развитию и формированию умения пользоваться алгоритмами.
Алгебра. Изучение алгебры нацелено на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира (одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у обучающихся представлений о роли математики в развитии цивилизации и культуры.
Геометрия — один из важнейших компонентов математического образования, необходимый для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания обучающихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.
Элементы логики, комбинаторики, статистики и теории вероятностей становятся обязательным компонентом школьного образования, усиливающим его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования функциональной грамотности – умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчёты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчёт числа вариантов, в том числе в простейших прикладных задачах.
При изучении статистики и теории вероятностей обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации и закладываются основы вероятностного мышления.
Таким образом, в ходе освоения содержания курса учащиеся получают возможность:
развить представление о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами;
получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
развить логическое мышление и речь – умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
Тематическое распределение количества часов и основное содержание обучения.
Повторение (8ч.)
Рациональные дроби (22ч)
Рациональная дробь. Основное свойство дроби, сокращение дробей. Тождественные преобразования рациональных выражений. Функция у = к/х и ее график.
Понятия дробного выражения, рациональной дроби. Основное свойство дроби. Правило об изменении знака перед дробью. Правила сложения, вычитания дробей с одинаковыми и с разными знаменателями. Правила умножения, деления дробей, возведения дроби в степень. Понятие тождества, тождественно равных выражений, тождественных преобразований выражения. Рациональные выражения и их преобразования. Свойства и график функции
у = 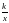 при k 0; при k 0.
при k 0; при k 0.
Четырехугольники (14 ч). Параллелограмм, его свойства и признаки. Прямоугольник, квадрат, ромб, их свойства и признаки. Трапеция, средняя линия трапеции; равнобедренная трапеция
Квадратные корни (18 ч)
Понятие об иррациональных числах. Общие сведения о действительных числах. Квадратный корень. Понятие о нахождении приближенного значения квадратного корня. Свойства квадратных корней. Преобразования выражений, содержащих квадратные корни. Функция  ее свойства и график.
ее свойства и график.
Понятие рационального, иррационального, действительно числа, определение арифметического корня, теоремы о квадратном корне из произведения, из дроби, тождество  = |x|.
= |x|.
Площадь (14 ч). Площадь прямоугольника. Площадь параллелограмма, треугольника и трапеции (основные формулы
Теорема Пифагора. Признаки равенства прямоугольных треугольников. Синус, косинус, тангенс, котангенс острого угла прямоугольного треугольника и углов от 0° до 180°; приведение к острому углу. Решение прямоугольных треугольников.
Квадратные уравнения (24 ч)
Квадратное уравнение. Формула корней квадратного уравнения. Решение рациональных уравнений. Решение задач, приводящих к квадратным уравнениям и простейшим рациональным уравнениям.
Треугольники (20 ч). Признаки подобия треугольников.
Соотношения между сторонами и углами прямоугольного треугольника (5 ч). Основное тригонометрическое тождество. Формулы, связывающие синус, косинус, тангенс, котангенс одного и того же угла. Теорема косинусов и теорема синусов; примеры их применения для вычисления элементов треугольника.
Неравенства (19 ч)
Числовые неравенства и их свойства. Почленное сложение и умножение числовых неравенств. Погрешность и точность приближения. Линейные неравенства с одной переменной и их системы.
Окружность (16 ч). Центр, радиус, диаметр. Дуга, хорда. Центральный, вписанный угол; величина вписанного угла. Взаимное расположение прямой и окружности, двух окружностей. Касательная и секущая к окружности; равенство касательных, проведенных из одной точки. Метрические соотношения в окружности: свойства секущих, касательных, хорд.
Окружность, вписанная в треугольник, и окружность, описанная около треугольника. Вписанные и описанные четырехугольники. Вписанные и описанные окружности правильного многоугольника.
Степень с целым показателем. Элементы статистики (11 ч).
Степень с целым показателем и ее свойства. Стандартный вид числа. Приближенный вычисления.
Повторение (9 ч)
Требования к подготовке учащихся по предмету к концу учебного года
В результате изучения алгебры ученик должен
знать/понимать
существо понятия математического доказательства; примеры доказательств;
существо понятия алгоритма; примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации.
выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним;
решать линейные неравенства с одной переменной и их системы;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
описывать свойства изученных функций, строить их графики; использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами;
нахождения нужной формулы в справочных материалах;
моделирования практических ситуаций и исследования построенных моделей с использованием аппарата алгебры;
описания зависимостей между физическими величинами соответствующими
В результате изучения геометрии ученик должен
Уметь объяснить, какая фигура называется многоугольником, назвать его элементы; знать, что такое периметр многоугольника, какой многоугольник называется выпуклым; уметь вывести формулу формулами при исследовании несложных практических ситуаций; суммы углов выпуклого многоугольника и решать задачи типа 364 – 370.
Уметь находить углы многоугольников, их периметры.
Знать определения параллелограмма и трапеции, виды трапеций, формулировки свойств и признаки параллелограмма и равнобедренной трапеции, уметь их
доказывать и применять при решении задач
Уметь выполнять деление отрезка на n равных частей с помощью циркуля и линейки; используя свойства параллелограмма и равнобедренной трапеции уметь доказывать некоторые утверждения.
Уметь выполнять задачи на построение четырехугольников.
Знать определения частных видов параллелограмма: прямоугольника, ромба и квадрата, формулировки их свойств и признаков.
Уметь доказывать изученные теоремы и применять их при решении задач типа 401 – 415.
Знать определения симметричных точек и фигур относительно прямой и точки.
Уметь строить симметричные точки и распознавать фигуры, обладающие осевой симметрией и центральной симметрией.
Знать основные свойства площадей и формулу для вычисления площади прямоугольника. Уметь вывести формулу для вычисления площади прямоугольника
Знать формулы для вычисления площадей параллелограмма, треугольника и трапеции; уметь их доказывать, а также знать теорему об отношении площадей треугольников, имеющих по равному углу, и уметь применять все изученные формулы при решении задач
Уметь применять все изученные формулы при решении задач, в устной форме доказывать теоремы и излагать необходимый теоретический материал.
Знать теорему Пифагора и обратную ей теорему, область применения, пифагоровы тройки. Уметь доказывать теоремы и применять их при решении задач
Знать определения пропорциональных отрезков и подобных треугольников, теорему об отношении подобных треугольников и свойство биссектрисы треугольника.
Уметь определять подобные треугольники, находить неизвестные величины из пропорциональных отношений, применять теорию при решении задач
Знать признаки подобия треугольников, определение пропорциональных отрезков. Уметь доказывать признаки подобия и применять их при решении задач
Знать теоремы о средней линии треугольника, точке пересечения медиан треугольника и пропорциональных отрезках в прямоугольном треугольнике.
Уметь доказывать эти теоремы и применять при решении задач, а также уметь с помощью циркуля и линейки делить отрезок в данном отношении и решать задачи на построение
Знать определения синуса, косинуса и тангенса острого угла прямоугольного треугольника, значения синуса, косинуса и тангенса для углов 30°, 45° и 60°, метрические соотношения. Уметь доказывать основное тригонометрическое тождество, решать задачи
Уметь применять все изученные формулы, значения синуса, косинуса, тангенса, метрические отношения при решении задач
Знать возможные случаи взаимного расположения прямой и окружности, определение касательной, свойство и признак касательной.
Уметь их доказывать и применять при решении задач, выполнять задачи на построение окружностей и касательных, определять отрезки хорд окружностей.
Знать определение центрального и вписанного углов, как определяется градусная мера дуги окружности, теорему о вписанном угле, следствия из нее и теорему о произведении отрезков пересекающихся хорд.
Уметь доказывать эти теоремы и применять при решении задач
Знать теоремы о биссектрисе угла и о серединном перпендикуляре к отрезку, их следствия, а также теорему о пересечении высот треугольника.
Уметь доказывать эти теоремы и применять их при решении задач.
Уметь выполнять построение замечательных точек треугольника.
Знать, какая окружность называется вписанной в многоугольник и какая описанной около многоугольника, теоремы об окружности, вписанной в треугольник, и об окружности, описанной около треугольника, свойства вписанного и описанного четырехугольников.
Уметь доказывать эти теоремы и применять при решении задач, выполнять задачи на построение окружностей и касательных, определять отрезки хорд окружностей.
Знать, какой угол называется центральным и какой вписанным, как определяется градусная мера дуги окружности, теорему о вписанном угле, следствия из нее и теорему о произведении отрезков пересекающихся хорд.
Уметь доказывать эти теоремы и применять при решении задач
Знать теоремы о биссектрисе угла и о серединном перпендикуляре к отрезку, их следствия, а также теорему о пересечении высот треугольника.
Уметь доказывать эти теоремы и применять их при решении задач.
Уметь выполнять построение замечательных точек треугольника.
Знать определения вектора и равных векторов.
Уметь изображать и обозначать векторы, откладывать от данной точки вектор, равный данному, решать задачи
Знать законы сложения векторов, определение разности двух векторов; знать, какой вектор называется противоположным данному; уметь объяснить, как определяется сумма двух и более векторов; уметь строить сумму двух и более данных векторов, пользуясь правилами треугольника, параллелограмма, многоугольника, строить разность двух данных векторов двумя способами.
Знать, какой вектор называется произведением вектора на число, какой отрезок называется средней линией трапеции.
Уметь формулировать свойства умножения вектора на число, формулировать и доказывать теорему о средней линии трапеции.
Литература:
Алгебра, учебник для 8 класса для общеобразовательных учреждений / Ю.Н. Макарычев, Н.Г. Миндюк, К.И.Нешков, С.Б. Суворова : Просвещение, 2011.
Геометрия, 7 – 9. Учебник для общеобразовательных учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.: Просвещение, 2013.
Алгебра: элементы статистики и теории вероятностей. Учебное пособие для учащихся 7 – 9 классов общеобразовательных учреждений / / Ю.Н. Макарычев, Н.Г. Миндюк: Просвещение.
Изучение геометрии в 7 – 9 классах. Методические рекомендации к учебнику. Книга для учителя / Л.С. Атанасян, В.Ф. Бутузов, Ю.А. Глазков: Просвещение.
Дидактические материалы по алгебре для 8 класса / В.И. Жохов, Ю.Н. Макарычев, Н.Г. Миндюк: Просвещение 2012.
Дидактические материалы по геометрии для 8 класса / Б.Г.Зив,В.М.Мейлер/ Просвещение 2010.
Календарно-тематическое планирование
| № п/п (сквозная нумерация) | Содержание (главы, темы) | Количество часов | Дата по плану | Дата по факту |
|
| Повторение | 8 |
|
|
| 1 | Повторение «Степень с натуральным показателем, ее свойства» | 1 | I.09 |
|
| 2 | Повторение «Решение линейных уравнений» | 1 | I.09 |
|
| 3 | Повторение «Решение задач с помощью уравнений» | 1 | I.09 |
|
| 4 | Повторение «Формулы сокращенного умножения» | 1 | I.09 |
|
| 5 | Повторение «Преобразование алгебраических выражений с помощью ФСУ» | 1 | I.09 |
|
| 6 | Повторение «Разложение многочлена на множители» | 1 | I.09 |
|
| 7 | Повторение «Системы линейных уравнений с двумя переменными» | 1 | I.09 |
|
| 8 | Входной контроль | 1 | II.09 |
|
|
| Рациональные дроби | 22 |
|
|
| Работа над ошибками. Понятие рационального выражения | 1 | II.09 |
|
| Нахождение ОДЗ рационального выражения | 1 | II.09 |
|
| Решение задач на тему «Рациональные выражения» | 1 | II.09 |
|
| Основное свойство дроби. Сокращение дробей
| 1 | II.09 |
|
| Решение задач на тему «Основное свойство дроби. Сокращение дробей». | 1 | III.09 |
|
| Сложение и вычитание с одинаковыми знаменателями | 1 | III.09 |
|
| Решение задач на тему «Сложение и вычитание с одинаковыми знаменателями» | 1 | III.09 |
|
| Правило сложения и вычитания дробей с разными знаменателями | 1 | III.09 |
|
| Решение задач на тему «Правило сложения и вычитания дробей с разными знаменателями» | 1 | III.09 |
|
| Сложение и вычитание дробей с разными знаменателями. | 1 | IV.09 |
|
| Обобщающий урок по теме «Сокращение, сложение и вычитание дробей» | 1 | IV.09 |
|
| Контрольная работа №1 теме «Сокращение, сложение и вычитание дробей» | 1 | IV.09 |
|
| Работа над ошибками. Умножение дробей. Возведение дроби в степень | 1 | IV.09 |
|
| Решение задач на тему «Умножение дробей. Возведение дроби в степень» | 1 | IV.09 |
|
| Деление дробей. | 1 | I.10 |
|
| Решение задач на тему «Деление дробей» | 1 | I.10 |
|
| Преобразование рациональных выражений | 1 | I.10 |
|
| Тождественные преобразования рациональных выражений | 1 | I.10 |
|
| Функция у=к/х и ее график | 1 | I.10 |
|
| Чтение графика у=к/х | 1 | II.10 |
|
| Обобщающий урок на тему « Преобразование рациональных выражений» | 1 | II.10 |
|
| 30. | Контрольная работа №2 по теме « Преобразование рациональных выражений» | 1 | II.10 |
|
|
| Четырёхугольники | 14 |
|
|
| Работа над ошибками. Выпуклые многоугольники. Сумма углов выпуклого многоугольника | 1 | II.10 |
|
| Решение задач на тему «Многоугольники» | 1 | II.10 |
|
| Параллелограмм и его свойства . | 1 | III.10 |
|
| Признаки параллелограмма | 1 | III.10 |
|
| Решение задач по теме «Параллелограмм» | 1 | III.10 |
|
| Трапеция, ее свойства. Равнобедренная трапеция, средняя линия трапеции | 1 | III.10 |
|
| Теорема Фалеса. | 1 | III.10 |
|
| Задачи на построение | 1 | IV.10 |
|
| Прямоугольник, его свойства и признаки | 1 | IV.10 |
|
| Ромб, квадрат, их свойства и признаки | 1 | IV.10 |
|
| Осевая и центральная симметрия | 1 | IV.10 |
|
| Решение задач на тему «Многоугольники» | 1 | IV.10 |
|
| Обобщающий урок на тему «Четырехугольники» | 1 | I.11 |
|
| 44. | Контрольная работа №3 по теме «Четырехугольники» | 1 | I.11 |
|
|
| Квадратные корни | 18 |
|
|
| Работа над ошибками. Рациональные числа. | 1 | I.11 |
|
| Понятие об иррациональных числах. Иррациональность числа. Десятичные приближения иррациональных чисел. | 1 | I.11 |
|
| Квадратные корни. Арифметический квадратный корень | 1 | I.11 |
|
| Решение задач на тему «Квадратные корни. Арифметический квадратный корень». | 1 | II.11 |
|
| Уравнения х² = а | 1 | II.11 |
|
| Нахождение приближенных значений квадратного корня | 1 | II.11 |
|
| Функция у=√х и её график | 1 | II.11 |
|
| Построение графика функции у=√х. использование графика для решения уравнений | 1 | II.11 |
|
| Квадратный корень из произведения и дроби | 1 | III.11 |
|
| Решение задач на тему «Квадратный корень из произведения и дроби» | 1 | III.11 |
|
| Квадратный корень из степени | 1 | III.11 |
|
| 56. | Контрольная работа №4 по теме «Определение и свойства арифметического квадратного корня» | 1 | III.11 |
|
| Работа над ошибками. Вынесение множителя из-под знака корня. | 1 | III.11 |
|
| Внесение множителя под знак корня. | 1 | IV.11 |
|
| Преобразование выражений, содержащих квадратные корни | 1 | IV.11 |
|
| Преобразование выражений, содержащих квадратные корни с использованием свойств корней | 1 | IV.11 |
|
| Преобразование выражений, содержащих квадратные корни. Разложение на множители и сокращение дробей | 1 | IV.11 |
|
| 62. | Контрольная работа №5 по теме «Квадратные корни» | 1 | IV.11 |
|
|
| Площадь | 14 |
|
|
| Работа над ошибками. Площадь многоугольника | 1 | I.12 |
|
| Площадь прямоугольника | 1 | I.12 |
|
| Площадь параллелограмма | 1 | I.12 |
|
| Решение задач на тему «Площадь параллелограмма» | 1 | I.12 |
|
| Площадь треугольника | 1 | I.12 |
|
| Площадь трапеции. | 1 | II.12 |
|
| Решение задач на тему «Площадь трапеции» | 1 | II.12 |
|
| Решение задач на тему «Площадь» | 1 | II.12 |
|
| Обобщающий урок на тему «Площадь». | 1 | II.12 |
|
| Теорема Пифагора. Теорема, обратная теореме Пифагора | 1 | II.12 |
|
| Теорема Пифагора. Теорема, обратная теореме Пифагора | 1 | III.12 |
|
| Решение задач на тему «Теорема Пифагора».
| 1 | III.12 |
|
| Обобщающий урок на тему «Теорема Пифагора» | 1 | III.12 |
|
| 76. | Контрольная работа № 6по теме «Площадь» | 1 | III.12 |
|
|
| Квадратные уравнения | 24 |
|
|
| Работа над ошибками. Определение квадратного уравнения | 1 | III.12 |
|
| Неполные квадратные уравнения. | 1 | IV.12 |
|
| Решение квадратных уравнений выделением квадрата двучлена | 1 | IV.12 |
|
| Формула корней квадратного уравнения | 1 | I.01 |
|
| Решение квадратных уравнений по формуле | 1 | I.01 |
|
| Решение квадратных уравнений различными способами | 1 | I.01 |
|
| Решение квадратных уравнений по формуле при D0 и D=0 | 1 | I.01 |
|
| Решение задач с помощью квадратных уравнений. | 1 | II.01 |
|
| Решение задач с помощью квадратных уравнений | 1 | II.01 |
|
| Теорема Виета | 1 | II.01 |
|
| Решение задач на тему «Теорема Виета» | 1 | II.01 |
|
| Обобщающий урок на тему «Квадратные уравнения» | 1 | II.01 |
|
| Контрольная работа №7 по теме «Квадратные уравнения» | 1 | III.01 |
|
| Анализ контрольной работы. Решение дробных рациональных уравнений | 1 | III.01 |
|
| Решение дробных рациональных уравнений с помощью формул корней квадр. уравнения | 1 | III.01 |
|
| Решение дробных рациональных уравнений с помощью формулы Виета | 1 | III.01 |
|
| Решение дробных рациональных уравнений с помощью формул корней квадр. уравнения и формулы Виета. | 1 | III.01 |
|
| Решение задач с помощью рациональных уравнений | 1 | IV.01 |
|
| Решение задач с помощью рациональных уравнений и с помощью формул корней квадр. уравнения | 1 | IV.01 |
|
| Решение задач с помощью рациональных уравнений с помощью формулы Виета | 1 | IV.01 |
|
| Графический способ решения уравнений | 1 | IV.01 |
|
| Уравнения с параметром | 1 | IV.01 |
|
| Обобщающий урок на тему «Дробные рациональные уравнения» | 1 | I.02 |
|
| Контрольная работа №8 по теме «Дробно-рациональные уравнения» | 1 | I.02 |
|
|
| Треугольники | 20 |
|
|
| Работа над ошибками. Определение подобных треугольников | 1 | I.02 |
|
| Отношение площадей подобных фигур | 1 | I.02 |
|
| Первый признак подобия треугольников | 1 | I.02 |
|
| Второй признак подобия треугольников | 1 | II.02 |
|
| Третий признак подобия треугольников | 1 | II.02 |
|
| Решение задач на признаки подобия треугольников | 1 | II.02 |
|
| Обобщающий урок по теме: «Признаки подобия треугольников» | 1 | II.02 |
|
| Контрольная работа №9 на тему «Признаки подобия треугольников» | 1 | II.02 |
|
| Работа над ошибками. Средняя линия треугольника | 1 | III.02 |
|
| Свойство медиан треугольника | 1 | III.02 |
|
| Пропорциональные отрезки | 1 | III.02 |
|
| Пропорциональные отрезки в прямоугольном треугольнике. | 1 | III.02 |
|
| Измерительные работы на местности | 1 | III.02 |
|
| Задачи на построение | 1 | IV.02 |
|
| Метод подобных треугольников | 1 | IV.02 |
|
| Синус, косинус и тангенс острого угла прямоугольного треугольника | 1 | IV.02 |
|
| Значения синуса, косинуса и тангенса для углов 30º, 45º, 60º, 90º | 1 | IV.02 |
|
| Соотношение между сторонами и углами прямоугольного треугольника. | 1 | IV.02 |
|
| Обобщающий урок по теме «Применение подобия треугольников. Соотношение между углами и сторонами треугольника» | 1 | II.03 |
|
| 120.
| Контрольная работа №10 по теме «Применение подобия треугольников. Соотношение между углами и сторонами треугольника» | 1 | II.03 |
|
|
| Неравенства | 19 |
|
|
| Работа над ошибками. Числовые неравенства. Определение. | 1 | II.03 |
|
| Доказательство числовых неравенств. | 1 | II.03 |
|
| Свойства числовых неравенств. Теоремы 1-3. | 1 | II.03 |
|
| Свойства числовых неравенств .Теорема 4. | 1 | III.03 |
|
| Сложение и умножение числовых неравенств. | 1 | III.03 |
|
| Погрешность и точность приближения. | 1 | III.03 |
|
| Обобщающий урок по теме «Числовые неравенства и их свойства» | 1 | III.03 |
|
|
Контрольная работа№11 по теме: «Числовые неравенства и их свойства»
| 1 | III.03 |
|
| Работа над ошибками. Пересечение и объединение множеств. | 1 | IV.03 |
|
| Числовые промежутки. | 1 | IV.03 |
|
| Решение примеров на числовые промежутки. | 1 | IV.03 |
|
| Свойства равносильности неравенств. | 1 |
|
|
| Решение неравенств с одной переменной | 1 | IV.03 |
|
| Системы неравенств с одной переменной | 1 | IV.03 |
|
| Решение систем неравенств с одной переменной | 1 | I.04 |
|
| Решение двойных неравенств | 1 | I.04 |
|
| Доказательство неравенств | 1 | I.04 |
|
| Обобщающий урок по теме «Решение неравенств одной переменной и их систем» | 1 | I.04 |
|
| 139. | Контрольная работа№12 по теме: «Неравенства с одной переменной и их системы» | 1 | I.04 |
|
|
| Окружность | 16 |
|
|
| Работа над ошибками. Взаимное расположение прямой и окружности | 1 | II.04 |
|
| Касательная к окружности | 1 | II.04 |
|
| Решение задач на тему «Касательная к окружности» | 1 | II.04 |
|
| Свойства отрезков касательных | 1 | II.04 |
|
| Центральный угол | 1 | II.04 |
|
| Теорема о вписанном угле | 1 | III.04 |
|
| Теорема об отрезках пересекающихся хорд | 1 | III.04 |
|
| Свойство биссектрисы угла | 1 | III.04 |
|
| Серединный перпендикуляр | 1 | III.04 |
|
| Теорема о точке пересечения высот треугольника. | 1 | III.04 |
|
| Вписанная окружность | 1 | IV.04 |
|
| Свойство описанного четырехугольника | 1 | IV.04 |
|
| Описанная окружность | 1 | IV.04 |
|
| Свойство вписанного четырехугольника | 1 |
|
|
| Обобщающий урок на тему «Окружность» | 1 | IV.04 |
|
| 155. | Контрольная работа №13 по теме «Окружность» | 1 | IV.04 |
|
|
| Степень с целым показателем. Элементы статистики | 11 |
|
|
| Работа над ошибками. Определение степени с целым показателем. | 1 | I.05 |
|
| Свойство степени с целым показателем. | 1 | I.05 |
|
| Применение свойств степени с целым показателем | 1 | I.05 |
|
| Решение примеров на применение свойств степени. | 1 | I.05 |
|
| Стандартный вид числа | 1 | I.05 |
|
| Представление чисел в стандартном виде. | 1 | II.05 |
|
| 162. | Контрольная работа№14 по теме: «Степень с целым показателем» | 1 | II.05 |
|
| Анализ к. р. Сбор и группировка статистических данных. | 1 | II.05 |
|
| Решение задач на сбор и группировку статистических данных | 1 |
|
|
| Наглядное представление статистической информации | 1 | II.05 |
|
| Решение задач с элементами статистики. | 1 | II.05 |
|
| Промежуточная аттестация (итоговая контрольная работа) | 1 | III.05 |
|
|
| Повторение | 9 |
|
|
| Рациональные дроби | 1 | III.05 |
|
| Квадратные корни и квадратные уравнения | 1 | III.05 |
|
| Решение задач с помощью квадратных уравнений | 1 | III.05 |
|
| Неравенства. Системы неравенств. | 1 | III.05 |
|
| Степень с целым показателем. Элементы статистики | 1 | IV.05 |
|
| Четырёхугольники. Треугольники. | 1 | IV.05 |
|
| Окружность. | 1 | IV.05 |
|
| Площадь. | 1 | IV.05 |
|





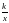 при k 0; при k 0.
при k 0; при k 0.  ее свойства и график.
ее свойства и график. = |x|.
= |x|.









