Предмет: Алгебра
Класс: 7
Количество часов: 105
Пояснительная записка
Настоящая рабочая программа разработана в соответствии с основными положениями Федерального государственного образовательного стандарта и требованиями Примерной образовательной программы основного общего образования, с учетом основных идей и положений Программы развития и формирования универсальных учебных действий и ориентирована на использование учебно-методического комплекта:
Мордкович А.Г. «Алгебра-7» часть 1, учебник – М.: Мнемозина, 2014.
Мордкович А.Г. «Алгебра-7» часть 2, задачник – М.: Мнемозина, 2014.
Александрова Л.А. «Контрольные работы. Алгебра -7» – М.: Мнемозина, 2014.
Александрова Л.А. «Самостоятельные работы. Алгебра 7» – М.: Мнемозина, 2014.
Дополнительная литература для учителя:
1. Кривоногов В.В. «Нестандартные задания по математике 5 – 11 классы», 2009.
2. Бощенко О.В. «Математика, итоговые уроки 5-9 классы», 2010.
3. Фарков А.В. «Математические олимпиады в школе 5-11 классы», 2011.
4. Максимовская М.А. и др. Тесты по математике 5-11 классы, 2011.
5. Лысенко Ф.Ф. «Тесты для промежуточной аттестации 7-8 классы», 2007.
Рабочая программа конкретизирует содержание предметных тем образовательного стандарта и показывает распределение учебных часов по разделам курса. Согласно действующему учебному плану рабочая программа предусматривает обучение в объеме 105 часов, 3 часа в неделю. С учетом уровневой специфики классов выстроена система учебных занятий (уроков), спроектированы цели, задачи, ожидаемые результаты обучения.
Общая характеристика учебного предмета
Математика играет важную роль в общей системе образования. Наряду с обеспечением высокой математической подготовки учащихся, которые в дальнейшем в своей профессиональной деятельности будут пользоваться математикой, важнейшей задачей обучения является обеспечение некоторого гарантированного уровня математической подготовки всех школьников независимо от специальности, которую они изберут в дальнейшем. Математика, давно став языком науки и техники, в настоящее время все шире проникает в повседневную жизнь и обиходный язык, внедряется в традиционно далекие от нее области.
Математическое образование является обязательной и неотъемлемой частью общего образования на всех ступенях школы. Обучение математике в основной школе направлено на достижение следующих целей:
1) в направлении личностного развития:
формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;
развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;
формирование интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;
воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;
формирование качеств мышления, необходимых для адаптации в современном информационном обществе;
развитие интереса к математическому творчеству и математических способностей;
2) в метапредметном направлении:
развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;
формирование общих способов интеллектуальной деятельности характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности;
3) в предметном направлении:
овладение математическими знаниями и умениями, необходимыми для продолжения образования, изучения смежных дисциплин, применения в повседневной жизни;
создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности.
Целью освоения дисциплины «Алгебра» в 7 классе является развитие у учащихся вычислительных умений и навыков до уровня, позволяющего уверенно использовать их при решении задач математики, смежных предметов и применять в повседневной жизни, усвоение аппарата уравнений как основного средства математического моделирования задач, осуществление функциональной подготовки школьников.
В основу изучения курса положены принципы:
дидактические (научности, сознательности и активности, наглядности, систематичности и последовательности, прочности, доступности, связи обучения с жизнью);
воспитания (социальной активности, социального творчества, развивающее воспитание, мотивированность, проблемность, индивидуализация, опора на ведущую деятельность);
развития (деятельности, непрерывности, целостного представления о мире, психологической комфортности, вариативности, творчества);
педагогики здоровья: не нанесения вреда; субъект-субъектного взаимоотношения с учащимися; соответствия содержания и организации обучения возрастным особенностям учащихся; гармоничного сочетания обучающих, воспитывающих и развивающих педагогических воздействий; приоритет активных методов обучения.
Задачи:
Обучения: овладение системой математических знаний и умений, необходимых для выполнения устных, письменных, инструментальных вычислений; овладение символическим языком алгебры, выработка формально-оперативных алгебраических умений и их применение к решению математических и нематематических задач; способствовать формированию представлений о свойствах и графиках элементарных функций и умения использовать функционально-графические представления для описания и анализа реальных зависимостей;
Развития: логического и критического мышления; математической речи; умений логически обосновывать суждения, проводить несложные систематизации; использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства; элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей; внимания, памяти.
Воспитания: качеств личности, обеспечивающих социальную мобильность: коммуникабельность, ответственность, волевые качества, способность принимать самостоятельно решения; математической культуры личности; интереса к математическому творчеству и математических способностей; отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.
Валеологические: сохранение и укрепление здоровья детей; наблюдение за посадкой детей; активное внедрение здоровьесберегающих технологий.
Срок реализации рабочей учебной программы – один учебный год.
В данном классе ведущими методами обучения предмету являются:
методы организации и осуществления учебно-познавательной деятельности: словесный (диалог, рассказ и др.); наглядный (опорные схемы, слайды и др.); практический (упражнения, практические работы, решение задач, моделирование и др.); исследовательский; самостоятельной работы; работы под руководством преподавателя; дидактическая игра;
методы стимулирования и мотивации: интереса к учению; долга и ответственности в учении;
методы контроля и самоконтроля в обучении: фронтальная устная проверка, индивидуальный устный опрос, письменный контроль (контрольные и практические работы, тестирование, письменный зачет, тесты).
На уроках используются элементы следующих педагогических технологии:
технологии на основе активизации и интенсификации деятельности учащихся (игровые технологии);
технологии на основе активизации и интенсификации деятельности учащихся (системы развивающего обучения с направленностью на развитие творческих качеств личности);
технологии на основе эффективности управления и организации учебного процесса (технология уровневой дифференциации обучения на основе обязательных результатов).
Уровень обучения: базовый.
Формы промежуточной и итоговой аттестации.
Промежуточная аттестация проводится в форме самостоятельных работ, контрольных работ, тестов, теоретических диктантов. Итоговая аттестация запланирована в виде контрольной работы.
Место дисциплины в структуре ООП ООО
Рабочая программа основного общего образования по алгебре составлена на основе Фундаментального ядра содержания общего образования и требований к результатам освоения основной общеобразовательной программы основного общего образования, представленных в Федеральном государственном образовательном стандарте общего образования. В основу содержания и структурирования данной программы, выбора приемов, методов и форм обучения положено формирование универсальных учебных действий, которые создают возможность самостоятельного успешного усвоения обучающимися новых знаний, умений и компетентностей, включая организацию усвоения, т.е. умения учиться. В процессе обучения алгебре осуществляется развитие личностных, регулятивных, познавательных и коммуникативных действий. Учащиеся продолжают овладение разнообразными способами познавательной, информационно-коммуникативной, регулятивной деятельности, приобретают и совершенствуют опыт:
| Познавательная деятельность | |
| |
| |
составлять тезисы, различные виды планов (простых, сложных и т.п.). Преобразовывать информацию из одного вида в другой (таблицу в текст, диаграмму и пр.); |
| |
понимая позицию другого человека, различать в его речи: мнение (точку зрения), доказательство (аргументы), факты; гипотезы, аксиомы, теории. Для этого самостоятельно использовать различные виды чтения (изучающее, просмотровое, ознакомительное, поисковое), приёмы слушания; |
| |
| |
| Информационно-коммуникативная деятельность | использовать мультимедийных ресурсов и компьютерных технологий для обработки, передачи, систематизации информации, создания баз данных, презентации результатов познавательной и практической деятельности; |
извлечение необходимой информации из источников, созданных в различных знаковых системах (текст, таблица, график, диаграмма, аудиовизуальный ряд и др.), отделение основной информации от второстепенной, критического оценивание достоверности полученной информации, передачи содержания информации адекватно поставленной цели (сжато, полно, выборочно); |
владения основными видами публичных выступлений (высказывание, монолог, дискуссия, полемика), следования этическим нормам и правилам ведения диалога (диспута); |
| |
| |
| |
| |
| Регулятивная деятельность | |
| |
| |
| |
работая по предложенному или самостоятельно составленному плану, использовать наряду с основными и дополнительные средства (справочная литература, сложные приборы, компьютер); |
| |
| |
| |
| |
Дисциплина «Алгебра» относится к предметной области «Математика и информатика».
Успешное освоение курса алгебры в 7 классе опирается на знания и учебные действия, формированные в курсе математики 5-6 классов.
Содержание раздела «Алгебра» способствует формированию у учащихся математического аппарата для решения задач из разных разделов математики, смежных предметов, окружающей реальности. Сознательное овладение учащимися системой математических знаний, представлений и умений необходимо для изучения физики, химии, информатики и продолжения образования. С помощью механизма логических построений вырабатывается умение формулировать, обосновывать и доказывать суждения, в том числе и нематематической природы. Освоение математики развивает и совершенствует навыки логического мышления, способствуя более успешному изучению всех школьных дисциплин. В ходе решения задач – основной учебной деятельности на уроках математики – развиваются творческая и прикладная стороны мышления.
Учебно-тематический план
| № | Раздел | Количество часов | Количество контрольных работ | Самостоятельные работы |
| 1 | Повторение курса 6 класса. | 3 | ВКР |
|
| 2 | Математический язык. Математическая модель. | 12 | 1 | 2 |
| 3 | Линейная функция | 11 | 1 | 2 |
| 4 | Система двух линейных уравнений с двумя переменными | 13 | 1 | 2 |
| 5 | Степень с натуральным показателем | 6 | 1 | 1 |
| 6 | Одночлены. Операции над одночленами | 8 | 1 | 1 |
| 7 | Многочлены. Арифметические операции над многочленами | 15 | 1 | 3 |
| 8 | Разложение многочленов на множители | 19 | 1 | 3 |
| 9 | Функция 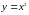 | 10 | 1 | 1 |
| 10 | Итоговое повторение | 5 | ИКР | 0 |
| 11 | Резерв | 3 | 0 | 0 |
|
| ИТОГО ЗА ГОД: | 105 | 8+2 | 15 |
Содержание учебного курса
Математический язык. Математическая модель (12 часов)
Числовые и алгебраические выражения. Переменная. Допустимое значение переменной. Недопустимое значение переменной. Первые представления о математическом языке и о математической модели. Линейные уравнения с одной переменной. Линейные уравнения как математические модели реальных ситуаций. Координатная прямая, виды промежутков на ней.
Линейная функция (11 часов)
Координатная плоскость. Алгоритм отыскания координат точки. Алгоритм построения точки М(а;b) в прямоугольной системе координат.
Линейное уравнение с двумя переменными. Решение уравнение. График уравнения. Алгоритм построения графика уравнения.
Линейная функция. Независимая переменная (аргумент). Зависимая переменная. График линейной функции. Наибольшее и наименьшее значения линейной функции на заданном промежутке. Возрастание и убывание линейной функции. Взаимное расположение графиков линейных функций.
Системы двух линейных уравнений с двумя переменными (13 часов)
Система уравнений. Решение системы уравнений. Графический способ решения уравнений. Метод подстановки. Метод алгебраического сложения.
Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций (текстовые задачи)
Степень с натуральным показателем (6 часов)
Степень. Основание степени. Показатель степени. Свойства степени с натуральным показателем. Умножение и деление степеней с одинаковыми показателями. Степень с нулевым показателем.
5. Одночлены. Операции над одночленами (8 часов)
Понятие одночлена. Коэффициент одночлена. Стандартный вид одночлена. Подобные одночлены. Арифметические операции над одночленами.
Многочлены. Арифметические операции над многочленами (15 часов)
Многочлен. Члены многочлена. Двучлен. Трехчлен. Приведение подобных слагаемых членов многочлена. Стандартный вид многочлена.
Формулы сокращенного умножения. Деление многочлена на одночлен.
Разложение многочленов на множители (19 часов)
Разложение многочлена на множители: с помощью формул сокращенного умножения, способ группировки, вынесение общего множителя за скобки, комбинированный способ. Метод выделения полного квадрата.
Понятие алгебраической дроби. Сокращение алгебраической дроби.
Тождество. Тождественно равные выражения. Тождественные преобразования.
Квадратичная функция (10 часов)
Квадратичная функция, ее свойства и график. Графическое решение уравнений. Кусочная функция. Чтение графика функции. Область определения функции. Первое представление о непрерывных функциях. Точка разрыва. Функциональная символика.
Итоговое повторение (5 часов)
Резерв (3 часа)
Учебно-методическое обеспечение
Список литературы для учителя
Основная литература:
Мордкович А.Г. «Алгебра-7» часть 1, учебник – М.: Мнемозина, 2014.
Мордкович А.Г. «Алгебра-7» часть 2, задачник – М.: Мнемозина, 2014.
Александрова Л.А. «Контрольные работы. Алгебра -7» – М.: Мнемозина, 2014.
Александрова Л.А. «Самостоятельные работы. Алгебра 7» – М.: Мнемозина, 2014.
Дополнительная литература:
1. Кривоногов В.В. «Нестандартные задания по математике 5 – 11 классы», 2009.
2. Бощенко О.В. «Математика, итоговые уроки 5-9 классы», 2010.
3. Фарков А.В. «Математические олимпиады в школе 5-11 классы», 2011.
4. Максимовская М.А. и др. Тесты по математике 5-11 классы, 2011.
5. Лысенко Ф.Ф. «Тесты для промежуточной аттестации 7-8 классы», 2007.
Список литературы для ученика
1. Мордкович А.Г. «Алгебра-7» часть 1 , учебник – М.: Мнемозина, 2014.
2. Мордкович А.Г. «Алгебра-7» часть 2, задачник – М.: Мнемозина, 2014.
3. Звавич «Дидактические материалы по алгебре, 7 класс.
Интернет ресурсы
1. http://uchitmatematika. ucos. ru
2. http://yroki. net
3. http:// rusedi.ru
4. http://www.uchportal.ru
Список литературы:
Рабочая программа по алгебре 7 класс к УМК Мордковича и др. составитель Маслакова Г.И., 2013 г.
Примерная программа основного общего образования по математике.
Требования к результатам освоения содержания курса алгебры
В результате изучения курса алгебры, обучающиеся должны:
знать:
математический язык; свойства степени с натуральным показателем; определение одночлена и многочлена, операции над одночленами и многочленами; формулы сокращенного умножения; способы разложения на множители; линейную функцию, её свойства и график; квадратичную функцию и её график; способы решения системы двух линейных уравнений с двумя переменными;
уметь: составлять математическую модель при решении задач; выполнять действия над степенями с натуральными показателями, показателем, не равным нулю, используя свойства степеней; выполнять арифметические операции над одночленами и многочленами, раскладывать многочлены на множители, используя метод вынесения общего множителя за скобки, метод группировки, формулы сокращенного умножения; строить графики линейной и квадратичной функций; решать системы двух линейных уравнений с двумя переменными; проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждений; извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики; решать комбинаторные задачи путем систематического перебора возможных вариантов, а также с использованием правила умножения.
Обладать базовыми компетенциями: использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: построения и исследования математических моделей, описания и решения прикладных задач, задач из смежных дисциплин; выполнения и самостоятельного составления алгоритмических предписаний и инструкций на математическом материале; интерпретации графиков реальных зависимостей между величинами; совершенствования навыков по использованию справочного материала и простейших вычислительных устройств.
Обладать ключевыми компетенциями:
информационно-технологическими: уметь при помощи реальных объектов и информационных технологий самостоятельно искать, отбирать, анализировать и сохранять информацию по заданной теме, интегрировать её в личный опыт; уметь представлять материал с помощью творческих работ, рефератов, средств презентации; уметь задавать и отвечать на вопросы по изучаемым темам с пониманием и по существу.
коммуникативными: уметь работать в группе: слушать и слышать других, считаться с чужим мнением и аргументировано отстаивать своё, организовывать совместную работу на основе взаимопомощи и уважения; уметь обмениваться информацией по темам; проводить доказательные рассуждения, логическое обоснование выводов, уметь различать доказанные и недоказанные утверждения; развивать у учащихся точную, экономную и информативную речь, умение отбирать наиболее подходящие языковые (в частности, символические, графические) средства.
учебно-познавательными: уметь планировать учебную деятельность: самостоятельно и мотивированно организовывать свою познавательную деятельность – ставить цель, определять задачи для её достижения; совершенствовать навыки организации учебной деятельности: организация рабочего места, режима работы; развивать навыки мыслительной деятельности: умение выделять главное, анализ и синтез, классификация, обобщение, логическое построение ответа, речи, формулирование выводов, решение задач; создать основу для осмысливания своих действий: организация само- и взаимоконтроля, рефлексивный анализ.
Обладать специальными компетенциями:
умениями и навыками построения и исследования математических моделей для описания и решения прикладных задач, задач из смежных дисциплин;
навыками выполнения и самостоятельного составления алгоритмических предписаний и инструкций на математическом материале; выполнения расчётов практического характера; использования математических формул и самостоятельного составления формул на основе обобщения частных случаев и эксперимента.
Решать следующие жизненно-практические задачи:
самостоятельно приобретать и применять знания в различных ситуациях;
работать в группах, аргументировать и отстаивать свою точку зрения, уметь слушать других;
извлекать учебную информацию на основе сопоставительного анализа объектов;
пользоваться предметным указателем, энциклопедией и справочником для нахождения информации;
самостоятельно действовать в ситуации неопределенности при решении актуальных для них проблем;
выстраивания аргументации при доказательстве;
распознавания логически некорректных рассуждений.
Критерии и нормы оценки знаний, умений и навыков обучающихся по алгебре
1. Оценка письменных контрольных работ обучающихся по алгебре.
Ответ оценивается отметкой «5», если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
Отметка «2» ставится, если:
Отметка «1» ставится, если:
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
2.
Оценка устных ответов обучающихся по алгебре. Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке обучающихся» в настоящей программе по математике);
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Отметка «1» ставится, если:
3. Общая классификация ошибок.
При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.
3.1. Грубыми считаются ошибки:
незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
незнание наименований единиц измерения;
неумение выделить в ответе главное;
неумение применять знания, алгоритмы для решения задач;
неумение делать выводы и обобщения;
неумение читать и строить графики;
неумение пользоваться первоисточниками, учебником и справочниками;
потеря корня или сохранение постороннего корня;
отбрасывание без объяснений одного из них;
равнозначные им ошибки;
вычислительные ошибки, если они не являются опиской;
логические ошибки.
3.2. К негрубым ошибкам следует отнести:
неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;
неточность графика;
нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
нерациональные методы работы со справочной и другой литературой;
неумение решать задачи, выполнять задания в общем виде.
3.3. Недочетами являются:
нерациональные приемы вычислений и преобразований;
небрежное выполнение записей, чертежей, схем, графиков.
13