Пермский муниципальный район
Муниципальное автономное общеобразовательное учреждение
«Платошинская средняя школа»
| Рассмотрено на заседании методического совета протокол № от ______________
Согласованно с заместителем директора по УВР____________ Русинова Т.П.
| УТВЕРЖДЕНО: директор______________Болгова В.Ф. приказ № от ______________________ |
Рабочая программа по алгебре для 7 класса
на 2015 - 2016 учебный год
Мелехина Галина Васильевна
учитель математики и информатики
высшей квалификационной категории
Платошино, 2015 год
Пояснительная записка
Рабочая программа составлена на основе программы «Математика 5 – 6 классы. Алгебра 7-9 классы. Алгебра и начало математического анализа 10-11 классы» для общеобразовательных школ, гимназий, лицеев по математике, рекомендованной министерством образования РФ. Составители программы: А.Г. Мордкович, И. И. Зубарева, 2009г., 2-е издание, исправленное и дополненное, изд. «Мнемозина».
Ведущим аспектом изучения курса является математическая модель – это то, что остается от реального процесса, если отвлечься от его материальной сути. Математические модели описываются математическим языком. Основная функция математического языка – организующая: таблицы, схемы, графики, алгоритмы, правила вывода, способы логически правильных рассуждений. Особая цель математического образования – развитие речи на уроках математики. В наше прагматичное время культурный человек должен уметь излагать свои мысли четко, кратко, раскладывая «по полочкам», умея за ограниченное время сформулировать главное, отсечь несущественное. Этому он учится в школе, прежде всего на уроках математики.
В центре изучения рассматриваются темы: «Математический язык. Математическая модель», «Линейная функция», «Системы двух линейных уравнений с двумя переменными», «Степень с натуральным показателем», «Одночлены. Операции над одночленами», «Многочлены. Арифметические операции над многочленами», «Разложение многочленов на множители», «Функция у=х2».
Количество часов, предусмотренное в программе, общее - 120 часов, из них: самостоятельных работ – 44 часов, контрольных работ – 8 часов.
Для подтверждения успешности обучения ученика на уроках будут использованы следующие виды работ: работа в группах, работа в парах, индивидуальная и дифференцированная работа, составление таблиц, схем, подготовка сообщений, докладов, рефератов, сравнение, анализ, работа с различными источниками информации. А так же виды уроков: урок – лекция, урок – практикум, урок – семинар, урок индивидуальной самостоятельной работы, урок самостоятельной работы в группах, урок контроля и т. д.
Основные цели и задачи математического курса в 7 классе, которые мы стремимся реализовать, заключаются в следующем: содействовать формированию культурного человека, умеющего мыслить, понимающего идеологию математического моделирования реальных процессов, владеющего математическим языком не как языком общения, а как языком организующим деятельность, умеющего самостоятельно добывать информацию и использоваться ею на практике, владеющего литературной речью и умеющего в случае необходимости простроить ее на законах математической речи.
Требования к уровню подготовки ученика 7 класса по разделам
Тема 1. Математический язык. Математическая модель
В ходе изучения алгебры в 7 классе учащиеся должны
Знать:
Понятие числового выражения;
Понятие алгебраического выражения, переменная, значение числового выражения, значение выражения с переменными;
Допустимые значения переменных;
Термины: «математический язык», «математическая модель»;
Понятие о трёх этапах математического моделирования.
Уметь:
Выполнять арифметические операции с обыкновенными дробями и десятичными дробями, с положительными и отрицательными числами;
Находить числовые значения арифметических и алгебраических выражений;
Решать линейные уравнения;
Составлять математические модели реальных ситуаций (простейший случай);
Описывать реальные ситуации, соответствующие заданной математической моделью;
Реализовывать три этапа математического моделирования в простейших ситуациях.
Тема 2. Степень с натуральным показателем и её свойства
В ходе изучения алгебры в 7 классе учащиеся должны:
Знать:
Понятия степень, основания степени, показателя степени;
Определение �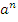 � в случае, когда n=1, и в случае, когда n – натуральное число, отличное от 1;
� в случае, когда n=1, и в случае, когда n – натуральное число, отличное от 1;
Определение степени с нулевым показателем;
Свойства степеней.
Уметь:
Вычислять �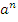 � для значений �
� для значений �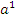 � и любых целых неотрицательных значений n;
� и любых целых неотрицательных значений n;
Пользоваться таблицей основных степеней;
Использовать свойства степени для вычисления значений арифметических и алгебраических выражений, для упрощения алгебраических выражений.
Тема 3. Одночлены. Арифметические операции над одночленами.
В ходе изучения алгебры в 7 классе учащиеся должны:
Знать:
Понятия одночлена, стандартного вида одночлена, коэффициента одночлена;
Понятия подобных одночленов;
Термины: «алгоритм», «корректные» и «некорректные» задания;
Описание словами правила арифметических операций над одночленами.
Уметь:
Приводить одночлен к стандартному виду;
Складывать и вычислять подобные одночлены, умножать одночлены, возводить одночлены в натуральную степень;
Представлять заданный одночлен в виде суммы одночленов, в виде степени одночлена;
Делить одночлен на одночлен ( в корректных случаях).
Тема 4. Многочлен. Арифметические операции над многочленами.
В ходе изучения алгебры в 7 классе учащиеся должны:
Знать:
Понятия многочлена, стандартного вида многочлена;
Уметь описать словами правила выполнения арифметических операций над многочленам и (сложение, вычитание, умножение многочлена на многочлен, умножение многочлена на одночлен);
Формулы сокращённого умножения и их словесное описание.
Уметь:
Приводить многочлен к стандартному виду;
Складывать и вычислять многочлены, приводить подобные члены, взаимно уничтожать члены многочлена;
Умножать многочлен на одночлен и на многочлен;
Применять формулы сокращённого умножения;
Делить многочлен на одночлен;
Решать уравнения, сводящиеся после выполнения арифметических операций над входящими в их состав многочленами, к уравнению вида �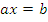 �;
�;
Решать соответствующие текстовые задачи.
Тема 5. Разложение многочлена на множители.
В ходе изучения алгебры в 7 классе учащиеся должны:
Знать:
Понятия разложения многочлена на множители, тождества, тождественно равных выражений, тождественного преобразования выражений;
Описание словами суть метода вынесения общего множителя за скобки, метода группировки;
Формулы разложения на множители, связанные с формулами сокращённого умножения.
Уметь:
Использовать для разложения многочлена на множители метод вынесения общего множителя за скобки, метод группировки, формулы сокращенного умножения, метод выделения полного квадрата;
Использование разложения для решения уравнений , для рациональных вычислений, для сокращения алгебраических дробей.
Тема 6. Линейная функция.
В ходе изучения алгебры в 7 классе учащиеся должны:
Знать:
Понятия координатной прямой, координатной плоскости, координат точек на прямой и плоскости;
Понятия линейного уравнения с двумя переменными и его решения;
Понятия линейной функции и её углового коэффициента, прямой пропорциональности;
Описание словами алгоритмов построении графиков прямой пропорциональности, линейной функции, линейного уравнений с двумя переменными;
Характеристики взаимного расположения на координатной плоскости графиков двух линейных функций, заданных аналитически.
Уметь:
Находить координаты точки в координатной плоскости, строить точки по её координатам;
Строить графики уравнений �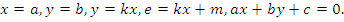 �
�
Преобразовывать линейное уравнение с двумя переменными к виду линейной функции;
Находить точки пересечения графиков двух линейных уравнений, двух линейных функций;
Находить наибольшее и наименьшее значение линейной функции на заданном числового промежутка.
Тема 7. Функция �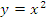 �.
�.
В ходе изучения алгебры в 7 классе учащиеся должны:
Знать:
Уметь:
Вычислять конкретные значения и построение графика функции �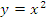 �;
�;
Строить графики функций, заданных различными формулами на различных промежутках;
Графически решать уравнение вида �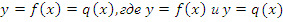 �- известные функции;
�- известные функции;
Находить наибольшие и наименьшие значения функции �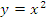 �на заданном промежутке;
�на заданном промежутке;
Читать графики;
Решать примеры на функциональную символику.
Тема 8. Системы двух линейных уравнений с двумя переменными.
В ходе изучения алгебры в 7 классе учащиеся должны:
Знать:
Понятия системы двух линейных уравнений с двумя переменными и её решения;
Описание словами графического метода решения системы, метода подстановки, метода алгебраического сложения.
Уметь:
Определять, является ли заданная пара чисел решением заданной системы уравнений или нет;
Решать системы двух линейных уравнений с двумя переменными графического сложения;
Решать задачи, сводящиеся к системам указанного вида.
Содержание программы
VII класс (I четверть — 5 ч в неделю, II, III, IV четверти — 3 ч в неделю, всего 120 ч)
1. Математический язык. Математическая модель (9 ч).
Числовые и алгебраические выражения. Первые представления о математическом языке и о математической модели. Линейные уравнения как математические модели реальных ситуаций.
Основная цель — систематизируя и обобщая сведения о преобразованиях выражений и решении линейных уравнений с одной переменной, полученные учащимися в курсе математики V—VI классов, начать знакомить учащихся с особенностями математического языка и математического моделирования.
Тема занимает ключевое положение во всем курсе алгебры VII—XI классов, во многом определяет отношение учащихся к новому учебному предмету — алгебре. Нельзя начинать изучение нового предмета, не упомянув его основную идею, на раскрытие которой фактически ориентирован весь курс. Поэтому имеет смысл планировать изучение темы так, чтобы, повторяя материал курса математики V—VI классов, постепенно вводить новые термины: математический язык, математическая модель. Школьники знакомятся с оформлением решения текстовой задачи в виде трех этапов математического моделирования: 1) составление математической модели; 2) работа с составленной моделью; 3) ответ на вопрос задачи. Эта схема используется в курсе алгебры VII—XI классов постоянно.
2. Степень с натуральным показателем и ее свойства (9 ч).
Определение степени с натуральным показателем, таблицы основных степеней, свойства степеней. Степень с нулевым показателем.
Основная цель — выработать умения выполнять действия над степенями с натуральными показателями и познакомить школьников с понятием степени с нулевым показателем.
В теме 1 курса алгебры учащимся объяснили, что математика занимается математическими моделями и что для составления математических моделей нужно владеть математическим языком. Изучение любого языка начинается с изучения простейших символов этого языка — букв. Таковыми «буквами» в математике являются числа, переменные и степени переменных. Это — основная мысль при изучении темы 2. Здесь впервые в школьном курсе алгебры появляются слова «определение», «теорема», «доказательство». Вряд ли целесообразно уже на этом этапе изучения курса требовать от всех учеников умения воспроизводить доказательства теорем. В то же время абсолютно игнорировать эти доказательства не стоит, тактика учителя должна быть гибкой, а подход к учащимся дифференцированным.
3. Одночлены. Арифметические операции над одночленами (10 ч).
Понятие одночлена, стандартный вид одночлена. Сложение и вычитание одночленов, умножение одночленов, возведение одночлена в натуральную степень. Деление одночлена на одночлен.
Основная цель — выработать умение выполнять действия над одночленами.
Основная идея этой темы практически та же, что и в теме 2, где изучались «буквы» математического языка, а здесь будут изучаться «слоги».
В основном материал темы 3 достаточно традиционен, но на два обстоятельства следует обратить внимание.
Во-первых, здесь появляется термин «алгоритм» как синоним понятия «программа действий» или «четко определенный порядок ходов». Желательно, чтобы учащиеся включили этот термин в свой рабочий словарь. При выработке алгоритмов полезно совместное творчество учителя и учащихся. Школьников следует постепенно и без нажима обучать схемам рассуждений, составлению и использованию алгоритмов и алгоритмических предписаний, поскольку этим характеризуется современный стиль обучения математике практически на всех уровнях.
Во-вторых, здесь появляются нетрадиционные для школы термины «корректная» и «некорректная» задача. Учащиеся должны знать, что далеко не всякая задача в математике решаема. Иногда она не решаема вообще, иногда она не решаема в данный момент из-за недостатка знаний у того, кто решает задачу. Наличие в процессе обучения некорректных заданий приносит несомненную пользу, так как у учащихся воспитывается способность критически анализировать ситуацию.
4. Многочлены. Арифметические операции над многочленами (20 ч).
Понятие многочлена, стандартный вид многочлена. Сложение и вычитание многочленов. Умножение многочлена на одночлен, умножение многочлена на многочлен. Формулы сокращенного умножения. Деление многочлена на одночлен. Основная цель — выработать умение выполнять действия над многочленами.
Эта тема играет фундаментальную роль в формировании умений выполнять тождественные преобразования алгебраических выражений. Изучаются алгоритмы сложения, вычитания и умножения многочленов. Важно, чтобы учащиеся поняли, что при выполнении этих действий над многочленами в результате получается многочлен, в то время как деление многочлена даже на одночлен создает проблемную ситуацию. Деление многочлена на одночлен дается в ознакомительном и опережающем плане с целью пропедевтики темы «Алгебраические дроби» и с целью показа учащимся динамики и диалектики развития математического языка. Существенную пропедевтическую роль играют вводимые здесь обозначения типа
р(х), р(х, у) — это пригодится позднее, при отработке функциональной символики.
5. Разложение многочленов на множители (22 ч).
Понятие о разложении многочлена на множители. Вынесение общего множителя за скобки. Способ группировки. Разложение многочлена на множители с помощью формул сокращенного умножения. Комбинирование различных приемов. Понятия тождества и тождественного преобразования алгебраического выражения. Первые представления об алгебраических дробях; сокращение алгебраических дробей.
Основная цель — выработать умение выполнять разложение многочленов на множители различными способами и убедить учащихся в практической пользе этих преобразований.
Первое знакомство с методом вынесения общего множителя за скобки состоялось ранее, при изучении темы «Деление многочлена на одночлен». Поэтому здесь основное внимание следует уделить выработке совместно с учащимися соответствующего алгоритма — алгоритма вынесения общего множителя за скобки.
Что касается метода группировки, то учащиеся должны понимать, что это скорее эвристический, нежели алгоритмический метод, т. е. удачную группировку нужно искать методом проб и ошибок.
Здесь впервые встречаются квадратные уравнения, решаемые методом разложения на множители. Конечно, квадратные уравнения не входят в обязательный перечень первого года изучения алгебры в школе, и учитель может все заготовки на перспективу опускать без ущерба для обучающей линии курса. Однако это обеднит эмоциональный фон курса, ослабит его развивающую линию.
Изучение многочленов в VII классе завершается темой «Сокращение алгебраических дробей». Понятие алгебраической дроби регулярно появлялось в связи с проблемой деления многочленов, и, естественно, нужно подвести какой-то итог в решении этой проблемы, причем именно в разделе о многочленах.
6. Линейная функция (15 ч).
Координатная прямая, виды промежутков на ней. Координатная плоскость. Линейное уравнение с двумя переменными и его график. Линейная функция и ее график. Отыскание наибольших и наименьших значений линейной функции на заданном промежутке. Прямая пропорциональность и ее график. Взаимное расположение графиков линейных функций.
Основная цель — познакомить учащихся с линейным уравнением с двумя переменными и линейной функцией, выработать умение строить их графики, осознать важность использования математических моделей нового вида — графических моделей.
Сначала изучается не линейная функция, а линейное уравнение с двумя переменными. Это не случайно, а напрямую связано с идейным стержнем всего курса — с математическим моделированием реальных процессов, поскольку равномерные процессы чаще всего моделируются в неявном виде — в виде уравнения ах + Ьу + с = 0, а не в явном виде — в виде линейной функции у = kx + т. Очень ответственно следует подойти к вопросу об адекватности двух моделей: линейного уравнения ах + Ьу + с = 0 и прямой в декартовой прямоугольной системе координат.
Внимание учащихся обращается на то, что график линейного уравнения с двумя переменными проще строить, если уравнение преобразовано к виду у= kx + т, для которого используется термин «линейная функция». Общее определение функции не дается, оно будет введено только в IX классе, после того как учащиеся накопят соответствующий опыт и будут в состоянии полноценно воспринять достаточно сложное математическое понятие. Вообще, не только возможно, но и полезно употребление школьниками, начиная с VII класса, таких, например, терминов, как «функция», «область определения функции», «непрерывность функции», «наибольшее и наименьшее значения функции», без знания строгих математических определений этих понятий, на описательном, наглядно-интуитивном уровне.
7. Функция у = x2 (8 ч).
Функция у = х2, ее свойства и график. Отыскание наибольших и наименьших значений функции на заданных промежутках. Графическое решение уравнений. Функции, заданные различными формулами на различных промежутках (кусочные функции). Понятие о непрерывных и разрывных функциях. Разъяснение смысла записи у = f(х). Функциональная символика.
Основная цель — показать учащимся, что, кроме линейных функций, встречаются и другие функции; сформировать навыки работы с графическими моделями.
Функция у = х2 вводится, во-первых, для того, чтобы школьник, целый год изучавший курс алгебры, не закончил этот год с убеждением, что в природе существуют только линейные функции, следует приоткрыть ему окно в дальнейшие разделы математики; во-вторых, эта функция помогает более глубокому изучению линейной функции, привлекая ее для графического решения уравнений, для построения графиков кусочных функций; в-третьих, изучение новых функций позволяет естественным образом подойти к одной из основных математических моделей всей математики — к уравнению вида y= f(х).
8. Системы двух линейных уравнений с двумя переменными (15 ч).
Основные понятия, связанные с системами двух линейных уравнений с двумя переменными. Графическое решение систем. Метод подстановки, метод алгебраического сложения. Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций (текстовые задачи).
Основная цель — научить школьников решать системы двух линейных уравнений с двумя переменными различными способами применять системы при решении текстовых задач.
9. Повторение. Решение задач (12 ч).
Шкала оценивания: критерии оценивания знаний, умений и навыков обучающихся по математике
1. Оценка письменных контрольных работ обучающихся по математике.
Ответ оценивается отметкой «5», если:
1) работа выполнена полностью;
2) в логических рассуждениях и обосновании решения нет пробелов и ошибок;
3) в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится, если:
1) работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
2)допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
1) допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
1) допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Отметка «1» ставится, если:
1)работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
2.Оценка устных ответов обучающихся по математике
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4»,
если удовлетворяет в основном требованиям на оценку «5»,
но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке учащихся» в настоящей программе по математике);
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Отметка «1» ставится, если:
Программное и учебно - методическое оснащение учебного плана
| Количество часов | Всего часов (самостоятельные/контрольные) | Реквизиты программы | УМК ученика | УМК учителя |
| I, II, III четверть – 3 часа, IV четверть – 5 часов |
120 (44/8)
| Рекомендована ДО программ и стандартов общего образования Федерального агентства по образованию А. Г. Мордкович. (Составители программы: А.Г. Мордкович, И. И. Зубарева, 2009г.)
| Мордкович А. Г. Алгебра. 7 кл.: В двух частях. Ч. 1: учебник для общеобразоват. учреждений. – 10-е изд.-м.: Мнемозина, 2007. Мордкович А. Г. Алгебра. 7 кл.: В двух частях. Ч.2: Задачник для общеобразоват. учреждений/ А. Г. Мордкович, Т. Н. мишустина, Е. Е. тульчинская.-10-е изд. – М.: мнемозина, 2008. | Алгебра. 7 класс. В 2 ч. Ч. 1. Учебник для общеобразовательных учреждений / А. Г. Мордкович. – 10-е изд., перераб. – М.: Мнемозина, 2007. Рекомендовано Министерством образования и науки РФ. Алгебра. 7 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений под редакцией А. Г. Мордкович. – 10-е изд., перераб. – М.: Мнемозина, 2007. Рекомендовано Министерством образования и науки РФ. Контрольно-измерительные материалы. Алгебра: 7 класс/Сост. Л.И. Мартышова. – М.: ВАКО, 2010. (Тесты, самостоятельные работы, контрольные работы). (ЦОР) Учебно-методический комплект. М.А. Попов. Контрольные и самостоятельные работы по алгебре. К учебнику А. Г. Мордковича «Алгебра. 7 класс» (М.: Мнемозина). 2010 г. Рекомендовано Российской Академией Образования. (ЦОР) Алгебра. 7 класс. В 2 ч. Ч. 1. Учебник для общеобразовательных учреждений / А. Г. Мордкович. Н.П. Николаев – М.: Мнемозина, 2009. Для классов с повышенным уровнем математической подготовки. Рекомендовано Министерством образования и науки РФ. (ЦОР) Алгебра. 7 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений под редакцией А. Г. Мордкович. Н.П. Николаев – М.: Мнемозина, 2009. Для классов с повышенным уровнем математической подготовки. Рекомендовано Министерством образования и науки РФ. (ЦОР) Алгебра 7 класс: методическое пособие для учителя / А.Г. Мордкович. – М.:Мнемозина, 2008. (ЦОР) Алгебра. 7 – 9 классы. Тесты для учащихся общеобразовательных учреждений / А.Г. Мордкович, Е.Е. Тульчинская. – 7-е изд., перераб. –М.:Мнемазина, 2008. (ЦОР) Алгебра. 7 класс. Дидактические материалы. Васюк Н.В., Мартиросян М.А., Слепенкова Е.В. и др. 2007г. (ЦОР) Алгебра. 7 класс. Блицопрос: пособие для учащихся общеобразовательных учреждений / Е.Е. Тульчинская. – 4-е изд., испр. И доп. – М.:Мнемозина, 2008. (ЦОР)
|
| № урока |
Тема урока | Кол- во уроков | Дата | Домашнее задание | Форма контроля | Дополнительные КИМ |
| 1 | Повторение | 1 |
|
|
|
|
| 2 | Входная контрольная работа | 1 |
|
|
|
|
| Глава 2. Математический язык. Математическая модель (15 часов) |
| 3 | Числовые и алгебраические выражения. | 4 |
| 1.6(в, г), 1.7 (в, г), 1.8 (в, г) |
| КИМ 1 КИМ 2 Блицопрос 1 |
| 4 | Числовые и алгебраические выражения. |
|
| 1.16 (в, г), 1.17(в, г), 1.42 (в), 1.43(б) |
|
| 5 | Числовые и алгебраические выражения. |
|
| 1.24(а, б), 1.25(а, б), 1.44(б) | Самостоятельная работа 1 |
| 6 | Числовые и алгебраические выражения. |
|
| §1(пример 2) 1.29(в,г), 1.30(в,г), 1.31 (в, г) | Самостоятельная работа 2 |
| 7 | Что такое математический язык. | 2 |
|
|
|
|
| 8 | Что такое математический язык. |
|
|
| Самостоятельная работа 3 | Блицопрос 2 |
| 9 | Что такое математическая модель | 3 |
|
|
|
|
| 10 | Что такое математическая модель |
|
|
|
| КИМ 3 |
| 11 | Что такое математическая модель |
|
|
| Самостоятельная работа 4 |
|
| 12 | Линейное уравнение с одной переменной | 3 |
|
|
| КИМ 4 Блицопрос 3 |
| 13 | Линейное уравнение с одной переменной |
|
|
|
|
| 14 | Линейное уравнение с одной переменной |
|
|
| Самостоятельная работа 5 |
| 15 | Координатная прямая | 2 |
|
|
| КИМ 5 Блицопрос 4 Тест1 (итоговый) |
| 16 | Координатная прямая |
|
|
| Самостоятельная работа 6 |
| 17 | Контрольная работа №1. | 1 |
|
|
|
|
| Глава 2. Линейная функция (14 часов) |
| 18 | Координатная плоскость. | 2 |
|
|
|
|
| 19 | Координатная плоскость. |
|
|
| Самостоятельная работа 7 |
|
| 20 | Линейное уравнение с двумя переменными его график. | 3 |
|
|
|
|
| 21 | Линейное уравнение с двумя переменными его график. |
|
|
|
|
|
| 22 | Линейное уравнение с двумя переменными его график. |
|
|
| Самостоятельная работа 8 | Блицопрос 5 |
| 23 | Линейная функция и её график. | 3 |
|
|
| КИМ 6 Блицопрос 6 |
| 24 | Линейная функция и её график. |
|
|
| Самостоятельная работа 9 |
| 25 | Линейная функция и её график. |
|
|
| Самостоятельная работа 10 |
| 26 | Прямая пропорциональность. | 2 |
|
|
|
|
| 27 | Прямая пропорциональность. |
|
|
| Самостоятельная работа 11 | КИМ 7 |
| 28 | Взаимное расположение графиков линейных функций. | 3 |
|
|
|
|
| 29 | Взаимное расположение графиков линейных функций. |
|
|
|
|
|
| 30 | Взаимное расположение графиков линейных функций. |
|
|
|
| Тест 2 КИМ 8 |
| 31 | Контрольная работа №2. | 1 |
|
|
|
|
| Глава 3. Системы двух линейных уравнений с двумя неизвестными (14 часов) |
| 32 | Основные понятия | 2 |
|
|
|
|
| 33 | Основные понятия |
|
|
| Самостоятельная работа 12 |
|
| 34 | Метод подстановки | 4 |
|
|
|
|
| 35 | Метод подстановки |
|
|
|
|
|
| 36 | Метод подстановки |
|
|
| Самостоятельная работа 13 |
|
| 37 | Метод подстановки |
|
|
| Самостоятельная работа 14 | Блицопрос 7 |
| 38 | Метод алгебраического сложения. | 3 |
|
|
|
|
| 39 | Метод алгебраического сложения. |
|
|
| Самостоятельная работа 15 |
|
| 40 | Метод алгебраического сложения. |
|
|
| Самостоятельная работа 16 | Блицопрос 8 |
| 41 | Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций. | 4 |
|
|
|
|
| 42 | Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций. |
|
|
|
|
|
| 43 | Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций. |
|
|
|
|
|
| 44 | Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций. |
|
|
| Самостоятельная работа 17 |
|
| 45 | Контрольная работа №3. | 1 |
|
|
|
|
| Глава 4. Степень с натуральным показателем и её свойства (8) |
| 46 | Что такое степень с натуральным показателем. | 1 |
|
| Самостоятельная работа 18 | Блицопрос 9 |
| 47 | Таблица основных степеней. | 1 |
|
| Самостоятельная работа 19 | Блицопрос 10 |
| 48 | Свойства степени с натуральным показателем | 2 |
|
|
|
|
| 49 | Свойства степени с натуральным показателем |
|
|
| Самостоятельная работа 20 | Блицопрос 11 |
| 50 | Умножение и деление степеней | 2 |
|
|
| КИМ 9 Блицопрос 12 |
| 51 | Умножение и деление степеней |
|
|
|
|
| 52 | Степень с нулевым показателем | 1 |
|
| Самостоятельная работа 21 | Тест 3 |
| 53 | Контрольная работа №4. | 1 |
|
|
|
|
| Глава 5. Одночлены. Арифметические операции над одночленами (10 часов) |
| 54 | Понятие одночлена. | 1 |
|
|
| Блицопрос 13 |
| 55 | Стандартный вид одночлена. | 1 |
|
|
|
| 56 | Сложение и вычитание одночленов. | 2 |
|
| Самостоятельная работа 22 | Тест 4 Блицопрос 14 |
| 57 | Сложение и вычитание одночленов. |
|
|
| Самостоятельная работа 23 |
| 58 | Умножение одночленов. | 2 |
|
|
|
|
| 59 | Умножение одночленов. |
|
|
| Самостоятельная работа 24 |
|
| 60 | Возведение одночлена в натуральную степень | 1 |
|
|
| Блицопрос 15 |
| 61 | Деление одночлена на одночлен. | 2 |
|
|
| КИМ 10,11 Блицопрос 16 Тест 5 |
| 62 | Деление одночлена на одночлен. |
|
|
| Самостоятельная работа 25 |
| 63 | Контрольная работа №5. | 1 |
|
|
|
|
| Глава 6. Многочлены. Арифметические операции над многочленами (19) |
| 64 | Основные понятия | 1 |
|
| Самостоятельная работа 26 | Блицопрос 17 |
| 65 | Сложение и вычитание многочленов. | 3 |
|
|
| КИМ 12 Блицопрос 18 |
| 66 | Сложение и вычитание многочленов. |
|
|
| Самостоятельная работа 27 |
| 67 | Сложение и вычитание многочленов. |
|
|
|
|
| 68 | Умножение многочлена на одночлен. | 2 |
|
| Самостоятельная работа 28 | КИМ 13 Блицопрос 19 |
| 69 | Умножение многочлена на одночлен. |
|
|
| Самостоятельная работа 29 |
| 70 | Умножение многочлена на многочлен. | 3 |
|
|
| КИМ 14 Блицопрос 20 Тест 6 |
| 71 | Умножение многочлена на многочлен. |
|
|
|
|
| 72 | Умножение многочлена на многочлен. |
|
|
| Самостоятельная работа 30 |
| 73 | Формулы сокращенного умножения. | 6 |
|
|
| . КИМ 15 Блицопрос 21, 22, 23 Тест 7 |
| 74 | Формулы сокращенного умножения. |
|
|
| Самостоятельная работа 31 |
| 75 | Формулы сокращенного умножения. |
|
|
|
|
| 76 | Формулы сокращенного умножения. |
|
|
| Самостоятельная работа 32 |
| 77 | Формулы сокращенного умножения. |
|
|
|
|
| 78 | Формулы сокращенного умножения. |
|
|
| Самостоятельная работа 33 |
| 79 | Деление многочлена на одночлен. | 3 |
|
|
|
|
| 80 | Деление многочлена на одночлен. |
|
|
|
|
|
| 81 | Деление многочлена на одночлен. |
|
|
|
| Блицопрос 24 |
| 82 | Контрольная работа №6. | 1 |
|
|
|
|
| Глава 7. Разложение многочленов на множители (21 час) |
| 83 | Что такое разложение многочленов на множители и зачем оно нужно. | 1 |
|
|
| Блицопрос 25 |
| 84 | Вынесение общего множителя за скобки. | 2 |
|
|
|
|
| 85 | Вынесение общего множителя за скобки. |
|
|
| Самостоятельная работа 34 | Блицопрос 26 |
| 86 | Способ группировки | 3 |
|
|
|
|
| 87 | Способ группировки |
|
|
| Самостоятельная работа 35 |
|
| 88 | Способ группировки |
|
|
|
| Блицопрос 27 |
| 89 | Разложение на множители с помощью формул сокращенного умножения | 6 |
|
|
| КИМ 16 Блицопрос 28 Тест 8 |
| 90 | Разложение на множители с помощью формул сокращенного умножения |
|
|
| Самостоятельная работа 36 |
| 91 | Разложение на множители с помощью формул сокращенного умножения |
|
|
|
|
| 92 | Разложение на множители с помощью формул сокращенного умножения |
|
|
| Самостоятельная работа 37 |
| 93 | Разложение на множители с помощью формул сокращенного умножения |
|
|
| Самостоятельная работа 38 |
| 94 | Разложение на множители с помощью комбинации различных приемов | 3 |
|
|
|
Блицопрос 29 Тест 9 |
| 95 | Разложение на множители с помощью комбинации различных приемов |
|
|
|
|
| 96 | Разложение на множители с помощью комбинации различных приемов |
|
|
| Самостоятельная работа 39 |
| 97 | Сокращение алгебраических дробей. | 3 |
|
|
| Блицопрос 30 |
| 98 | Сокращение алгебраических дробей. |
|
|
|
|
| 99 | Сокращение алгебраических дробей. |
|
|
| Самостоятельная работа 40 |
| 100 | Тождества. | 2 |
|
|
|
|
| 101 | Тождества. |
|
|
|
|
|
| 102 | Контрольная работа №7. | 1 |
|
|
|
|
| Глава 8. Функция 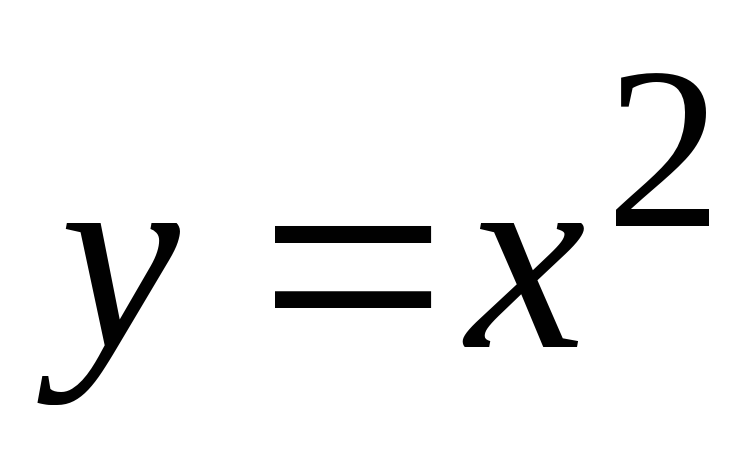 (9часов) (9часов) |
| 103 | Функция 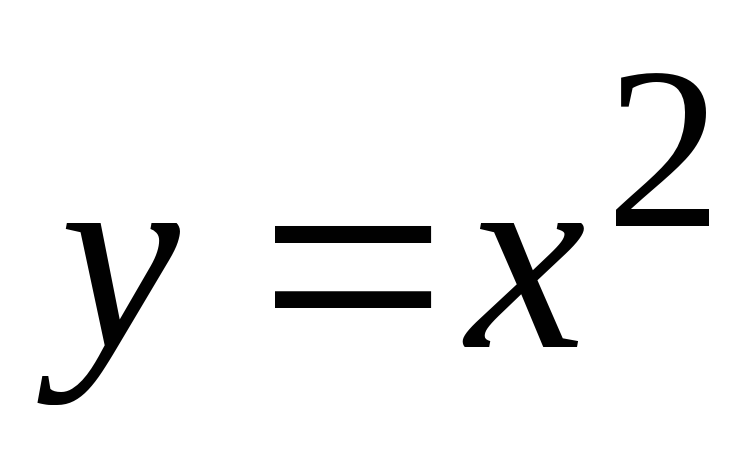 | 1 |
|
|
| Блицопрос 31 |
| 104 | График функции 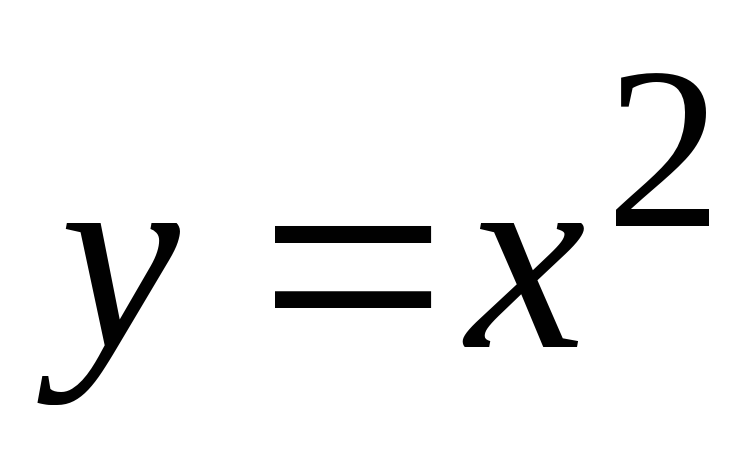 | 2 |
|
|
|
| 105 | График функции 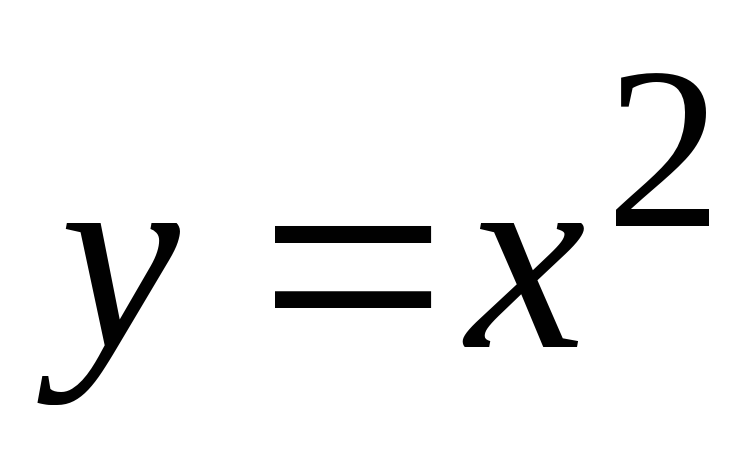 |
|
|
| Самостоятельная работа 41 |
| 106 | Графическое решение уравнений. | 2 |
|
|
|
|
| 107 | Графическое решение уравнений. |
|
|
| Самостоятельная работа 42 |
|
| 108 | Что означает запись 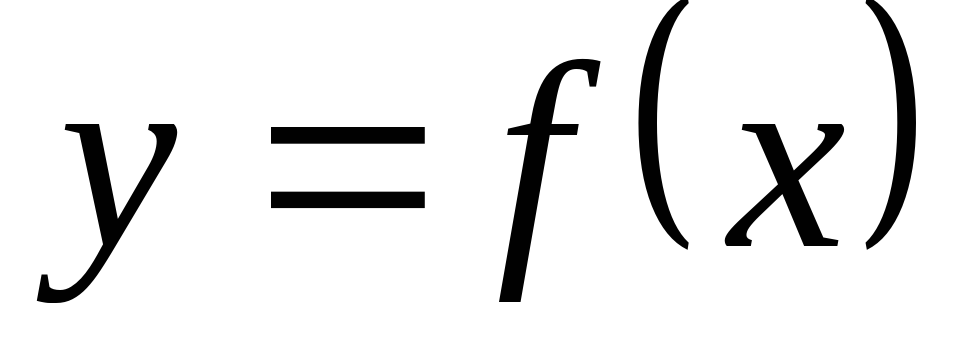 | 3 |
|
|
|
|
| 109 | Что означает запись 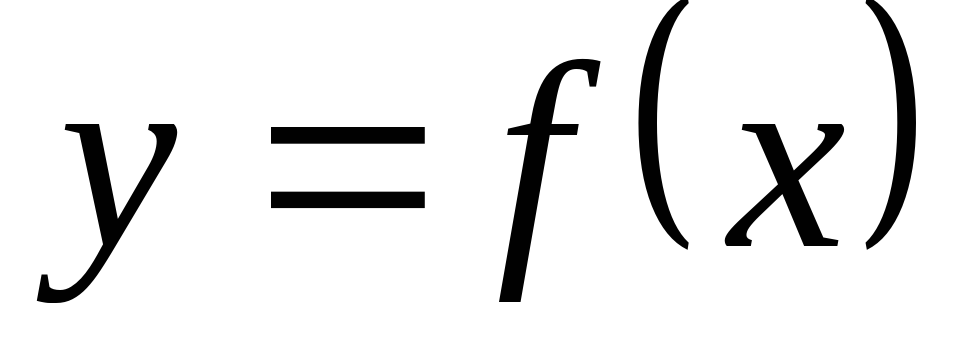 |
|
|
|
|
|
| 110 | Что означает запись 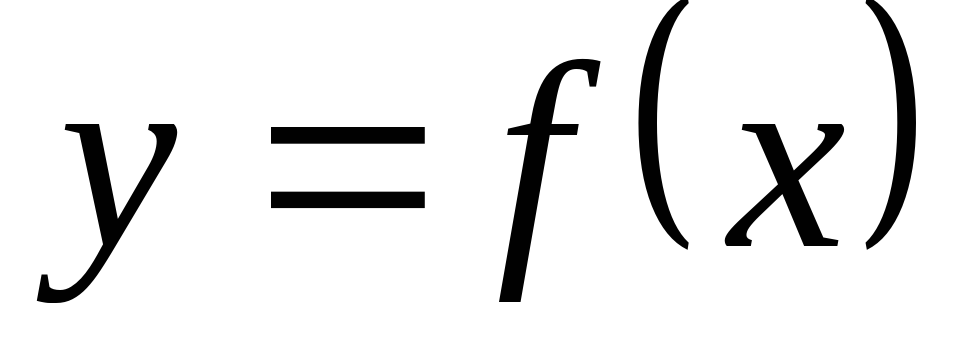 |
|
|
| Самостоятельная работа 43 | Тест 10 |
| 111 | Контрольная работа №8. | 1 |
|
|
|
|
| Простейшие комбинаторные задачи (3 часа) |
| 112 | Простейшие комбинаторные задачи |
|
|
|
|
|
| 113 | Правило умножения и дерево вариантов. |
|
|
|
|
|
| 114 | Перестановки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Повторение | 3 |
|
|
|
|
| 115 | Свойства степени с натуральным показателем Арифметические операции над многочленами |
|
|
|
|
|
| 116 | Решение уравнений |
|
|
|
|
|
| 117 | Линейная функция. Квадратичная функция. |
|
|
| Самостоятельная работа 44 |
|
| 118 | Итоговая контрольная работа |
|
|
|
|
|
| 119 | Работа над ошибками |
|
|
|
| Итоговый тест |
| 120 | Обобщающее повторение курса |
|
|
|
|
|

















