Рабочая программа по алгебре в 9 классе М.
Пояснительная записка.
Рабочая программа разработана в соответствии с основными положениями федерального государственного образовательного стандарта основного общего образования, требованиями Примерной основной образовательной программы, учебным планом МБОУ СШ № 2 г. Вязьмы Смоленской области, авторского тематического планирования учебного материала, а также планируемыми результатами основного общего образования, с учётом возможностей авторской программы «Математика» С. М. Никольского и др. и ориентирована на использование учебно-методического комплекса:
Никольский С. М. и др. Алгебра. 9 класс: учебник для общеобразовательных организаций
Потапов М. К., Шевкин А. В. Алгебра. 9 класс: дидактические материалы.
«Алгебра 9 класс» - учебник для общеобразовательных учреждений (базовый и профильный уровни), авторы С. М. Никольский, М. К. Потапов и др. – серия «МГУ - школе». Данное издание соответствует федеральным компонентам Государственного стандарта общего образования по математике и содержит материал как базового, так и профильного уровня.
Авторы учебников серии «МГУ – школе» исходят из того, что математика едина, что целей обучения математике в нескольких разных профилях можно достичь, имея один учебник, по которому курс математики может изучаться более или менее основательно в зависимости от наличия учебного времени и поставленной цели обучения. Учебники серии «МГУ – школе» устроены так, чтобы по ним можно было работать и в классе с углубленным изучением математики, и в обычном классе. При этом в одном классе могут изучаться все пункты учебника и решаться все задачи, отмеченные в учебнике как необязательные для остальных классов. За счет курсов по выбору ученик может изучить дополнительные вопросы, как из учебника, так и не включенные в учебник и отражающие специфику профиля. Дидактические материалы должны расширить задачный материал учебника и обеспечить тренинг, необходимый для поступления в вуз и обучения в нем.
В учебнике для 9 класса содержится весь материал, предусмотренный программой по математике и проектом стандарта для классов с профильным изучением математики в профильных классах, в том числе материал о корне степени n, его свойствах, степени с рациональным показателем и её свойствах, о методе математической индукции, основы тригонометрии.
Место учебного предмета в учебном плане
Базисный учебный план на изучение алгебры в 9 классе основной школы отводит 3 часа в неделю, 102 часа в год. По учебному плану МБОУ СШ № 2 г Вязьмы Смоленской области на изучение алгебры выделено 4 часа в неделю, 136 часов в год.
Общая характеристика учебного предмета
Алгебра нацелена на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира. Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов, для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры.
В ходе освоения содержания курса учащиеся получают возможность:
сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
развить логическое мышление и речь — умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
В ходе преподавания алгебры в 9 классах, работы над формированием у учащихся, перечисленных в программе знаний и умений, следует обращать внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:
решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;
исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;
проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;
поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.
Планируемые результаты освоения учебного предмета, курса
Программа обеспечивает достижение следующих результатов освоения образовательной программы основного общего образования:
личностные:
сформированность ответственного отношения к учению, готовности и способности обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию, выбору дальнейшего образования на базе ориентировки в мире профессий и профессиональных предпочтений, осознанному построению индивидуальной образовательной траектории с учетом устойчивых познавательных интересов;
сформированность целостного мировоззрения, соответствующего современному уровню развития науки и общественной практики;
сформированность коммуникативной компетентности в общении и сотрудничестве со сверстниками, старшими и младшими в образовательной, общественно полезной, учебно-исследовательской, творческой и других видов деятельности;
умения ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
представление о математической науке как сфере человеческой деятельности, об этапах ее развития, о ее значимости для развития цивилизации;
критичность мышления, умения распознавать логически некорректные высказывания, отличать гипотезу от факта;
креативность мышления, инициатива, находчивость, активность при решении алгебраических задач;
умение контролировать процесс и результат учебной математической деятельности;
способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений;
метапрпедметные:
умение самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
умение осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необходимые коррективы;
умение адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения;
осознанное вдадение логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев, установления родовидовых связей;
умение устанавливать причинно-следственные связи; строить логические рассуждения, умозаключения(индуктивные, дедуктивные и по аналогии) и выводы;
умение создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных и познавательных задач;
умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределение функции и роли участников, взаимодействие и общие способы работы; умение работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов; слушать партнера; формулировать, аргументировать и отстаивать свое мнение;
сформированность учебной и общепользовательской компетентности в область использования информационно-коммуникационных технологий (ИКТ- компетентности);
первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;
умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
умение находить в различных источниках информации, необходимую для решения математических проблем, и представлять ее в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;
умение выдвигать гипотезы при решении учебных задач и понимания необходимости их проверки;
умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;
понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;
предметные:
умение работать с математическим текстом (структурирование, извлечение необходимой информации), точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику, использовать различные языки математики ( словесный, символический, графический), обосновывать суждения, проводить классификацию, доказывать математические утверждения;
владение базовым понятийным аппаратом: иметь представление о числе, владение символьным языком алгебры, знание элементарных функциональных зависимостей, формирование представлений о статистических закономерностях в реальном мире и различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
умение выполнять арифметические преобразования рациональных выражений, применять их для решения учебных математических задач и задач, возникающих в смежных учебных предметах;
умение пользоваться изученными математическими формулами и самостоятельно составлять формулы зависимостей между величинами на основе обобщения частных случаев и эксперимента;
умение решать линейные и квадратные уравнения и неравенства, а также приводимые к ним уравнения, неравенства, системы; применять графические представления для решения и исследования уравнений, неравенств, систем; применять полученные умения для решения задач из математики, смежных предметов, практики;
овладение системой функциональных понятий, функциональным языком и символикой, умение строить графики функций, описывать их свойства, использовать функционально-графические представления для описания и анализа математических задач и реальных зависимостей
овладение основными способами представления и анализа статистических данных; умения решать задачи на нахождение частоты и вероятности случайных событий;
умение применять изученные понятия, результаты и методы при решении задач из различных разделов курса, в том числе задач, не сводящихся к непосредственному применению известных алгоритмов.
Содержание учебного предмета, курса
| № | Содержание | часы |
|
| Повторение | 3 |
-
| Неравенства. | 34 (2 к/р) |
-
| Степень числа. Функция у=хn Корень степени n | 20 (1 к/р) |
-
| Последовательности. Числовые последовательности и их свойства Арифметическая прогрессия Геометрическая прогрессия | 21 (2 к/р) |
-
| Тригонометрические формулы | 20 (2 к/р) |
-
| Элементы приближенных вычислений, статистики, комбинаторики и теории вероятностей. | 11 (1 к/р) |
-
| Повторение курса 7-9 классов. | 7(1к/р) |
-
| Всего | 136 |
Повторение (3 часа)
Линейные неравенства с одним неизвестным (9 часов)
Неравенства первой степени с одним неизвестным, применение графиков к решению неравенств первой степени с одним неизвестным, линейные неравенства с одним неизвестным, системы линейных неравенств с одним неизвестным
Основная цель – систематизировать и обобщить уже известные сведения о неравенствах первой степени, систем неравенств первой степени, сформировать представление о свойствах неравенств первой степени и умение применять их при решении.
Неравенства второй степени с одним неизвестным (9 часов, из них 1 контрольная работа)
Понятие неравенства второй степени с одним неизвестным, неравенства второй степени с положительным дискриминантом, неравенства второй степени с дискриминантом, равным нулю, неравенства второй степени с отрицательным дискриминантом, неравенства, сводящиеся к неравенствам второй степени.
Основная цель – систематизировать и обобщить сведения о неравенствах второй степени в зависимости от дискриминанта, сформировать умение решать неравенства второй степени
Рациональные неравенства (16 часов, из них 1 контрольная работа)
Метод интервалов, решение рациональных неравенств, системы рациональных неравенств, нестрогие рациональные неравенства.
Основная цель – систематизировать и обобщить сведения о рациональных неравенствах, сформировать умение решать рациональные неравенства методом интервалов.
Корень степени п (20 часов, из них 1 контрольная работа)
Свойства функции у = х n , график функции у = хп, понятие корня степени п, корни чётной и нечётной степеней, арифметический корень, свойства корней степени п, корень степени п из натурального числа.
Основная цель – изучить свойства функции у = хп (на примере n=2 и n=3) и их графики, свойства корня степени n, выработать умение преобразовывать выражения, содержащие корни степени n.
Последовательности (21 часов, из них 2 контрольная работа)
Понятие числовой последовательности, арифметическая прогрессия, сумма п первых членов арифметической прогрессии, понятие геометрической прогрессии, сумма п первых членов геометрической прогрессии, бесконечно убывающая геометрической прогрессии
Основная цель – научить решать задачи, связанные с арифметической и геометрической прогрессиями.
Синус, косинус, тангенс и котангенс угла (20 часов, из них 2 контрольных работы ).
Понятие угла. Определение синуса. косинуса, тангенса и котангенса угла. Основные формулы для синуса, косинуса, тангенса и котангенса.
Основная цель — усвоить формулы косинуса и синуса суммы и разности двух углов, суммы и разности косинусов и синусов. Формулы для двойных и половинных углов; выработать умение выполнять тождественные преобразования тригонометрических выражений с использованием выведенных формул.
Приближенные вычисления (3 часов)
Абсолютная величина числа, абсолютная погрешность приближения, относительная погрешность приближения.
Основная цель – дать понятия абсолютной и относительной погрешности приближения, выработать умение выполнять оценку результатов вычислений.
Элементы комбинаторики и теории вероятности (8 часов, из них 1 контрольная работа)
Примеры комбинаторных задач, перестановки, размещения.
Основная цель – дать понятия комбинаторики, перестановки, размещения, научить решать связанные с ними задачи по нахождению числа объектов или их комбинаций, находить вероятность случайного события
Повторение (27 часов, из них 1 контрольная работа (итоговая)).
Календарно-тематическое планирование материала
| № | Тема урока |
|
|
|
-
| Повторение: функции и их графики |
|
|
|
-
| Повторение: решение уравнений и систем уравнений |
|
|
|
-
| Повторение: квадратный корень, упрощение выражений |
|
|
|
-
| Неравенства первой степени с одним неизвестным |
|
|
|
-
| Применение графиков функций к решению неравенств первой степени с одним неизвестным |
|
|
|
-
| Линейные неравенства с одним неизвестным |
|
|
|
-
| Решение неравенств сводящихся к линейным |
|
|
|
-
| Системы линейных неравенств с одним неизвестным. |
|
|
|
-
| Решение систем линейных неравенств с одним неизвестным. |
|
|
|
-
| Нахождение области определения функции или выражения |
|
|
|
-
| Нахождение наибольшего и наименьшего решений неравенства или системы. |
|
|
|
-
| Неравенства, содержащее неизвестное под знаком модуля |
|
|
|
-
| Понятие неравенства второй степени с одним неизвестным |
|
|
|
-
| Неравенства второй степени с положительным дискриминантом |
|
|
|
-
| Неравенства второй степени с дискриминантом равным нулю |
|
|
|
-
| Неравенства второй степени с отрицательным дискриминантом |
|
|
|
-
| Решение неравенств второй степени. |
|
|
|
-
| Нахождение области определения функции или выражения. |
|
|
|
-
| Неравенства, сводящиеся к неравенствам второй степени |
|
|
|
-
| Решение неравенств первой и второй степени с одним неизвестным |
|
|
|
-
| Контрольная работа № 1 по теме «Линейные и квадратные неравенства» |
|
|
|
-
| Анализ контрольной работы № 1. Метод интервалов. |
|
|
|
-
| Решение неравенств методом интервалов |
|
|
|
-
| Применение метода интервалов к решению неравенств |
|
|
|
-
| Рациональные неравенства |
|
|
|
-
| Решение рациональных неравенств |
|
|
|
-
| Решение рациональных неравенств методом интервалов |
|
|
|
-
| Системы рациональных неравенств |
|
|
|
-
| Решение систем рациональных неравенств |
|
|
|
-
| Нахождение области определения функции или выражения |
|
|
|
-
| Нестрогие неравенства |
|
|
|
-
| Решение нестрогих неравенств |
|
|
|
-
| Замена неизвестного при решении неравенств |
|
|
|
-
| Решение неравенств методом замены переменной |
|
|
|
-
| Доказательство числовых неравенств |
|
|
|
-
| Решение упражнений из сборников подготовки к ОГЭ |
|
|
|
-
| Контрольная работа № 2 по теме «Рациональные неравенства» |
|
|
|
-
| Анализ контрольной работы № 2. Функция у=хn (х≥0), её свойства и график. |
|
|
|
-
| Функция у=х2m, её свойства и график. |
|
|
|
-
| Функция у=х2m+1, её свойства и график. |
|
|
|
-
| Графическое решение уравнений и систем уравнений. |
|
|
|
-
| Наибольшее и наименьшее значения функции на промежутке. |
|
|
|
-
| Понятие корня степени n. |
|
|
|
-
| Корни чётной и нечётной степени. |
|
|
|
-
| Арифметический корень. |
|
|
|
-
| Нахождение значений выражений, содержащих корни степени n. |
|
|
|
-
| Свойства корней степени n. Вынесение множителя из-под знака корня. |
|
|
|
-
| Применение свойств корня к упрощению выражений. |
|
|
|
-
| Преобразование выражений с корнем n n-ой степени. |
|
|
|
-
| Вынесение и внесение буквенных множителей под знак корня степени n. |
|
|
|
-
| Функция у=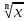 (х≥0), её свойства и график. (х≥0), её свойства и график. |
|
|
|
-
| Функция у=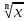 , её свойства и график , её свойства и график |
|
|
|
-
| Корень степени из натурального числа. Иррациональные уравнения. |
|
|
|
-
| Контрольная работа № 3 по теме «Корень степени n». |
|
|
|
-
| Анализ контрольной работы № 3. Понятие степени с рациональным показателем и её свойства. |
|
|
|
-
| Упрощение выражений, содержащих степень с рациональным показателем. |
|
|
|
-
| Преобразование выражений, содержащих степень с рациональным показателем. |
|
|
|
-
| Понятие числовой последовательности. Способы задания числовых последовательностей. |
|
|
|
-
| Свойства числовых последовательностей. |
|
|
|
-
| Понятие арифметической прогрессии. |
|
|
|
-
| Формула n-го члена арифметической прогрессии. |
|
|
|
-
| Свойство арифметической прогрессии. |
|
|
|
-
| Сумма первых n членов арифметической прогрессии. |
|
|
|
-
| Использование формулы первых n членов арифметической прогрессии для решения упражнений. |
|
|
|
-
| Решение упражнений по теме «Арифметическая прогрессия». |
|
|
|
-
| Контрольная работа № 4 по теме «Арифметическая прогрессия». |
|
|
|
-
| Анализ контрольной работы № 4. Понятие геометрической прогрессии. |
|
|
|
-
| Формула n-го члена геометрической прогрессии. |
|
|
|
-
| Свойство геометрической прогрессии. |
|
|
|
-
| Применение формулы n-го члена геометрической прогрессии. |
|
|
|
-
| Сумма первых n членов геометрической прогрессии. |
|
|
|
-
| Формула суммы первых n членов геометрической прогрессии. |
|
|
|
-
| Применение формулы суммы первых n членов геометрической прогрессии. |
|
|
|
-
| Решение упражнений по теме «Геометрическая прогрессия» |
|
|
|
-
| Решение упражнений по теме «Прогрессия». |
|
|
|
-
| Бесконечно убывающая геометрическая прогрессия. Сумма бесконечно убывающей геометрической прогрессии. |
|
|
|
-
| Решение упражнений по теме «Прогрессия». |
|
|
|
-
| Контрольная работа № 5 «Геометрическая прогрессия». |
|
|
|
-
| Анализ контрольной работы № 5. Понятие угла. Угол поворота. |
|
|
|
-
| Градусная и радианная мера угла. |
|
|
|
-
| Определение синуса и косинуса. |
|
|
|
-
| Табличные значения синуса и косинуса. Вычисление значений тригонометрических выражений. |
|
|
|
-
| Основное тригонометрическое тождество. |
|
|
|
-
| Формулы приведения. |
|
|
|
-
| Упрощение тригонометрических выражений. |
|
|
|
-
| Тангенс и котангенс. Основные формулы для тангенса и котангенса. |
|
|
|
-
| Упрощение тригонометрических выражений. |
|
|
|
-
| Контрольная работа № 6 по теме «Тригонометрические выражения». |
|
|
|
-
| Анализ контрольной работы № 6. Косинус разности и косинус суммы двух углов. |
|
|
|
-
| Синус суммы и синус разности двух углов. |
|
|
|
-
| Упрощение выражений. |
|
|
|
-
| Сумма и разность синусов и косинусов. |
|
|
|
-
| Формулы двойных углов |
|
|
|
-
| Формулы половинных углов |
|
|
|
-
| Упрощение выражений. |
|
|
|
-
| Произведение синусов и косинусов. |
|
|
|
-
| Преобразование тригонометрических выражений. |
|
|
|
-
| Контрольная работа № 7 По теме «Формулы тригонометрии». |
|
|
|
-
| Анализ контрольной работы № 7. Абсолютная и относительная погрешность приближения. |
|
|
|
-
| Приближения суммы и разности. |
|
|
|
-
| Приближение произведения и частного. |
|
|
|
-
| Способы представления числовых данных. Характеристики числовых данных. |
|
|
|
-
| Задачи на перебор всех возможных вариантов. Комбинаторные правила. |
|
|
|
-
| Перестановки. Размещения. |
|
|
|
-
| Сочетания. |
|
|
|
-
| Случайные события. Вероятность случайного события. |
|
|
|
-
| Сумма, произведение и разность случайных событий. Несовместные и независимые события. |
|
|
|
-
| Частота случайных событий. |
|
|
|
-
| Контрольная работа № 8 по теме «Элементы приближённых вычислений, статистики, комбинаторики и теории вероятности» |
|
|
|
-
| Повторение: целые выражения и их упрощение. |
|
|
|
-
| Повторение: преобразование рациональных выражений. |
|
|
|
-
| Повторение: степень и её свойства. |
|
|
|
-
| Повторение: преобразование выражений, содержащих квадратные корни. |
|
|
|
-
| Повторение: решение уравнений. |
|
|
|
-
| Повторение: решение систем уравнений. |
|
|
|
-
| Повторение: решение неравенств. |
|
|
|
-
| Повторение: решение систем неравенств. |
|
|
|
-
| Повторение: прогрессии. |
|
|
|
-
| Повторение: основы теории вероятности. |
|
|
|
-
| Обобщающее повторение по всем темам алгебры |
|
|
|
-
| Обобщающее повторение по всем темам алгебры |
|
|
|
-
| Обобщающее повторение по всем темам алгебры |
|
|
|
-
| Обобщающее повторение по всем темам алгебры |
|
|
|
-
| Итоговая контрольная работа № 9 |
|
|
|
| 125-136 | Решение заданий из сборников подготовки к ОГЭ |
|
|
|





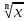 (х≥0), её свойства и график.
(х≥0), её свойства и график.



















