

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 14.08.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Рабочая программа 10-11 класс
УМК Мерзляк
Просмотр содержимого документа
«Рабочая программа 10-11 класс»
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Рабочая программа по учебному предмету «Алгебра и начала анализа» и геометрия составлена на основе федерального государственного образовательного стандарта среднего общего образования (ФГОС СОО), с учетом примерной программы по предмету, УМК М.: Вентана - Граф: Алгебра и начала анализа – А.Г. Мерзляка, Д.А. Номировского, В.Б. Полонского, М.С. Якира, Геометрия 10-11. Погорелов А.В. – 10-е издание. – М.: Просвещение, 2006 и определяет цель, задачи, планируемые результаты освоения программы учебного предмета «Алгебра и начала анализа» и геометрия, а также основное содержание указанного учебного предмета.
I. ПЛАНИРУЕМЫЕ ПРЕДМЕТНЫЕ РЕЗУЛЬТАТЫ ОСВОЕНИЯ
УЧЕБНОГО ПРЕДМЕТА «АЛГЕБРА И НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА» И ГЕОМЕТРИЯ
10 класс
Учащийся научится:
-
формулировать определения наибольшего и наименьшего значений функции, чётной и нечётной функций, обратимой функции, взаимно обратных функций, определения области определения уравнений (неравенств), равносильных уравнений (неравенств), уравнений-следствий (неравенств-следствий), постороннего корня;
-
формулировать теоремы о свойствах графиков чётных и нечётных функций,
-
находить наибольшее и наименьшее значения функции на множестве по её графику, исследовать функцию, заданную формулой, на чётность, строить графики функций, используя чётность или нечётность;
-
формулировать определение степенной функции с целым показателем, определение корня (арифметического корня) n-й степени, а также теоремы о его свойствах, определение степени с рациональным показателем, а также теоремы о её свойствах;
-
формулировать определение степенной функции с целым показателем;
-
описывать свойства степенной функции с целым показателем, выделяя случаи чётной и нечётной степени, а также натуральной, нулевой и целой отрицательной степени;
-
строить графики функций на основе графика степенной функции с целым показателем; находить наибольшее и наименьшее значения степенной функции с целым показателем на промежутке;
-
формулировать определение корня (арифметического корня) n-й степени, а также теоремы о его свойствах, выделяя случаи корней чётной и нечётной степени;
-
решать уравнения, сводящиеся к уравнению xn = a; выполнять тождественные преобразования выражений, содержащих корни n-й степени, в частности выносить множитель из-под знака корня n-й степени, вносить множитель под знак корня n-й степени, освобождаться от иррациональности в знаменателе дроби; описывать свойства функции, выделяя случаи корней чётной и нечётной степени.
-
формулировать определение степени с рациональным показателем, а также теоремы о её свойствах;
-
выполнять тождественные преобразования выражений, содержащих степени с рациональным показателем;
-
применять метод равносильных преобразований для решения уравнений и неравенств; находить область определения уравнений и неравенств;
-
применять метод следствий для решения уравнений;
-
решать неравенства методом интервалов;
-
формулировать определение радианной меры угла, определения косинуса, синуса, тангенса и котангенса угла поворота, определения периодической функции, формулы сложения, формулы приведения, формулы двойных углов.
-
находить радианную меру угла по его градусной мере и градусную меру угла по его радианной мере; вычислять длины дуг окружностей;
-
выяснять знак значений тригонометрических функций; упрощать тригонометрические выражения, используя свойства чётности тригонометрических функций;
-
формулировать определения периодической функции, её главного периода;
-
упрощать тригонометрические выражения, используя свойства периодичности тригонометрических функций; описывать свойства тригонометрических функций;
-
строить графики функций на основе графиков четырёх основных тригонометрических функций;
-
преобразовывать тригонометрические выражения на основе соотношений между тригонометрическими функциями одного и того же аргумента;
-
преобразовывать тригонометрические выражения на основе формул сложения; формул приведения, формул двойных и половинных углов, формул суммы и разности синусов (косинусов), формул преобразования произведения тригонометрических функций в сумму;
-
формулировать определения арккосинуса, арксинуса, арктангенса, арккотангенса, свойства обратных тригонометрических функций, метод разложения на множители;
-
находить значения обратных тригонометрических функций для отдельных табличных значений аргумента;
-
используя понятия арккосинуса, арксинуса, арктангенса, арккотангенса, решать простейшие тригонометрические уравнения.
-
формулировать свойства обратных тригонометрических функций;
-
строить графики функций на основе графиков четырёх основных обратных тригонометрических функций; упрощать выражения, содержащие обратные тригонометрические функции;
-
решать тригонометрические уравнения, сводящиеся к алгебраическим уравнениям, в частности решать однородные тригонометрические уравнения первой и второй степени, а также решать тригонометрические уравнения, применяя метод разложения на множители;
-
решать простейшие тригонометрические неравенства;
-
формулировать понятие производной функции, физического и геометрического смысла производной; производной степени, корня; правила дифференцирования; формулы производных элементарных функций; уравнение касательной к графику функции; алгоритм составления уравнения касательной; понятие стационарных, критических точек, точек экстремума;
-
применять производную к исследованию функций и построению графиков;
-
как исследовать в простейших случаях функции на монотонность, находить наибольшее и наименьшее значения функции;
-
находить интервалы возрастания и убывания функций;
-
строить эскиз графика непрерывной функции, определённой на отрезке;
-
находить стационарные точки функции, критические точки и точки экстремума;
-
применять производную к исследованию функций и построению графиков;
-
находить наибольшее и наименьшее значение функции;
11 класс
Учащийся научится:
-
решать показательные уравнения (неравенства); производить равносильные преобразования показательных уравнений (неравенств); решать показательные уравнения (неравенства), сводящиеся к алгебраическим;
-
решать логарифмические уравнения (неравенства); производить равносильные преобразования логарифмических уравнений (неравенств); решать логарифмические уравнения (неравенства), сводящиеся к алгебраическим;
-
решать алгебраические уравнения на множестве комплексных чисел; применять основную теорему алгебры;
-
строить и исследовать логарифмическую и показательную функции;
-
исследовать первообразную функции; общий вид первообразных; неопределённый интеграл; пользоваться таблицей первообразных функций; использовать правила нахождения первообразной функции; определённый интеграл; формулу Ньютона — Лейбница; методы нахождения площади фигур и объёма тел, ограниченных данными линиями и поверхностями;
-
распознавать вероятностные эксперименты, описываемые с помощью схемы Бернулли; находить вероятность события, состоящего в том, что в схеме Бернулли успехом завершится данное количество испытаний;
-
формулировать определения случайной величины и множества её значений; для случайной величины с конечным множеством значений формулировать определения распределения случайной величины и её математического ожидания; находить математическое ожидание случайной величины по её распределению; использовать выводы теории вероятностей в задачах с практическим жизненным содержанием;
-
Формулировать определение сочетания n-элементного множества по k элементов; используя формулы: количества перестановок конечного множества, размещений n-элементного множества по k элементов и сочетаний n-элементного множества по k элементов, решать задачи комбинаторного характера;
-
записывать формулу бинома Ньютона.
В результате изучения курса геометрии учащиеся 10-11 классов должны
-
понимать, что геометрические формы являются идеализированными образами реальных объектов; научиться использовать геометрический язык для описания предметов окружающего мира; получить представление о некоторых областях применения геометрии в быту, науке, технике, искусстве;
-
соотносить плоские геометрические фигуры и трехмерные объекты с их описаниями, чертежами, изображениями; различать и анализировать взаимное расположение фигур;
-
изображать геометрические фигуры и тела, выполнять чертеж по условию задачи;
-
понимать стереометрические чертежи;
-
решать геометрические задачи, опираясь на изученные свойства планиметрических и стереометрических фигур и отношений между ними, применяя алгебраический и тригонометрический аппарат;
-
проводить доказательные рассуждения при решении задач, доказывать основные теоремы курса;
-
вычислять линейные элементы и углы в пространственных конфигурациях, объемы и площади поверхностей пространственных тел и их простейших комбинаций;
-
применять координатно-векторный метод для вычисления отношений, расстояний и углов;
-
анализировать в простейших случаях взаимное расположение объектов в пространстве;
-
строить сечения многогранников и изображать сечения тел вращения.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур;
-
вычисления длин, площадей и объемов реальных объектов при решении практических задач, используя при необходимости справочники и вычислительные устройства.
Система оценки планируемых результатов осуществляется в следующих формах и видах контроля:
Оценка индивидуального проекта.
Для оценки индивидуального проекта используются следующие критерии:
-
способность к самостоятельному приобретению знаний и решению проблем, проявляющаяся в умении поставить проблему и выбрать адекватные способы ее решения;
-
cформированность предметных знаний и способов действий, проявляющаяся в умении раскрывать содержание работы.
-
cформированность регулятивных действий, проявляющаяся в умении самостоятельно планировать и управлять своей познавательной деятельностью во времени.
Оценка индивидуальных достижений:
В портфолио войдут такие достижения обучающегося как:
-
Результаты участия во всероссийских олимпиадах школьников по математике;
-
Результаты участия в международных конкурсах;
-
Результаты участия в дистанционных олимпиадах;
-
Результаты участия в творческих конкурсах по предмету;
-
Результаты выполнения проектной деятельности;
ПЛАНИРУЕМЫЕ ЛИЧНОСТНЫЕ РЕЗУЛЬТАТЫ ОСВОЕНИЯ
УЧЕБНОГО ПРЕДМЕТА «АЛГЕБРА И НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА» И ГЕОМЕТРИЯ
Учащиеся получат возможность:
1) осознать свою российскую гражданскую идентичность
2)сформировать гражданскую позицию как активного и ответственного члена российского общества
3)быть готовыми к служению Отечеству, его защите;
4) сформируют мировоззрение
5) сформировать основы саморазвития и самовоспитания
6) научиться толерантно осознавать свое поведение в поликультурном мире
7) получить навыки сотрудничества со сверстниками, детьми младшего возраста, взрослыми
8) нравственного сознания и поведения
9)быть готовыми и способными к образованию, в том числе самообразованию
10) эстетически относиться к миру
11) принимать и реализовывать ценности здорового и безопасного образа жизни
12) научиться бережно, ответственно и компетентно относиться к физическому и психологическому здоровью
13) осознанно выбрать будущую профессию и возможность реализации собственных жизненных планов
14) сформировать экологическое мышление
15) ответственно относиться к учебе, выбору будущей профессии
ПЛАНИРУЕМЫЕ МЕТАПРЕДМЕТНЫЕ РЕЗУЛЬТАТЫ ОСВОЕНИЯ
УЧЕБНОГО ПРЕДМЕТА «АЛГЕБРА И НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА» И ГЕОМЕТРИЯ
Учащиеся получат возможность:
1) овладеть умением самостоятельно определять цели деятельности и составлять планы деятельности
2) научиться продуктивно общаться и взаимодействовать в процессе совместной деятельности
3) овладеть навыками познавательной, учебно -исследовательской и проектной деятельности
4) подготовиться и быть способными к самостоятельной информационно - познавательной деятельности
5)овладеть умением использовать средства информационных и коммуникационных технологий
6) научиться определять назначение и функции различных социальных институтов;
7) уметь самостоятельно оценивать и принимать решения, определяющие стратегию поведения
8) овладеть языковыми средствами
9) овладеть навыками познавательной рефлексии
II. СОДЕРЖАНИЕ УЧЕБНОГО ПРЕДМЕТА «АЛГЕБРА И НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА»
10 класс (170 часов)
ПОВТОРЕНИЕ И РАСШИРЕНИЕ СВЕДЕНИЙ О ФУНКЦИИ
Наибольшее и наименьшее значения функции. Построение графиков функций с помощью геометрических преобразований. Обратная функция. Свойства взаимно обратных функций Равносильные уравнения и неравенства. Решение уравнений и неравенств Метод интервалов. Применение метода интервалов для решения неравенств.
СТЕПЕННАЯ ФУНКЦИЯ
Анализ контрольной работы. Степенная функция с натуральным показателем. Степенная функция с целым показателем. Свойства степенной функции с целым показателем. Определение корня n-ой степени. Функция y= 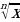 . Свойства корня n-й степени. Применение свойств корня n-ой степени при решении задач. Определение и свойства степени с рациональным показателем. Применение свойств степени при решении задач. Иррациональные уравнения. Решение иррациональных уравнений. Иррациональные уравнения. Метод равносильных преобразований для решения иррациональных уравнений. Различные методы решения иррациональных уравнений. Иррациональные неравенства.
. Свойства корня n-й степени. Применение свойств корня n-ой степени при решении задач. Определение и свойства степени с рациональным показателем. Применение свойств степени при решении задач. Иррациональные уравнения. Решение иррациональных уравнений. Иррациональные уравнения. Метод равносильных преобразований для решения иррациональных уравнений. Различные методы решения иррациональных уравнений. Иррациональные неравенства.
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
Радианная мера угла. Градусная мера угла. Радианная мера угла. Тригонометрические функции числового аргумента. Углы поворота косинуса, синуса, тангенса и котангенса. Знаки значений тригонометрических функций. Четность и нечетность тригонометрических функций. Периодические функции. Свойства функций y = sin x и y = cos x. Графики функций y = sin x и y = cos x. Свойства функций y = tg x и y = ctg x. Графики функций y = tg x и y = ctg x. Основные соотношения между тригонометрическими функциями одного и того же аргумента. Формулы, демонстрирующие основные соотношения между тригонометрическими функциями одного и того же аргумента. Формулы сложения. Упрощение выражений, применяя формулы сложения. Формулы приведения. Правила применения формул приведения. Формулы двойного угла. Формулы половинного угла. Упрощение выражений, применяя формулы двойного и половинного аргумента. Сумма и разность синусов. Сумма и разность косинусов. Формулы преобразования произведения тригонометрических функций в сумму.
ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
Уравнение cos x = b. Решение уравнений вида cos x = b.Уравнение sin x = b.Решение уравнений вида sin x = b.Уравнения tg x = b и ctg x = b.Функции y = arccos x, y = arcsin x.Функции y = arctg x и y = arcctg x. Тригонометрические уравнения, сводящиеся к алгебраическим. Решение тригонометрических уравнений. Алгоритмы решения тригонометрических уравнений , сводящихся к алгебраическим. Решение тригонометрических уравнений методом разложения на множители. Применение разложения на множители при решении уравнений. Решение простейших тригонометрических неравенств.
ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
Представление о пределе функции в точке и о непрерывности функции в точке. Предел функции в точке. Задачи о мгновенной скорости и касательной к графику функции. Понятие производной. Дифференцируемая функция. Нахождение производной, используя предел разностного отношения. Правила вычисления производной. Производная суммы, произведения, частного, сложной функции. Применение производной суммы, произведения, частного для вычисления производной функции. Уравнение касательной. Геометрический смысл производной. Признаки возрастания и убывания функции. Применение производной для исследования функции на монотонность. Точки экстремума функции. Признаки точек минимума и максимума функции. Необходимые и достаточные условия экстремума. Применение производной при нахождении наибольшего и наименьшего значений функции. Нахождение наименьшего и наибольшего значений функции на промежутке. Построение графиков функций. План исследования графиков функции. Применение производной для построения графиков функций.
ПОВТОРЕНИЕ И СИСТЕМАТИЗАЦИЯ УЧЕБНОГО МАТЕРИАЛА
Решение задач по темам: функция, степенная функция, тригонометрические функции, тригонометрические уравнения и неравенства, производная и ее применение.
ИЗБРАННЫЕ ВОПРОСЫ ПЛАНИМЕТРИИ
Решение треугольников. Метрические соотношения в окружности. Свойства и признаки вписанных и описанных четырехугольников.
АКСИОМЫ ПЛАНИМЕТРИИ И ИХ ПРОСТЕЙШИЕ СЛЕДСТВИЯ
Аксиомы стереометрии. Существование плоскости, проходящей через данную прямую и данную точку. Пересечение прямой с плоскостью. Существование плоскости, проходящей через три данные точки
ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Параллельные прямые в пространстве. Признак параллельности прямых. Признак параллельности прямой и плоскости. Признак параллельности плоскостей. Существование плоскости, параллельной данной плоскости. Свойства параллельных плоскостей. Параллельное проектирование. Изображение пространственных фигур на плоскости.
ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Перпендикулярность прямых в пространстве. Признак перпендикулярности прямой и плоскости. Построение перпендикулярных прямой и плоскости. Свойства перпендикулярных прямой и плоскости. Перпендикуляр и наклонная. Теорема о трех перпендикулярах. Признак перпендикулярности плоскостей. Расстояние между скрещивающимися прямыми.
ДЕКАРТОВЫ КООРДИНАТЫ И ВЕКТОРЫ В ПРОСТРАНСТВЕ
Введение декартовых координат в пространстве. Расстояние между точками. Преобразование симметрии в пространстве. Симметрия в природе и на практике.
Угол между скрещивающимися прямыми. Угол между прямой и плоскостью
Угол между плоскостями. Площадь ортогональной проекции многоугольника. Уравнение сферы и плоскости. Формула расстояния от точки до плоскости.
Векторы в пространстве (модуль вектора, равенство векторов, угол между векторами). Действия над векторами в пространстве (сложение векторов, умножение векторов на число, скалярное произведение векторов). Коллинеарные векторы, Разложение вектора по двум неколлинеарным векторам. Компланарные векторы. Разложение вектора по трем некомпланарным.
ПОВТОРЕНИЕ
Решение задач по темам: параллельность и перпендикулярность прямых и плоскостей, декартовы координаты и векторы в пространстве.
11 класс (165 часов)
ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ
Степень с произвольным действительным показателем. Показательная функция. Показательные уравнения. Показательные неравенства. Логарифм и его свойства. Логарифмическая функция и ее свойства. Логарифмические уравнения. Логарифмические неравенства. Производные показательной и логарифмической функции.
ИНТЕГРАЛ И ЕГО ПРИМЕНЕНИЕ
Первообразная. Правила нахождения первообразной. Площадь криволинейной трапеции. Определенный интеграл. Вычисление объемов тел.
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ И БИНОМ НЬЮТОНА
Метод математической индукции. Перестановки, размещения. Сочетания (комбинации). Бином Ньютона.
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТИ
Операции над событиями. Зависимые и независимые события. Схема Бернулли. Случайные величины и их характеристики.
ПОВТОРЕНИЕ КУРСА АЛГЕБРЫ И НАЧАЛ АНАЛИЗА
Повторение курса алгебры и начал математического анализа.
МНОГОГРАННИКИ
Двугранный и многогранный углы. Линейный угол двугранного угла. Многогранники. Сечения многогранников. Призма. Прямая и правильная призмы. Параллелепипед. Пирамида. Усеченная пирамида. Правильная пирамида. Правильные многогранники.
ТЕЛА ВРАЩЕНИЯ
Тела вращения: цилиндр, конус, шар. Сечения тел вращения. Касательная плоскость к шару. Вписанные и описанные многогранники. Понятие тела и его поверхности в геометрии.
ОБЪЕМЫ МНОГОГРАННИКОВ
Понятие об объеме. Объемы многогранников: прямоугольного и наклонного параллелепипедов, призмы, пирамиды. Равновеликие тела. Объемы подобных тел.
ОБЪЕМЫ И ПОВЕРХНОСТИ ТЕЛ ВРАЩЕНИЯ
Объем цилиндра, конуса, шара. Объем шарового сегмента и сектора. Понятие площади поверхности. Площади боковых поверхностей цилиндра и конуса, площадь сферы.
ПОВТОРЕНИЕ КУРСА ГЕОМЕТРИИ
Повторение курса геометрии 11класса.
III. ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ УЧЕБНОГО ПРЕДМЕТА
«АЛГЕБРА И НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА»
10 КЛАСС
| Тематический раздел/ часы | Содержание (КЭС) | Планируемые результаты | Формы и методы оценки достижения/ КИМ | ||||
| Личностные | Метапред-метные | Предметные | |||||
| Ученик научится | Ученик получит возможность научиться | ||||||
| Тема 1. Повторение и расширение сведений о функции | Наибольшее и наименьшее значения функции. Построение графиков функций с помощью геометрических преобразований. Обратная функция. Свойства взаимно обратных функций Равносильные уравнения и неравенства. Решение уравнений и неравенств Метод интервалов. Применение метода интервалов для решения неравенств. | Принятие и освоение социальной роли обучающегося, развитие мотивов учебной деятельности и формирование личностного смысла учения | Использование знаково-символических средств представления информации для создания моделей изучаемых объектов и процессов, схем решения учебных и практических задач. Умение работать в материальной и информационной среде начального общего образования (в том числе с учебными моделями) в соответствии с содержанием конкретного учебного предмета
| приобретение начального опыта применения математических знаний для решения учебно-познавательных и учебно-практических задач | использование начальных математических знаний для описания и объяснения окружающих предметов, процессов, явлений, а также оценки их количественных и пространственных отношений | КР-1. Повторение и расширение сведений о функции | |
| Тема 2. Степенная функция | Анализ контрольной работы. Степенная функция с натуральным показателем. Степенная функция с целым показателем. Свойства степенной функции с целым показателем. Определение корня n-ой степени. Функция y= | Принятие и освоение социальной роли обучающегося, развитие мотивов учебной деятельности и формирование личностного смысла учения | Формирование умения планировать, контролировать и оценивать учебные действия в соответствии с поставленной задачей и условиями ее реализации; определять наиболее эффективные способы достижения результата. | умение выполнять устно и письменно арифметические действия с числами и числовыми выражениями | умение выполнять устно и письменно арифметические действия с числами и числовыми выражениями, решать текстовые задачи, умение действовать в соответствии с алгоритмом и строить простейшие алгоритмы | КР-2. Степенная функция. Корень n-й степени и его свойства. | |
| Тема 3. Тригонометрические функции | Радианная мера угла. Градусная мера угла. Радианная мера угла. Тригонометрические функции числового аргумента. Углы поворота косинуса, синуса, тангенса и котангенса. Знаки значений тригонометрических функций. Четность и нечетность тригонометрических функций. Периодические функции. Свойства функций y = sin x и y = cos x. Графики функций y = sin x и y = cos x. Свойства функций y = tg x и y = ctg x. Графики функций y = tg x и y = ctg x. Основные соотношения между тригонометрическими функциями одного и того же аргумента. Формулы, демонстрирующие основные соотношения между тригонометрическими функциями одного и того же аргумента. Формулы сложения. Упрощение выражений, применяя формулы сложения. Формулы приведения. Правила применения формул приведения. Формулы двойного угла. Формулы половинного угла. Упрощение выражений, применяя формулы двойного и половинного аргумента. Сумма и разность синусов. Сумма и разность косинусов. Формулы преобразования произведения тригонометрических функций в сумму. | Принятие и освоение социальной роли обучающегося, развитие мотивов учебной деятельности и формирование личностного смысла учения | Освоение способов решения проблем творческого и поискового характера | использование начальных математических знаний для описания и объяснения окружающих предметов, процессов, явлений | оценка количественных и пространственных отношений окружающих предметов, процессов, явлений | КР-4. Тригонометрические функции и их свойства.
| |
| Тема 4 .Тригонометрические уравнения и неравенства | Уравнение cos x = b. Решение уравнений вида cos x = b.Уравнение sin x = b.Решение уравнений вида sin x = b.Уравнения tg x = b и ctg x = b.Функции y = arccos x, y = arcsin x.Функции y = arctg x и y = arcctg x. Тригонометрические уравнения, сводящиеся к алгебраическим. Решение тригонометрических уравнений. Алгоритмы решения тригонометрических уравнений , сводящихся к алгебраическим. Решение тригонометрических уравнений методом разложения на множители. Применение разложения на множители при решении уравнений. Решение простейших тригонометрических неравенств. | Принятие и освоение социальной роли обучающегося, развитие мотивов учебной деятельности и формирование личностного смысла учения | Формирование умения понимать причины успеха/неуспеха учебной деятельности и способности конструктивно действовать даже в ситуациях неуспеха | умение выполнять устно и письменно арифметические действия с числами и числовыми выражениями, решать текстовые задачи, умение действовать в соответствии с алгоритмом и строить простейшие алгоритмы | исследовать, распознавать и изображать графики тригонометрическихфункции, работать с таблицами, схемами, графиками, представлять, анализировать и интерпретировать данные; | КР-6. Тригонометрические уравнения и неравенства.
| |
| Тема 5. Производная и ее применение | Представление о пределе функции в точке и о непрерывности функции в точке. Предел функции в точке. Задачи о мгновенной скорости и касательной к графику функции. Понятие производной. Дифференцируемая функция. Нахождение производной, используя предел разностного отношения. Правила вычисления производной. Производная суммы, произведения, частного, сложной функции. Применение производной суммы, произведения, частного для вычисления производной функции. Уравнение касательной. Геометрический смысл производной. Признаки возрастания и убывания функции. Применение производной для исследования функции на монотонность. Точки экстремума функции. Признаки точек минимума и максимума функции. Необходимые и достаточные условия экстремума. Применение производной при нахождении наибольшего и наименьшего значений функции. Нахождение наименьшего и наибольшего значений функции на промежутке. Построение графиков функций. План исследования графиков функции. Применение производной для построения графиков функций. | Овладение начальными навыками адаптации в динамично изменяющемся и развивающемся мире | Овладение способностью принимать и сохранять цели и задачи учебной деятельности, поиска средств ее осуществления | использование начальных математических знаний для описания и объяснения окружающих предметов, процессов, явлений | овладение основами логического и алгоритмического мышления, пространственного воображения и математической речи, измерения, пересчета, прикидки и оценки, наглядного представления данных и процессов, записи и выполнения алгоритмов | КР-7. Производная. Уравнение касательной КР-8. Применение производной | |
| Повторение и систематизация учебного материала | Решение задач по темам: функция, степенная функция, тригонометрические функции, тригонометрические уравнения и неравенства, производная и ее применение. | Принятие и освоение социальной роли обучающегося, развитие мотивов учебной деятельности и формирование личностного смысла учения | Формирование умения планировать, контролировать и оценивать учебные действия в соответствии с поставленной задачей и условиями ее реализации; определять наиболее эффективные способы достижения результата | умение выполнять устно и письменно арифметические действия с числами и числовыми выражениями, решать текстовые задачи, умение действовать в соответствии с алгоритмом и строить простейшие алгоритмы, исследовать, распознавать и изображать геометрические фигуры, работать с таблицами, схемами, графиками и диаграммами, цепочками, совокупностями | представлять, анализировать и интерпретировать данные | КР-9. Обобщение и систематизация знаний учащихся | |
| Избранные вопросы планиметрии | Решение треугольников. Метрические соотношения в окружности. Свойства и признаки вписанных и описанных четырехугольников. | Развитие этических чувств, доброжелательности и эмоционально-нравственной отзывчивости, понимания и сопереживания чувствам других людей | Использование знаково-символических средств представления информации для создания моделей изучаемых объектов и процессов, схем решения учебных и практических задач. Умение работать в материальной и информационной среде начального общего образования (в том числе с учебными моделями)
| овладение основами логического и алгоритмического мышления, пространственного воображения и математической речи, измерения | Приобрести умение действовать в соответствии с алгоритмом, исследовать геометрические фигуры, представлять, анализировать и интерпретировать данные | Входная контрольная работа | |
| Аксиомы стереометрии и их простейшие следствия | Аксиомы стереометрии. Существование плоскости, проходящей через данную прямую и данную точку. Пересечение прямой с плоскостью. Существование плоскости, проходящей через три данные точки
| Формирование уважительного отношения к иному мнению | отбор источников информации для поиска нового знания | использование математических знаний для описания и объяснения окружающих предметов, процессов, явлений | приобрести опыт применения математических знаний для решения учебно-познавательных и учебно-практических задач | Контрольная работа № 1 | |
| Параллельность прямых и плоскостей | Параллельные прямые в пространстве. Признак параллельности прямых. Признак параллельности прямой и плоскости. Признак параллельности плоскостей. Существование плоскости, параллельной данной плоскости. Свойства параллельных плоскостей. Параллельное проектирование. Изображение пространственных фигур на плоскости. | Развитие самостоятельности и личной ответственности за свои поступки, в том числе в информационной деятельности, на основе представлений о нравственных нормах, социальной справедливости и свободе | Освоение способов решения проблем творческого и поискового характера | соотносить плоские геометрические фигуры и трехмерные объекты с их описаниями, чертежами, изображениями; различать и анализировать взаимное расположение фигур | Научиться исследовать (моделировать) несложные практические ситуации на основе изученных формул и свойств фигур | Контрольная работа № 2 | |
| Перпендикулярность прямых и плоскостей | Перпендикулярность прямых в пространстве. Признак перпендикулярности прямой и плоскости. Построение перпендикулярных прямой и плоскости. Свойства перпендикулярных прямой и плоскости. Перпендикуляр и наклонная. Теорема о трех перпендикулярах. Признак перпендикулярности плоскостей. Расстояние между скрещивающимися прямыми. | Развитие навыков сотрудничества со взрослыми и сверстниками в разных социальных ситуациях, умения не создавать конфликтов и находить выходы из спорных ситуаций | Освоение форм познавательной и личностной рефлексии | изображать геометрические фигуры и тела, выполнять чертеж по условию задачи | Использовать приобретенные знания и умения в практической деятельности и повседневной жизни | Контрольная работа № 3 | |
| Декартовы координаты и векторы в пространстве | Введение декартовых координат в пространстве. Расстояние между точками. Преобразование симметрии в пространстве. Симметрия в природе и на практике. Угол между скрещивающимися прямыми. Угол между прямой и плоскостью Угол между плоскостями. Площадь ортогональной проекции многоугольника. Уравнение сферы и плоскости. Формула расстояния от точки до плоскости. Векторы в пространстве (модуль вектора, равенство векторов, угол между векторами). Действия над векторами в пространстве (сложение векторов, умножение векторов на число, скалярное произведение векторов). Коллинеарные векторы, Разложение вектора по двум неколлинеарным векторам. Компланарные векторы. Разложение вектора по трем некомпланарным. | Принятие и освоение социальной роли обучающегося, развитие мотивов учебной деятельности и формирование личностного смысла учения | Использование знаково-символических средств представления информации для создания моделей изучаемых объектов и процессов, схем решения учебных и практических задач | применять координатно-векторный метод для вычисления отношений, расстояний и углов | Использовать приобретенные знания и умения в практической деятельности и повседневной жизни | Контрольная работа № 4 | |
| Повторение | Решение задач по темам: параллельность и перпендикулярность прямых и плоскостей, декартовы координаты и векторы в пространстве. | Принятие и освоение социальной роли обучающегося, развитие мотивов учебной деятельности и формирование личностного смысла учения | Использование знаково-символических средств представления информации для создания моделей изучаемых объектов и процессов, схем решения учебных и практических задач | анализировать в простейших случаях взаимное расположение объектов в пространстве | Использовать приобретенные знания и умения в практической деятельности и повседневной жизни | Итоговая контрольная работа по геометрии 10 класс
| |
11 КЛАСС
| Тематический раздел/ часы | Содержание (КЭС) | Планируемые результаты | Формы и методы оценки достижения/ КИМ | |||
| Личностные | Метапред-метные | Предметные | ||||
| Ученик научится | Ученик получит возможность научиться | |||||
| Тема 1. Показательная и логарифмическая функции | Степень с произвольным действительным показателем. Показательная функция. Показательные уравнения. Показательные неравенства. Логарифм и его свойства. Логарифмическая функция и ее свойства. Логарифмические уравнения. Логарифмические неравенства. Производные показательной и логарифмической функции. | Принятие и освоение социальной роли обучающегося, развитие мотивов учебной деятельности и формирование личностного смысла учения | Овладение способностью принимать и сохранять цели и задачи учебной деятельности, поиска средств ее осуществления | решать показательные и логарифмические уравнения (неравенства); производить равносильные преобразования показательных уравнений (неравенств); решать показательные уравнения (неравенства), сводящиеся к алгебраическим | строить и исследовать логарифмическую и показательную функции | Контрольная работа № 1 |
| Тема 2. Интеграл и его применение | Первообразная. Правила нахождения первообразной. Площадь криволинейной трапеции. Определенный интеграл. Вычисление объемов тел. | Овладение начальными навыками адаптации в динамично изменяющемся и развивающемся мире | Освоение способов решения проблем творческого и поискового характера | исследовать первообразную функции; общий вид первообразных; неопределённый интеграл; пользоваться таблицей первообразных функций; использовать правила нахождения первообразной функции; определённый интеграл; формулу Ньютона — Лейбница; | Использовать методы нахождения площади фигур и объёма тел, ограниченных данными линиями и поверхностями при решении практических задач | Контрольная работа № 2 |
| Тема 3. Элементы комбинаторики и бином Ньютона | Метод математической индукции. Перестановки, размещения. Сочетания (комбинации). Бином Ньютона. | Развитие самостоятельности и личной ответственности за свои поступки, в том числе в информационной деятельности, на основе представлений о нравственных нормах, социальной справедливости и свободе | Формирование умения планировать, контролировать и оценивать учебные действия в соответствии с поставленной задачей и условиями ее реализации; определять наиболее эффективные способы достижения результата | распознавать вероятностные эксперименты, описываемые с помощью схемы Бернулли; находить вероятность события, состоящего в том, что в схеме Бернулли успехом завершится данное количество испытаний | Научиться решать задачи повышенного уровня сложности | Контрольная работа № 3 |
| Тема 4. Элементы теории вероятности | Операции над событиями. Зависимые и независимые события. Схема Бернулли. Случайные величины и их характеристики. | Формирование эстетических потребностей, ценностей и чувств | Формирование умения понимать причины успеха/неуспеха учебной деятельности и способности конструктивно действовать даже в ситуациях неуспеха | формулировать определения случайной величины и множества её значений; для случайной величины с конечным множеством значений формулировать определения распределения случайной величины и её математического ожидания; находить математическое ожидание случайной величины по её распределению; | использовать выводы теории вероятностей в задачах с практическим жизненным содержанием | Контрольная работа № 4 |
| Повторение курса алгебры и начал математического анализа | Повторение курса алгебры и начал математического анализа | Развитие навыков сотрудничества со взрослыми и сверстниками в разных социальных ситуациях, умения не создавать конфликтов и находить выходы из спорных ситуаций | Использование знаково-символических средств представления информации для создания моделей изучаемых объектов и процессов, схем решения учебных и практических задач.
| Формулировать и доказывать логичность выбранного метода решения задачи | использовать выводы теории в задачах с практическим жизненным содержанием | Итоговая контрольная работа |
| Многогранники | Двугранный и многогранный углы. Линейный угол двугранного угла. Многогранники. Сечения многогранников. Призма. Прямая и правильная призмы. Параллелепипед. Пирамида. Усеченная пирамида. Правильная пирамида. Правильные многогранники. | Развитие навыков сотрудничества со взрослыми и сверстниками в разных социальных ситуациях, умения не создавать конфликтов и находить выходы из спорных ситуаций | Умение работать в материальной и информационной среде общего образования (в том числе с учебными моделями)
| соотносить плоские геометрические фигуры и трехмерные объекты с их описаниями, чертежами, изображениями; | различать и анализировать взаимное расположение фигур | Контрольная работа № 1,2 |
| Тела вращения | Тела вращения: цилиндр, конус, шар. Сечения тел вращения. Касательная плоскость к шару. Вписанные и описанные многогранники. Понятие тела и его поверхности в геометрии. | Развитие самостоятельности и личной ответственности за свои поступки, в том числе в информационной деятельности, на основе представлений о нравственных нормах, социальной справедливости и свободе | Овладение способностью принимать и сохранять цели и задачи учебной деятельности, поиска средств ее осуществления | решать геометрические задачи, опираясь на изученные свойства планиметрических и стереометрических фигур и отношений между ними, применяя алгебраический и тригонометрический аппарат | различать и анализировать взаимное расположение фигур | Контрольная работа № 3 |
| Объёмы многогранников | Понятие об объеме. Объемы многогранников: прямоугольного и наклонного параллелепипедов, призмы, пирамиды. Равновеликие тела. Объемы подобных тел. | Формирование целостного, социально ориентированного взгляда на мир в его органичном единстве и разнообразии природы, народов, культур и религий. Формирование уважительного отношения к иному мнению, истории и культуре других народов | Формирование умения планировать, контролировать и оценивать учебные действия в соответствии с поставленной задачей и условиями ее реализации; определять наиболее эффективные способы достижения результата | применять координатно-векторный метод для вычисления отношений, расстояний и углов; анализировать в простейших случаях взаимное расположение объектов в пространстве;
| строить сечения многогранников и изображать сечения тел вращения.
| Контрольная работа № 4 |
| Объёмы и поверхности тел вращения | Объем цилиндра, конуса, шара. Объем шарового сегмента и сектора. Понятие площади поверхности. Площади боковых поверхностей цилиндра и конуса, площадь сферы. | Формирование эстетических потребностей, ценностей и чувств | Формирование умения понимать причины успеха/неуспеха учебной деятельности и способности конструктивно действовать даже в ситуациях неуспеха | понимать стереометрические чертежи | Выполнять вычисления длин, площадей и объемов реальных объектов при решении практических задач, используя при необходимости справочники и вычислительные устройства | Контрольная работа № 5 |
| Повторение. | Повторение курса геометрии 11класса. | Формирование установки на безопасный, здоровый образ жизни, наличие мотивации к творческому труду, работе на результат, бережному отношению к материальным и духовным ценностям | Овладение логическими действиями сравнения, анализа, синтеза, обобщения, классификации по родовидовым признакам, установления аналогий и причинно-следственных связей, построения рассуждений, отнесения к известным понятиям | решать геометрические задачи, опираясь на изученные свойства планиметрических и стереометрических фигур и отношений между ними, применяя алгебраический и тригонометрический аппарат | Выполнять вычисления длин, площадей и объемов реальных объектов при решении практических задач, используя при необходимости справочники и вычислительные устройства | Контрольная работа № 6 |
КИМ 10 класс. Повторение и расширение сведений о функции КР-1. Вариант 1,2
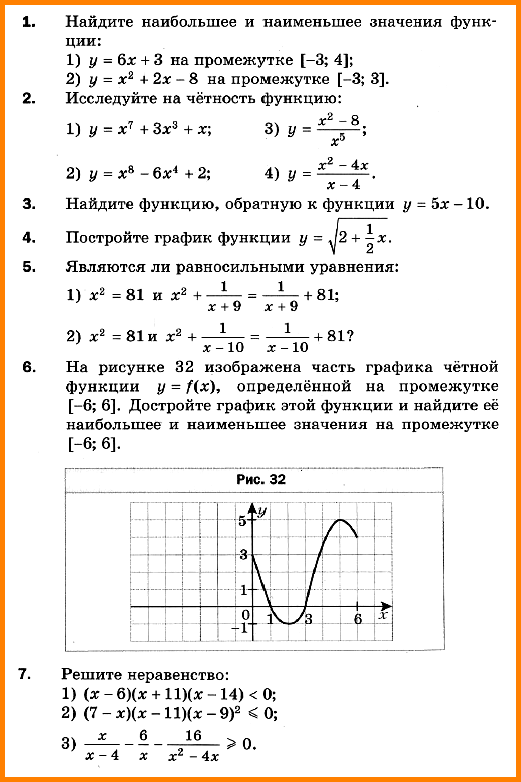
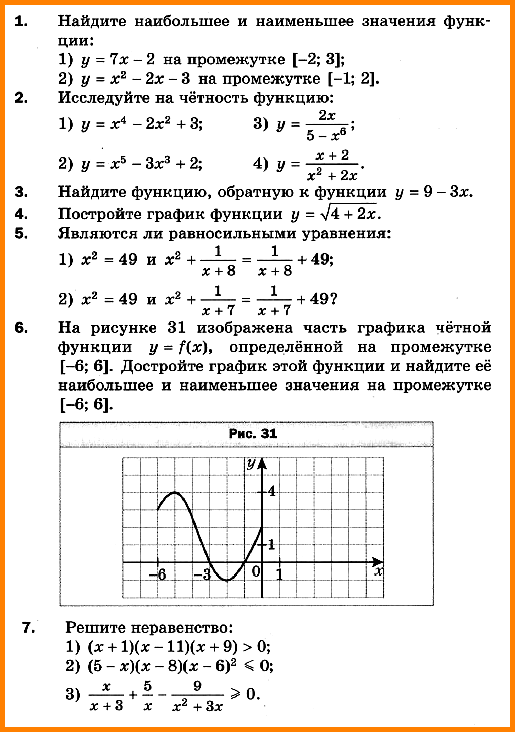
К Р-2. Степенная функция. Корень n-й степени и его свойства.
Р-2. Степенная функция. Корень n-й степени и его свойства.

Кр-3. Степень с рациональным показателем и её свойства. Иррациональные уравнения и неравенства


К
 Р 4. Тригонометрические функции и их свойства.
Р 4. Тригонометрические функции и их свойства.
К Р 5. Соотношение между тригонометрическими функциями одного и того же аргумента. Формулы сложения и их следствия
Р 5. Соотношение между тригонометрическими функциями одного и того же аргумента. Формулы сложения и их следствия

К
 Р 6. Тригонометрические уравнения и неравенства
Р 6. Тригонометрические уравнения и неравенства
К
 Р 7. Производная. Уравнение касательной.
Р 7. Производная. Уравнение касательной.
КР 8. Применение производной
К
 Р 9. Обобщение и систематизация знаний учащихся
Р 9. Обобщение и систематизация знаний учащихся


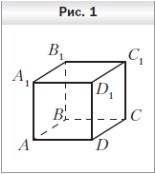
Контрольная работа № 1 по теме «Аксиомы стереометрии и следствия из них. Начальные представления о многогранниках»
В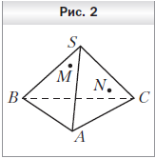 ариант 1
ариант 1
1. На рисунке 1 изображён куб ABCDA1B1C1D1. Укажите прямую пересечения плоскостей A1DC и BB1C1.
2. Даны точки A, B и C такие, что AB = 12 см, BC = 19 см,
AC = 7 см. Сколько плоскостей можно провести через точки A, B и C? Ответ обоснуйте.
3 . Плоскость α проходит через вершины A и D параллелограмма ABCD и точку O пересечения его диагоналей. Докажите, что прямая BC лежит в плоскости α.
4. Точки M и N принадлежат соответственно граням SAB и SAC пирамиды SABC (рис. 2). Постройте точку пересечения прямой MN с плоскостью ABC.
5. Постройте сечение пирамиды SABC плоскостью, проходящей через точки D, E и F, принадлежащие соответственно рёбрам AB, BC и SC, причём прямые DE и AC не параллельны.
В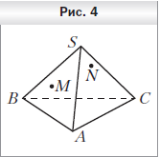
 ариант 2
ариант 2
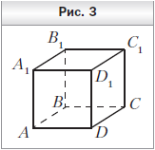
1. На рисунке 3 изображён куб ABCDA1B1C1D1. Укажите прямую пересечения плоскостей A1BC и ABB1.
2. Даны точки M, N и K такие, что MN = 23 см, MK = 14 см,
NK = 13 см. Сколько плоскостей можно провести через точки M, N и K? Ответ обоснуйте.
3 . Точки D и E — середины сторон AB и BC треугольника ABC соответственно. Плоскость α проходит через точки B, D и E. Докажите, что прямая AC лежит в плоскости α.
4. Точки M и N принадлежат соответственно граням SAB и SBC пирамиды SABC (рис. 4). Постройте точку пересечения прямой MN с плоскостью ABC.
5. Постройте сечение призмы ABCA1B1C1 плоскостью, проходящей через точки M, K и N, принадлежащие соответственно рёбрам AB, BC и CC1, причём прямые MK и AC не параллельны.
В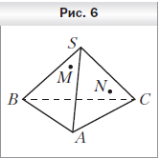
 ариант 3
ариант 3
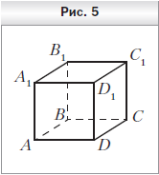
1. На рисунке 5 изображён куб ABCDA1B1C1D1. Укажите прямую пересечения плоскостей AD1C1 и B1BC .
2. Даны точки D, E и F такие, что DE = 11 см, EF = 16 см,
DF = 27 см. Сколько плоскостей можно провести через точки D, E и F? Ответ обоснуйте.
3. В окружности с центром O проведены диаметры AB и CD. Плоскость α проходит через точки A, C и O. Докажите, что прямая BD лежит в плоскости α.
4 . Точки M и N принадлежат соответственно граням SBC и SAC пирамиды SABC (рис. 6). Постройте точку пересечения прямой MN с плоскостью ABC.
5. Постройте сечение пирамиды SABC плоскостью, проходящей через точки M, K и N, принадлежащие соответственно рёбрам SA, SB и BC, причём прямые MK и AB не параллельны.
В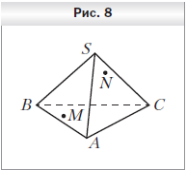 ариант 4
ариант 4
1 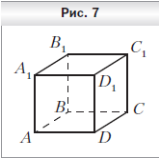 . На рисунке 7 изображён куб ABCDA1B1C1D1. Укажите прямую пересечения плоскостей D1BC и AA1B1.
. На рисунке 7 изображён куб ABCDA1B1C1D1. Укажите прямую пересечения плоскостей D1BC и AA1B1.
2. Даны точки B, C и D такие, что BC = 4 см, CD = 16 см, BD = 18 см. Сколько плоскостей можно провести через точки B, C и D? Ответ обоснуйте.
3 . Отрезок AD — биссектриса треугольника ABC, точка O — центр окружности, вписанной в треугольник ABC. Плоскость α проходит через точки A, O и C. Докажите, что точка B лежит в плоскости α.
4. Точки M и N принадлежат соответственно граням SAB и SBC пирамиды SABC (рис. 8). Постройте точку пересечения прямой MN с плоскостью SAC.
5. Постройте сечение куба ABCDA1B1C1D1 плоскостью, проходящей через вершину B1 и точки M и K, принадлежащие соответственно рёбрам AB и CC1.
Контрольная работа № 2 по теме «Параллельность в пространстве»
Вариант 1
1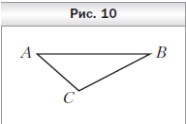
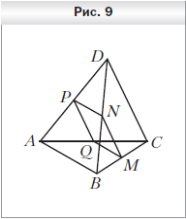 . Точки M, N, P и Q — середины отрезков BC, BD, AD и AC соответственно, AB = 14 см, CD = 18 см (рис. 9). Определите вид четырёхугольника MNPQ и вычислите его периметр.
. Точки M, N, P и Q — середины отрезков BC, BD, AD и AC соответственно, AB = 14 см, CD = 18 см (рис. 9). Определите вид четырёхугольника MNPQ и вычислите его периметр.
2. Плоскость α пересекает стороны AB и BC треугольника ABC в точках M и K соответственно и параллельна стороне AC, MK = 4 см, MB : MA = 2 : 3. Найдите сторону AC треугольника.
3 . Треугольник ABC является изображением правильного треугольника A1B1C1 (рис. 10). Постройте изображение высоты треугольника, опущенной на сторону A1C1.
4. Плоскости α и β параллельны. Из точки M, не принадлежащей этим плоскостям и не находящейся между ними, проведены два луча. Один из них пересекает плоскости α и β в точках A1 и B1, а другой — в точках A2 и B2 соответственно. Найдите отрезок B1B2 , если он на 2 см больше отрезка A1A2 , MB1 = 7 см, A1B1 = 4 см.
5. Точки A, B, C, не лежащие на одной прямой, являются параллельными проекциями трёх последовательных вершин правильного шестиугольника. Постройте изображение этого шестиугольника.
В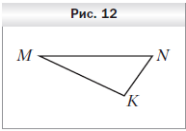 ариант 2
ариант 2
1 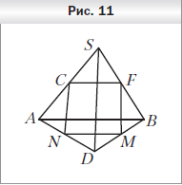 . Точки F, M, N и C — середины отрезков BS, DB, AD и AS соответственно, SD = 30 см, AB = 36 см (рис. 11). Определите вид четырёхугольника FMNC и вычислите его периметр.
. Точки F, M, N и C — середины отрезков BS, DB, AD и AS соответственно, SD = 30 см, AB = 36 см (рис. 11). Определите вид четырёхугольника FMNC и вычислите его периметр.
2. Плоскость β пересекает стороны AB и AC треугольника ABC в точках N и D соответственно и параллельна стороне BC, AD = 6 см, DN : CB = 3 : 4. Найдите сторону AC треугольника.
3 . Треугольник MNK является изображением правильного треугольника M1N1K1 (рис. 12). Постройте изображение биссектрисы треугольника, проведённой из вершины M1.
4. Плоскости α и β параллельны. Через точку M, находящуюся между этими плоскостями, проведены две прямые. Одна из них пересекает плоскости α и β в точках A1 и B1, а другая — в точках A2 и B2 соответственно. Найдите отрезок A1A2 , если он на 1 см меньше отрезка B1B2 , MA2 = 4 см, A2B2 = 10 см.
5. Точки A, B и O, не лежащие на одной прямой, являются соответственно параллельными проекциями двух вершин квадрата и его центра. Постройте изображение квадрата.
В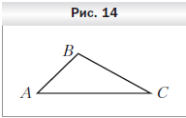 ариант 3
ариант 3
1 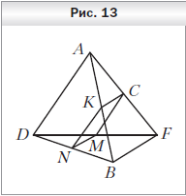 . Точки N, M, C и K — середины отрезков BD, DF, FA и AB соответственно, BF = 24 см, AD = 18 см (рис. 13). Определите вид четырёхугольника NMCK и вычислите его периметр.
. Точки N, M, C и K — середины отрезков BD, DF, FA и AB соответственно, BF = 24 см, AD = 18 см (рис. 13). Определите вид четырёхугольника NMCK и вычислите его периметр.
2. Плоскость α пересекает стороны MF и MK треугольника MFK в точках A и B соответственно и параллельна стороне FK,
AB = 12 см, AM : AF = 3 : 5. Найдите сторону FK треугольника.
3 . Треугольник ABC является изображением правильного треугольника A1B1C1 (рис. 14). Постройте изображение центра вписанной окружности треугольника A1B1C1.
4. Плоскости α и β параллельны. Из точки O, не принадлежащей этим плоскостям и не находящейся между ними, проведены два луча. Один из них пересекает плоскости α и β в точках C1 и D1, а другой — в точках C2 и D2 соответственно. Найдите отрезок C1C2, если он на 5 см меньше отрезка D1D2, OC1 = 4 см,
C1D1 = 10 см.
5. Точки A, B и O, не лежащие на одной прямой, являются соответственно параллельными проекциями двух вершин правильного треугольника и его центра. Постройте изображение этого треугольника.
В 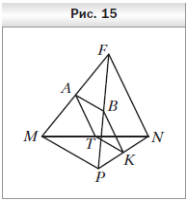 ариант 4
ариант 4
1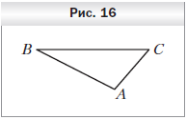 . Точки A, B, K и T — середины отрезков MF, PF, PN и MN соответственно, MP = 10 см, FN = 16 см (рис. 9). Определите вид четырёхугольника ABKT и вычислите его периметр.
. Точки A, B, K и T — середины отрезков MF, PF, PN и MN соответственно, MP = 10 см, FN = 16 см (рис. 9). Определите вид четырёхугольника ABKT и вычислите его периметр.
2 . Плоскость β пересекает стороны CF и CD треугольника CDF в точках M и N соответственно и параллельна стороне FD, MN = 6 см, FD = 21 см, MC = 10 см. Найдите сторону FC треугольника.
3. Треугольник ABC является изображением правильного треугольника A1B1C1 (рис. 16). Постройте изображение центра описанной окружности треугольника A1B1C1.
4. Плоскости α и β параллельны. Через точку D, находящуюся между этими плоскостями, проведены две прямые. Одна из них пересекает плоскости α и β в точках M1 и N1, а другая — в точках M2 и N2 соответственно. Найдите отрезок M1M2 , если он на 8 см больше отрезка N1N2 , N1M1= 30 см, DN1 = 5 см.
5. Точки A, B и M, не лежащие на одной прямой, являются соответственно параллельными проекциями двух соседних вершин параллелограмма и середины его противолежащей стороны. Постройте изображение этого параллелограмма.
Контрольная работа № 3 по теме «Перпендикулярность прямой и плоскости»
Вариант 1
1 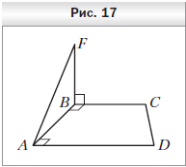 . На рисунке 17 изображена трапеция ABCD, у которой боковая сторона AB перпендикулярна основаниям AD и BC. Через вершину B проведена прямая BF, которая перпендикулярна прямой BC. Докажите, что прямая BC перпендикулярна плоскости ABF.
. На рисунке 17 изображена трапеция ABCD, у которой боковая сторона AB перпендикулярна основаниям AD и BC. Через вершину B проведена прямая BF, которая перпендикулярна прямой BC. Докажите, что прямая BC перпендикулярна плоскости ABF.
2. Через вершину A равностороннего треугольника ABC проведена прямая DA, перпендикулярная плоскости треугольника. Вычислите расстояние от точки D до прямой BC, если AD = 3 см, AB = 6 см.
3. Точка D находится на расстоянии 4 см от каждой вершины правильного треугольника ABC, сторона которого равна 6 см. Найдите расстояние от точки D до плоскости ABC.
4. Через вершину D прямоугольника ABCD к его плоскости проведён перпендикуляр DE. Точка E удалена от стороны AB на 10 см, а от стороны BC — на 17 см. Найдите диагональ прямоугольника, если DE = 8 см.
5. Основание и боковая сторона равнобедренного треугольника равны 30 см и 17 см соответственно. Некоторая точка пространства находится на расстоянии 2![]() см от каждой стороны треугольника. Найдите расстояние от данной точки до плоскости треугольника.
см от каждой стороны треугольника. Найдите расстояние от данной точки до плоскости треугольника.
Вариант 2
1 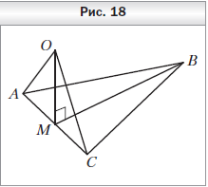 . На рисунке 18 изображён равнобедренный треугольник ABC (AB = BC), точка M — середина стороны AC. Через точку M проведена прямая MO, перпендикулярная прямой BM. Докажите, что прямая BM перпендикулярна плоскости AOC.
. На рисунке 18 изображён равнобедренный треугольник ABC (AB = BC), точка M — середина стороны AC. Через точку M проведена прямая MO, перпендикулярная прямой BM. Докажите, что прямая BM перпендикулярна плоскости AOC.
2. Через вершину C квадрата ABCD проведена прямая MC, перпендикулярная плоскости квадрата. Вычислите расстояние от точки M до прямой BD, если MC = 1 см, CD = 4 см.
3. Точка K находится на расстоянии 4 см от каждой вершины правильного треугольника ABC. Найдите сторону треугольника, если точка K удалена от плоскости ABC на 2 см.
4. Через вершину A прямоугольника ABCD к его плоскости проведён перпендикуляр AP. Найдите расстояние от точки P до прямой CD, если BC = 12 см, BD = 13 см, а точка P удалена от прямой BC на ![]() см.
см.
5. Высота и основание равнобедренного треугольника равны 8 см и 12 см соответственно. Некоторая точка пространства находится на расстоянии 4 см от плоскости треугольника и равноудалена от его сторон. Найдите расстояние от этой точки до сторон треугольника.
Вариант 3
1 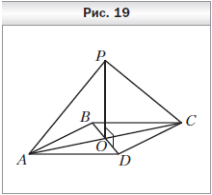 . На рисунке 19 изображён квадрат ABCD. Через точку O пересечения диагоналей проведена прямая OP, перпендикулярная прямой BD. Докажите, что прямая BD перпендикулярна плоскости APC.
. На рисунке 19 изображён квадрат ABCD. Через точку O пересечения диагоналей проведена прямая OP, перпендикулярная прямой BD. Докажите, что прямая BD перпендикулярна плоскости APC.
2. Через вершину B равнобедренного треугольника ABC проведена прямая KB, перпендикулярная плоскости треугольника, AB = BC = 10 см, AC = 12 см. Найдите расстояние от точки K до прямой AC, если KB = 4 см.
3. Точка M находится на расстоянии 8 см от каждой вершины квадрата ABCD. Найдите сторону квадрата, если точка M удалена от его плоскости на 4![]() см.
см.
4. Через вершину B прямоугольника ABCD к его плоскости проведён перпендикуляр MB. Точка M удалена от стороны AD на 25 см, а от стороны CD — на 10![]() см. Найдите диагональ прямоугольника, если AB = 15 см.
см. Найдите диагональ прямоугольника, если AB = 15 см.
5. Основание и боковая сторона равнобедренного треугольника равны 12 см и 10 см соответственно. Некоторая точка пространства находится на расстоянии 5 см от каждой стороны треугольника. Найдите расстояние от данной точки до плоскости треугольника.
Вариант 4
1 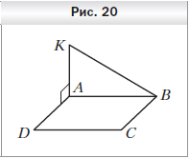 . На рисунке 20 изображён прямоугольник ABCD. Через вершину A проведена прямая AK, которая перпендикулярна прямой AD. Докажите, что прямая AD перпендикулярна плоскости AKB.
. На рисунке 20 изображён прямоугольник ABCD. Через вершину A проведена прямая AK, которая перпендикулярна прямой AD. Докажите, что прямая AD перпендикулярна плоскости AKB.
2. Через вершину B ромба ABCD проведена прямая BM, перпендикулярная плоскости ромба. Найдите расстояние от точки M до прямой AC, если MB = 12 см, DC = 16 см, AC = 20 см.
3. Точка F находится на расстоянии 5![]() см от каждой вершины квадрата ABCD, сторона которого равна 10 см. Найдите расстояние от точки F до плоскости квадрата.
см от каждой вершины квадрата ABCD, сторона которого равна 10 см. Найдите расстояние от точки F до плоскости квадрата.
4. Через вершину A прямоугольника ABCD к его плоскости проведён перпендикуляр AK. Точка K удалена от стороны BC на 15 см. Найдите расстояние от точки K до стороны CD, если BD = ![]() см, AK = 12 см.
см, AK = 12 см.
5. Стороны треугольника равны 13 см, 14 см и 15 см. Некоторая точка пространства находится на расстоянии 5 см от каждой стороны треугольника. Найдите расстояние от данной точки до плоскости треугольника.
Контрольная работа № 4 по теме «Угол между прямой и плоскостью. Угол между плоскостями. Перпендикулярные плоскости»
Вариант 1
1. Из точки D, которая лежит вне плоскости α, проведены к этой плоскости наклонные DK и DB, образующие с ней углы 45° и 60° соответственно. Найдите длину проекции наклонной DK на плоскость α, если DB = 10![]() см.
см.
2. Точка A принадлежит одной из граней двугранного угла и удалена от другой грани на 8 см. Найдите расстояние от точки A до ребра двугранного угла, если величина этого угла равна 45°.
3. Угол между плоскостями треугольников ABC и ABD равен 45°. Треугольник ABC — равносторонний со стороной 4![]() см, треугольник ABD — равнобедренный,
см, треугольник ABD — равнобедренный,
AD = BD = ![]() см. Найдите отрезок CD.
см. Найдите отрезок CD.
4. Концы отрезка, длина которого равна 5![]() см, принадлежат двум перпендикулярным плоскостям. Расстояния от концов этого отрезка до линии пересечения плоскостей равны 5 см и 8 см. Найдите расстояние между основаниями перпендикуляров, опущенных из концов отрезка на линию пересечения плоскостей.
см, принадлежат двум перпендикулярным плоскостям. Расстояния от концов этого отрезка до линии пересечения плоскостей равны 5 см и 8 см. Найдите расстояние между основаниями перпендикуляров, опущенных из концов отрезка на линию пересечения плоскостей.
5. Через гипотенузу прямоугольного равнобедренного треугольника проведена плоскость, которая образует с плоскостью треугольника угол 45°. Найдите синусы углов, которые образуют катеты треугольника с этой плоскостью.
Вариант 2
1. Из точки K, которая лежит вне плоскости α, проведены к этой плоскости наклонные KA и KB, образующие с ней углы 45° и 30° соответственно. Найдите длину проекции наклонной KB на плоскость α, если KA = 8![]() см.
см.
2. Точка M принадлежит одной из граней двугранного угла и удалена от его ребра на 12 см. Найдите расстояние от точки M до другой грани угла, если величина этого угла равна 60°.
3. Угол между плоскостями треугольников ABC и AKC равен 60°, AC = 24 см,
BC = BA = 20 см, KC = KA = 15 см. Найдите отрезок BK.
4. Концы отрезка, длина которого равна 16 см, принадлежат двум перпендикулярным плоскостям. Расстояния от концов этого отрезка до линии пересечения плоскостей равны 8 см и 8![]() см. Найдите углы, которые образует отрезок с данными плоскостями.
см. Найдите углы, которые образует отрезок с данными плоскостями.
5. Через сторону правильного треугольника проведена плоскость, которая образует с плоскостью треугольника угол 30°. Найдите синусы углов, которые образуют две другие стороны треугольника с этой плоскостью.
Вариант 3
1. Из точки A, которая лежит вне плоскости α, проведены к этой плоскости наклонные AC и AD, образующие с ней углы 45° и 60° соответственно. Найдите длину проекции наклонной AD на плоскость α, если AC = 4![]() см.
см.
2. Точка A принадлежит одной из граней двугранного угла и удалена от другой грани на 6 см. Найдите расстояние от точки A до ребра двугранного угла, если величина этого угла равна 30°.
3. Угол между плоскостями треугольников ABC и ABD равен 60°, AC = BC = 20 см, AB = 24 см, AD = BD, ∠ADB = 90°. Найдите отрезок CD.
4. Концы отрезка, длина которого равна 10 см, принадлежат двум перпендикулярным плоскостям. Углы, которые образует отрезок с данными плоскостями, равны 45° и 60°. Найдите расстояние между основаниями перпендикуляров, опущенных из концов отрезка на линию пересечения плоскостей.
5. Через катет прямоугольного равнобедренного треугольника проведена плоскость, которая образует с плоскостью треугольника угол 60°. Найдите синус угла, который образует гипотенуза треугольника с этой плоскостью.
Вариант 4
1. Из точки M, которая лежит вне плоскости α, проведены к этой плоскости наклонные MN и MK, образующие с ней углы 30° и 45° соответственно. Найдите длину наклонной MK, если длина проекции наклонной MN на плоскость α равна 4![]() см.
см.
2. Точка M принадлежит одной из граней двугранного угла и удалена от его ребра на 4 см. Найдите расстояние от точки M до другой грани угла, если величина этого угла равна 45°.
3. Угол между плоскостями ABC и ADC равен 60°, AB = BC = AC = 12 см, AD = CD, ∠ADC = 120°. Найдите отрезок BD.
4. Концы отрезка, длина которого равна 14 см, принадлежат двум перпендикулярным плоскостям, а расстояния от его концов до линии пересечения плоскостей равны 8 см и 5 см. Найдите расстояние между основаниями перпендикуляров, опущенных из концов отрезка на линию пересечения плоскостей.
5. Через сторону правильного треугольника проведена плоскость, которая образует с двумя остальными сторонами треугольника углы по 30°. Найдите синус угла между плоскостью данного треугольника и проведённой плоскостью.
Итоговая контрольная работа по геометрии 10 класс
Вариант 1
1. Точка M равноудалена от всех сторон квадрата со стороной 6 см и находится на расстоянии 9 см от плоскости квадрата. Найдите расстояние от точки M до сторон квадрата.
2. Точка A находится на расстоянии 9 см от плоскости α. Наклонные AB и AC образуют с плоскостью α углы 45° и 60° соответственно. Найдите расстояние между точками B и C , если угол между проекциями наклонных равен 150°.
3. Через вершину B треугольника ABC, в котором AB = BC = 34 см, AC = 32 см, проведён перпендикуляр DB к плоскости треугольника. Найдите угол между плоскостями ABC и ADC, если DB = 20 см.
4. Основание пирамиды MABCD — квадрат со стороной 6 см, боковые грани ABM и CBM перпендикулярны плоскости основания пирамиды, AM = 10 см. Найдите площадь боковой поверхности пирамиды.
5. Основанием прямого параллелепипеда является ромб со стороной a и острым углом α. Бóльшая диагональ параллелепипеда наклонена к плоскости основания под углом β. Найдите площадь боковой поверхности параллелепипеда.
Вариант 2
1. Точка F равноудалена от всех вершин прямоугольника со сторонами 12 см и 16 см и находится на расстоянии 5 см от плоскости прямоугольника. Найдите расстояние от точки F до вершин прямоугольника.
2. Точка K находится на расстоянии 4 см от плоскости α. Наклонные KA и KB образуют с плоскостью α углы 45° и 30° соответственно, а угол между наклонными равен 135°. Найдите расстояние между точками A и B.
3. Через вершину C треугольника ABC, в котором AC = BC, AC = 32 см, проведён перпендикуляр KC к плоскости треугольника. Найдите угол между плоскостями ABC и ABK, если AB = 12 см, AK = 10 см, KC = 2 см.
4. Основание пирамиды MABCD — квадрат, боковые грани ADM и CDM перпендикулярны плоскости основания пирамиды, MB = 3![]() см, MA = 15 см. Найдите площадь боковой поверхности пирамиды.
см, MA = 15 см. Найдите площадь боковой поверхности пирамиды.
5. Основанием прямого параллелепипеда является ромб со стороной a и острым углом α. Меньшая диагональ параллелепипеда наклонена к плоскости основания под углом β. Найдите площадь боковой поверхности параллелепипеда.
Вариант 3
1. Точка A равноудалена от всех сторон правильного треугольника со стороной 30 см и находится на расстоянии 5 см от плоскости треугольника. Найдите расстояние от точки A до сторон треугольника.
2. Точка B находится на расстоянии 3![]() см от плоскости α. Наклонные BA и BC образуют с этой плоскостью углы 60° и 30° соответственно. Найдите расстояние между точками A и C, если угол между проекциями наклонных равен 120°.
см от плоскости α. Наклонные BA и BC образуют с этой плоскостью углы 60° и 30° соответственно. Найдите расстояние между точками A и C, если угол между проекциями наклонных равен 120°.
3. Через вершину A треугольника ABC, в котором AB = AC = 13 см, BC = 10 см, проведён перпендикуляр NA к плоскости треугольника. Найдите угол между плоскостями ABC и NBC, если NB = 15 см.
4. Основание пирамиды MABCD — квадрат, боковые грани BCM и DCM перпендикулярны плоскости основания пирамиды, MB = 13 см, MC = 12 см. Найдите площадь боковой поверхности пирамиды.
5. Основанием прямого параллелепипеда является ромб со стороной a и тупым углом α. Меньшая диагональ параллелепипеда наклонена к плоскости основания под углом β. Найдите площадь боковой поверхности параллелепипеда.
Вариант 4
1. Точка D равноудалена от всех вершин правильного треугольника со стороной 12 см и находится на расстоянии 4 см от плоскости треугольника. Найдите расстояние от точки D до вершин треугольника.
2. Точка C находится на расстоянии 6 см от плоскости α. Наклонные CA и CB образуют с плоскостью α углы 30° и 45° соответственно. Найдите расстояние между точками A и B, если угол между проекциями наклонных равен 30°.
3. Через вершину D правильного треугольника ADB, в котором AD = 8 см, проведен перпендикуляр PD к плоскости треугольника. Найдите угол между плоскостями ADB и APB, если PB = 10 см.
4. Основание пирамиды MABCD — квадрат, боковые грани MAB и MAD перпендикулярны плоскости основания пирамиды, AD = 8 см, MA = 15 см. Найдите площадь боковой поверхности пирамиды.
5. Основанием прямого параллелепипеда является ромб со стороной a и тупым углом α. Бóльшая диагональ параллелепипеда наклонена к плоскости основания под углом β. Найдите площадь боковой поверхности параллелепипеда.
КИМ 11 КЛАСС
Контрольная работа № 1 по теме «Показательная функция. Показательные уравнения и неравенства»
Вариант 1
1. Сравните числа m и n, если:
1) ![]() 2)
2) ![]()
2. Решите уравнение:
1) ![]() ; 2)
; 2) ![]() .
.
3. Найдите множество решений неравенства ![]() .
.
4. Решите уравнение:
1) ![]() 2)
2) ![]() .
.
5. Решите неравенство:
1) ![]() 2)
2) ![]() .
.
Вариант 2
1. Сравните числа a и b, если:
1) ![]() 2)
2) ![]()
2. Решите уравнение:
1) ![]() ; 2)
; 2) ![]() .
.
3. Найдите множество решений неравенства ![]() .
.
4. Решите уравнение:
1) ![]() 2)
2) ![]() .
.
5. Решите неравенство:
1) ![]() 2)
2) ![]() .
.
Вариант 3
1. Сравните числа m и n, если:
1) ![]() 2)
2) ![]()
2. Решите уравнение:
1) ![]() ; 2)
; 2) ![]() .
.
3. Найдите множество решений неравенства ![]() .
.
4. Решите уравнение:
1) ![]() 2)
2) ![]() .
.
5. Решите неравенство:
1) 2) .
Вариант 4
1. Сравните числа a и b, если:
1) 2)
2. Решите уравнение:
1) ; 2) .
3. Найдите множество решений неравенства .
4. Решите уравнение:
1) 2) .
5. Решите неравенство:
1) 2) .
Контрольная работа № 2 по теме «Интеграл и его применение»
Вариант 1
1. Вычислите интеграл:

2. Найдите площадь фигуры, ограниченной параболой ![]() и прямыми y = 0 и x = 3.
и прямыми y = 0 и x = 3.
3. Найдите первообразную функции ![]() график которой проходит через точку A (1; 6).
график которой проходит через точку A (1; 6).
4 ![]() . Вычислите интеграл:
. Вычислите интеграл:
5. Найдите площадь фигуры, ограниченной графиками функций ![]() и y = x + 4.
и y = x + 4.
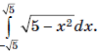
6 . Используя геометрический смысл интеграла, вычислите
Вариант 2
1. Вычислите интеграл:

2. Найдите площадь фигуры, ограниченной параболой ![]() и прямыми y = 0 и x = 2.
и прямыми y = 0 и x = 2.
3. Найдите первообразную функции ![]() график которой проходит через точку M (1; −3).
график которой проходит через точку M (1; −3).
4. Вычислите интеграл:
![]()
5 . Найдите площадь фигуры, ограниченной графиками функций ![]() и y = 3 – x .
и y = 3 – x .
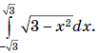
6. Используя геометрический смысл интеграла, вычислите
Контрольная работа № 3 по теме «Элементы комбинаторики. Бином Ньютона»
Вариант 1
1. Найдите значение выражения:
1) ![]() 2)
2) ![]()
2. В распоряжении командира воинского подразделения есть пять солдат. Сколько у него существует способов направить этих солдат для охраны пяти объектов?
3. Сколько существует чётных трёхзначных чисел, в записи которых используются только цифры 1, 2, 3, 5 (все цифры в записи числа должны быть различны)?
4. Докажите, что при всех n ∈ N выполняется неравенство ![]() .
.
5. Выражение ![]() разложили по формуле бинома Ньютона. Какой член разложения не зависит от x?
разложили по формуле бинома Ньютона. Какой член разложения не зависит от x?
6. Сколько существует способов выбрать из натуральных чисел от 1 до 29 включительно шесть чисел так, чтобы среди выбранных было ровно два чётных числа?
Вариант 2
1. Найдите значение выражения:
1) ![]() 2)
2) ![]()
2. Семья из четырёх человек приобрела 4 билета в театр. Сколько существует способов рассадить членов этой семьи на места в соответствии с купленными билетами?
3. Сколько существует чётных трёхзначных чисел, в записи которых используются только цифры 1, 3, 4, 7 (все цифры в записи числа должны быть различны)?
4. Докажите, что при всех n ∈ N выполняется неравенство ![]() .
.
5. Выражение ![]() разложили по формуле бинома Ньютона. Какой член разложения не зависит от x?
разложили по формуле бинома Ньютона. Какой член разложения не зависит от x?
6. Сколько существует способов выбрать из натуральных чисел от 1 до 25 включительно семь чисел так, чтобы среди выбранных было ровно два чётных числа?
Контрольная работа № 4 по теме «Элементы теории вероятностей»
Вариант 1
1. О событиях A и B некоторого испытания известно, что P (A) = 30%, P (B) = 50% и P (A ∪ B) = 80%. Найдите P (A ∩ B).
2. Найдите значение P (x = 5) и математическое ожидание случайной величины x.
| Значение x | 2 | 3 | 5 | 10 |
| Вероятность, % | 5 | 40 |
| 15 |
3. Имеются два принтера, которые обслуживаются независимо один от другого. Вероятность того, что в определённый день в первом принтере закончится тонер, равна 3%, а во втором принтере — 1%. Найдите вероятность того, что в этот день можно будет пользоваться обоими принтерами.
4. Вероятность того, что лотерейный билет выигрышный, равна 0,5%. Чему равна вероятность того, что из 8 купленных наугад лотерейных билетов 3 окажутся выигрышными?
5. В некоторой местности вероятность того, что наугад выбранный человек курит, равна 20%, а вероятность того, что наугад выбранный человек имеет сердечно-сосудистые заболевания, равна 30%. Известно, что среди людей, имеющих сердечно-сосудистые заболевания, в этой местности 60% курят. Найдите вероятность того, что наугад выбранный курильщик имеет сердечно-сосудистые заболевания.
Вариант 2
1. О событиях A и B некоторого испытания известно, что P (A) = 0,4, P (A ∪ B) = 0,9 и P (A ∩B) = 0,3. Найдите P (B).
2. Найдите значение P (z = 0) и математическое ожидание случайной величины z.
| Значение z | −2 | 0 | 1 | 4 |
| Вероятность, % | 30 |
| 20 | 40 |
3. В математических олимпиадах обычно участвует больше мальчиков, а в олимпиадах по иностранному языку — девочек. Вероятность того, что кто-то из мальчиков победит на олимпиаде по математике, равна 0,7, а на олимпиаде по иностранному языку — 0,35. Найдите вероятность того, что на обеих олимпиадах победу одержат девочки.
4. Вероятность того, что посетитель магазина совершит покупку, равна 40%. Какова вероятность того, что из 12 случайных посетителей магазина 8 совершат покупку?
5. Известно, что 80% выпускаемых мобильных телефонов имеют доступ к сети Интернет, а 70% — имеют сенсорный экран. Вероятность того, что наугад выбранный телефон с сенсорным экраном будет иметь доступ к сети Интернет, равна 96%. Найдите вероятность того, что наугад выбранный телефон с доступом в Интернет будет иметь сенсорный экран.
Вариант 3
1. О несовместных событиях A и B некоторого испытания известно, что P (A) = 20% и P (A ∪ B) = 75%. Найдите P (B).
2. Найдите значение P (y = 4) и математическое ожидание случайной величины y.
| Значение y | 2 | 3 | 4 | 8 |
| Вероятность, % | 10 | 70 |
| 20 |
3. В соревнованиях по стрельбе из лука участвуют два спортсмена. Первый спортсмен поражает мишень с вероятностью 92%, а второй спортсмен — с вероятностью 96%. Найдите вероятность того, что ни один из этих спортсменов не поразит мишень.
4. Вероятность того, что перепад напряжения приведёт к поломке электроприбора, равна 0,08. Какова вероятность, что из 5 разных случаев перепадов напряжения 2 приведут к необходимости ремонтировать прибор?
5. В автомате, предлагающем различные напитки, 45% продаж приходится на кофе, а в 60% случаев покупатель приобретает напиток с сахаром. Известно, что в 80% случаев покупки кофе в него добавляют сахар. Найдите вероятность того, что покупатель, предпочитающий сладкий напиток, купит кофе.
Итоговая контрольная работа по теме «Обобщение и систематизация знаний учащихся»
Вариант 1
1. Решите уравнение:
1) ![]() ; 3)
; 3) ![]()
2) ![]()
2. Решите неравенство:
1) ![]() 2)
2) ![]()
3. Найдите промежутки возрастания и убывания и точки экстремума функции ![]() .
.
4. Вычислите интеграл ![]()
5. В двух коробках хранятся шары. В первой коробке лежат 8 шаров, из которых 2 белых и 6 чёрных, во второй — 6 шаров, из которых 5 белых и 1 чёрный. Из каждой коробки наугад вынули по одному шару. Какова вероятность того, что оба вынутых шара окажутся чёрными?
6. При каких значениях b и c парабола ![]() касается прямой
касается прямой ![]() в точке A (−1; 8)?
в точке A (−1; 8)?
Вариант 2
1. Решите уравнение:
1) ![]() ; 3)
; 3) ![]()
2) ![]()
2. Решите неравенство:
1) ![]() 2)
2) ![]()
3. Найдите промежутки возрастания и убывания и точки экстремума функции ![]()
4. Вычислите интеграл ![]()
5. Стрелок делает два независимых выстрела — сначала в первую мишень, потом во вторую. Вероятность того, что стрелок попадёт в первую мишень, составляет 70%, во вторую — 90%. Какова вероятность того, что стрелок попадёт только во вторую мишень?
6. При каких значениях b и c парабола ![]() касается прямой
касается прямой
![]() в точке B (−2; 29)?
в точке B (−2; 29)?
Вариант 3
1. Решите уравнение:
1) ![]() ; 3)
; 3) ![]()
2) ![]()
2. Решите неравенство:
1) ![]() 2)
2) ![]()
3. Найдите промежутки возрастания и убывания и точки экстремума функции ![]()
4. Вычислите интеграл ![]()
5. Игральный кубик последовательно бросают два раза. Какова вероятность того, что только во второй раз на кубике выпадет количество очков, кратное трём?
6. При каких значениях b и c парабола касается прямой в точке C (3; 13)?
Контрольная работа № 1 по теме «Координаты и векторы в пространстве»
Вариант 1
1. Точка A — середина отрезка MK. Найдите координаты точки A и длину отрезка MK, если M (5; −2; 1), K (3; 4; −3).
2. Точки A и B симметричны относительно точки C. Найдите координаты точки B, если A (−3; 5; −7), C (6; 2; −1).
3. Даны векторы ![]() (3; −2; −1) и
(3; −2; −1) и ![]() (1; 2; 4). Найдите:
(1; 2; 4). Найдите:
1) координаты вектора ![]() ;
;
2) косинус угла между векторами ![]() и
и ![]() .
.
4. Даны векторы ![]() (2; −6; 8) и
(2; −6; 8) и ![]() (−1; k; −4). При каком значении k векторы
(−1; k; −4). При каком значении k векторы ![]() и
и ![]() :
:
1) коллинеарны;
2) перпендикулярны?
5. Составьте уравнение плоскости, проходящей через точку A и перпендикулярной прямой AB, если A (1; 2; −3), B (4; 8; −6).
6. Дан куб ABCDA1B1C1D1, ребро которого равно 1 см. На диагонали C1D его грани отметили точку M так, что DM : MC1 = 5 : 3.
1) Выразите вектор ![]() через векторы
через векторы ![]() ,
, ![]() и
и ![]() .
.
2) Найдите модуль вектора ![]() .
.
Вариант 2
1. Точка M — середина отрезка AB. Найдите координаты точки M и длину отрезка AB, если A (6; −5; 2), B (−4; 3; 10).
2. Точки M и K симметричны относительно точки D. Найдите координаты точки K, если M (4; −6; 3), D (−2; 1; 5).
3. Даны векторы ![]() (2; −1; 3) и
(2; −1; 3) и ![]() (−1; 2; 5). Найдите:
(−1; 2; 5). Найдите:
1) координаты вектора ![]() ;
;
2) косинус угла между векторами ![]() и
и ![]() .
.
4. Даны векторы ![]() (5; −4; 6) и
(5; −4; 6) и ![]() (15; −12; p). При каком значении p векторы
(15; −12; p). При каком значении p векторы ![]() и
и ![]() :
:
1) коллинеарны;
2) перпендикулярны?
5. Составьте уравнение плоскости, проходящей через точку B и перпендикулярной прямой BC, если B (3; −2; 4), C (−2; 8; 19).
6. Дан куб ABCDA1B1C1D1, ребро которого равно 1 см. На диагонали AD1 его грани отметили точку E так, что AE : ED1 = 2 : 7.
1) Выразите вектор ![]() через векторы
через векторы ![]() , и .
, и .
2) Найдите модуль вектора ![]() .
.
Контрольная работа № 2 по теме «Цилиндр. Конус. Усечённый конус. Комбинации цилиндра, конуса и усечённого конуса с многогранниками»
Вариант 1
1. Радиус основания цилиндра равен 6 см, а высота – 5 см. Найдите диагональ осевого сечения цилиндра.
2. Найдите высоту конуса, диаметр основания которого равен 10 см, а образующая наклонена к плоскости основания под углом 30°.
3. Радиусы оснований усечённого конуса равны 9 см и 17 см, а высота – 15 см. Найдите образующую усечённого конуса.
4. В цилиндре параллельно его оси проведено сечение, диагональ которого образует с плоскостью основания угол ![]() . Это сечение пересекает основание по хорде, стягивающей дугу, градусная мера которой равна α, 0° R.
. Это сечение пересекает основание по хорде, стягивающей дугу, градусная мера которой равна α, 0° R.
5. Сторона основания правильной четырёхугольной призмы равна 8 см, а диагональ боковой грани образует с плоскостью основания угол 60°. Найдите площадь боковой поверхности цилиндра, вписанного в данную призму.
6. Основание пирамиды – треугольник, одна из сторон которого равна c, а противолежащий ей угол равен γ. Все боковые рёбра пирамиды наклонены к плоскости основания под углом α. Найдите площадь боковой поверхности конуса, описанного около данной пирамиды.
Вариант 2
1. Диагональ осевого сечения цилиндра равна 10 см, а высота цилиндра – 8 см. Найдите радиус основания цилиндра.
2. Найдите диаметр основания конуса, высота которого равна 12 см, а образующая наклонена к плоскости основания под углом 60°.
3. Радиусы оснований усечённого конуса равны 14 см и 10 см, а образующая –
5 см. Найдите высоту усечённого конуса.
4. В цилиндре параллельно его оси проведено сечение, которое пересекает основание по хорде, стягивающей дугу, градусная мера которой равна α,
0° d и образует с плоскостью основания угол β.
5. Сторона основания правильной треугольной призмы равна 18 см, а диагональ боковой грани образует с плоскостью основания угол 45°. Найдите площадь боковой поверхности цилиндра, вписанного в данную призму.
6. Основание пирамиды — прямоугольный треугольник, катет которого равен b, а противолежащий острый угол равен β. Все боковые рёбра пирамиды наклонены к плоскости основания под углом α. Найдите площадь боковой поверхности конуса, описанного около данной пирамиды.
Вариант 3
1. Радиус основания цилиндра равен 6 см, а диагональ осевого сечения – 13 см. Найдите высоту цилиндра.
2. Найдите образующую конуса, если она наклонена к плоскости основания под углом 45°, а высота конуса равна 18 см.
3. Радиус меньшего основания усечённого конуса равен 8 см, образующая – 15 см, а высота – 9 см. Найдите радиус большего основания усечённого конуса.
4. Радиус основания цилиндра равен R. Параллельно оси цилиндра проведено сечение. Хорда нижнего основания, принадлежащая сечению, видна из центра этого основания под углом 2α. Отрезок, соединяющей центр верхнего основания цилиндра с точкой окружности нижнего основания, образует с плоскостью основания угол β. Найдите площадь сечения.
5. Высота правильной четырёхугольной призмы равна 6 см, а диагональ боковой грани образует с плоскостью основания угол 60°. Найдите площадь боковой поверхности цилиндра, вписанного в данную призму.
6. Основание пирамиды – прямоугольник, одна из сторон которого равна a и образует с диагональю прямоугольника угол α. Все боковые рёбра пирамиды наклонены к плоскости основания под углом β. Найдите площадь боковой поверхности конуса, описанного около данной пирамиды.
Вариант 4
1. Радиус основания цилиндра равен 5 см, а высота – 2![]() см. Найдите диагональ осевого сечения цилиндра.
см. Найдите диагональ осевого сечения цилиндра.
2. Найдите радиус основания конуса, образующая которого равна 14 см и наклонена к плоскости основания под углом 60°.
3. Радиус большего основания усечённого конуса равен 11 см, образующая – 13 см, а высота – 12 см. Найдите радиус меньшего основания усечённого конуса.
4. В цилиндре параллельно его оси проведено сечение. Диагональ сечения наклонена к плоскости основания под углом β. Хорда нижнего основания, принадлежащая сечению, видна из центра этого основания под углом α и удалена от него на расстояние, равное d. Найдите площадь сечения.
5. Высота правильной треугольной призмы равна 12 см, а диагональ боковой грани образует с плоскостью основания угол 30°. Найдите площадь боковой поверхности цилиндра, вписанного в данную призму.
6. Основание пирамиды – равнобедренный треугольник с боковой стороной a и углом β при вершине. Все боковые рёбра пирамиды наклонены к плоскости основания под углом ![]() . Найдите площадь боковой поверхности конуса, описанного около данной пирамиды.
. Найдите площадь боковой поверхности конуса, описанного около данной пирамиды.
Контрольная работа № 3 по теме «Сфера и шар. Уравнение сферы. Комбинации шара с многогранниками, цилиндром и конусом»
Вариант 1
1. Диаметр шара равен 26 см. Найдите площадь сечения шара плоскостью, удалённой от его центра на 12 см.
2. Составьте уравнение сферы с центром в точке A (6; −2; 7), проходящей через точку B (8; −1; 5).
3. Угол при вершине осевого сечения конуса равен 120°. Вокруг конуса описан шар, радиус которого равен 8 см. Найдите площадь боковой поверхности конуса.
4. Определите, является ли уравнение x2 + y2 + z2 − 6x + 10y + 2z + 31 = 0 уравнением сферы. В случае утвердительного ответа укажите координаты центра сферы и её радиус.
5. Высота правильной треугольной пирамиды равна h, а двугранный угол пирамиды при ребре основания равен α. Найдите радиус шара, вписанного в эту пирамиду.
Вариант 2
1. Диаметр шара равен 10 см. Найдите расстояние от центра шара до его сечения, площадь которого равна 9π см2.
2. Составьте уравнение сферы с центром в точке C (−3; 1; 9), проходящей через точку D (1; 5; 8).
3. Осевым сечением конуса является равносторонний треугольник. Вокруг конуса описан шар, радиус которого равен 6 см. Найдите площадь боковой поверхности конуса.
4. Определите, является ли уравнение x2 + y2 + z2 + 12x − 4y − 18z + 112 = 0 уравнением сферы. В случае утвердительного ответа укажите координаты центра сферы и её радиус.
5. Высота правильной четырёхугольной пирамиды равна h, а двугранный угол пирамиды при ребре основания равен ![]() . Найдите радиус шара, вписанного в эту пирамиду.
. Найдите радиус шара, вписанного в эту пирамиду.
Вариант 3
1. Площадь сечения шара равна 64π см2. Это сечение удалено от центра шара на 6 см. Найдите радиус шара.
2. Составьте уравнение сферы с центром в точке M (2; 4; −10), проходящей через точку K (3; −2; −13).
3. Осевым сечением конуса является равнобедренный прямоугольный треугольник. Вокруг конуса описан шар, радиус которого равен 4 см. Найдите площадь боковой поверхности конуса.
4. Определите, является ли уравнение x2 + y2 + z2 − 8x − 14y − 16z + 120 = 0 уравнением сферы. В случае утвердительного ответа укажите координаты центра сферы и её радиус.
5. Апофема правильной треугольной пирамиды равна b, а двугранный угол пирамиды при ребре основания равен α. Найдите радиус шара, вписанного в эту пирамиду.
Вариант 4
1. Диаметр шара равен 34 см. Найдите площадь сечения шара плоскостью, удалённой от его центра на 15 см.
2. Составьте уравнение сферы с центром в точке E (−1; −5; 6), проходящей через точку F (2; −7; 4).
3. Угол при вершине осевого сечения конуса равен 120°. Вокруг конуса описан шар, радиус которого равен 2 см. Найдите площадь боковой поверхности конуса.
4. Определите, является ли уравнение x2 + y2 + z2 − 2x + 6y − 20z + 94 = 0 уравнением сферы. В случае утвердительного ответа укажите координаты центра сферы и её радиус.
5. Апофема правильной четырёхугольной пирамиды равна b, а двугранный угол пирамиды при ребре основания равен β. Найдите радиус шара, вписанного в эту пирамиду.
Контрольная работа № 4 по теме «Объёмы многогранников»
Вариант 1
1. Основание прямой треугольной призмы – прямоугольный треугольник с катетами 3 см и 10 см. Высота призмы равна 8 см. Найдите объём призмы.
2. Найдите объём правильной четырёхугольной пирамиды, боковое ребро которой равно 12 см и образует с плоскостью основания угол 45°.
3. Найдите объём правильной усечённой треугольной пирамиды, стороны оснований которой равны 6 см и 8 см, а высота – 9 см.
4. Основанием пирамиды является равнобедренный треугольник с углом α при основании и радиусом вписанной окружности r. Две боковые грани пирамиды, содержащие боковые стороны основания, перпендикулярны плоскости основания, а третья наклонена к ней под углом β. Найдите объём пирамиды.
5. В правильной треугольной пирамиде плоский угол при вершине равен α. Найдите объём пирамиды, если её высота равна h.
Вариант 2
1. Основание прямой четырёхугольной призмы – параллелограмм со сторонами 4 см и 5![]() см и углом 45° между ними. Высота призмы равна 6 см. Найдите объём призмы.
см и углом 45° между ними. Высота призмы равна 6 см. Найдите объём призмы.
2. Найдите объём правильной четырёхугольной пирамиды, боковое ребро которой образует с плоскостью основания угол 60°, а сторона основания равна 8 см.
3. Найдите объём правильной усечённой четырёхугольной пирамиды, стороны оснований которой равны 4 см и 7 см, а высота – 12 см.
4. Основанием пирамиды является прямоугольный треугольник с катетом a и прилежащим острым углом α. Две боковые грани пирамиды, содержащие катеты этого треугольника, перпендикулярны плоскости основания, а третья наклонена к ней под углом β. Найдите объём пирамиды.
5. В правильной четырёхугольной пирамиде плоский угол при вершине равен α. Найдите объём пирамиды, если её высота равна h.
Вариант 3
1. Основание прямой треугольной призмы – треугольник со сторонами 4![]() см и 6 см и углом 60° между ними. Высота призмы равна 2 см. Найдите объём призмы.
см и 6 см и углом 60° между ними. Высота призмы равна 2 см. Найдите объём призмы.
2. Найдите объём правильной четырёхугольной пирамиды, апофема которой равна 16 см и образует с плоскостью основания угол 30°.
3. Найдите объём правильной усечённой треугольной пирамиды, стороны оснований которой равны 2 см и 10 см, а высота – 6 см.
4. Основанием пирамиды является прямоугольный треугольник с катетом b и противолежащим острым углом β. Две боковые грани пирамиды, содержащие катеты этого треугольника, перпендикулярны плоскости основания, а третья наклонена к ней под углом α. Найдите объём пирамиды.
5. В правильной четырёхугольной пирамиде угол между боковым ребром и стороной основания равен α. Найдите объём пирамиды, если её высота равна h.
Вариант 4
1. Основание прямой четырёхугольной призмы – прямоугольник со сторонами 4 см и 7 см. Высота призмы равна 3 см. Найдите объём призмы.
2. Найдите объём правильной четырёхугольной пирамиды, боковое ребро которой равно 20 см и образует с высотой пирамиды угол 45°.
3. Найдите объём правильной усечённой четырёхугольной пирамиды, стороны оснований которой равны 3 см и 9 см, а высота – 5 см.
4. Основанием пирамиды является равнобедренный треугольник с радиусом описанной окружности R и углом α при вершине. Две боковые грани пирамиды, содержащие стороны этого угла, перпендикулярны плоскости основания, а третья наклонена к ней под углом β. Найдите объём пирамиды.
5. В правильной треугольной пирамиде угол между боковым ребром и стороной основания, имеющей с ним общую вершину, равен α. Найдите объём пирамиды, если её высота равна h.
Контрольная работа № 5 по теме «Объёмы тел вращения. Площадь сферы»
Вариант 1
1. Высота цилиндра равна 5![]() см, а диагональ осевого сечения образует с плоскостью основания угол 30°. Найдите объём цилиндра.
см, а диагональ осевого сечения образует с плоскостью основания угол 30°. Найдите объём цилиндра.
2. Образующая конуса равна 26 см, а его высота – 24 см. Найдите объём конуса.
3. Объёмы двух шаров относятся как 8 : 125. Найдите отношение площадей их поверхностей.
4. В нижнем основании цилиндра проведена хорда, которая находится на расстоянии d от центра верхнего основания и которая видна из этого центра под углом ![]() . Отрезок, соединяющий центр верхнего основания с точкой окружности нижнего основания, образует с плоскостью основания угол β. Найдите объём цилиндра.
. Отрезок, соединяющий центр верхнего основания с точкой окружности нижнего основания, образует с плоскостью основания угол β. Найдите объём цилиндра.
5. Основанием пирамиды является ромб со стороной 16 см и углом 60°. Двугранные углы пирамиды при рёбрах основания равны 30°. Найдите объём конуса, вписанного в данную пирамиду.
Вариант 2
1. Радиус основания цилиндра равен 2![]() см, а диагональ осевого сечения образует с плоскостью основания угол 45°. Найдите объём цилиндра.
см, а диагональ осевого сечения образует с плоскостью основания угол 45°. Найдите объём цилиндра.
2. Образующая конуса равна 17 см, а диаметр его основания – 16 см. Найдите объём конуса.
3. Площади поверхностей двух шаров относятся как 4 : 9. Найдите отношение их объёмов.
4. В нижнем основании цилиндра проведена хорда, длина которой равна b. Эта хорда видна из центра нижнего основания под углом β, а отрезок, соединяющий центр верхнего основания с серединой проведённой хорды, образует с плоскостью основания угол α. Найдите объём цилиндра.
5. Основанием пирамиды является равнобедренный треугольник с боковой стороной 20 см и основанием 24 см. Двугранные углы пирамиды при рёбрах основания равны 45°. Найдите объём конуса, вписанного в данную пирамиду.
Вариант 3
1. Диагональ осевого сечения цилиндра равна 8![]() см и образует с плоскостью основания угол 45°. Найдите объём цилиндра.
см и образует с плоскостью основания угол 45°. Найдите объём цилиндра.
2. Образующая конуса равна 25 см, а диаметр его основания – 30 см. Найдите объём конуса.
3. Объёмы двух шаров относятся как 27 : 64. Найдите отношение площадей их поверхностей.
4. В нижнем основании цилиндра проведена хорда, которая видна из центра этого основания под углом α. Отрезок, соединяющий центр верхнего основания с серединой этой хорды, равен b и образует с плоскостью основания угол β. Найдите объём цилиндра.
5. Основанием пирамиды является прямоугольный треугольник с катетами 6 см и
8 см. Двугранные углы пирамиды при рёбрах основания равны 60°. Найдите объём конуса, вписанного в данную пирамиду.
Вариант 4
1. Высота цилиндра равна 12![]() см, а диагональ осевого сечения образует с плоскостью основания угол 60°. Найдите объём цилиндра.
см, а диагональ осевого сечения образует с плоскостью основания угол 60°. Найдите объём цилиндра.
2. Образующая конуса равна 15 см, а его высота – 9 см. Найдите объём конуса.
3. Площади поверхностей двух шаров относятся как 9 : 25. Найдите отношение их объёмов.
4. В нижнем основании цилиндра проведена хорда, которая находится на расстоянии d от центра верхнего основания и стягивает дугу, градусная мера которой равна α, 0° . Найдите объём цилиндра.
5. Основанием пирамиды является прямоугольный треугольник с гипотенузой
30 см и катетом 18 см. Двугранные углы пирамиды при рёбрах основания равны 30°. Найдите объём конуса, вписанного в данную пирамиду.
Контрольная работа № 6 по теме «Обобщение и систематизация знаний учащихся»
Вариант 1
1. Даны точки A (1; 5; 8), B (5; 2; 9), C (7; 4; 7), D (8; 3; 0). Докажите, что прямая AB перпендикулярна плоскости BCD.
2. Через вершину конуса проведена плоскость под углом α к плоскости основания. Эта плоскость пересекает основание конуса по хорде, которая видна из центра основания под углом β. Радиус основания конуса равен R. Найдите площадь сечения конуса данной плоскостью.
3. Диагональ основания правильной четырёхугольной пирамиды равна d, а двугранный угол пирамиды при ребре основания равен α. Найдите объём пирамиды.
4. Основание прямой призмы – равнобедренный треугольник с основанием a и углом при вершине α. Диагональ боковой грани призмы, содержащей основание равнобедренного треугольника, наклонена к плоскости основания под углом β. Найдите:
1) объём призмы;
2) площадь боковой поверхности цилиндра, описанного около призмы.
5. Основание пирамиды – прямоугольный треугольник с острым углом α. Все боковые рёбра пирамиды наклонены к плоскости основания под углом β. Найдите объём пирамиды, если радиус сферы, описанной около неё, равен R.
Вариант 2
1. Даны точки A (2; 2; 1), B (3; 5; 4), C (−1; −10; −14), D (−4; 6; −1). Докажите, что прямая AD перпендикулярна плоскости ABC.
2. Через вершину конуса проведена плоскость под углом β к плоскости основания. Эта плоскость пересекает основание конуса по хорде длиной a, которая видна из центра основания под углом α. Найдите площадь сечения конуса данной плоскостью.
3. Высота правильной четырёхугольной пирамиды равна h, а двугранный угол пирамиды при ребре основания равен α. Найдите объём пирамиды.
4. Основание прямой призмы – равнобедренный треугольник с углом α при основании. Диагональ боковой грани призмы, содержащей боковую сторону основания, равна d и наклонена к плоскости основания под углом β. Найдите:
1) объём призмы;
2) площадь боковой поверхности цилиндра, описанного около призмы.
5. Основание пирамиды – равнобедренный треугольник с углом α при вершине. Все боковые рёбра пирамиды наклонены к плоскости основания под углом β. Найдите объём пирамиды, если радиус сферы, описанной около неё, равен R.
Вариант 3
1. Даны точки A (12; −9; −4), B (4; −5; 8), C (2; −3; 6), D (−1; −13; 5). Докажите, что прямая BC перпендикулярна плоскости ABD.
2. Через вершину конуса проведена плоскость под углом α к плоскости основания. Эта плоскость пересекает основание конуса по хорде, которая видна из центра основания под углом β. Высота конуса равна h. Найдите площадь сечения конуса данной плоскостью.
3. Высота правильной треугольной пирамиды равна h, а двугранный угол пирамиды при ребре основания равен α. Найдите объём пирамиды.
4. Основание прямой призмы – прямоугольный треугольник с катетом a и противолежащим углом α. Диагональ боковой грани призмы, содержащей гипотенузу основания, наклонена к плоскости основания под углом β. Найдите:
1) объём призмы;
2) площадь боковой поверхности цилиндра, описанного около призмы.
5. Основание пирамиды – равнобедренный треугольник с углом α при основании. Двугранные углы пирамиды при рёбрах основания равны β. Найдите объём пирамиды, если радиус вписанной в неё сферы равен r.
Вариант 4
1. Даны точки A (0; −1; 2), B (1; −2; 3), C (3; 2; −2), D (1; 6; 8). Докажите, что прямая AD перпендикулярна плоскости ABC.
2. Через две образующие конуса, угол между которыми равен α, проведена плоскость, пересекающая основание конуса по хорде, которая видна из центра основания под углом β. Радиус основания конуса равен R. Найдите площадь сечения конуса данной плоскостью.
3. Апофема правильной треугольной пирамиды равна b, а двугранный угол пирамиды при ребре основания равен α. Найдите объём пирамиды.
4. Основание прямой призмы – прямоугольный треугольник с гипотенузой c и острым углом α. Диагональ боковой грани призмы, содержащей катет, противолежащий углу α, наклонена к плоскости основания под углом β. Найдите:
1) объём призмы;
2) площадь боковой поверхности цилиндра, описанного около призмы.
5. Основание пирамиды – равнобедренный треугольник с углом α при вершине. Двугранные углы пирамиды при рёбрах основания равны β. Найдите объём пирамиды, если радиус вписанной в неё сферы равен r.
|
№ урока п/п | № урока в теме | Наименование раздела и тем | Дата по программе | Дата фактически | Примечание | ||
| 1 четверть | |||||||
|
Избранные вопросы планиметрии (15 часов)
| |||||||
| 1 | 1 | Решение треугольников. | 4.09 |
|
| ||
| 2 | 2 | Решение треугольников. | 8.09 |
|
| ||
| 3 | 3 | Вычисление биссектрис и медиан треугольника | 11.09 |
|
| ||
| 4 | 4 | Вычисление биссектрис и медиан треугольника | 15.09 |
|
| ||
| 5 | 5 | Формула Герона и другие формулы для площади треугольника | 18.09 |
|
| ||
| 6 | 6 | Формула Герона и другие формулы для площади треугольника. Тестовый контроль «Площади треугольника» | 22.09 |
|
| ||
| 7 | 7 | Теорема Чевы. Теорема Менелая. | 25.09 |
|
| ||
| 8 | 8 | Свойства и признаки вписанных и описанных четырёхугольников | 29.09 |
|
| ||
| 9 | 9 | Свойства и признаки вписанных и описанных четырёхугольников | 2.10 |
|
| ||
| 10 | 10 | Углы в окружности. Метрические соотношения в окружности | 6.10 |
|
| ||
| 11 | 11 | Геометрические места точек в задачах на построение. | 9.10 |
|
| ||
| 12 | 12 | Геометрические преобразования в задачах на построение | 13.10 |
|
| ||
| 13 | 13 | Геометрические преобразования в задачах на построение | 16.10 |
|
| ||
| 14 | 14 | О разрешимости задач на построение. Эллипс, гипербола, парабола. | 20.10 |
|
| ||
| 15 | 15 | О разрешимости задач на построение. Эллипс, гипербола, парабола. | 23.10 |
|
| ||
|
Глава 1. Аксиомы стереометрии и их простейшие следствия(5 часов)
| |||||||
| 16 | 1 | Аксиомы стереометрии | 27.10 |
|
| ||
| 2 четверть | |||||||
| 17 | 2 | Существование плоскости, проходящей через данную прямую и данную точку. Замечание к аксиоме 1. | 6.11 |
|
| ||
| 18 | 3 | Пересечение прямой с плоскостью | 10.11 |
|
| ||
| 19 | 4 | Существование плоскости, проходящей через три данные точки | 13.11 |
|
| ||
| 20 | 5 | Существование плоскости, проходящей через три данные точки | 17.11 |
|
| ||
|
Глава 2. Параллельность прямых и плоскостей (12 часов)
| |||||||
| 21 | 1 | Параллельные прямые в пространстве | 20.11 |
|
| ||
| 22 | 2 | Признак параллельности прямых | 24.11 |
|
| ||
| 23 | 3 | Признак параллельности прямых | 27.11 |
|
| ||
| 24 | 4 | Контрольная работа №1 « Аксиомы стереометрии. Параллельные прямые в пространстве» | 1.12 |
|
| ||
| 25 | 5 | Признак параллельности прямой и плоскости | 4.12 |
|
| ||
| 26 | 6 | Признак параллельности прямой и плоскости | 8.12 |
|
| ||
| 27 | 7 | Признак параллельности плоскостей | 11.12 |
|
| ||
| 28 | 8 | Существование плоскости, параллельной данной плоскости. | 15.12 |
|
| ||
| 29 | 9 | Свойства параллельных плоскостей | 18.12 |
|
| ||
| 30 | 10 | Изображение пространственных фигур на плоскости | 22.12 |
|
| ||
| 31 | 11 | Изображение пространственных фигур на плоскости | 25.12 |
|
| ||
| 32 | 12 | Контрольная работа №2 « Параллельность прямых и плоскостей» | 29.12 |
|
| ||
| 3 четверть | |||||||
|
Глава 3. Перпендикулярность прямых и плоскостей(15 часов)
| |||||||
| 33 | 1 | Перпендикулярность прямых в пространстве | 15.01 |
|
| ||
| 34 | 2 | Признак перпендикулярности прямой и плоскости | 19.01 |
|
| ||
| 35 | 3 | Построение перпендикулярных прямой и плоскости | 22.01 |
|
| ||
| 36 | 4 | Свойства перпендикулярных прямой и плоскости | 26.01 |
|
| ||
| 37 | 5 | Перпендикуляр и наклонная | 29.01 |
|
| ||
| 38 | 6 | Перпендикуляр и наклонная | 2.02 |
|
| ||
| 39 | 7 | Перпендикуляр и наклонная | 5.02 |
|
| ||
| 40 | 8 | Перпендикуляр и наклонная | 9.02 |
|
| ||
| 41 | 9 | Перпендикуляр и наклонная | 12.02 |
|
| ||
| 42 | 10 | Теорема о трёх перпендикулярах | 16.02 |
|
| ||
| 43 | 11 | Теорема о трёх перпендикулярах | 19.02 |
|
| ||
| 44 | 12 | Признак перпендикулярности плоскостей | 26.02 |
|
| ||
| 45 | 13 | Признак перпендикулярности плоскостей
| 2.03 |
|
| ||
| 46 | 14 | Расстояние между скрещивающимися прямыми | 5.03 |
|
| ||
| 47 | 15 | Контрольная работа №3 « Перпендикулярность прямых и плоскостей» | 9.03 |
|
| ||
|
Глава 4. Декартовы координаты и векторы в пространстве (18 часов)
| |||||||
| 48 | 1 | Введение декартовых координат в пространстве. Расстояние между точками | 12.03 |
|
| ||
| 49 | 2 | Координаты середины отрезка | 16.03 |
|
| ||
| 50 | 3 | Преобразование симметрии в пространстве. Симметрия в природе и на практике | 19.03 |
|
| ||
| 51 | 4 | Движение в пространстве. Параллельный перенос в пространстве. Подобие пространственных фигур. | 23.03 |
|
| ||
| 4 четверть | |||||||
| 52 | 5 | Угол между скрещивающимися прямыми | 6.04 |
|
| ||
| 53 | 6 | Угол между прямой и плоскостью. | 9.04 |
|
| ||
| 54 | 7 | Угол между плоскостями | 13.04 |
|
| ||
| 55 | 8 | Площадь ортогональной проекции многоугольника | 16.04 |
|
| ||
| 56 | 9 | Векторы в пространстве | 20.04 |
|
| ||
| 57 | 10 | Действия над векторами в пространстве | 23.04 |
|
| ||
| 58 | 11 | Действия над векторами в пространстве | 27.04 |
|
| ||
| 59 | 12 | Действия над векторами в пространстве | 30.04 |
|
| ||
| 60 | 13 | Разложение вектора по трём некомпланарным векторам | 4.05 |
|
| ||
| 61 | 14 | Разложение вектора по трём некомпланарным векторам | 7.05 |
|
| ||
| 62 | 15 | Уравнение плоскости | 11.05 |
|
| ||
| 63 | 16 | Уравнение плоскости | 14.05 |
|
| ||
| 64 | 17 | Уравнение плоскости | 18.05 |
|
| ||
| 65 | 18 | Контрольная работа №4 « Декартовы координаты и векторы в пространстве» | 21.05 |
|
| ||
| Повторение (2 часа) | |||||||
| 66 | 1 | Повторение | 25.05 |
|
| ||
| 67 | 2 | Повторение | 28.05 |
|
| ||
| 68 | 1 | Итоговая контрольная работа | 30.05 |
|
| ||
© 2021, Жамбалова Виктория Батоцыреновна 3115 26
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы
Полезное для учителя
























