Муниципальное бюджетное общеобразовательное учреждение
«Селиховская средняя общеобразовательная школа»
Курской области Курского района
Рассмотрена на заседании ШМО Принята на заседании ПС «Утверждаю»
Протокол №1 Протокол №1 Директор школы
от «___» августа 2021 г. от « » _________ 2021 г. __________/Н.В. Охотникова/
Руководитель ШМО Председатель ПС Приказ № _____
_____________/___________/ __________ /Л.В. Срывкова/ от «_____»__________2021 г.
Рабочая программа учебного предмета
«Алгебра»
для 7 класса
основное общее образование
Срок реализации: 1 год
Программа составлена учителем математики Митиной Д. Е.
д. Селиховы Дворы
2021 - 2022 учебный год
Пояснительная записка
Рабочая программа по алгебре для 7 класса соответствует базовому уровню изучения предмета, составлена на основе и соответствует требованиям:
Федерального Закона от 29.12.2012 № 273-ФЗ «Об образовании в Российской Федерации»;
Федерального государственного образовательного стандарта основного общего образования, утвержденного приказом Министерства образования и науки Российской Федерации от 17.12.2010 № 1897 (далее – ФГОС основного общего образования);
Порядка организации и осуществления образовательной деятельности по основным общеобразовательным программам – образовательным программам основного общего образования, утвержденного приказом Министерства образования и науки Российской Федерации от 30.08.2013 № 1015;
Основной образовательной программы общего образования МБОУ «Селиховская средняя общеобразовательная школа» 2020-2025г.г. с изменениями и дополнениями.
Федерального перечня учебников, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования, утвержденного приказом Министерства просвещения Российской Федерации от 28.12.2018 № 345;
Санитарно-эпидемиологических требований к условиям и организации обучения в общеобразовательных учреждениях, утвержденных постановлением Главного государственного санитарного врача Российской Федерации 1.2.3685-21;
7.Письма Роспотребнадзора N 02/16587-2020-24, Минпросвещения России N ГД-1192/03 от 12.08.2020 "Об организации работы общеобразовательных организаций";
Цели обучения предмету
овладевать системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
формировать интеллектуальное развитие, интерес к предмету «математика», качества личности, необходимые человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
формировать представление об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитывать культуру личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.
Задачи обучения предмету :
развитие представление о числе и роли вычислений в человеческой практике; формирование практических навыков выполнения устных, письменных, инструментальных вычислений, развитие вычислительной культуры;
овладение символическим языком алгебры, выработка формально-оперативные алгебраических умений и применение их к решению математических и нематематических задач;
изучение свойств и графиков элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
получение представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
развитие логического мышления и речи – умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
формирование представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
УМК, Ю.Н. Макарычева и других. 7 – 9 классы: пособие для учителей общеобразовательных организаций. – Москва: «Просвещение», 2014г и учебника для общеобразовательных учреждений Алгебра 7 класс. /Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова/; под редакцией С. А. Теляковского. – М.: Просвещение, 2017;
Планируемые результаты освоения учебного предмета
Личностные результаты
У обучающегося сформируется:
нормы поведения в рамках межличностных отношений,
правосознание;
ориентация в нравственном содержании и смысле поступков как собственных, так и окружающих людей;
основы гражданской идентичности личности в форме осознания «Я» как гражданина России, чувства
сопричастности и гордости за свою Родину, народ и историю, осознание ответственности человека за общее
благополучие, осознание своей этнической принадлежности;
социальные нормы, правила поведения, роли и формы социальной жизни в группах и сообществах, включая
взрослые и социальные сообщества;
Обучающийся получит возможность для формирования:
морального сознания на конвенциональном уровне,
способности к решению моральных дилемм на основе учета позиций партнеров в общении, ориентации на их мотивы и чувства, устойчивое следование в поведении моральным нормам и этическим требованиям.
Метапредметные результаты
Познавательные УУД
Обучающийся научится:
• осуществлять анализ объектов с выделением существенных
и несущественных признаков;
• осуществлять синтез как составление целого из частей;
• проводить сравнение и классификацию по заданным критериям.
Обучающийся получит возможность научиться:
осуществлять синтез как составление целого из частей,
самостоятельно достраивая и восполняя недостающие
компоненты;
осуществлять сравнение и классификацию, самостоятельно выбирая основания и критерии для указанных логических операций.
Регулятивные УУД
Обучающийся научится:
адекватной ретроспективной оценки;
Обучающийся получит возможность научиться:
осуществлять констатирующий и предвосхищающий контроль по результату и по способу действия, актуальный контроль на уровне произвольного внимания.
Коммуникативные УУД
Обучающийся научится:
точек зрения, в том числе не совпадающих с его собственной, и ориентироваться на позицию партнера в общении и взаимодействии;
договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов.
Обучающийся получит возможность научиться:
действовать с учетом позиции другого и уметь согласовывать свои действия;
устанавливать и поддерживать необходимые контакты с другими людьми, владея нормами и техникой общения.
Предметные результаты
РАЦИОНАЛЬНЫЕ ЧИСЛА
Ученик научится:
1) понимать особенности десятичной системы счисления;
2) владеть понятиями, связанными с делимостью натуральных чисел;
3) выражать числа в эквивалентных формах, выбирая наиболее подходящую в зависимости от конкретной ситуации;
4) сравнивать и упорядочивать рациональные числа;
5) выполнять вычисления с рациональными числами, сочетая устные и письменные приемы вычислений, применение калькулятора;
6) использовать понятия и умения, связанные с пропорциональностью величин, процентами в ходе решения математических задач и задач из смежных предметов, выполнять несложные практические расчеты.
Ученик получит возможность:
1) познакомиться с позиционными системами счисления с основаниями, отличными от 10;
2) углубить и развить представления о натуральных числах и свойствах делимости;
3) научится использовать приемы, рационализирующие вычисления, приобрести привычку контролировать вычисления, выбирая подходящий для ситуации способ.
АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ
Ученик научится:
1) владеть понятиями «тождество», «тождественное преобразование», решать задачи, содержащие буквенные данные; работать с формулами;
2) выполнять преобразования выражений, содержащих степени с натуральным показателем;
3) выполнять тождественные преобразования рациональных выражений на основе правил действий над многочленами;
4) выполнять разложение многочленов на множители.
Ученик получит возможность:
1) научится выполнять многошаговые преобразования рациональных выражений, применяя широкий набор способов и приемов;
2) применять тождественные преобразования для решения задач из различных разделов курса.
УРАВНЕНИЯ
Ученик научится:
1) решать линейные уравнения с одной переменной, системы двух уравнений с двумя переменными;
2) понимать уравнение как важную математическую модель для описания и изучения разнообразных реальных ситуаций, решать текстовые задачи алгебраическим методом;
3) применять графические представления для исследования уравнений, исследование и решение систем уравнений с двумя переменными.
Ученик получит возможность:
1) овладеть специальными приемами решения уравнений и систем уравнений; уверенно применять аппарат уравнений; уверенно применять аппарат уравнений для решения разнообразных задач из математики, смежных предметов, практики;
2) применять графические представления для исследования уравнений, систем уравнений, содержащих буквенные коэффициенты.
ОСНОВНЫЕ ПОНЯТИЯ. ЧИСЛОВЫЕ ФУНКЦИИ
Ученик научится:
1) понимать и использовать функциональные понятия и язык (термины, символические обозначения);
2) строить графики элементарных функций; исследовать свойства числовых функций на основе изучения поведения их графиков;
3) понимать функцию как важнейшую математическую модель для описания процессов и явлений окружающего мира, применять функциональный язык для описания и исследования зависимостей между физическими величинами.
Ученик получит возможность научиться:
1) проводить исследования, связанные с изучением свойств функции, в том числе с использованием компьютера; на основе графиков изученных функций строить более сложные графики (кусочно-заданные, с «выколотыми» точками и т.п.);
2) использовать функциональные представления и свойства функций для решения математических задач из различных разделов.
Содержание учебного предмета
| № | Наименования разделов, тем | Кол-во часов | Текущая и промежуточная аттестация |
| 1 | Выражения, тождества, уравнения | 22 |
|
|
| Выражения Преобразование выражений Уравнения с одной переменной Статистические характеристики Обобщение и систематизация знаний. Контроль | 4 5 7 4 2 | Входная контрольная работа Контрольная работа №1 «Выражения. Тождества» Контрольная работа №2 «Уравнение с одной переменной» |
| 2 | Функции | 11 |
|
|
| Функции и их графики Линейная функция Обобщение и систематизация знаний. Контроль | 5 5 1 | Контрольная работа №3 «Линейная функция» |
| 3 | Степень с натуральным показателем | 11 |
|
|
| Степень и её свойства Одночлены Обобщение и систематизация знаний. Контроль | 5 5 1 | Контрольная работа №4 «Степень с натуральным показателем» |
| 4 | Многочлены | 17 |
|
|
| Сумма и разность многочленов Произведение одночлена и многочлена Произведение многочленов Обобщение и систематизация знаний. Контроль | 3 5 7 2 | Контрольная работа №5 «Сложение и вычитание многочленов» Контрольная работа №6 «Произведение многочленов» |
| 5 | Формулы сокращенного умножения | 18 |
|
|
| Квадрат суммы и квадрат разности Разность квадратов. Сумма и разность кубов Преобразование целых выражений Обобщение и систематизация знаний. Контроль | 6 5 5 2 | Контрольная работа №7 «Формулы сокращенного умножения» |
| 6 | Системы линейных уравнений | 17 |
|
|
| Линейные уравнения с двумя переменными и их системы Решение систем линейных уравнений Обобщение и систематизация знаний. Контроль | 6
9 2 | Контрольная работа №8 «Преобразование целого выражения в многочлен» Контрольная работа №9 «Системы линейных уравнений» |
| 7 | Повторение | 6 |
|
|
| Обобщение и систематизация знаний. Контроль | 1 | Итоговая контрольная работа |
|
| Итого | 102 | 11 |
Календарно - тематический план
| № п/п | Дата план | Дата факт | Наименование разделов, тем уроков | Кол-во часов |
| Глава 1. Выражения, тождества, уравнение. (22 урока) |
| 1 |
|
| Числовые выражения | 1 |
| 2 |
|
| Нахождение значений числовых выражений | 1 |
| 3 |
|
| Сравнение значений выражений | 1 |
| 4 |
|
| Сравнение значений выражений. Двойные неравенства | 1 |
| 5 |
|
| Свойства действий над числами | 1 |
| 6 |
|
| Входная контрольная работа | 1 |
| 7 |
|
| Тождества. | 1 |
| 8 |
|
| Тождественные преобразования выражений | 1 |
| 9 |
|
| Свойства действий над числами. Тождественные преобразования | 1 |
| 10 |
|
| Контрольная работа №1 «Выражения. Тождества» | 1 |
| 11 |
|
| Уравнение и его корни | 1 |
| 12 |
|
| Уравнение и его корни. Равносильные уравнения | 1 |
| 13 |
|
| Линейное уравнение с одной переменной | 1 |
| 14 |
|
| Линейные уравнения и уравнения, сводящиеся к ним | 1 |
| 15 |
|
| Решение задач на движение с помощью уравнений | 1 |
| 16 |
|
| Решение задач на проценты с помощью уравнений | 1 |
| 17 |
|
| Линейное уравнение с одной переменной, решение задач с помощью уравнений | 1 |
| 18 |
|
| Среднее арифметическое, размах и мода | 1 |
| 19 |
|
| Нахождение статистических характеристик | 1 |
| 20 |
|
| Медиана как статистическая характеристика | 1 |
| 21 |
|
| Нахождение медианы ряда | 1 |
| 22 |
|
| Контрольная работа №2 «Уравнение с одной переменной» | 1 |
| Глава 2. Функции. (11 уроков) |
| 23 |
|
| Что такое функция | 1 |
| 24 |
|
| Вычисление значений функций по формуле | 1 |
| 25 |
|
| Вычисление значений функций по графику | 1 |
| 26 |
|
| График функции | 1 |
| 27 |
|
| Чтение графика функции | 1 |
| 28 |
|
| Прямая пропорциональность и ее график | 1 |
| 29 |
|
| Угловой коэффициент | 1 |
| 30 |
|
| Прямая пропорциональность и ее график. Решение задач | 1 |
| 31 |
|
| Линейная функция и ее график | 1 |
| 32 |
|
| Взаимное расположение графиков линейных функций | 1 |
| 33 |
|
| Контрольная работа №3 «Линейная функция» | 1 |
| Глава 3. Степень с натуральными показателями. (11 уроков) |
| 34 |
|
| Определение степени с натуральным показателем | 1 |
| 35 |
|
| Умножение и деление степеней | 1 |
| 36 |
|
| Преобразование алгебраических выражений с помощью основных свойств степени | 1 |
| 37 |
|
| Возведение в степень произведения и степени | 1 |
| 38 |
|
| Упрощение выражений со степенями | 1 |
| 39 |
|
| Одночлен и его стандартный вид | 1 |
| 40 |
|
| Умножение одночленов. | 1 |
| 41 |
|
| Возведение одночлена в натуральную степень | 1 |
| 42 |
|
| Функции у = х2 и у = х3 графики функций | 1 |
| 43 |
|
| Решение уравнений графическим способом | 1 |
| 44 |
|
| Контрольная работа №4 «Степень с натуральным показателем» | 1 |
| Глава 4. Многочлены. (17 уроков) |
| 45 |
|
| Многочлен и его стандартный вид | 1 |
| 46 |
|
| Приведение многочлена к стандартному виду | 1 |
| 47 |
|
| Действия с многочленами | 1 |
| 48 |
|
| Умножение одночлена на многочлен | 1 |
| 49 |
|
| Решение уравнений с многочленами | 1 |
| 50 |
|
| Вынесение общего множителя за скобки | 1 |
| 51 |
|
| Вынесение общего множителя за скобки. Решение задач | 1 |
| 52 |
|
| Разложение многочленов на множители | 1 |
| 53 |
|
| Контрольная работа №5 «Сложение и вычитание многочленов» | 1 |
| 54 |
|
| Умножение многочлена на многочлен | 1 |
| 55 |
|
| Решение уравнений и задач на применение правила умножения многочлена на многочлен | 1 |
| 56 |
|
| Доказательство тождества многочленов | 1 |
| 57 |
|
| Способ группировки | 1 |
| 58 |
|
| Разложение многочлена на множители способом группировки | 1 |
| 59 |
|
| Разложение на множители трехчлена | 1 |
| 60 |
|
| Разложение многочлена на множители способом группировки. Решение задач | 1 |
| 61 |
|
| Контрольная работа №6 «Произведение многочленов». | 1 |
| Глава 5. Формулы сокращенного умножения. (18 уроков) |
| 62 |
|
| Основные формулы сокращенного умножения: квадрат суммы и квадрат разности. | 1 |
| 63 |
|
| Возведение в квадрат суммы и разности двух выражений | 1 |
| 64 |
|
| Возведение в куб суммы и разности двух выражений | 1 |
| 65 |
|
| Разложение на множители с помощью формул квадрата суммы и квадрата разности | 1 |
| 66 |
|
| Представление многочлена в виде произведения | 1 |
| 67 |
|
| Формула сокращенного умножения - разность квадратов. | 1 |
| 68 |
|
| Умножение разности двух выражений на их сумму | 1 |
| 69 |
|
| Формула разности квадратов | 1 |
| 70 |
|
| Разложение многочленов на множители с помощью формулы разности квадратов | 1 |
| 71 |
|
| Разложение разности квадратов на множители | 1 |
| 72 |
|
| Разложение на множители суммы и разности кубов. | 1 |
| 73 |
|
| Контрольная работа №7 «Формулы сокращенного умножения» | 1 |
| 74 |
|
| Преобразование целого выражения в многочлен | 1 |
| 75 |
|
| Применение формул сокращенного умножение при преобразовании целого выражения в многочлен | 1 |
| 76 |
|
| Решение уравнений. Доказательство тождеств. Задачи на делимость | 1 |
| 77 |
|
| Способы разложения многочленов на множители | 1 |
| 78 |
|
| Применение различных способов для разложения на множители | 1 |
| 79 |
|
| Обобщающий урок по теме «Преобразование целого выражения в многочлен» | 1 |
| Глава 6. Системы линейных уравнений. (17 уроков) |
| 80 |
|
| Линейное уравнение с двумя переменными | 1 |
| 81 |
|
| Выражение одной переменной через другую в линейном уравнении | 1 |
| 82 |
|
| Контрольная работа №8 «Преобразование целого выражения в многочлен» | 1 |
| 83 |
|
| График линейного уравнения с двумя переменными | 1 |
| 84 |
|
| Решение уравнений с двумя переменными | 1 |
| 85 |
|
| Системы линейных уравнений с двумя переменными | 1 |
| 86 |
|
| Графическое решение системы линейных уравнений с двумя переменными | 1 |
| 87 |
|
| Способ подстановки | 1 |
| 88 |
|
| Решение системы уравнений способом подстановки | 1 |
| 89 |
|
| Способ сложения | 1 |
| 90 |
|
| Способ сложения. Решение систем | 1 |
| 91 |
|
| Решение системы уравнений способом сложения | 1 |
| 92 |
|
| Решение задач с помощью систем уравнений | 1 |
| 93 |
|
| Решение задач на движение с помощью систем уравнений | 1 |
| 94 |
|
| Решение задач на работу с помощью систем уравнений | 1 |
| 95 |
|
| Контрольная работа №9 «Системы линейных уравнений» | 1 |
| 96 |
|
| Решение задач. Обобщающий урок «Системы линейных уравнений» | 1 |
| Повторение. (9 часов) |
| 97 |
|
| Уравнения с одной переменной | 1 |
| 98 |
|
| Линейная функция | 1 |
| 99 |
|
| Итоговая контрольная работа | 1 |
| 100 |
|
| Степень с натуральным показателем и ее свойства | 1 |
| 101 |
|
| Сумма и разность многочленов. Произведение одночлена и многочлена. Произведение многочленов | 1 |
| 102 |
|
| Системы линейных уравнений | 1 |
| 103 |
|
| Преобразование целого выражения. | 1 |
| 104 |
|
| Системы линейных уравнений | 1 |
| 105 |
|
| Обобщающий урок за курс 7 класса | 1 |
ПРИЛОЖЕНИЕ №1
к рабочей программе учебного предмета
«Алгебра»»
для 7 класса
основное общее образование
Тематическое планирование с учетом рабочей программы воспитания
| № | Наименование разделов, тем | Модуль воспитательной программы «Школьный урок» | Количество часов |
| 1 | Выражения, тождества, уравнения | День знаний. |
|
| 2 | Функции | Джордж Буль английский математик |
|
| 3 | Степень с натуральным показателем | день Российской науки |
|
| 4 | Многочлены | международный день числа «пи» |
|
| 5 | Формулы сокращенного умножения | Леонард Эйлер один из величайших математиков XVIII столетия |
|
| 6 | Системы линейных уравнений | Пафну́тий Льво́вич Чебышёв русский математик и механик, основоположник петербургской математической школы |
|
ПРИЛОЖЕНИЕ №2
к рабочей программе учебного предмета
«Алгебра»»
для 7 класса
основное общее образование
График промежуточной и итоговой аттестации по алгебре
| № | Текущая и промежуточная аттестация | Дата |
| 1 | Входная контрольная работа | 13.09.2021 |
| 2 | Контрольная работа №1 «Выражения. Тождества» | 22.09.2021 |
| 3 | Контрольная работа №2 «Уравнение с одной переменной» | 20.10.2021 |
| 4 | Контрольная работа №3 «Линейная функция» | 26.11.2021 |
| 5 | Контрольная работа №4 «Степень с натуральным показателем» | 22.12.2021 |
| 6 | Контрольная работа №5 «Сложение и вычитание многочленов» | 21.01.2022 |
| 7 | Контрольная работа №6 «Произведение многочленов» | 09.02.2022 |
| 8 | Контрольная работа №7 «Формулы сокращенного умножения» | 09.03.2022 |
| 9 | Контрольная работа №8 «Преобразование целого выражения в многочлен» | 11.04.2022 |
| 10 | Контрольная работа №9 «Системы линейных уравнений» | 11.05.2022 |
| 11 | Итоговая контрольная работа | 20.05.2022 |
Оценочные материалы для проведения аттестации
Входная контрольная работа по алгебре 7 класс
Вариант 1
1. Найдите значение выражения: а)2/15 +5/12 б) (-2 1/7). (-3,5)
2. Решите уравнение: а) - 2,4х + 0,6 = - 4,2; б) 7 · ( х + 4) = 21
3. Построить в координатной плоскости треугольник МКР, если М (– 6; – 3), К (– 2; 3), Р (6; 9).
4.В книге 240 страниц. Повесть занимает 60% книги, а рассказы 19/24 остатка. Сколько страниц в книге составляют рассказы?
5.На второй полке стояло в 4 раза больше книг, чем на первой. Когда на первую полку поставили еще 35 книг, а со второй убрали 25 книг, то на обоих полках книг стало поровну. Сколько книг было на каждой полке первоначально?
6. На машину погрузили а ящиков с виноградом по 20 кг в каждом и b ящиков с персиками по 12 кг в каждом. Составьте выражение для нахождения массы всех фруктов, погруженных на машину, и найдите её значение, если а =15, а b = 20.
7. Вычислите:(2,6·0,3- 2 4/15:5 2/3) : ( -1,9).
Вариант 2
1. Найдите значение выражения: а) 3/10-2/15 ; б) 2,4 · (-11/3 ).
2. Решите уравнение: а) - 3,6х + 0,8 = - 6,4; б) 6 · (х +5) = 18
3.Построить в координатной плоскости треугольник АВМ, если А(2; – 5), В(1; 4), М(– 6; 3)
4. Завод изготовил сверх плана 160 автомобилей. 3/4 этих автомобилей отправили строителям гидростанции, а 80% остатка – в рисоводческий совхоз. Сколько автомобилей было отправлено в рисоводческий совхоз?
5. В саду яблонь было в 3 раза больше, чем слив. После того, как 14 яблонь вырубили и посадили 10 слив, деревьев обоих видов в саду стало поровну. Сколько яблонь и сколько слив было в саду
6. Один килограмм масла стоит m рублей, а один килограмм творога n рублей. Составьте выражение для нахождения стоимости 3 кг масла и 2 кг творога вместе. Найдите значение этого выражения, если m =160 рублей, а n = 80 рублей.
7. Вычислите: (1,8 · 0,4 -2 8/15 : 6 1/3):( - 0,8).
Критерии оценивания:
«5» -если верно выполнены 6-7 задания;
«4»- если верно выполнены любые 4-5 задания;
«3» - если верно выполнено любое 3 задания;
«2» - если верно выполнено меньше 3 заданий.
Ответы:
Вариант 1 №1 а)0,55 б) 7,5 №2 а)2 б) -1 №4 76 стр №5 20 кн, 80 кн №6 20а+12в; 540 кг №7 -0,2
Вариант 2 №1 а)1/6 б) -3,2 №2 а)2 б) -2 №4 32 м №5 12 с, 36 яб №6 3m+2n; 640 р №7 -0,4
Контрольная работа №1 по алгебре «Выражения и тождества»
1 вариант
1.Упростить выражение
а) 5+ 2(х – 1); б) 2а – (3б – а) + (3б – 2а);
в)5(а – 3) – 3(3а – 5); г) 16с + (3с – 2) – (5с + 7).
2. Решите уравнение:
А) 2х-14=28; б)3.5а+10=1,5а+12
3. Упростите выражение: 6,3х – 4 – 3(7,2х + 0,3) и найдите его значение при 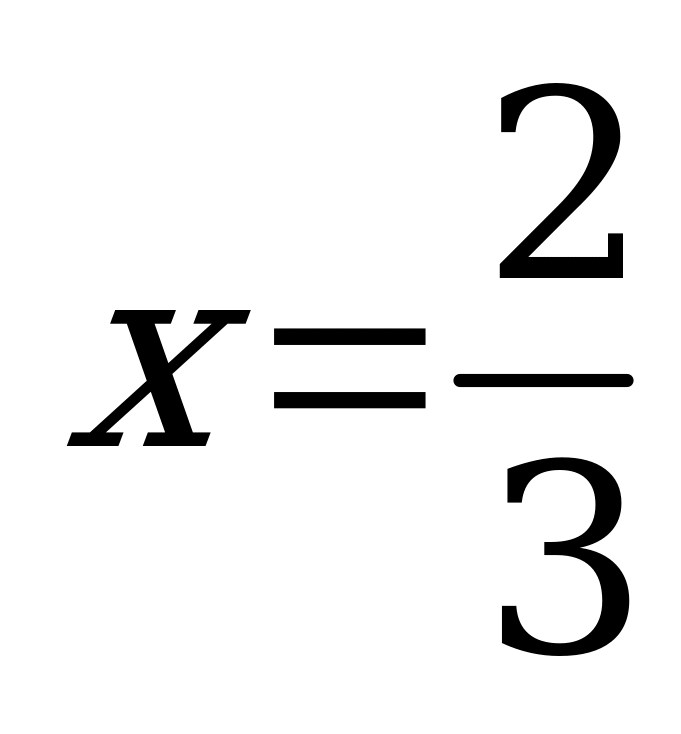 .
.
4. Катя купила а ручек по 3 руб. и 15 карандашей по b руб.
а) Сколько стоит Катина покупка?
б) Решите задачу при а = 4, b = 2,5.
5. Сравните значения выражений: 3 – 0,2а и 5 – 0,3а , при а = 16.
Контрольная работа по алгебре «Выражения и тождества» 7 класс
2 вариант
1.Упростить выражение
а) 12+3(х-2); б) 2а – (4б – а) + (4б – 3а);
в) 6(а – 2) – 3(2а – 5); г) 8а + (5 – а) – (7 + 11а)
2. Решите уравнение:
А) 3х-15=30; б)2,5а+8=1,5а+12,5
3. Упростите выражение: 3,2а – 7 – 7(2,1а – 0,3) и найдите его значение при 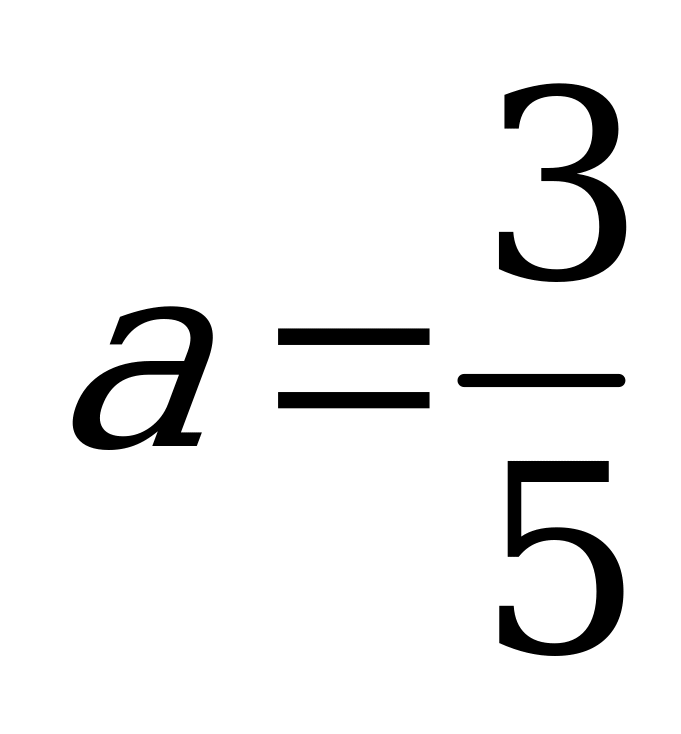 .
.
4. Мама купила х кг картофеля по 6 руб. за кг и 3 кг капусты по у руб. за кг.
а) На сколько больше заплатила мама за картофель, чем за капусту?
б) Решите задачу при х = 7, у = 8,5.
5. Сравните значения выражений: 0,5х – 4 и 0,6х – 3 при х = 5.
Вариант 1: 1)а) 2х-3, б) а, в) –а, г) 14с-9; 2)а) 21, б) 1; 3) 5.3; 4) 49,5; 5) меньше
Вариант 2: 1)а) 3х+12, б) 0, в) 3, г) -4а-2; 2)а) 15, б) 4.5; 3) -11,8; 4) 67.5; 5) меньше
Критерии оценивания:
«5» -если верно выполнены 5 задания;
«4»- если верно выполнены любые 4 задания;
«3» - если верно выполнено любые 3 задания;
«2» - если верно выполнено меньше 3 заданий.
Контрольная работа №2 по теме: «Линейные уравнения с одной переменной»
Вариант № 1
1. Решите уравнение:
а) 9х- 7 = 6х+14;
б) 3(4 - 2х) + 6 = -2х + 4.
2. В одном мешке было в 3 раза больше муки, чем в другом. Когда из первого мешка взяли 4 кг муки, а во второй добавили 2 кг, то в мешках муки стало поровну. Сколько килограммов муки было в каждом мешке сначала.
3. Решите уравнение:
14(х- 2) - 3х =5х- 4.;
4. Первой бригаде надо было отремонтировать 180 м дороги, а второй — 160 м. Первая бригада ремонтировала ежедневно 40 м дороги, а вторая — 25 м. Через сколько дней первой бригаде останется отремонтировать в 3 раза меньше метров дороги, чем второй?
5. При каком значении а уравнение (2 + а)х = 10 имеет корень, равный 5.
Вариант № 2
1. Решите уравнение:
а) 4(3х- 1) - 6х =5х+ 8;
б) 7х - 5(2х + 1) = 5х + 15.
2. В одном мешке было в 4 раза больше сахара, чем в другом. Когда из первого мешка взяли 10 кг сахара, а во второй досыпали 5 кг, то в мешках сахара стало поровну. Сколько килограммов сахара было в каждом мешке сначала?
3.Решите уравнение:
6(2х- 1) - 3х =7х- 4;
В одном контейнере было 200 кг яблок, а в другом — 120 кг. Из первого контейнера брали ежедневно по 30 кг, а из второго — по 25 кг. Через сколько дней в первом контейнере останется в 4 раза больше яблок, чем во втором?
При каком значении а уравнение (а - 3)х = 8 имеет корень, равный 4.
Вариант 1: 1)а) 7; б) 3.5; 2) 3; 3) 4; 4) 4; 5) 0.
Вариант 2: 1)а) 4; б) -2.5; 2) 5; 3) 1; 4) 4; 5) 0.
Критерии оценивания:
«5» -если верно выполнены 5 задания;
«4»- если верно выполнены любые 4 задания;
«3» - если верно выполнено любые 3 задания;
«2» - если верно выполнено меньше 3 заданий.
Контрольная работа №3 по теме «Линейная функция»
Вариант 1
1. Функция задана формулой у = 6х + 19. Определите:
а) значение у, если х = 1;
б) значение х, при котором у = 1;
в) проходит ли график функции через точку А (–2; 7).
2. а) Постройте график функции у = 2х – 4.
б) Укажите с помощью графика, чему равно значение у при х = 0.
3. В одной и той же системе координат постройте графики функций:
а) у = –2х; б) у = 3.
4. Найдите координаты точки пересечения графиков функций
у = 47х – 37 и у = –13х + 23.
5. Задайте формулой линейную функцию, график которой параллелен прямой у = 3х – 7 и проходит через начало координат.
Вариант 2
1. Функция задана формулой у = 4х – 30. Определите:
а) значение у, если х = 10;
б) значение х, при котором у = –6;
в) проходит ли график функции через точку В (7; –3).
2. а) Постройте график функции у = –3х + 3.
б) Укажите с помощью графика, при каком значении х значение у равно 6.
3. В одной и той же системе координат постройте графики функций:
а) у = 0,5х; б) у = –4.
4. Найдите координаты точки пересечения графиков функций
у = –38х + 15 и у = –21х – 36.
5. Задайте формулой линейную функцию, график которой параллелен прямой у = –5х + 8 и проходит через начало координат
Решение заданий контрольной работы
Вариант 1
1. а) 22; б) –3; в) проходит.
| 2. а) у = 2х – 4. Построим две точки, принадлежащие графику. Если х = 0, то у = 2 · 0 – 4 = –4; если х = 2, то у = 2 · 2 – 4 = 0. (0; –4), (2; 0). б) При х = 1,5 у = –1. | 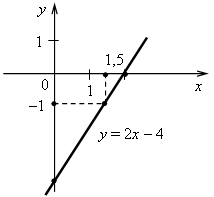
|
| 3. а) у = –2х. Графиком является прямая, проходящая через начало координат и точку (2; –4). б) у = 3. Графиком является прямая, проходящая через точку (0; 3) и параллельная оси х.
4. (1; 10). | 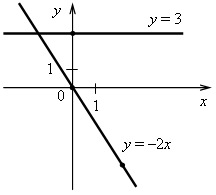
|
5. 3х.
Вариант 2
1. а) –40; б) 6; в) не проходит.
| 2. а) у = –3х + 3. Построим две точки, принадлежащие графику. Если х = 0, то у = –3 · 0 + 3 = 3; если х = 2, то у = –3 · 2 + 3 = –3; (0; 3), (2; –3)
б) Если у = 6, то х = –1. | 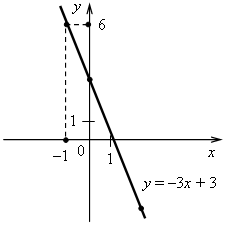
|
3. а) у = 0,5х. Графиком является прямая, проходящая через начало координат и точку (4; 2).
б) у = –4. Графиком является прямая, проходящая через точку (0; –4) и параллельная оси х.
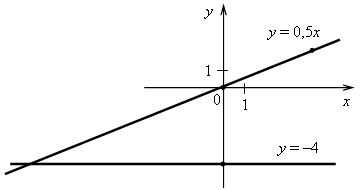
4. (3; –99).
5. у = –5х.
Критерии оценивания:
«5» -если верно выполнены 5 задания;
«4»- если верно выполнены любые 4 задания;
«3» - если верно выполнено любые 3 задания;
«2» - если верно выполнено меньше 3 заданий.
| Контрольная работа №4 Тема: Степень с натуральным показателем 1 вариант | Контрольная работа №4 Тема: Степень с натуральным показателем 2 вариант |
| 1.Вычислите: а) -102∙0,2 б) (-1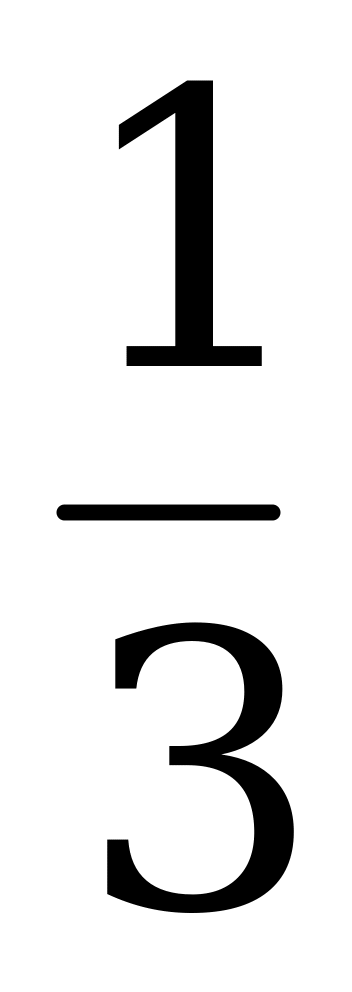 )3 в) 17-(-1)7 )3 в) 17-(-1)7 2.Выполните действия: а) х4∙х б) у6:у2 в) (-2с6)4 г) 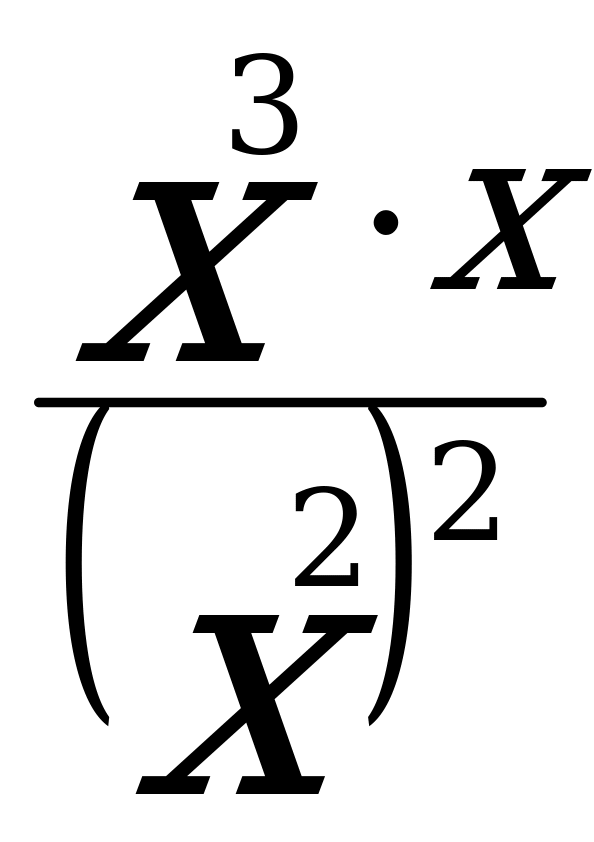 д) (m3∙m4)2∙(2m)3 д) (m3∙m4)2∙(2m)3 3. Решите уравнение  4. Упростите выражение: а) 2а5b2∙ba3 б) (-0,1х3)4∙10х в) (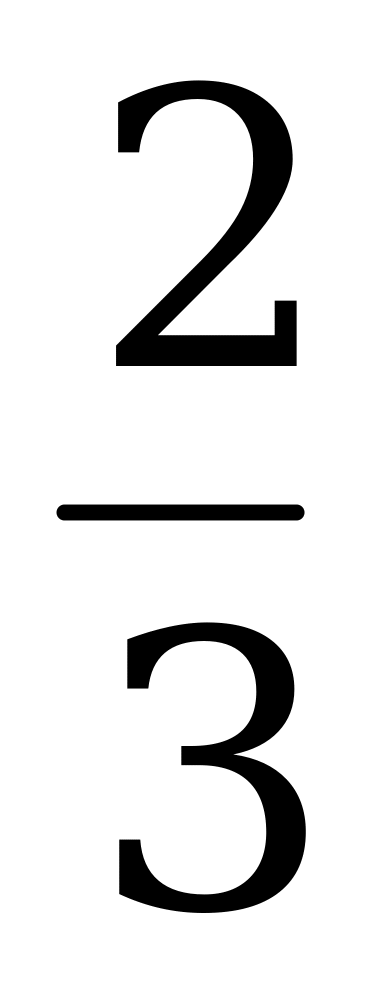 ab2)3∙ ab2)3∙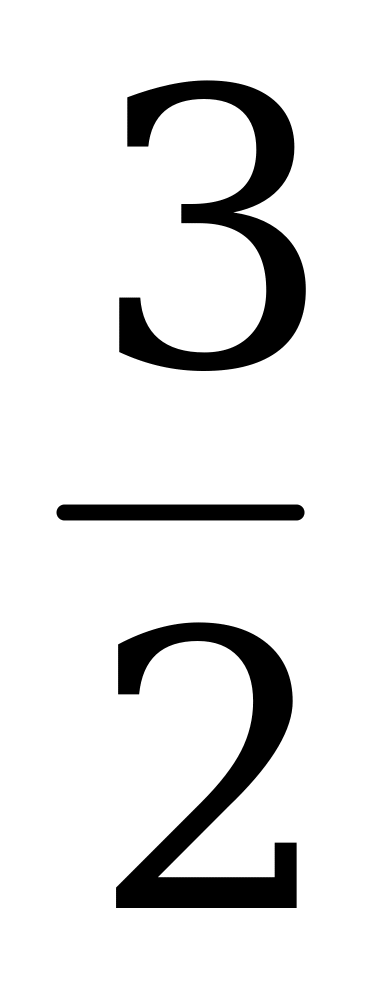 a3b2 a3b2 5. Используя свойства степени, найдите значение выражения: а) 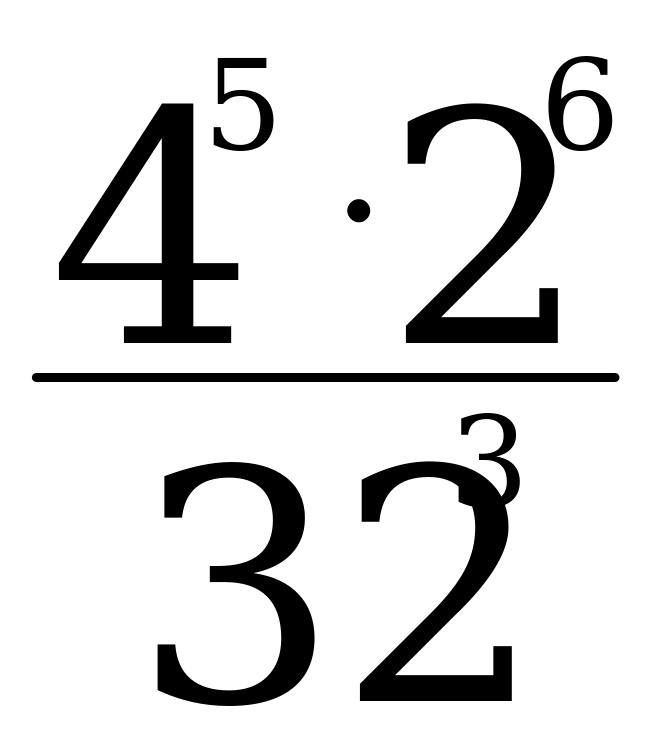 б) б) 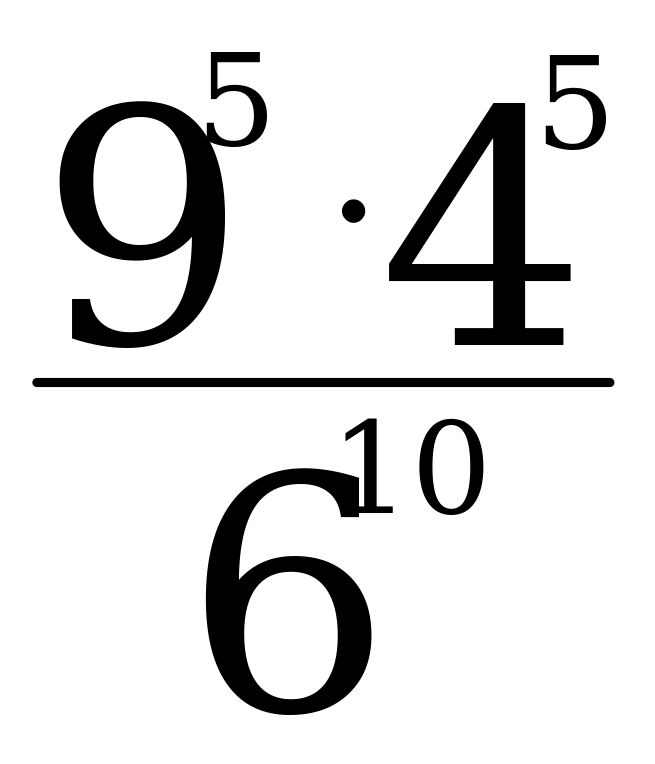  | 1.Вычислите: а) -24∙0,5 б) (-2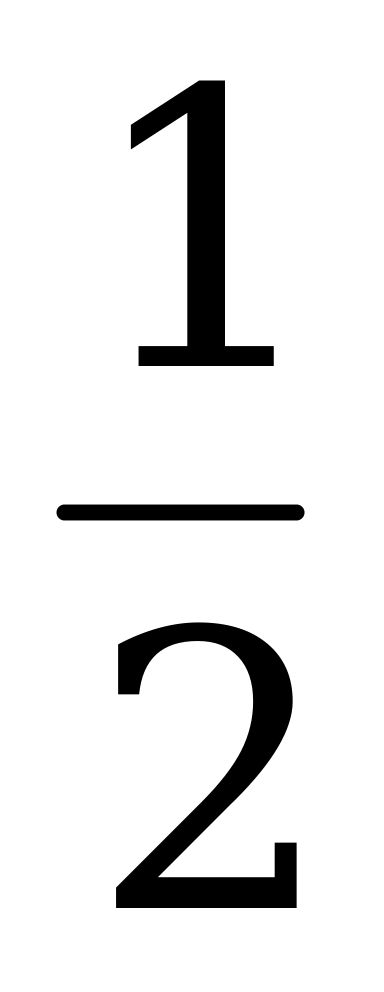 )2 в) (-1)9-19 )2 в) (-1)9-19 2.Выполните действия: а) х3∙х7 б) у4:у в) (-3с4)2 г) 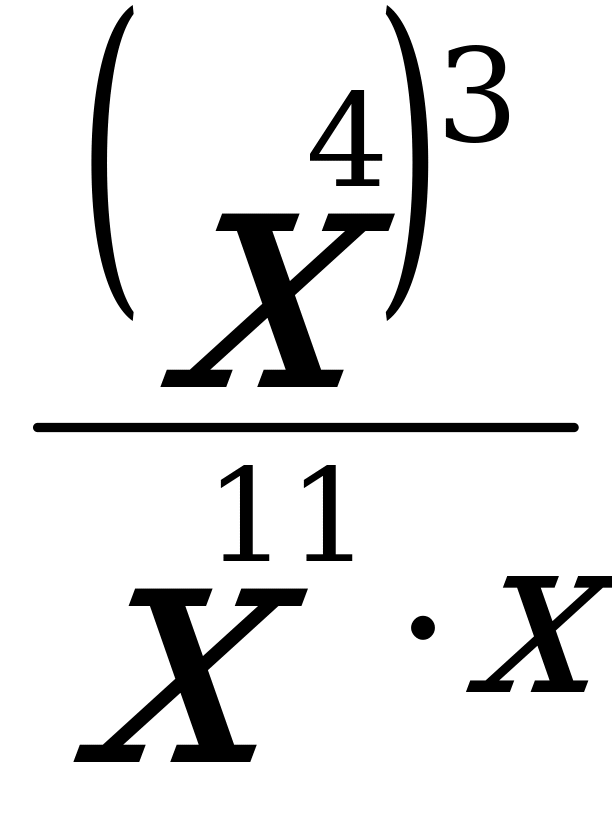 д) (6х)2∙(х∙х5)4 д) (6х)2∙(х∙х5)4 3. Решите уравнение  4. Упростите выражение: а) 3а2b∙b4 a4 б) (-0,2х2)3∙5х2 в) (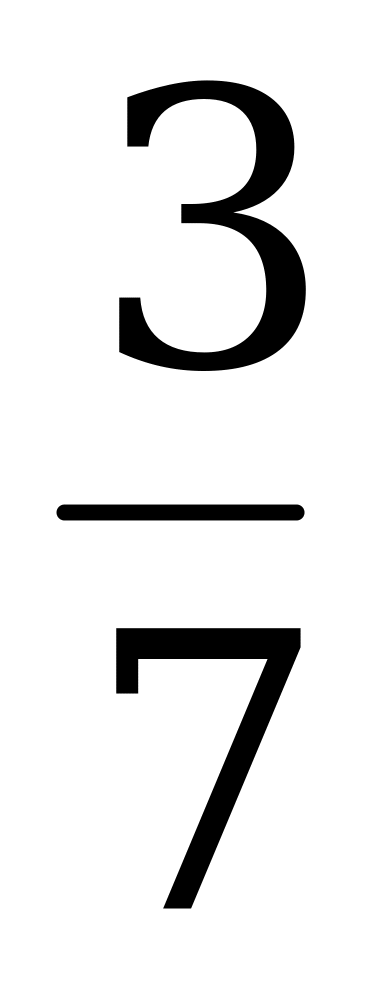 a2 b)2∙ a2 b)2∙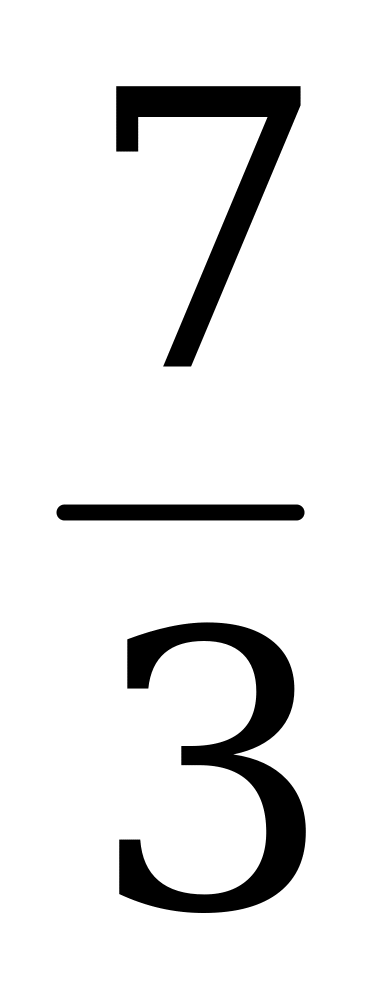 b2а b2а 5. Используя свойства степени, найдите значение выражения: а) 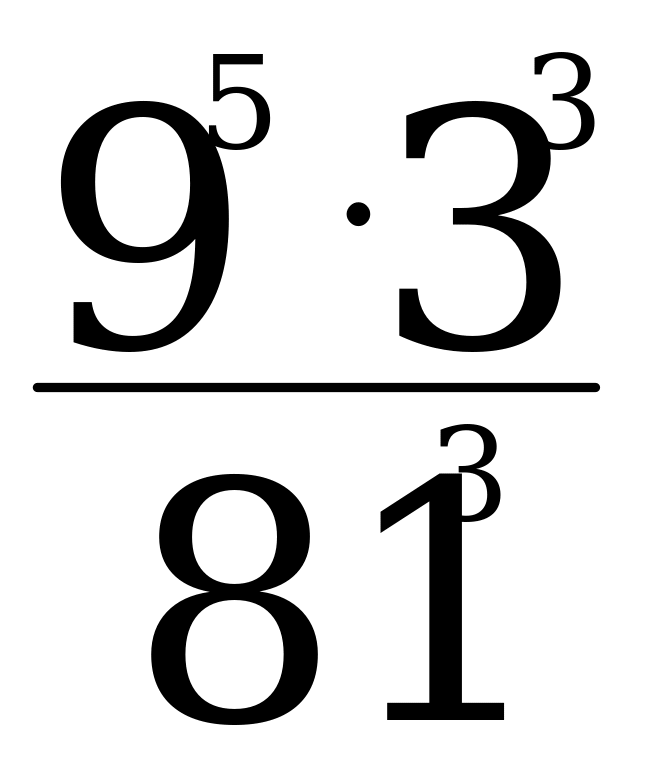 б) б) 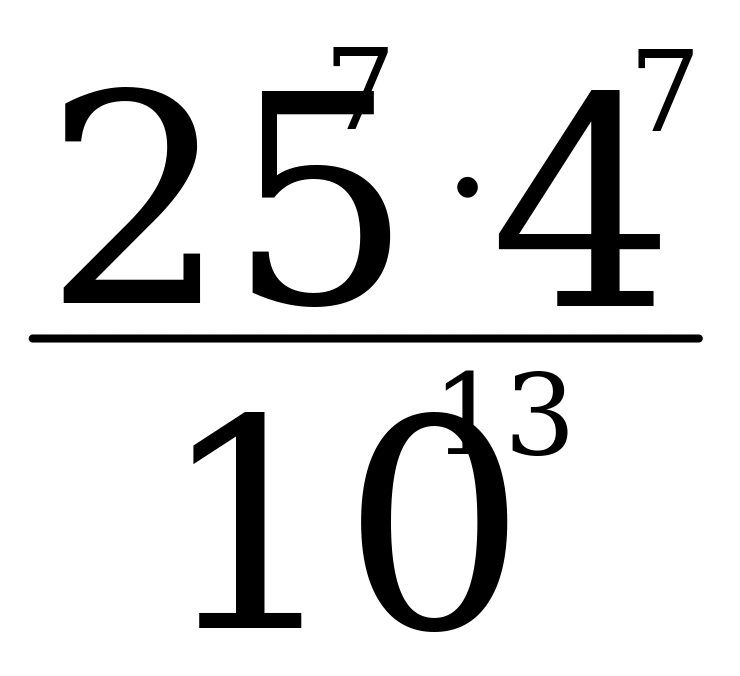  |
|
Контрольная работа №5 Тема. Сложение и вычитание многочленов Вариант 1 Приведите подобные слагаемые: а) �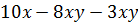 �; �; б) �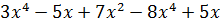 �. �. Раскройте скобки: а) �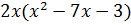 �; �; б) �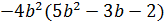 �. �. Решите уравнение: а) � �; �; б) �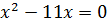 �. �. Разложите на множители: а) �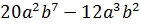 �; �; б) �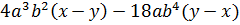 �. �. Упростите выражение 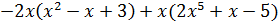 и найдите его значение при �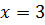 �. �. |
Контрольная работа №5 Тема. Сложение и вычитание многочленов Вариант 2 Приведите подобные слагаемые: а) �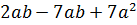 �; �; б)�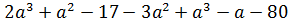 �. �. Раскройте скобки: а) �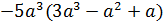 �; �; б) �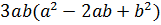 �. �. Решите уравнение: а) �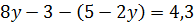 �; �; б) �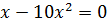 �. �. Разложите на множители: а) �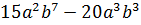 �; �; б) �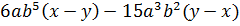 �. �. Упростите выражение 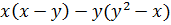 и найдите его значение при � и найдите его значение при �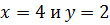 �. �. |
Ответы
Вариант 1
а) �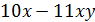 �; б) �
�; б) �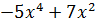 �.
�.
а) �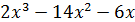 �; б) �
�; б) �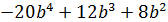 �.
�.
а)-��1,5; б) �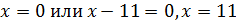 �.
�.
а) �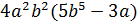 �; б) �
�; б) �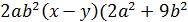 �).
�).
�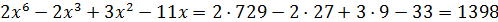 �.
�.
Вариант 2
а) �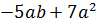 �; б) �
�; б) �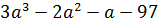 �.
�.
а) �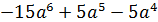 �; б) �
�; б) �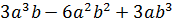 �.
�.
а)�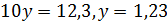 �; б) �
�; б) �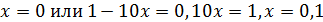 �.
�.
а) �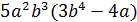 �; б) �
�; б) �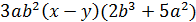 �.
�.
�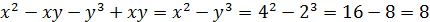 �.
�.
Критерии оценивания:
«5» -если верно выполнены 5 задания;
«4»- если верно выполнены любые 4 задания;
«3» - если верно выполнено любые 3 задания;
«2» - если верно выполнено меньше 3 заданий.
Контрольная работа №6 «Произведение многочленов»
Вариант 1
1. Выполните умножение:
а) (с + 2) (с - 3); б) (2а - 1) (За + 4); в) (5х - 2у) (4х - у); г) (а - 2) (а2 - 3а + 6).
2. Разложите на множители: а) а (а + 3) - 2 (а + 3); б) ах- ау + 5х - 5у.
3. Упростите выражение -0,1x (2х2 + 6) (5 - 4х2).
4. Представьте многочлен в виде произведения:
а) х2 - ху- 4х + 4у; б) ab - ас - bх + сх + с - 6.
5. Из прямоугольного листа фанеры вырезали квадратную пластинку, для чего с одной стороны листа фанеры отрезали полосу шириной 2 см, а с другой, соседней, - 3 см. Найдите сторону получившегося квадрата, если известно, что его площадь на 51 см2 меньше площади прямоугольника.
Вариант 2
1. Выполните умножение:
а) (а - 5) (а - 3); б) (5х + 4) (2х - 1); в) (3р + 2с) (2р + 4с); г) (6 - 2) (b2+ 2b - 3).
2. Разложите на множители: а) х (х - у) + а (х - у);б) 2а - 2b + са - сb.
3. Упростите выражение 0,5х (4х2 - 1) (5х2 + 2).
4. Представьте многочлен в виде произведения:
а) 2а - ас - 2с + с2; 6) bx + by - х - у - ах - ау.
5. Бассейн имеет прямоугольную форму. Одна из его сторон на 6 м больше другой. Он окружен дорожкой, ширина которой 0,5 м. Найдите стороны бассейна, если площадь окружающей его дорожки 15 м2.
Вариант 1: 1. а) с²-с–6 б) 6а²+5а–4 в) 20х²-13ху+2у² г) a³-5a²+12a–12; 2.a) (a+3) (a-2) б) (x-y)(a 5); 3.0.8x⁵+1.4x³-3x; 4.а) (х-4)(х*у) б)(b-c)(a-x-1); 5. 9.
Вариант 2: 1. а) a2-8a+15 б) 10x2-3x+4 в) 6p2+16pc+8c2 г) b3-7b+6; 2. а) (х-у)*(x+a) б) (a-b)*(2+c); 3. 10x5-1,5x3-x. 4. а) (2 - c)(a - c) б) (x + y)(b - a - 1) 5. 4м ширина 10м длина
Критерии оценивания
Задание 1,2
| Безошибочное выполнение (допущен один недочет) | Допущена 1 ошибка | Допущено 2 и более ошибок |
| 2 балла | 1 балл | 0 баллов |
Задание 3,4
| Безошибочное выполнение | Допущена (вычислительная) ошибка | Допущено 2 и более ошибок |
| 3 балла | 2 балла | 0 баллов |
Задание 5
| Безошибочное выполнение | Допущена (вычислительная) ошибка | Допущено 2 и более ошибок |
| 4 балла | 3 балла | 0 баллов |
| Первичный балл | 13-14 | 8-12 | 4-7 | 1-3 | 0 |
| Уровень | высокий | повышенный | базовый | пониженный | низкий |
| Отметка | 5 | 4 | 3 | 2 | 2 |
Контрольная работа № 7
Тема. Формулы сокращенного умножения.
Вариант 1.
1.Представьте в виде многочлена выражение:
а) (c - 6)2; в) (5 – a)(5 + a);
б) (2a – 3b)2; г) (7x + 10y) (10y – 7х).
2.Разложите на множители:
а) b2 – 49; в) 100 – 9x2;
б) c2 – 8c + 16; г) 4a2 + 20ab + 25b2.
3.Упростите выражение (x – 2)(x + 2) – (x – 5)2.
4.Решите уравнение: 4(3y + 1)2 – 27 = (4y + 9) (4y - 9) + 2(5y + 2)(2y – 7)
5.Упростите выражение (3 – b)(3 + b)(9 + b2) + (4 + b2)2 и найдите его значение при b = � �.
�.
6.Докажите, что выражение x2 – 14x + 51 принимает положительные значения при всех значениях x.
Вариант 2.
1.Представьте в виде многочлена выражение:
а) (а + 7)2; в) (m – 6)(m + 6);
б) (3х – 4у)2; г) (5a + 8b) (8b – 5а).
2.Разложите на множители:
а) а2 – 49; в) 25x2 – 16;
б) b2 + 10b + 25; г) 9x2 – 12xy + 4y2.
3.Упростите выражение (x – 1)2 - (x + 3)(x - 3).
4.Решите уравнение: (2y - 3)(3y + 1) + 2(y - 5)(y + 5) = 2(1 – 2y)2 + 6y
5.Упростите выражение (a – 1)(a + 1)(1 + a2) - (9 + a2)2 и найдите его значение при b = �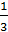 �.
�.
6.Докажите, что выражение x2 – 4x + 5 принимает положительные значения при всех значениях x.
Вариант 1: 1.а) с² – 12с + 36 б) 4а² – 12аb + 9b² в) 25 – а² г) 100у² – 49х²; 2.а) (b – 7) (b + 7) б) (c – 4)² в) (10 – 3x) (10 + 3x) г) (2a + 5b)²; 3.10х – 29; 4. - 1 ;5. 99; 6. (х – 4)² + 2 0 при всех х
Вариант 2: 1.а) а² + 14а + 49 б) 9х² – 24ху + 16у² в) m² – 36 г) 64b² – 25a²; 2.а) (а – 3) (а + 3) б) (b + 5)² в) (5x – 4) (5x + 4) г) (3x – 2y)²; 3. - 2х + 10; 4. – 11; 5. – 84; 6. (х – 2)² + 1 0 при всех х
Критерии оценивания:
«5» -если верно выполнены 6 задания;
«4»- если верно выполнены любые 4-5 задания;
«3» - если верно выполнено любые 3 задания
«2» - если верно выполнено меньше 3 заданий.
Контрольная работа 8
"Преобразование целого выражения в многочлен".
ВАРИАНТ 1
1. Преобразуйте в многочлен:
а) (а – 2)( а + 2) – 2а(5 – а)
б) (у – 9)2 – 3у(у + 1)
в) 3(х – 4) 2 – 3х2
2. Разложите на множители:
а) 25х – х3=x(25-x2)
б) 2х2 – 20х + 50
3. Найдите значение выражения
а2 – 4bс, если а = 6, b = -11, с = -10
4. Упростите выражение:
(с2 – b)2 – (с2 - 1)(с2 + 1) + 2bс2
5. Докажите тождество:
(а + b)2 – (а – b)2 = 4аb
ВАРИАНТ 2
1. Преобразуйте в многочлен:
а) 4х(2х – 1) – (х – 3)(х + 3)
б) (х + 3)(х – 11) + (х + 6)2
в) 7(а + b) 2 – 14аb
2. Разложите на множители:
а) у3 - 49у
б) -3а2 – 6аb - 3b2
3. Найдите значение выражения
а2 – 4bс, если а = 6, b = -7, с = -25
4. Упростите выражение:
(а - 1)2 (а + 1) + (а + 1)( а - 1)
5. Докажите тождество:
(х - у)2 + (х + у)2 = 2(х2 + у2)
Вариант 1: 1. а) 3а2 – 10а – 4; б) -2у2 – 21у + 81; в) – 24х + 48; 2. а) х(5 – х)(5 + х); б) 2(х – 5)2; 3. -404; 4. а) b2 + 1; 5. a2 + 2ab + b2 - a2 + 2ab - b2 .
Вариант 2: 1.а) 7х²-4х+9 б) 2х²-11х+3 в) 7a²-7b²; 2.а) y(y-7)(y+7); б) 3(a+b)²; 3. -664; 4.а³-1; 5.2(х²+у²)=2(х²+у²)
Критерии оценивания:
«5» -если верно выполнены 5 задания;
«4»- если верно выполнены любые 4 задания;
«3» - если верно выполнено любые 3 задания
«2» - если верно выполнено меньше 3 заданий.
Контрольная работа №9
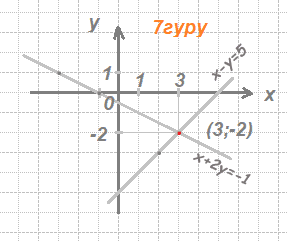
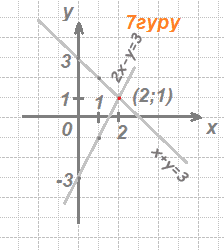
 Вариант 1: 1. (2;-2); 2. (–9; 9,4); 3. (3; - 2); 4. 6 км/ч, 4 км/ч ;5. 1) (2; 1);2) нет решений; 6.- 8
Вариант 1: 1. (2;-2); 2. (–9; 9,4); 3. (3; - 2); 4. 6 км/ч, 4 км/ч ;5. 1) (2; 1);2) нет решений; 6.- 8
Вариант 2: 1. (2; - 2); 2. (20; –9); 3. (2; 1); 4. 14 км/ч, 12 км/ч; 5. 1) (3; 2); 2) нет решений 6. 1
Критерии оценивания:
«5» -если верно выполнены 5-6 задания;
«4»- если верно выполнены любые 4 задания;
«3» - если верно выполнено любые 3 задания
«2» - если верно выполнено меньше 3 заданий.
Итоговая контрольная работа

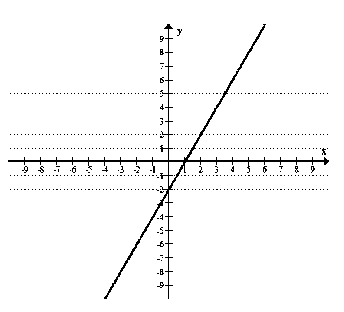
Вариант 1: 1. 5а2 + 6а + 36; 2. х = –1; y = –8; 3.а) рис. б) –20 ≠ –22. Неверно, график функции не проходит через А(–10; –20); 4.а) 2a2b2(a2b – ab2 + 3); б) (х + у)(x – у – 3); 5. 14 км/ч
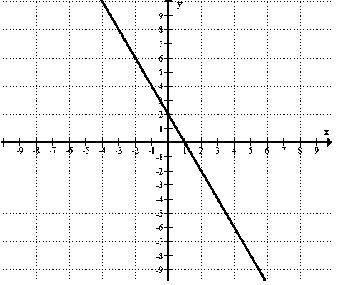
Вариант 2: 1. –5x + 6; 2. у = 3; x = –1; 3.а) рис. б) – 2 • 10 + 2 = –18; –18 = –18. Верно, график функции проходит через А (10;–18). 4.а) 3ху2(х2у + ху2 – 2); б) (а – b) (а + b + 2); 5. 12 км/ч и 40 км/ч.
Критерии оценивания:
«5» -если верно выполнены 5 задания;
«4»- если верно выполнены любые 4 задания;
«3» - если верно выполнено любые 3 задания
«2» - если верно выполнено меньше 3 заданий.
2













 Вариант 1: 1. (2;-2); 2. (–9; 9,4); 3. (3; - 2); 4. 6 км/ч, 4 км/ч ;5. 1) (2; 1);2) нет решений; 6.- 8
Вариант 1: 1. (2;-2); 2. (–9; 9,4); 3. (3; - 2); 4. 6 км/ч, 4 км/ч ;5. 1) (2; 1);2) нет решений; 6.- 8














