I.Пояснительная записка
Рабочая программа по алгебре для 9 класса составлена на основе федерального государственного образовательного стандарта основного общего образования, основной образовательной программы основного общего образования МБОУ СОШ №3, учебного плана МБОУ СОШ №3, примерной программы основного общего образования по математике //Примерные программы по учебным предметам. Математика. 5-9 классы.- М. Просвещение, 2011.с учетом авторской программы по алгебре С.М. Никольского входящей в сборник рабочих программ «Программы общеобразовательных учреждений: Алгебра, 7-9 классы», составитель: Т.А. Бурмистрова «Программы общеобразовательных учреждений: Алгебра , 7-9 классы».- М. Просвещение, 2011.
Рабочая программа ориентирована на использование учебника: «Алгебра». 9 класс: учеб. для общеобразоват. организаций / С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин. – 2-е изд. – М: Просвещение, 2016.
Программа рассчитана на 102 часа из расчета 3 учебных часа в неделю. В ходе реализации данной рабочей программы предусмотрено:
контрольных работ -10;
практических работ – 3;
проектных работ – 2.
II. Планируемые результаты освоения предмета «Алгебра».
В результате изучения курса алгебры в основной школе должны быть достигнуты определённые результаты (личностные, метапредметные и предметные).
Личностные;
умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
представление о математической науке как сфере человеческой деятельности, об этапах ее развития, о ее значимости для развития цивилизации;
креативность мышления, инициатива, находчивость, активность при решении математических задач;
умение контролировать процесс и результат учебной математической деятельности;
способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений;
метапредметные:
первоначальные представления об идеях и о методах математики как универсальном языке науки и техники, средстве моделирования явлений и процессов;
умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
умение находить в различных источниках информацию, необходимую для решения математических проблем, представлять ее в понятной форме, принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
умение понимать и использовать математические средства наглядности (графики, диаграммы, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;
умение выдвигать гипотезы при решении учебных задач, понимать необходимость их проверки;
умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задачи;
понимать сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;
предметные:
овладение базовым понятийным аппаратом по основным разделам содержания, представление об основных изучаемых понятиях (число, геометрическая фигура, уравнение, функция, вероятность) как важнейших математических моделях, позволяющих описывать и изучать реальные процессы и явления;
умение работать с математическим текстом (анализировать, извлекать необходимую информацию), грамотно применять математическую терминологию и символику, использовать различные языки математики;
умение проводить классификации, логические обоснования, доказательства математических утверждений;
умение распознавать виды математических утверждений (аксиомы, теоремы и др.), прямые и обратные теоремы;
развитие представлений о числе и числовых системах от натуральных до действительных чисел, овладение навыками устных, письменных, инструментальных вычислений;
овладение символическим языком алгебры, приемами выполнения тождественных преобразований рациональных выражений, решения уравнений, систем уравнений, неравенств и систем неравенств, умение использовать идею координат на плоскости для интерпретации уравнений, неравенств, систем, умение применять алгебраические преобразования, аппарат уравнений и неравенств для решения задач из различных разделов курса;
овладение системой функциональных понятий, функциональным языком и символикой, умение на основе функционально-графических представлений описывать и анализировать реальные зависимости;
овладение основными способами представления и анализа статистических данных; наличие представлений о статистических закономерностях в реальном мире и о различных способах их изучения, о вероятностных моделях;
овладение геометрическим языком, умение использовать его для описания предметов окружающего мира, развитие пространственных представлений и изобразительных умений, приобретение навыков геометрических построений;
усвоение систематических знаний о плоских фигурах и их свойствах, а также на наглядном уровне – о простейших пространственных телах, умение применять систематические знания о них для решения геометрических и практических задач;
умения измерять длины отрезков, величины углов, использовать формулы для нахождения периметров, площадей и объемов геометрических фигур;
умения применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости справочных материалов, калькулятора, компьютера.
III. Содержание учебного предмета «Алгебра»
9 класс
Содержание курса обучения
1. Линейные неравенства с одним неизвестным (8 часов).
Неравенства первой степени с одним неизвестным. Линейные неравенства с одним неизвестным. Системы линейных неравенств с одним неизвестным.
Основная цель — выработать умение решать неравенства первой степени с одним неизвестным, линейные неравенства и системы линейных неравенств.В данной теме вводится понятие неравенства первой степени с одним неизвестным (kx + b 0, kx + b , k ≠ 0). Решение таких неравенств основывается на свойствах числовых неравенств и иллюстрируется с помощью графиков линейных функций. Вводятся понятия линейного неравенства, системы линейных неравенств и рассматриваются приемы их решения.
2. Неравенства второй степени с одним неизвестным (11 часов).
Неравенства второй степени с одним неизвестным. Неравенства, сводящиеся к неравенствам второй степени.
Основная цель — выработать умение решать неравенства второй степени с одним неизвестным.
Вводятся понятия неравенства второй степени с одним неизвестным и его дискриминанта D, последовательно рассматриваются случаи D 0, D =0, D 0. Решение неравенств основано на определении знака квадратного трехчлена на интервалах и иллюстрируется схематическим построением графиков квадратичных функций.
3. Рациональные неравенства (11 часов).
Метод интервалов. Решение рациональных неравенств. Системы рациональных неравенств. Нестрогие рациональные неравенства. Доказательство числовых неравенств.
Основная цель — выработать умение решать рациональные неравенства и их системы, нестрогие неравенства.
При решении рациональных неравенств используется метод интервалов, который, по сути, применялся уже при решении квадратных неравенств. Показывается равносильность неравенств вида 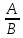 0 и
0 и 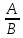 0 неравенствам А·В 0 и А·В соответственно (А и В — многочлены).
0 неравенствам А·В 0 и А·В соответственно (А и В — многочлены).
После изучения строгих неравенств: линейных, квадратных, рациональных — рассматриваются нестрогие неравенства всех ранее изученных типов и их системы.
Решение нестрогих неравенств должно состоять из трех этапов:
1) решить уравнение;
2) решить строгое неравенство;
3) объединить решения уравнения и строгого неравенства.
Попытка отойти от этого правила часто приводит к ошибкам.
4. Функция у = хn (3 часа).
Свойства функции у =- хn и ее график.
Основная цель — изучить свойства функций у = хn графики.
5. Корень степени n (12 часов).
Корень n-й степени. Корни четной и нечетной степени. Арифметический корень. Свойства корней n-й степени. Корень n-й степени из натурального числа. Функция у =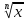 (х ≥ 0). Степень с рациональным показателем и ее свойства.
(х ≥ 0). Степень с рациональным показателем и ее свойства.
Основная цель — изучить свойства функций у =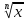 (x ≥ 0) и их графики, свойства корня n-й степени; выработать умение преобразовывать выражения, содержащие корни п-й степени.
(x ≥ 0) и их графики, свойства корня n-й степени; выработать умение преобразовывать выражения, содержащие корни п-й степени.
В данной теме рассматриваются понятие и свойства корня n-й степени. Но от учащихся требуется знание лишь корней второй и третьей степени и их свойств.
5. Числовые последовательности и их свойства (2 часа).
Числовая последовательность. Свойства числовых последовательностей. Арифметическая и геометрическая прогрессии. Формулы суммы п первых членов арифметической и геометрической прогрессий. Бесконечно убывающая геометрическая прогрессия.
Основная цель — выработать умения, связанные с задачами на арифметическую и геометрическую прогрессии.
В данной теме вводятся понятия числовой последовательности, арифметической и геометрической прогрессий, решаются традиционные задачи, связанные с формулами n-го члена и суммы п первых членов арифметической и геометрической прогрессий.
7. Арифметическая прогрессия (7 часов).
Арифметическая прогрессия. Формулы суммы п первых членов арифметической прогрессии. Основная цель — выработать умения, связанные с задачами на арифметическую прогрессию.
8.Геометрическая прогрессия (7 часов).
Геометрическая прогрессия. Формулы суммы п первых членов геометрической прогрессии. Бесконечно убывающая геометрическая прогрессия.
Основная цель — выработать умения, связанные с задачами на геометрическую прогрессию.
В данной теме вводятся понятия числовой последовательности, арифметической и геометрической прогрессий, решаются традиционные задачи, связанные с формулами n-го члена и суммы п первых членов арифметической и геометрической прогрессий.
9. Синус, косинус, тангенс и котангенс угла (11 часов).
Понятие угла. Определение синуса и косинуса угла. Основные формулы для sin а и cos а. Тангенс и котангенс угла. Косинус и синус разности и суммы двух углов. Сумма и разность синусов и косинусов. Формулы для двойных и половинных углов. Произведение синусов и косинусов.
Основная цель — усвоить понятия синуса, косинуса, тангенса и котангенса произвольного угла, выработать умения по значению одной из этих величин находить другие и выполнять тождественные преобразования простейших тригонометрических выражений, усвоить формулы косинуса и синуса суммы и разности двух углов, суммы и разности косинусов и синусов, формулы для двойных и половинных углов; выработать умение выполнять тождественные преобразования тригонометрических выражений с использованием выведенных формул.
Данная тема курса алгебры опирается на определения и некоторые факты из курса геометрии. Все тригонометрические формулы следует привести с доказательством, не используя термины «тригонометрические функции» и «формулы приведения».
10. Приближения чисел (6 часов)
Абсолютная и относительная погрешности приближения. Приближения суммы и разности, произведения и частного двух чисел, суммы нескольких слагаемых. Приближенные вычисления с калькулятором.
Основная цель — усвоить понятия абсолютной и относительной погрешностей приближения, выработать умение выполнять оценку результатов вычислений.
В данной теме вводятся понятия абсолютной и относительной погрешностей приближения, показываются приемы оценки результатов вычислений при сложении, вычитании, умножении, делении.
11. Комбинаторика (5 часов).
Примеры комбинаторных задач, перестановки, размещения.
Основная цель – дать понятия комбинаторики, перестановки, размещения, научить решать связанные с ними задачи.
12. Введение в теорию вероятности (8 часов).
Представление данных в виде таблиц, диаграмм, графиков. Случайная изменчивость. Статистические характеристики набора данных: среднее арифметическое, медиана, наибольшее и наименьшее значения, размах. Представление о выборочном исследовании.
Понятие о случайном опыте и случайном событии. Частота случайного события. Статистический подход к понятию вероятности. Вероятности противоположных событий. Независимые события. Умножение вероятностей. Достоверные и невозможные события. Равно возможность событий. Классическое определение вероятности.
13. Повторение (11 часов).
Можно использовать любой экзаменационный сборник для подготовки учеников к государственной итоговой аттестации.
IV. Планируемые результаты изучения учебного предмета «Алгебра» в 9 классе.
НЕРАВЕНСТВА
Выпускник научится:
1) понимать и применять терминологию и символику, связанные с отношением неравенства, свойства числовых неравенств;
2) решать линейные неравенства с одной переменной и их системы; решать квадратные неравенства с опорой на графические представления;
3) применять аппарат неравенств для решения задач из различных разделов курса.
Выпускник получит возможность научиться:
4) разнообразным приёмам доказательства неравенств; уверенно применять аппарат неравенств для решения разнообразных математических задач и задач из смежных предметов, практики;
5) применять графические представления для исследования неравенств, систем неравенств, содержащих буквенные коэффициенты.
ОСНОВНЫЕ ПОНЯТИЯ. ЧИСЛОВЫЕ ФУНКЦИИ
Выпускник научится:
1) понимать и использовать функциональные понятия и язык (термины, символические обозначения);
2) строить графики элементарных функций; исследовать свойства числовых функций на основе изучения поведения их графиков;
3) понимать функцию как важнейшую математическую модель для описания процессов и явлений окружающего мира, применять функциональный язык для описания и исследования зависимостей между физическими величинами.
Выпускник получит возможность научиться:
4) проводить исследования, связанные с изучением свойств функций, в том числе с использованием компьютера; на основе графиков изученных функций строить более сложные графики (кусочно-заданные, с «выколотыми» точками и т. п.);
5) использовать функциональные представления и свойства функций для решения математических задач из различных разделов курса.
ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
Выпускник научится:
1) понимать и использовать язык последовательностей (термины, символические обозначения);
2) применять формулы, связанные с арифметической и геометрической прогрессиями, и аппарат, сформированный при изучении других разделов курса, к решению задач, в том числе с контекстом из реальной жизни.
Выпускник получит возможность научиться:
3) решать комбинированные задачи с применением формул n-го члена и суммы первых n членов арифметической и геометрической прогрессий, применяя при этом аппарат уравнений и неравенств;
4) понимать арифметическую и геометрическую прогрессии как функции натурального аргумента; связывать арифметическую прогрессию с линейным ростом, геометрическую — с экспоненциальным ростом.
ОПИСАТЕЛЬНАЯ СТАТИСТИКА
Выпускник научится использовать простейшие способы представления и анализа статистических данных.
Выпускник получит возможность приобрести первоначальный опыт организации сбора данных при проведении опроса общественного мнения, осуществлять их анализ, представлять результаты опроса в виде таблицы, диаграммы.
СЛУЧАЙНЫЕ СОБЫТИЯ И ВЕРОЯТНОСТЬ
Выпускник научится находить относительную частоту и вероятность случайного события.
Выпускник получит возможность приобрести опыт проведения случайных экспериментов, в том числе с помощью компьютерного моделирования, интерпретации их результатов.
КОМБИНАТОРИКА
Выпускник научится решать комбинаторные задачи на нахождение числа объектов или комбинаций.
Выпускник получит возможность научиться некоторым специальным приёмам решения комбинаторных задач.
Приложение. Календарно-тематическое планирование по алгебре 9 класс (3 часа)
| № | Дата по плану | Дата по факту | Тема | Элемент содержания
| Количество часов | В том числе |
| Контрольные работы | Лабораторные/ практические работы | Проектные работы |
| Тема 1: Повторение (5 часов) |
| 1. |
|
| Квадратные корни. Рациональные уравнения |
| 1 |
|
|
|
| 2. |
|
| Линейная и квадратичная функции |
| 1 |
|
|
|
| 3. |
|
| Системы рациональных уравнений |
| 1 |
|
|
|
| 4. |
|
| Задачи на составление уравнений и систем уравнений |
| 1 |
|
|
|
| 5. |
|
| Диагностическая контрольная работа | 1 | 1 |
|
|
| Тема 2. Линейные неравенства с одним неизвестным (8 часов) |
| 6. |
|
| Неравенства первой степени с одним неизвестным | Определение неравенства первой степени с одним неизвестным. | 1 |
|
|
|
| 7. |
|
| Неравенства первой степени с одним неизвестным. | Определение неравенства первой степени с одним неизвестным. | 1 |
|
|
|
| 8. |
|
| Применение графиков к решению неравенств первой степени с одним неизвестным | Алгоритм построения графика линейной функции | 1 |
|
|
|
| 9. |
|
| Линейные неравенства с одним неизвестным | Понятие линейного неравенства с одним неизвестным x; члены неравенства | 1 |
|
|
|
| 10. |
|
| Линейные неравенства с одним неизвестным. | Понятие линейного неравенства с одним неизвестным x; члены неравенства | 1 |
|
|
|
| 11. |
|
| Системы линейных неравенств с одним неизвестным | Понятие системы линейных неравенства с одним неизвестным | 1 |
|
|
|
| 12. |
|
| Системы линейных неравенств с одним неизвестным. | Решение систем линейных неравенства с одним неизвестным | 1 |
|
|
|
| 13. |
|
| Системы линейных неравенств с одним неизвестным. | Графическое решение систем линейных неравенства с одним неизвестным | 1 |
|
|
|
| Тема 3. Неравенства второй степени с одним неизвестным (11 часов) |
| 14. |
|
| Понятие неравенства второй степени с одним неизвестным | Понятие неравенства второй степени с одним неизвестным | 1 |
|
|
|
| 15. |
|
| Понятие неравенства второй степени с одним неизвестным | Примеры неравенств с двумя переменными. | 1 |
|
|
|
| 16. |
|
| Неравенства второй степени с положительным дискриминантом | Алгоритм решения неравенства второй степени с положительным дискриминантом | 1 |
|
|
|
| 17. |
|
| Неравенства с положительным дискриминантом. | Алгоритм решения неравенства второй степени с положительным дискриминантом | 1 |
|
|
|
| 18. |
|
| Неравенства второй степени с положительным дискриминантом | Алгоритм решения неравенства второй степени с положительным дискриминантом | 1 |
|
|
|
| 19. |
|
| Неравенства второй степени с дискриминантом, равным нулю | Алгоритм решения неравенства второй степени с дискриминантом, равным нулю | 1 |
|
|
|
| 20. |
|
| Неравенства 2-й степени с дискриминантом, равным нулю. | Алгоритм решения неравенства второй степени с дискриминантом, равным нулю | 1 |
|
|
|
| 21. |
|
| Неравенства второй степени с отрицательным дискриминантом | Алгоритм решения неравенства второй степени с отрицательным дискриминантом | 1 |
|
|
|
| 22. |
|
| Неравенства второй степени с отрицательным дискриминантом. | Алгоритм решения неравенства второй степени с отрицательным дискриминантом | 1 |
|
|
|
| 23. |
|
| Неравенства, сводящиеся к неравенствам второй степени | Алгоритмы решения неравенства второй степени | 1 |
|
|
|
| 24. |
|
| Контрольная работа №1 по теме «Неравенства» | 1 | 1 |
|
|
| Тема 4. Рациональные неравенства (11 часов) |
| 25. |
|
| Метод интервалов | Алгоритм решения неравенств методом интервалов | 1 |
|
|
|
| 26. |
|
| Метод интервалов. | Алгоритм решения неравенств методом интервалов | 1 |
|
|
|
| 27. |
|
| Решение рациональных неравенств | Алгоритм решения неравенств методом интервалов | 1 |
|
|
|
| 28. |
|
| Решение рациональных неравенств | Алгоритм решения неравенств методом интервалов | 1 |
|
|
|
| 29. |
|
| Решение рациональных неравенств | Алгоритм решения неравенств методом интервалов | 1 |
|
|
|
| 30. |
|
| Системы рациональных неравенств | Понятие системы рациональных неравенств | 1 |
|
|
|
| 31. |
|
| Системы рациональных неравенств. | Понятие системы рациональных неравенств | 1 |
|
|
|
| 32. |
|
| Нестрогие рациональные неравенства | Понятие нестрогих рациональных неравенств и этапы их решения | 1 |
|
|
|
| 33. |
|
| Нестрогие рациональные неравенства | Понятие нестрогих рациональных неравенств и этапы их решения | 1 |
|
|
|
| 34. |
|
| Нестрогие рациональные неравенства. | Понятие нестрогих рациональных неравенств и этапы их решения | 1 |
|
|
|
| 35. |
|
| Контрольная работа №2 по теме «Рациональные неравенства» | 1 | 1 |
|
|
| Тема 5. Корень степени n (15 часов) |
| 36. |
|
| Свойства функции y = xn | Свойства функции y=x | 1 |
|
|
|
| 37. |
|
| Свойства функции y = xn | Свойства функции y=x | 1 |
|
|
|
| 38. |
|
| График функции y = xn | График функции y = xn Построение график а функции по результатам ее исследования | 1 |
|
|
|
| 39. |
|
| График функции y = xn | График функции y = xn Построение график а функции по результатам ее исследования | 1 |
| 1 |
|
| 40. |
|
| Понятие корня степени n | Понятие корня степени n | 1 |
|
|
|
| 41. |
|
| Понятие корня степени n | Понятие корня степени n | 1 |
|
|
|
| 42. |
|
| Корни четной и нечетной степеней | Понятие корня чётной и нечётной степени n | 1 |
|
|
|
| 43. |
|
| Корни четной и нечетной степеней | Понятие корня чётной и нечётной степени n | 1 |
|
|
|
| 44. |
|
| Арифметический корень | Определение арифметического корня | 1 |
|
|
|
| 45. |
|
| Арифметический корень | Определение арифметического корня | 1 |
|
|
|
| 46. |
|
| Свойства корней степени n | Формулы свойств коня степени n | 1 |
|
|
|
| 47. |
|
| Свойства корней степени n | Формулы свойств коня степени n | 1 |
|
|
|
| 48. |
|
| Корень степени n из натурального числа | Упражнения на применение свойств коня степени n | 1 |
|
|
|
| 49. |
|
| Корень степени n из натурального числа | Упражнения на применение свойств коня степени n | 1 |
|
|
|
| 50. |
|
| Контрольная работа №3 по теме «Корень степени n» | 1 | 1 |
|
|
| Тема 6. Числовые последовательности и их свойства (2 часа) |
| 51. |
|
| Понятие числовой последовательности | Ввести понятие числовой последовательности, способы задания последовательностей, применять полученные знания на практике. | 1 |
|
|
|
| 52. |
|
| Понятие числовой последовательности | Работать над заданием числовых последовательностей, определять свойства последовательностей | 1 |
|
|
|
| Тема 7. Арифметическая прогрессия (7 часов) |
| 53. |
|
| Понятие арифметической прогрессии | Ввести понятие арифметической прогрессии, виды прогрессий. | 1 |
|
|
|
| 54. |
|
| Понятие арифметической прогрессии | Применение полученных знаний для выделения арифметической прогрессии. | 1 |
|
|
|
| 55. |
|
| Понятие арифметической прогрессии | Ввести формулу n – ого члена арифметической прогрессии, применять формулу для нахождения n – ого члена, разности и первого члена прогрессии | 1 |
|
|
|
| 56. |
|
| Сумма n первых членов арифметической прогрессии | Ввести формулу суммы n членов арифметической прогрессии и применять ее для нахождения суммы. | 1 |
|
|
|
| 57. |
|
| Сумма n первых членов арифметической прогрессии | Применять формулу суммы n членов арифметической прогрессии и вывести характеристическое свойство арифметической прогрессии. | 1 |
|
|
|
| 58. |
|
| Сумма n первых членов арифметической прогрессии | Применять формулы для нахождения n – ого члена, разности и первого члена прогрессии, суммы n членов арифметической прогрессии и характеристического свойства арифметической прогрессией | 1 |
|
|
|
| 59. |
|
| Контрольная работа №4 по теме «Арифметическая прогрессия» | 1 | 1 |
|
|
| Тема 8. Геометрическая прогрессия (7 часов) |
| 60. |
|
| Понятие геометрической прогрессии | Ввести понятие геометрической прогрессии, вывести формулы n – ого члена и суммы n членов геометрической прогрессии по аналогии с арифметической. | 1 |
|
|
|
| 61. |
|
| Понятие геометрической прогрессии | Применять формулы n – ого члена и суммы n членов геометрической прогрессии для нахождения n – ого члена и суммы n членов. | 1 |
|
|
|
| 62. |
|
| Понятие геометрической прогрессии | Применять формулы n – ого члена и суммы n членов геометрической прогрессии для нахождения n – ого члена и суммы n членов. | 1 |
|
|
|
| 63. |
|
| Сумма n первых членов геометрической прогрессии | Применять формулы n – ого члена и суммы n членов геометрической прогрессии для нахождения частного и первого члена прогрессии. | 1 |
|
|
|
| 64. |
|
| Сумма n первых членов геометрической прогрессии | Применять формулы n – ого члена и суммы n членов геометрической прогрессии. Ввести характеристическое свойство геометрической прогрессией, применять его на практике. | 1 |
|
|
|
| 65. |
|
| Сумма n первых членов геометрической прогрессии | Применять характеристические свойства арифметической и геометрической прогрессий для решения нестандартных задач. | 1 |
| 1 |
|
| 66. |
|
| Контрольная работа №5 по теме «Геометрическая прогрессия» | 1 | 1 |
|
|
| Тема 9. Синус, косинус, тангенс и котангенс угла (11 часов) |
| 67. |
|
| Понятие угла | Ввести определение единичной окружности, координаты точки , ввести алгоритм определения координат точки на координатной окружности. | 1 |
|
|
|
| 68. |
|
| Градусная мера угла | Градус. Определять координаты точки на координатной окружности | 1 |
|
|
|
| 69. |
|
| Градусная мера угла | Градус. Определять координаты точки на координатной окружности | 1 |
|
|
|
| 70. |
|
| Радианная мера угла | Радиан. Перевод из градусной меры угла в радианную. | 1 |
|
|
|
| 71. |
|
| Радианная мера угла | Радиан. Перевод из градусной меры угла в радианную. | 1 |
|
|
|
| 72. |
|
| Определение синуса и косинуса угла. | Ввести определение синуса, косинуса полного угла; применять определение для углов окружности. | 1 |
|
|
|
| 73. |
|
| Определение синуса и косинуса угла. | Основные тригонометрические тождества для определения значений тригонометрических величин по известному значению одной из них | 1 |
|
|
|
| 74. |
|
| Основные формулы для синуса и косинуса угла. | Формулы приведения для нахождения значений тупых углов и углов больше 1800. | 1 |
|
|
|
| 75. |
|
| Основные формулы для синуса и косинуса угла. | Ввести формулы связи тригонометрических величин одного угла. | 1 |
|
|
|
| 76. |
|
| Тангенс и котангенс угла. | Ввести определение синуса, косинуса, тангенса и котангенса полного угла. | 1 |
|
| 1 |
| 77. |
|
| Контрольная работа №6 по теме «Синус, косинус, тангенс и котангенс угла» | 1 | 1 |
|
|
| Тема 10. Приближения чисел (6 часов) |
| 78. |
|
| Абсолютная погрешность приближения. | Определение абсолютной погрешности | 1 |
|
|
|
| 79. |
|
| Относительная погрешность приближения. | Определение Относительной погрешности | 1 |
|
|
|
| 80. |
|
| Приближение суммы и разности | Формула приближения суммы и разности | 1 |
|
|
|
| 81. |
|
| Приближение произведения и частного. | Формула приближения суммы и разности | 1 |
|
|
|
| 82. |
|
| Способы представление числовых данных. | Представление различных способов по представлению данных | 1 |
|
|
|
| 83. |
|
| Характеристика числовых данных. | Статистические характеристики данных | 1 |
|
|
|
| Тема 11. Комбинаторика (5 часов). |
| 84. |
|
| Задачи на перебор всех возможных вариантов. | Решение комбинаторных задач геометрического содержания; применение правила произведения и метода граф. | 1 |
|
|
|
| 85. |
|
| Комбинаторное правило | Различные комбинаторные задачи. | 1 |
|
|
|
| 86. |
|
| Перестановки | Различные комбинаторные задачи. | 1 |
|
|
|
| 87. |
|
| Размещение | Различные комбинаторные задачи. | 1 |
|
| 1 |
| 88. |
|
| Сочетание | Различные комбинаторные задачи. | 1 |
|
|
|
| Тема 12. Теория вероятности (8 часов) |
| 89. |
|
| Случайные события |
| 1 |
|
|
|
| 90. |
|
| Случайные события |
| 1 |
|
|
|
| 91. |
|
| Вероятность случайных событий | Определение вероятности. Равновозможные события. | 1 |
|
|
|
| 92. |
|
| Вероятность случайных событий | Подсчет вероятности событий. Представление о геометрической вероятности. | 1 |
|
|
|
| 93. |
|
| Сумма, произведение и разность случайных событий | Применение классического определения случайного события, принцип произведения. | 1 |
|
|
|
| 94. |
|
| Несовместимые события | Ввести понятия «алгебра событий»; определение: объединение, пересечение событий и их разности. Закрепить понятия невозможных и достаточных события, противоположного события при выполнении практических задач. | 1 |
| 1 |
|
| 95. |
|
| Частота случайных событий | Ввести понятия: частота событий. | 1 |
|
|
|
| 96. |
|
| Контрольная работа №7 по теме «Комбинаторика и теория вероятности» | 1 | 1 |
|
|
| Тема 13. Повторение (6 часов) |
| 97. |
|
| Функции. Свойства и графики | Функция, её аргумент, значение функции. Область определения и область значения функции. | 1 |
|
|
|
| 98. |
|
| Функции. Свойства и графики | Примеры функций, заданных описанием, таблицей, графиком, формулой. | 1 |
|
|
|
| 99. |
|
| Решение текстовых задач. | Текстовые задачи различного характера, в том числе с геометрическим содержанием. | 1 |
|
|
|
| 100. |
|
| Решение текстовых задач. | Текстовые задачи с различным содержанием, решаемые с помощью составления систем уравнений. | 1 |
|
|
|
| 101. |
|
| Итоговая контрольная работа | КИМ в формате ОГЭ | 1 | 1 |
|
|
| 102. |
|
| Промежуточная контрольная работа | КИМ в формате ОГЭ | 1 | 1 |
|
|
| Итого 102 часа. | 102 часа | 10 | 3 | 2 |
ПРИЛОЖЕНИЕ 1. Критерии и нормы оценивания результатов
учебной деятельности обучающихся
1. В основу критериев оценивания результатов учебной деятельности обучающихся положен компетентностный подход.
Оценка "5" ставится в случае:
Знания, понимания, глубины усвоения обучающимся всего объёма программного материала.
Умения выделять главные положения в изученном материале, на основании фактов и примеров обобщать, делать выводы, устанавливать межпредметные и внутрипредметные связи, творчески применять полученные знания в незнакомой ситуации.
Письменная работа или устная презентация не должны содержать ошибок или недочетов.
Оценка "4":
Знания всего изученного программного материала.
Умения выделять главные положения в изученном материале, на основании фактов и примеров обобщать, делать выводы, устанавливать внутрипредметные связи, применять полученные знания на практике.
Допускаются незначительные (негрубые) ошибки и недочёты при выполнении работы в предложенной форме.
Оценка "3" (уровень представлений, сочетающихся с элементами научных понятий):
Знания и усвоения материала на уровне минимальных требований программы, затруднения при самостоятельном воспроизведении, необходимости незначительной помощи преподавателя.
Умения работать на уровне воспроизведения, затруднения при ответах на видоизменённые вопросы.
Наличия грубой ошибки, нескольких негрубых ошибок при воспроизведении изученного материала, незначительного несоблюдения основных правил культуры письменной и устной речи, правил оформления письменных работ.
Оценка "2":
Знания и усвоения материала на уровне ниже минимальных требований программы, отдельных представлений об изученном материале.
Отсутствия умений работать на уровне репродукции, затруднения при ответах на стандартные вопросы.
Наличия нескольких грубых ошибок, большого числа негрубых ошибок при предъявлении изученного материала, несоблюдения основных правил культуры письменной и устной речи, правил оформления письменных работ.
2. Устный ответ
Оценка "5" ставится, если обучающийся:
показывает глубокое и полное знание и понимание всего объёма программного материала; полное понимание сущности рассматриваемых понятий, явлений и закономерностей, теорий, взаимосвязей;
умеет составлять полный и правильный ответ на основе изученного материала; выделять главные положения, самостоятельно подтверждать ответ конкретными примерами, фактами; самостоятельно и аргументированно делать анализ, обобщения, выводы. Устанавливать межпредметные (на основе ранее приобретенных знаний) и внутрипредметные связи, творчески применять полученные знания в незнакомой ситуации. Последовательно, чётко, связно, обоснованно и безошибочно излагать учебный материал; давать ответ в логической последовательности с использованием принятой терминологии; делать собственные выводы; формулировать точное определение и истолкование основных понятий, законов, теорий; при ответе не повторять дословно текст учебника; излагать материал литературным языком; правильно и обстоятельно отвечать на дополнительные вопросы учителя. Самостоятельно и рационально использовать наглядные пособия, справочные материалы, учебник, дополнительную литературу, первоисточники; применять систему условных обозначений при ведении записей, сопровождающих ответ; использование для доказательства выводов из наблюдений и опытов;
самостоятельно, уверенно и безошибочно применяет полученные знания в решении проблем на творческом уровне; допускает не более одного недочёта, который легко исправляет по требованию учителя; имеет необходимые навыки работы с приборами, чертежами, схемами и графиками, сопутствующими ответу; записи, сопровождающие ответ, соответствуют требованиям.
Оценка "4" ставится, если обучающийся:
показывает знания всего изученного программного материала. Даёт полный и правильный ответ на основе изученных теорий; допускает незначительные ошибки и недочёты при воспроизведении изученного материала, небольшие неточности при использовании научных терминов или в выводах и обобщениях из наблюдений и опытов; материал излагает в определенной логической последовательности, при этом допускает одну негрубую ошибку или не более двух недочетов и может их исправить самостоятельно при требовании или при небольшой помощи преподавателя; в основном усвоил учебный материал; подтверждает ответ конкретными примерами; правильно отвечает на дополнительные вопросы учителя.
умеет самостоятельно выделять главные положения в изученном материале; на основании фактов и примеров умеет обобщать, делать выводы, устанавливать внутрипредметные связи; умеет применять полученные знания на практике в видоизменённой ситуации, соблюдать основные правила культуры устной речи и сопровождающей письменной, использовать научные термины;
не обладает достаточным навыком работы со справочной литературой, учебником, первоисточниками (правильно ориентируется, но работает медленно); допускает негрубые нарушения правил оформления письменных работ.
Оценка "3" ставится, если обучающийся:
имеет пробелы в усвоении материала, не препятствующие дальнейшему усвоению программного материала;
материал излагает несистематизированно, фрагментарно, не всегда последовательно;
показывает недостаточную сформированность отдельных знаний и умений; выводы и обобщения аргументирует слабо, допускает в них ошибки.
допускает ошибки и неточности в использовании научной терминологии, определения понятий дает недостаточно четкие;
не использует в качестве доказательства выводы и обобщения из наблюдений, фактов, опытов или допускает ошибки при их изложении;
испытывает затруднения в применении знаний, необходимых для решения задач различных типов, при объяснении конкретных явлений на основе теорий и законов, или в подтверждении конкретных примеров практического применения теорий;
отвечает неполно на вопросы учителя (упуская и основное) или воспроизводит содержание текста учебника, но недостаточно понимает отдельные положения, имеющие важное значение в этом тексте;
обнаруживает недостаточное понимание отдельных положений при воспроизведении текста учебника (записей, первоисточников) или отвечает неполно на вопросы учителя, допуская одну-две грубые ошибки.
Оценка "2" ставится, если обучающийся:
не усваивает и не раскрывает основное содержание материала;
не делает выводов и обобщений.
не знает и не понимает значительную или основную часть программного материала в пределах поставленных вопросов;
имеет слабо сформированные и неполные знания и не умеет применять их к решению конкретных вопросов и задач по образцу;
при ответе (на один вопрос) допускает более двух грубых ошибок, которые не может исправить даже при помощи учителя.
Оценка "1" ставится, если обучающийся:
Примечание
По окончании устного ответа, после презентации или защиты обучающимся проекта педагогом даётся краткий комментарий к ответу или иному предъявлению знаний и компетенций, объявляется мотивированная оценка.
3. Оценка самостоятельных письменных и контрольных работ
Оценка "5" ставится, если обучающийся:
Оценка "4" ставится, если обучающийся выполнил работу полностью, но допустил в ней:
Оценка "3" ставится, если обучающийся правильно выполнил не менее половины работы или допустил:
не более двух грубых ошибок;
не более одной грубой и одной негрубой ошибки и одного недочета;
не более двух-трех негрубых ошибок;
не более одной негрубой ошибки и трех недочетов;
при отсутствии ошибок, но при наличии четырех-пяти недочетов.
Оценка "2" ставится, если обучающийся:
допустил число ошибок и недочетов, превосходящее норму, при которой может быть выставлена оценка "3";
правильно выполнил менее половины работы.
Оценка "1" ставится, если обучающийся:
Примечание. Учитель имеет право поставить обучающемуся оценку выше той, которая предусмотрена нормами, если обучающимся оригинально выполнена работа, найден нетипичный вариант решения, выдвинуты и обоснованы гипотезы.
4. Оценка выполнения практических (лабораторных) работ, опытов по предметам.
Оценка "5" ставится, если обучающийся:
правильно определил цель опыта;
выполнил работу в полном объеме с соблюдением необходимой последовательности проведения опытов и измерений;
самостоятельно и рационально выбрал и подготовил для опыта необходимое оборудование, все опыты провел в условиях и режимах, обеспечивающих получение результатов и выводов с наибольшей точностью;
научно грамотно, логично описал наблюдения и сформулировал выводы из опыта. В представленном отчете правильно и аккуратно выполнил все записи, таблицы, рисунки, чертежи, графики, вычисления и сделал выводы;
правильно выполнил анализ погрешностей (9-11 классы);
проявил организационно-трудовые умения (поддерживал чистоту рабочего места и порядок на столе, экономно использовал расходные материалы);
эксперимент осуществлял по плану с учетом техники безопасности и правил работы с материалами и оборудованием.
Оценка "4" ставится, если обучающийся выполнил требования к оценке "5", но:
опыт проводил в условиях, не обеспечивающих достаточной точности измерений;
допустил два-три недочета;
допустил не более одной негрубой ошибки и одного недочета,
эксперимент провел не полностью;
в описании наблюдений из опыта допустил неточности, выводы сделал неполные.
Оценка "3" ставится, если обучающийся:
правильно определил цель опыта; работу выполнил правильно не менее чем наполовину, однако объём выполненной части таков, что позволяет получить правильные результаты и выводы по основным, принципиально важным задачам работы;
подбор оборудования, объектов, материалов, а также работы по началу опыта провел с помощью учителя; или в ходе проведения опыта и измерений допустил ошибки в описании наблюдений, формулировании выводов;
опыт проводил в нерациональных условиях, что привело к получению результатов с большей погрешностью; или в отчёте допустил в общей сложности не более двух ошибок (в записях единиц, измерениях, в вычислениях, графиках, таблицах, схемах, анализе погрешностей и т.д.) не принципиального для данной работы характера, но повлиявших на результат выполнения; или не выполнил совсем или выполнил неверно анализ погрешностей (9-11 класс);
допустил грубую ошибку в ходе эксперимента (в объяснении, в оформлении работы, в соблюдении правил техники безопасности при работе с материалами и оборудованием), которая исправляется по требованию учителя.
Оценка "2" ставится, если обучающийся:
не определил самостоятельно цель опыта; выполнил работу не полностью, не подготовил нужное оборудование, и объем выполненной части работы не позволяет сделать правильных выводов;
опыты, измерения, вычисления, наблюдения производил неправильно;
в ходе работы и в отчете обнаружились в совокупности все недостатки, отмеченные в требованиях к оценке "3";
допустил две (и более) грубые ошибки в ходе эксперимента, в объяснении, в оформлении работы, в соблюдении правил техники безопасности при работе с веществами и оборудованием, которые не смог исправить даже по требованию учителя.
Примечание. 1. В тех случаях, когда обучающийся показал оригинальный и наиболее рациональный подход к выполнению работы и в процессе работы, но не избежал тех или иных недостатков, оценка за выполнение работы по усмотрению учителя может быть повышена по сравнению с указанными выше нормами.
2. Оценки с анализом доводятся до сведения обучающихся, как правило, на последующем уроке.
5. Оценка умений проводить наблюдения
Оценка "5" ставится, если обучающийся:
правильно по заданию учителя провел наблюдение;
выделил существенные признаки у наблюдаемого объекта (процесса);
логично, научно, грамотно оформил результаты наблюдений и выводы.
Оценка "4" ставится, если обучающийся правильно по заданию учителя провел наблюдение.
6. Учебный проект
Критерии оценивания учебного проекта
| Критерии оценивания | 2 (плохо) | 3 (удовлетвори- тельно) | 4 (хорошо) | 5 (отлично) |
| Связь с программой и учебным планом | Проект не связан с действующей школьной программой и учебным планом | Проект в некоторой степени связан с программой и учебным планом; его внедрение возможно только за счет внеклассной работы | Проект связан с программой и учебным планом по предмету, но для его проведения придется использовать резерв времени | Проект полностью ориентирован на действующую программу и учебный план и может быть легко интегрирован в рамках учебного процесса
|
| Содержание проекта | Нет логической последовательнос-ти, в изложении материала были допущены ошибки. Отсутствуют са-мостоятельные исследования обучающихся. Нет деятельности обучающихся, связанной с уме-ниями находить, описывать и сум-мировать инфор-мацию | Материал проекта дается более или менее логично, но не понятны отдельные вопросы. Самостоя-тельные исследова-ния обучающихся не затрагивают основополагающие вопросы | Материал изложен логично, между его частями сделаны плавные переходы. Самостоятельные исследования учащихся частично иллюстрируют основополагающие вопросы | Содержание проекта понятно, представлено логично и удобно для восприятия. Самостоятельные исследования учащихся самым понятным образом иллюстрируют основополагающие вопросы |
| Работа в группах | Роли между участ-никами проекта распределены не были, коллективная деятельность практически не осуществлялась, некоторые члены группы вообще не работали над проектом | Большинство членов группы участвовали в работе над проектом, однако нагрузка между ними была рас-пределена неравномерно | Большинство членов группы внесли свой вклад в работу группы | Работу над проектом в равной мере осуществляли все члены группы Графический |
| Представление результатов работы | Тема раскрыта частично. Наблюю-дается расплывча-тая формулировка проблемы, целей, выводов | Выбор формы представления результатов не обоснован. Объем информации, ил-люстративный материал недоста-точен | В основном материал изложен последовательно, логически связно, но не всегда достаточно аргу-ментированно и полно | Выбор формы представления результатов Иллюстративный материал соот-ветствует содер-жанию, дополняет представленную информацию |
| Организация применения проекта в школе | Описание учебного проекта непонятно, не ясно, каким об-разом он будет внедряться в учебный процесс. Компоненты учебного проекта не завер-шены. Учебный проект невозможно реализовать в урочной дея-тельности
| Описанию учебного проекта не хватает ясности, он не отображает после-довательность ме-роприятий по его внедрению. Компо-ненты учебного проекта либо не завершены, либо недостаточно детализированы. Учебный проект можно реализо-вывать только в собственном классе учителя | Описание учебного проекта отображает последователь-ность мероприятий по его внедрению, но некоторые аспекты непонят-ны. Компоненты учебного проекта являются завер-шенными, но не-достаточно дета-лизированными, чтобы их эффек-тивно использо-вать. Учебный проект можно реализовывать в разноуровневом обучении | Описание учебного проекта отображает четкую последо-вательность мероприятий по его внедрению. Ком-поненты учебного проекта хорошо подготовлены для использования. Учебный проект легко модифици-ровать и реализо-вывать в разноу-ровневом обуче-нии |
1. Оценка письменных контрольных работ обучающихся по математике.
Ответ оценивается отметкой «5», если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Отметка «1» ставится, если:
Общая классификация ошибок.
При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.
3.1. Грубыми считаются ошибки:
незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
незнание наименований единиц измерения;
неумение выделить в ответе главное;
неумение применять знания, алгоритмы для решения задач;
неумение делать выводы и обобщения;
неумение читать и строить графики;
неумение пользоваться первоисточниками, учебником и справочниками;
потеря корня или сохранение постороннего корня;
отбрасывание без объяснений одного из них;
равнозначные им ошибки;
вычислительные ошибки, если они не являются опиской;
логические ошибки.
3.2. К негрубым ошибкам следует отнести:
неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;
неточность графика;
нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
нерациональные методы работы со справочной и другой литературой;
неумение решать задачи, выполнять задания в общем виде.
3.3. Недочетами являются:
нерациональные приемы вычислений и преобразований;
небрежное выполнение записей, чертежей, схем, графиков.
ПРИЛОЖЕНИЕ 2.
Формы контроля знаний, умений, навыков (стартового, промежуточного, рубежного, итогового.)
Предметом педагогического контроля по алгебре является оценка результатов организованного в нем педагогического процесса. Основным предметом оценки результатов музыкального образования являются знания, результатов обучения – умения, навыки и результатов воспитания – мировоззренческие установки, интересы, мотивы и потребности личности.
Стартовый контроль в начале года. Он определяет исходный уровень обученности. Контрольная работа или тест.
Текущий контроль в форме самостоятельных работы. С помощью текущего контроля возможно диагностирование дидактического процесса, выявление его динамики, сопоставление результатов обучения на отдельных его этапах.
Рубежный контроль выполняет этапное подведение итогов за полугодие после прохождения тем в форме теста.
Заключительный контроль. Методы диагностики - проект, викторина, тест.
Внеурочная деятельность по предмету предусматривается в формах: участие в конкурсах, заочных олимпиадах, творческие проекты.
5






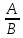 0 и
0 и 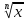 (х ≥ 0). Степень с рациональным показателем и ее свойства.
(х ≥ 0). Степень с рациональным показателем и ее свойства.



















