РАЗДЕЛ 1. Планируемые результаты освоения учебного предмета.
Личностными УУД результатами изучения предмета «Математика» являются следующие качества:
– независимость и критичность мышления;
– воля и настойчивость в достижении цели.
Средством достижения этих результатов является:
– система заданий учебников;
– представленная в учебниках в явном виде организация материала по принципу минимакса;
– использование совокупности технологий, ориентированных на развитие самостоятельности и критичности мышления: технология системно- деятельностного подхода в обучении, технология оценивания.
Метапредметными результатами изучения курса «Математика» является формирование универсальных учебных действий (УУД).
Регулятивные УУД:
– самостоятельно обнаруживать и формулировать проблему в классной и индивидуальной учебной деятельности;
– выдвигать версии решения проблемы, осознавать конечный результат, выбирать средства достижения цели из предложенных или их искать самостоятельно;
– составлять (индивидуально или в группе) план решения проблемы (выполнения проекта);
– подбирать к каждой проблеме (задаче) адекватную ей теоретическую модель;
– работая по предложенному или самостоятельно составленному плану, использовать наряду с основными и дополнительные средства (справочная литература, сложные приборы, компьютер);
– планировать свою индивидуальную образовательную траекторию;
– работать по самостоятельно составленному плану, сверяясь с ним и с целью деятельности, исправляя ошибки, используя самостоятельно подобранные средства (в том числе и Интернет);
– свободно пользоваться выработанными критериями оценки и самооценки, исходя из цели и имеющихся критериев, различая результат и способы действий;
– в ходе представления проекта давать оценку его результатам;
– самостоятельно осознавать причины своего успеха или неуспеха и находить способы выхода из ситуации неуспеха;
– уметь оценить степень успешности своей индивидуальной образовательной деятельности;
– давать оценку своим личностным качествам и чертам характера («каков я»), определять направления своего развития («каким я хочу стать», «что мне для этого надо сделать»).
Средством формирования регулятивных УУД служат технология системно - деятельностного подхода на этапе изучения нового материала и технология оценивания образовательных достижений (учебных успехов).
Познавательные УУД:
– анализировать, сравнивать, классифицировать и обобщать факты и явления;
– осуществлять сравнение, сериацию и классификацию, самостоятельно выбирая основания и критерии для указанных логических операций; строить классификацию путём дихотомического деления (на основе отрицания);
– строить логически обоснованное рассуждение, включающее установление причинно-следственных связей;
– создавать математические модели;
– составлять тезисы, различные виды планов (простых, сложных и т.п.). Преобразовывать информацию из одного вида в другой (таблицу в текст, диаграмму и пр.);
– вычитывать все уровни текстовой информации.
– уметь определять возможные источники необходимых сведений, производить поиск информации, анализировать и оценивать её достоверность.
– понимая позицию другого человека, различать в его речи: мнение (точку зрения), доказательство (аргументы), факты; гипотезы, аксиомы, теории. Для этого самостоятельно использовать различные виды чтения (изучающее, просмотровое, ознакомительное, поисковое), приёмы слушания.
– самому создавать источники информации разного типа и для разных аудиторий, соблюдать информационную гигиену и правила информационной безопасности;
– уметь использовать компьютерные и коммуникационные технологии как инструмент для достижения своих целей. Уметь выбирать адекватные задаче инструментальные программно-аппаратные средства и сервисы.
Средством формирования познавательных УУД служат учебный материал и прежде всего продуктивные задания учебника.
– Использование математических знаний для решения различных математических задач и оценки полученных результатов.
– Совокупность умений по использованию доказательной математической речи.
– Совокупность умений по работе с информацией, в том числе и с различными математическими текстами.
– Умения использовать математические средства для изучения и описания реальных процессов и явлений.
– Независимость и критичность мышления.
– Воля и настойчивость в достижении цели.
Коммуникативные УУД:
– самостоятельно организовывать учебное взаимодействие в группе (определять общие цели, договариваться друг с другом и т.д.);
– отстаивая свою точку зрения, приводить аргументы, подтверждая их фактами;
– в дискуссии уметь выдвинуть контраргументы;
– учиться критично относиться к своему мнению, с достоинством признавать ошибочность своего мнения (если оно таково) и корректировать его;
– понимая позицию другого, различать в его речи: мнение (точку зрения), доказательство (аргументы), факты; гипотезы, аксиомы, теории;
– уметь взглянуть на ситуацию с иной позиции и договариваться с людьми иных позиций.
Средством формирования коммуникативных УУД служат технология проблемного обучения, организация работы в малых группах, также использование на уроках технологии личностно-ориентированного и системно - деятельностного обучения.
Предметными результатами изучения предмета «Математика» являются следующие умения.
В ходе освоения содержания математического образования учащиеся овладевают разнообразными способами деятельности, приобретают и совершенствуют опыт:
построения и исследования математических моделей для описания и решения прикладных задач, задач из смежных дисциплин;
выполнения и самостоятельного составления алгоритмических предписаний и инструкций на математическом материале; выполнения расчетов практического характера; использования математических формул и самостоятельного составления формул на основе обобщения частных случаев и эксперимента;
самостоятельной работы с источниками информации, обобщения и систематизации полученной информации, интегрирования ее в личный опыт;
проведения доказательных рассуждений, логического обоснования выводов, различения доказанных и недоказанных утверждений, аргументированных и эмоционально убедительных суждений;
самостоятельной и коллективной деятельности, включения своих результатов в результаты работы группы, соотнесение своего мнения с мнением других участников учебного коллектива и мнением авторитетных источников.
В результате изучения математики ученик должен: знать/понимать
существо понятия математического доказательства; примеры доказательств;
существо понятия алгоритма; примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации
РАЗДЕЛ 2. Содержание учебного предмета
1. Простейшие функции и графики (25 ч). Числовые неравенства. Множества чисел. Функция, график функции. Функции y = x, y = x2, 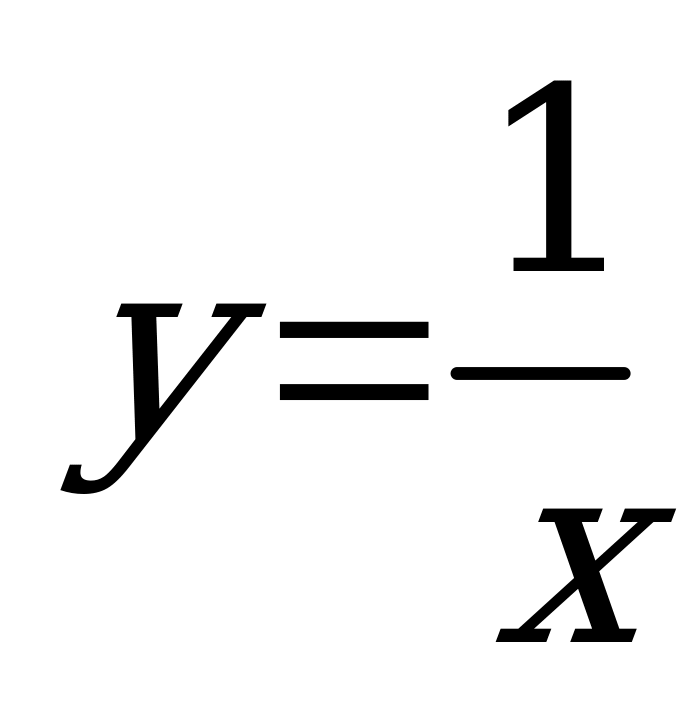 , их свойства и графики.
, их свойства и графики.
Основная цель — ввести понятие функции и ее графика, изучить свойства простейших функций, и их графики.
При изучении данной темы рассматриваются свойства числовых неравенств, изображение числовых промежутков на координатной оси, вводятся понятия функции и ее графика, показываются примеры простейших функций (y = x, y = x2, 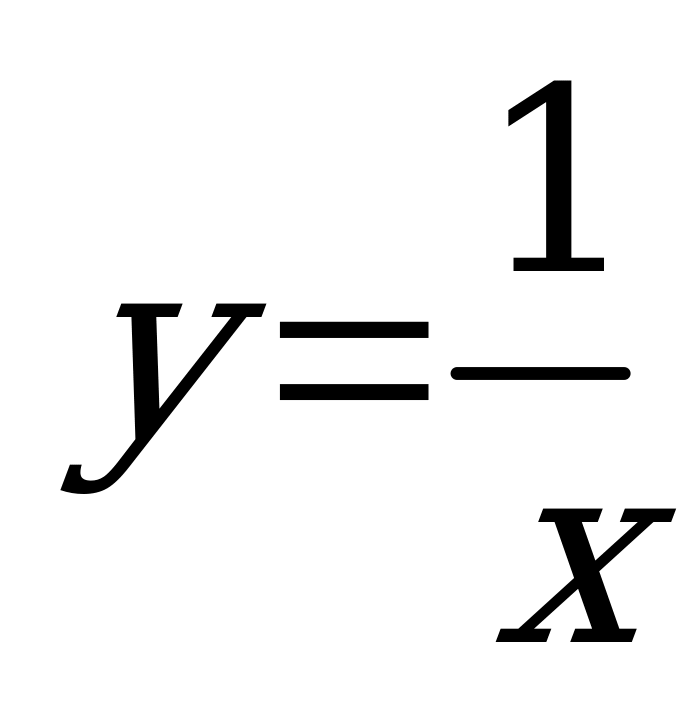 ), изучаются их свойства и графики. При доказательстве свойств функций используются свойства неравенств. На интуитивной основе вводятся понятия непрерывности функции и непрерывности графика функции, играющие важную роль при доказательстве существования квадратного корня из положительного числа.
), изучаются их свойства и графики. При доказательстве свойств функций используются свойства неравенств. На интуитивной основе вводятся понятия непрерывности функции и непрерывности графика функции, играющие важную роль при доказательстве существования квадратного корня из положительного числа.
Из дополнения к главе I рекомендуется рассмотреть сведения о пересечении и объединении множеств, показать соответствующую символику.
Квадратные корни
Квадратный корень, арифметический квадратный корень, приближенное вычисление квадратных корней, свойства арифметических квадратных корней, преобразование выражений, содержащих квадратные корни.
Основная цель — освоить понятие квадратного корня и арифметического квадратного корня, выработать умение преобразовывать выражения, содержащие квадратные корни.
Существование квадратного корня из положительного числа показывается с опорой на непрерывность графика функции y = x2, доказывается иррациональность квадратного корня из любого числа, не являющегося квадратом натурального числа. Основное внимание следует уделить изучению свойств квадратных корней и их использованию для преобразования выражений, содержащих квадратные корни. Учащиеся должны освоить вынесение множителя из-под знака корня, внесение множителя под знак корня и освобождение дроби от иррациональности в знаменателе в простых случаях.
2.Квадратные и рациональные уравнения (29ч). Квадратные уравнения
Квадратный трехчлен. Квадратное уравнение. Теорема Виета. Применение квадратных уравнений к решению задач.
Основная цель — выработать умения решать квадратные уравнения, и решать задачи, сводящиеся к ним.
Изучение данной темы начинается с рассмотрения квадратного трехчлена, выяснения условий, при которых его можно разложить на два одинаковых или на два разных множителя. На этой основе вводится понятие квадратного уравнения и его корня, рассматриваются способы решения неполного квадратного уравнения и квадратного уравнения общего вида, приведенного квадратного уравнения. Доказываются теоремы Виета (прямая и обратная), показывается применение квадратных уравнений для решения задач.
Применение квадратного уравнения существенно расширяет круг текстовых задач, которые можно предложить учащимся, дает хорошую возможность для обсуждения некоторых общих идей, связанных с их решением.
Рациональные уравнения.
Рациональное уравнение. Биквадратное уравнение. Распадающееся уравнение. Уравнение, одна часть которого алгебраическая дробь, а другая равна нулю. Решение задач при помощи рациональных уравнений.
Основная цель — выработать умения решать рациональные уравнения и использовать их для решения текстовых задач.
При изучении данной темы вводится понятие рационального уравнения, рассматриваются наиболее часто используемые виды рациональных уравнений: биквадратное, распадающееся (одна часть уравнения произведение нескольких множителей, зависящих от x, а другая равна нулю), уравнение, одна часть которого алгебраическая дробь, а другая равна нулю; показываются применение рациональных уравнений для решения текстовых задач.
Следует обратить внимание на то, что при решении рациональных уравнений, содержащих алгебраическая дробь, уравнение не умножается на выражение с неизвестным, а преобразуется к уравнению, одна часть которого алгебраическая дробь, а другая равна нулю. Идея решения рациональных уравнений заменой неизвестных показывается на примере биквадратных уравнений, а в классах с углубленным изучением математики соответствующее умение отрабатывается на достаточно сложных примерах.
3. Линейная и квадратичная функции (23 ч).
Прямая пропорциональная зависимость, график функции y = kx. Линейная функция и ее график. Равномерное движение.
Основная цель — ввести понятие прямой пропорциональной зависимости (функции y = kx) и линейной функции, выработать умения решать задачи, связанные с графиками этих функций.
При изучении данной темы расширяется круг изучаемых функций, появляется новая идея построения графиков — с помощью переноса. Сначала изучается частный случай линейной функции — прямая пропорциональная зависимость, исследуется расположение прямой в зависимости от углового коэффициента, решаются традиционные задачи, связанные с принадлежностью графику заданных точек, знаком функции и т. п. Затем вводится понятие линейной функции, показывается, как можно получить график линейной функции из соответствующего графика прямой пропорциональности. При этом показывается перенос графика по осям Ox и Oy. Это необходимо не только для уяснения учащимися взаимосвязи между частным и общим случаями линейной функции, но и с пропедевтической целью — для подготовки учащихся к переносу других графиков. Однако основным способом построения графика линейной функции остается построение прямой по двум точкам.
Рассмотрение графиков прямолинейного движения позволяет рассмотреть примеры кусочно заданных функций, способствует упрочению межпредметных связей между математикой и физикой.
Рекомендуется рассмотреть функцию y = │x│, переносы ее графика по осям координат для подготовки учащихся к изучению следующей темы.
Квадратичная функця .
Квадратичная функция и ее график.
Основная цель — изучить квадратичную функцию и ее график, выработать умения решать задачи, связанные с графиком квадратичной функции.
Изучение данной темы начинается с функции y = ax2 (сначала для a 0, потом для a ≠ 0) и изучения ее свойств, тут же иллюстрируемых на графиках. График функции y = a(x – xo)2 + yo получается переносом графика функции y = ax2. Это необходимо для уяснения учащимися взаимосвязи между частным и общим случаями квадратичной функции. Большое внимание уделяется построению графика квадратичной функции по точкам с вычислением абсциссы вершины параболы. Рассмотрение графика движения тела в поле притяжения Земли дает еще один пример межпредметных связей между математикой и физикой, позволяет показать применение изучаемого материала на примере задач с физическим содержанием.
4.Системы рациональных уравнений (19 ч). Системы рациональных уравнений. Системы уравнений первой и второй степени. Решение задач при помощи систем уравнений первой и второй степени, систем рациональных уравнений.
Основная цель — выработать умения решать системы уравнений первой и второй степени, системы рациональных уравнений, задачи, приводящие к таким системам.
Изучение данной темы начинается с введения понятия системы рациональных уравнений, ее решения. Многие определения и приемы действий учащимся знакомы из 7 класса, когда они решали системы линейных уравнений. Поэтому новый материал надо излагать после повторения ранее изученного.
Графический способ решения систем уравнений
Графический способ решения систем двух уравнений с двумя неизвестными и исследования системы двух уравнений первой степени с двумя неизвестными. Решение систем уравнений и уравнений графическим способом. Решение уравнений в целых числах.
5. Повторение (6 ч).
РАЗДЕЛ 3. .Тематическое планирование, в том числе с учетом рабочей программы воспитания
Реализация рабочей программы воспитания в урочной деятельности направлена на формирование понимания важнейших социокультурных и духовно-нравственных ценностей
Механизм реализации рабочей программы воспитания:
- привлечение внимания обучающихся к ценностному аспекту изучаемых на уроках явлений, организация их работы с получаемой на уроке социально значимой информацией
– инициирование ее обсуждения, высказывания обучающимися своего мнения по ее поводу, выработки своего к ней отношения;
- применение на уроке интерактивных форм работы с обучающимися: интеллектуальных игр, стимулирующих познавательную мотивацию обучающихся; проведение предметных олимпиад, турниров, викторин, квестов, игр-экспериментов, дискуссии и др.
- демонстрация примеров гражданского поведения, проявления добросердечности через подбор текстов для чтения, задач для решения, проблемных ситуаций для обсуждения, анализ поступков людей и др.
- применение на уроках групповой работы или работы в парах, которые учат обучающихся командной работе и взаимодействию с другими обучающимися; включение в урок игровых процедур, которые помогают поддержать мотивацию обучающихся к получению знаний, налаживанию позитивных межличностных отношений в классе, помогают установлению доброжелательной атмосферы во время урока.
- посещение экскурсий, музейные уроки, библиотечные уроки и др.
- приобщение обучающихся к российским традиционным духовным ценностям, включая культурные ценности своей этнической группы, правилам и нормам поведения в российском обществе.
- побуждение обучающихся соблюдать на уроке общепринятые нормы поведения, правила общения, принципы учебной дисциплины, самоорганизации, взаимоконтроль и самоконтроль
- организация шефства мотивированных и эрудированных обучающихся над их неуспевающими одноклассниками, дающего обучающимся социально значимый опыт сотрудничества и взаимной помощи.
- инициирование и поддержка исследовательской деятельности обучающихся в рамках реализации ими индивидуальных и групповых исследовательских проектов, что даст обучающимся возможность приобрести навык самостоятельного решения теоретической проблемы, навык генерирования и оформления собственных идей, навык уважительного отношения к чужим идеям, оформленным в работах других исследователей, навык публичного выступления перед аудиторией, аргументирования и отстаивания своей точки зрения.
- знакомство обучающихся с профессиями через подбор задач для решения, связанных с профессиональной деятельностью, проблемных ситуаций для обсуждения, организацию профессиональных проб обучающихся
Тематическое планирование
| № урока | Тема урока | Кол-во часов |
| 1-2 | Числовые неравенства | 2 |
| 3 | Координатная ось | 1 |
| 4-5 | Множества чисел | 2 |
| 6 | Декартова система координат на плоскости | 1 |
| 7-8 | Понятие функции РПВ Устный журнал «Новый взгляд на привычные вещи» | 2 |
| 9 | Понятие графика функции РПВ Диспут Графическое изображение зависимости» | 1 |
| 10-11 | Функция y=x и её график | 2 |
| 12 | Функция y=x2 | 1 |
| 13 | График функции y=x2 | 1 |
| 14 | Функция y= 1\ х | 1 |
| 15 | График функции y= 1\ х | 1 |
| 16 | Контрольная работа №1 по теме «Функции и графики» | 1 |
| 17-18 | Понятие квадратного корня | 2 |
| 19-20 | Арифметический квадратный корень | 2 |
| 21-23 | Свойства арифметических квадратных корней | 3 |
| 24 | Квадратный корень из натурального числа РПВ Аукцион знаний «Применение арифметического квадратного корня» | 1 |
| 25 | Контрольная работа №2 по теме «Квадратные корни» | 1 |
| 26-27 | Квадратный трехчлен | 2 |
| 28-29 | Понятие квадратного уравнения РПВ Дискуссия «Математические споры» | 2 |
| 30-31 | Неполное квадратное уравнение | 2 |
| 32-34 | Решение квадратного уравнения общего вида | 3 |
| 35-36 | Приведенное квадратное уравнение | 2 |
| 37-38 | Теорема Виета | 2 |
| 39-40 | Применение квадратных уравнений к решению задач РПВ Аукцион знаний «Новый подход к классическим задачам» | 2 |
| 41 | Контрольная работа №3 «Квадратные уравнения» | 1 |
| 42 | Понятие рационального уравнения | 1 |
| 43-44 | Биквадратное уравнение | 2 |
| 45-46 | Распадающееся уравнение РПВ Слабое звено «Квадратные уравнения» | 2 |
| 47-49 | Уравнение, одна часть которого алгебраическая дробь, а другая - нуль | 3 |
| 50-51 | Решение рациональных уравнений | 2 |
| 52-53 | Решение задач при помощи рациональных уравнений | 2 |
| 54 | Контрольная работа №4 по теме «Рациональные уравнения» | 1 |
| 55-56 | Прямая пропорциональность | 2 |
| 57-58 | График функции y=kx | 2 |
| 59-61 | Линейная функция и её график | 3 |
| 62 | Равномерное движение РПВ Лекция «Математика и физика. Точки соприкосновения» | 1 |
| 63 | Функция y=|x| и её график | 1 |
| 64-65 | Функция y=ax2 (а0) | 2 |
| 66-67 | Функция y=ax2 (а≠0) | 2 |
| 68-70 | График функции y=a(x-x0)2+ y0 | 3 |
| 71-72 | Квадратичная функция и её график РПВ Кейс «Решение задач графическим методом» | 2 |
| 73 | Обратная пропорциональность | 1 |
| 74 | Функция y=k/x (k0) | 1 |
| 75 | Функция y=k/x (k≠0) | 1 |
| 76 | Дробно-линейная функция и её график | 1 |
| 77 | Контрольная работа №5 по теме «Линейная и квадратичная функции» | 1 |
| 78-79 | Понятие системы рациональных уравнений | 2 |
| 80-82 | Решение систем рациональных уравнений способом подстановки | 3 |
| 83 | Решение систем рациональных уравнений другими способами | 1 |
| 84-87 | Решение задач при помощи систем рациональных уравнений РПВ Музейный урок | 4 |
| 88-89 | Графический способ решения систем двух уравнений первой степени с двумя неизвестными | 2 |
| 90-91 | Графический способ исследования системы двух уравнений первой степени с двумя неизвестными | 2 |
| 92-93 | Решение систем уравнений первой и второй степени графическим способом | 2 |
| 94-95 | Примеры решения уравнений графическим способом | 2 |
| 96 | Контрольная работа №6 по теме «Системы рациональных уравнений» | 1 |
| 97 | Функции и графики | 1 |
| 98 | Функции y=kx+b, y=ax2+bx+c, y=k/(x-x0)+y0 | 1 |
| 99 | Квадратные корни РПВ Аукцион математических знаний | 1 |
| 100 | Квадратные и рациональные уравнения | 1 |
| 101 | Системы рациональных уравнений | 1 |
| 102 | Итоговая контрольная работа | 1 |
ПРИЛОЖЕНИЕ
Календарно-тематическое планирование.
| № урока | № пункта | Тема урока | Кол-во часов | Домашнее задание | Дата |
| По плану | Фактически |
| Глава I. Простейшие функции. Квадратные корни (25 ч.) |
| §1. Функции и графики | 9 |
|
|
|
| 1 | 1.1 | Числовые неравенства | 1 | п. 1.1 в. 1,2 стр. 9 № 10 |
|
|
| 2 | 1.1 | Числовые неравенства | 1 | п. 1.1 № 13, 17 |
|
|
| 3 | 1.2 | Координатная ось | 1 | п. 1.2 № 23 (2 ст.), № 26 (е-к) |
|
|
| 4 | 1.3 | Множества чисел | 1 | п. 1.3 в. 30 стр. 17 № 37, № 40 |
|
|
| 5 | 1.3 | Множества чисел | 1 | п. 1.3 № 41, № 42 (2 ст.) |
|
|
| 6 | 1.4 | Декартова система координат на плоскости | 1 | п. 1.4 в. 43, 44 стр. 21 № 47, № 50. Приготовить сообщение № 52 |
|
|
| 7 | 1.5 | Понятие функции | 1 | п. 1.5 в. 53 стр. 25 № 55, 58 |
|
|
| 8 | 1.5 | Понятие функции | 1 | п. 1.5 № 62, № 64 (б). Приготовить сообщение № 65 |
|
|
| 9 | 1.6 | Понятие графика функции | 1 | п. 1.6 в. 66, 67 стр. 28 № 70, № 72 |
|
|
| §2. Функции y=x, y=x2, y= 1\ х | 7 |
|
|
|
| 10 | 2.1 | Функция y=x и её график | 1 | п. 2.1 в. 73 стр. 32 № 76, № 78 |
|
|
| 11 | 2.1 | Функция y=x и её график | 1 | п. 2.1 № 82, № 84 |
|
|
| 12 | 2.2 | Функция y=x2 | 1 | п. 2.2 в. 86 стр. 34 № 88, № 94 |
|
|
| 13 | 2.3 | График функции y=x2 | 1 | п. 2.3 в. 98 стр. 38 № 101, № 103 |
|
|
| 14 | 2.4 | Функция y= 1\ х | 1 | п. 2.4 в. 104 стр. 40 № 107, № 110 |
|
|
| 15 | 2.5 | График функции y= 1\ х | 1 | п. 2.5 в. 111 стр. 44 № 116, № 120 |
|
|
| 16 |
| Контрольная работа №1 по теме «Функции и графики» | 1 | Повторить |
|
|
| §3. Квадратные корни | 9 |
|
|
|
| 17 | 3.1 | Понятие квадратного корня | 1 | п. 3.1 в. 121, 122 стр. 47 № 125, № 127 (в, г, ж, з) |
|
|
| 18 | 3.1 | Понятие квадратного корня | 1 | п. 3.1 № 129 (г-з) |
|
|
| 19 | 3.2 | Арифметический квадратный корень | 1 | п. 3.2 в. 130 стр. 49 № 133, № 138 (б, в) |
|
|
| 20 | 3.2 | Арифметический квадратный корень | 1 | п. 3.2 № 140 (в, ж-и), № 143 (г-е) |
|
|
| 21 | 3.3 | Свойства арифметических квадратных корней | 1 | п. 3.3 в. 144 стр. 53 № 153, № 156 |
|
|
| 22 | 3.3 | Свойства арифметических квадратных корней | 1 | п. 3.3 № 157 (2 ст.), № 167 (ж-о) |
|
|
| 23 | 3.3 | Свойства арифметических квадратных корней | 1 | п. 3.3 № 170, № 172 (2 ст.) |
|
|
| 24 | 3.4 | Квадратный корень из натурального числа | 1 | п. 3.4 в. 176 стр. 59 № 181, № 182 (2 ст.) |
|
|
| 25 |
| Контрольная работа №2 по теме «Квадратные корни» | 1 | Повторить |
|
|
| Глава II. Квадратные и рациональные уравнения (29 ч.) |
| §4. Квадратные уравнения | 16 |
|
|
|
| 26 | 4.1 | Квадратный трехчлен | 1 | п. 4.1 в. 198 стр. 72 № 201, № 203 (ж-м) |
|
|
| 27 | 4.1 | Квадратный трехчлен | 1 | п. 4.1 № 207, № 209 (в, е, ж) |
|
|
| 28 | 4.2 | Понятие квадратного уравнения | 1 | п. 4.2 в. 211 стр. 75 № 216 |
|
|
| 29 | 4.2 | Понятие квадратного уравнения | 1 | п. 4.2 в. 220 стр. 76 № 219 (б, г), № 221 (г-е) |
|
|
| 30 | 4.3 | Неполное квадратное уравнение | 1 | п. 4.3 в. 222, 223 стр. 78 № 224 (2 ст.), № 228 (2 ст.) |
|
|
| 31 | 4.3 | Неполное квадратное уравнение | 1 | п. 4.3 № 230 (е-и), № 232 (2 ст.); № 236 (б) - дополнительно |
|
|
| 32 | 4.4 | Решение квадратного уравнения общего вида | 1 | п. 4.4 в. 237, 238 стр. 83 № 240 (2 ст.), № 242 (2 ст.) |
|
|
| 33 | 4.4 | Решение квадратного уравнения общего вида | 1 | п. 4.4 № 243 (д-з), № 245 (2 ст.) |
|
|
| 34 | 4.4 | Решение квадратного уравнения общего вида | 1 | п. 4.4 № 247 (2 ст.), № 250; № 254 (2 ст) - дополнительно |
|
|
| 35 | 4.5 | Приведенное квадратное уравнение | 1 | п. 4.5 в. 255, 256 стр. 87 № 257 (2 ст.) |
|
|
| 36 | 4.5 | Приведенное квадратное уравнение | 1 | п. 4.5 № 259 (2 ст.), № 260 |
|
|
| 37 | 4.6 | Теорема Виета | 1 | п. 4.6 в. 261,262 стр. 89 № 266, № 271 |
|
|
| 38 | 4.6 | Теорема Виета | 1 | п. 4.6 № 273, № 274. Приготовить сообщение № 279 |
|
|
| 39 | 4.7 | Применение квадратных уравнений к решению задач | 1 | п. 4.7 № 282 (б), № 285 (б, г) |
|
|
| 40 | 4.7 | Применение квадратных уравнений к решению задач | 1 | п. 4.7 № 286 (б), № 287 (б); № 288 - дополнительно |
|
|
| 41 |
| Контрольная работа №3 «Квадратные уравнения» | 1 | Повторить |
|
|
| §5. Рациональные уравнения | 13 |
|
|
|
| 42 | 5.1 | Понятие рационального уравнения | 1 | п. 5.1 в. 290 стр. 95 № 292 (2 ст.), № 293 (е-з) |
|
|
| 43 | 5.2 | Биквадратное уравнение | 1 | п. 5.2 в. 294 стр. 98 № 297 (2 ст.) |
|
|
| 44 | 5.2 | Биквадратное уравнение | 1 | п. 5.2 № 299 (2 ст.) |
|
|
| 45 | 5.3 | Распадающееся уравнение | 1 | п. 5.3 в. 300 стр. 100 № 304 (2 ст.), № 303 (3 ст.) |
|
|
| 46 | 5.3 | Распадающееся уравнение | 1 | п. 5.3 № 305 (з-о) |
|
|
| 47 | 5.4 | Уравнение, одна часть которого алгебраическая дробь, а другая - нуль | 1 | п. 5.4 в. 307 стр. 103 № 311 (2 ст.) |
|
|
| 48 | 5.4 | Уравнение, одна часть которого алгебраическая дробь, а другая - нуль | 1 | п. 5.4 № 313 |
|
|
| 49 | 5.4 | Уравнение, одна часть которого алгебраическая дробь, а другая - нуль | 1 | п. 5.4 № 314 (2 ст.) |
|
|
| 50 | 5.5 | Решение рациональных уравнений | 1 | п. 5.5 в. 316 стр. 106 № 319, № 321 (б, г) |
|
|
| 51 | 5.5 | Решение рациональных уравнений | 1 | п. 5.5 № 323; № 324 - дополнительно |
|
|
| 52 | 5.6 | Решение задач при помощи рациональных уравнений | 1 | п. 5.6 № 327 (б), № 328 |
|
|
| 53 | 5.6 | Решение задач при помощи рациональных уравнений | 1 | п. 5.6 № 334, № 336 |
|
|
| 54 |
| Контрольная работа №4 по теме «Рациональные уравнения» | 1 | Повторить |
|
|
| Глава III. Функции y=kx+b, y=ax2+bx+c, y=k/(x-x0)+y0 (23 ч.) |
| §6. Линейная функция | 9 |
|
|
|
| 55 | 6.1 | Прямая пропорциональность | 1 | п. 6.1 в. 359 стр. 132 № 362 |
|
|
| 56 | 6.1 | Прямая пропорциональность | 1 | п. 6.1 № 364 |
|
|
| 57 | 6.2 | График функции y=kx | 1 | п. 6.2 в. 366 стр. 135 № 370, № 375 |
|
|
| 58 | 6.2 | График функции y=kx | 1 | п. 6.2 № 377, № 380 |
|
|
| 59 | 6.3 | Линейная функция и её график | 1 | п. 6.3 в. 382 стр. 140 № 386, № 390 (3 ст) |
|
|
| 60 | 6.3 | Линейная функция и её график | 1 | п. 6.3 № 394 (б, г), № 399 |
|
|
| 61 | 6.3 | Линейная функция и её график | 1 | п. 6.3 № 395, № 403; № 400 - дополнительно |
|
|
| 62 | 6.4 | Равномерное движение | 1 | п. 6.4 № 408, № 411 |
|
|
| 63 | 6.5 | Функция y=|x| и её график | 1 | п. 6.5 № 416 (б-и) |
|
|
| §7. Квадратичная функция | 9 |
|
|
|
| 64 | 7.1 | Функция y=ax2 (а0) | 1 | п. 7.1 в. 424-426 стр. 152 № 430, № 433 |
|
|
| 65 | 7.1 | Функция y=ax2 (а0) | 1 | п. 7.1 № 436, № 439 |
|
|
| 66 | 7.2 | Функция y=ax2 (а≠0) | 1 | п. 7.2 в. 443-444 стр. 156 № 447, № 448 (д-з) |
|
|
| 67 | 7.2 | Функция y=ax2 (а≠0) | 1 | п. 7.2 № 450, № 452 |
|
|
| 68 | 7.3 | График функции y=a(x-x0)2+ y0 | 1 | п. 7.3 в. 454 стр. 160 № 457, № 460 |
|
|
| 69 | 7.3 | График функции y=a(x-x0)2+ y0 | 1 | п. 7.3 № 461 (2 ст.), № 463 |
|
|
| 70 | 7.3 | График функции y=a(x-x0)2+ y0 | 1 | п. 7.3 № 471, № 467 |
|
|
| 71 | 7.4 | Квадратичная функция и её график | 1 | п. 7.4 в. 475 стр. 166 № 478 |
|
|
| 72 | 7.4 | Квадратичная функция и её график | 1 | п. 7.4 № 481, № 482 (в, г) |
|
|
| §8. Функция y=k/(x-x0)+y0 | 5 |
|
|
|
| 73 | 8.1 | Обратная пропорциональность | 1 | п. 8.1 в. 483 стр. 168 № 486, № 488 |
|
|
| 74 | 8.2 | Функция y=k/x (k0) | 1 | п. 8.2 в. 490 стр. 171 № 495, № 496 (б,в) |
|
|
| 75 | 8.3 | Функция y=k/x (k≠0) | 1 | п. 8.3 в. 497 стр. 174 № 498, № 502; № 505 - дополнительно |
|
|
| 76 | 8.4 | Дробно-линейная функция и её график | 1 | п. 8.4 № 507, № 509 (б, в) |
|
|
| 77 |
| Контрольная работа №5 по теме «Линейная и квадратичная функции» | 1 | Повторить |
|
|
| Глава IV. Системы рациональных уравнений (19 ч.) |
| §9. Системы рациональных уравнений | 10 |
|
|
|
| 78 | 9.1 | Понятие системы рациональных уравнений | 1 | п. 9.1 в. 524 стр. 194 № 527, № 531 (2ст) |
|
|
| 79 | 9.1 | Понятие системы рациональных уравнений | 1 | п. 9.1 № 533; № 536 - дополнительно |
|
|
| 80 | 9.2 | Решение систем рациональных уравнений способом подстановки | 1 | п. 9.2 в. 537 стр. 198 № 541 |
|
|
| 81 | 9.2 | Решение систем рациональных уравнений способом подстановки | 1 | п. 9.2 № 544 |
|
|
| 82 | 9.2 | Решение систем рациональных уравнений способом подстановки | 1 | п. 9.2 № 546; № 547 (2ст) - дополнительно |
|
|
| 83 | 9.3 | Решение систем рациональных уравнений другими способами | 1 | п. 9.3 № 549 |
|
|
| 84 | 9.4 | Решение задач при помощи систем рациональных уравнений | 1 | п. 9.4 № 553 |
|
|
| 85 | 9.4 | Решение задач при помощи систем рациональных уравнений | 1 | п. 9.4 № 556 |
|
|
| 86 | 9.4 | Решение задач при помощи систем рациональных уравнений | 1 | п. 9.4 № 558 |
|
|
| 87 | 9.4 | Решение задач при помощи систем рациональных уравнений | 1 | п. 9.4 № 561 |
|
|
| §10. Графический способ решения систем уравнений | 9 |
|
|
|
| 88 | 10.1 | Графический способ решения систем двух уравнений первой степени с двумя неизвестными | 1 | п. 10.1 в. 562 стр. 212 № 565 |
|
|
| 89 | 10.1 | Графический способ решения систем двух уравнений первой степени с двумя неизвестными | 1 | п. 10.1 № 566 (2 ст.) |
|
|
| 90 | 10.2 | Графический способ исследования системы двух уравнений первой степени с двумя неизвестными | 1 | п. 10.2 в. 567 стр. 216 № 574 (2 ст.), № 576 |
|
|
| 91 | 10.2 | Графический способ исследования системы двух уравнений первой степени с двумя неизвестными | 1 | п. 10.2 № 580, № 581; № 577 (2 ст.) - дополнительно |
|
|
| 92 | 10.3 | Решение систем уравнений первой и второй степени графическим способом | 1 | п. 10.3 в. 583 стр. 221 № 584 (2 ст.) |
|
|
| 93 | 10.3 | Решение систем уравнений первой и второй степени графическим способом | 1 | п. 10.3 № 585 (б, г), № 586 |
|
|
| 94 | 10.4 | Примеры решения уравнений графическим способом | 1 | п. 10.4 № 591 |
|
|
| 95 | 10.4 | Примеры решения уравнений графическим способом | 1 | п. 10.4 № 590; № 593 – дополнительно |
|
|
| 96 |
| Контрольная работа №6 по теме «Системы рациональных уравнений» | 1 | Повторить |
|
|
| Повторение | 6 |
|
|
|
| 97 |
| Функции и графики | 1 |
|
|
|
| 98 |
| Функции y=kx+b, y=ax2+bx+c, y=k/(x-x0)+y0 | 1 |
|
|
|
| 99 |
| Квадратные корни | 1 |
|
|
|
| 100 |
| Квадратные и рациональные уравнения | 1 |
|
|
|
| 101 |
| Системы рациональных уравнений | 1 |
|
|
|
| 102 |
| Итоговая контрольная работа | 1 |
|
|
|

















