Пояснительная записка
Рабочая программа по математике разработана на основе:
– Федерального закона от 29.12.2012 N 273-ФЗ "Об образовании в Российской Федерации";
– Федерального государственного стандарта среднего общего образования, утвержденного приказом Минобрнауки России от 17 мая 2012 года № 413;
– Приказа Министерства образования и науки РФ от 29 июня 2017 г. № 613 «О внесении изменений в федеральный государственный образовательный стандарт среднего общего образования, утвержденный приказом Министерства образования и науки Российской Федерации от 17 мая 2012 г. № 413»; – Постановления Главного государственного санитарного врача Российской Федерации от 29 декабря 2010 г. N189 "Об утверждении СанПиН 2.4.2.2821-10 "Санитарно-эпидемиологические требования к условиям и организации обучения в общеобразовательных учреждениях";
– Требований к результатам освоения основной образовательной программы основного общего образования Муниципального автономного общеобразовательного учреждения «Средняя общеобразовательная школа №51 г. Улан-Удэ».
Модуль «Алгебра и начала математического анализа» разработан с учётом Примерной программы среднего общего образования по математике и авторской программы: Математика: рабочие программы: 5-11 классы/ А.Г. Мерзляк, В.Б. Полонский, М.С. Якир, Е.В. Буцко. – 2-е изд. перераб. – М.: Вентана-Граф, 2017. – 164 с.
Изменения в содержание учебного материала не внесены. Программа конкретизирует содержание предметных тем образовательного стандарта: алгебра; функции; тригонометрия; начала математического анализа; уравнения и неравенства; элементы комбинаторики, статистики и теории вероятностей.
В основу программы положена концепция, предусматривающая формирование функциональных знаний и умений, которые обеспечивают целесообразное применение знаний по алгебре и началам анализа. Программа реализуется с использованием следующего учебно-методического комплекта:
10 класс
Модуль «Алгебра и начала математического анализа»
Математика. Алгебра и начала математического анализа. Базовый уровень: 10 класс: учебник / А.Г.Мерзляк, Д.А. Номировский, В.Б. Полонский; под ред. В.Е. Подольского. – 5-е изд., стереотип. – М.: Вентана-Граф, 2020. – 368 с.: ил. – (Российский учебник).
Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. Базовый уровень: 10 класс: методическое пособие / Е. В. Буцко, А. Г. Мерзляк, В. Б. Полонский, М. С. Якир. — М. : Вентана-Граф, 2020. — 113 с. : ил. — (Российский учебник).
Математика : алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. Базовый уровень : 10 класс : дидактические материалы / А. Г. Мерзляк, В. Б. Полонский, Е.М. Рабинович, М.С. Якир. — М. : Вентана-Граф, 2020 — 174 с. : ил. — (Российский учебник).
При составлении модуля «Геометрия» была использована Примерная программа среднего общего образования по математике и авторская программа: Математика: рабочие программы: 5-11 классы/ А.Г. Мерзляк, В.Б. Полонский, М.С. Якир, Е.В. Буцко. – 2-е изд. перераб. – М.: Вентана-Граф, 2017. – 164 с.
Изменения в содержание учебного материала не внесены. Программа конкретизирует содержание предметных тем образовательного стандарта: геометрия на плоскости; прямые и плоскости в пространстве; многогранники; тела вращения.
10 класс
Модуль «Геометрия»
Математика. Геометрия. Базовый уровень: 10 класс: учебник / А.Г.Мерзляк, Д.А. Номировский, В.Б. Полонский и др. – 3-е изд., стереотип. – М.: Вентана-Граф, 2020. – 208 с.: ил. – (Российский учебник).
Математика : алгебра и начала математического анализа, геометрия. Геометрия. Базовый уровень : 10 класс : методическое пособие / Е. В. Буцко, А. Г. Мерзляк, В. Б. Полонский, М. С. Якир. — М. : Вентана-Граф, 2020 — 69 с. : ил. — (Российский учебник).
Математика : алгебра и начала математического анализа, геометрия. Геометрия. Базовый уровень : 10 класс : дидактические материалы / А. Г. Мерзляк, В. Б. Полонский, Е.М. Рабинович и др.. — М. : Вентана-Граф, 2020 — 128 с. : ил. — (Российский учебник).
Согласно учебному плану на изучение математики отводится 136 часов в год: 2 часа в неделю модуль «Алгебра и начала математического анализа» и 2 часа – модуль «Геометрия»;
Срок реализации рабочей программы 1 год.
Планируемые результаты освоения учебного предмета
10 класс
Личностные результаты:
воспитание российской гражданской идентичности: патриотизма; готовности к служению Отечеству, его защите; осознания российской идентичности в поликультурном социуме; чувства причастности к историко-культурной общности российского народа и судьбе России;
мировоззрение, соответствующее современному уровню развития науки, значимости науки, готовность к научно-техническому творчеству, владение достоверной информацией о передовых достижениях и открытиях мировой и отечественной науки, заинтересованность в научных знаниях об устройстве мира и общества;
готовность и способность к саморазвитию, самообразованию и самовоспитанию в соответствии с общечеловеческими ценностями и идеалами гражданского общества;
готовность и способность к образованию, в том числе самообразованию, на протяжении всей жизни; сознательное отношение к непрерывному образованию как условию успешной профессиональной и общественной деятельности;
ориентация обучающихся на реализацию позитивных жизненных перспектив, инициативность, креативность, готовность и способность к личностному самоопределению, способность ставить цели и строить жизненные планы;
готовность к договорному регулированию отношений в группе или социальной организации; готовность обучающихся к конструктивному участию в принятии решений, затрагивающих их права и интересы, в том числе в различных формах общественной самоорганизации, самоуправления, общественно значимой деятельности;
осознанный выбор будущей профессии как путь и способ реализации собственных жизненных планов;
готовность обучающихся к трудовой профессиональной деятельности как к возможности участия в решении личных, общественных, государственных, общенациональных проблем;
нравственное сознание и поведение на основе усвоения общечеловеческих ценностей, толерантного сознания и поведения в поликультурном мире, готовности и способности вести диалог с другими людьми, достигать в нем взаимопонимания, находить общие цели и сотрудничать для их достижения;
развитие компетенций сотрудничества со сверстниками, детьми младшего возраста, взрослыми в образовательной, общественно полезной, учебно-исследовательской, проектной и других видах деятельности.
умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
представление о математической науке как сфере человеческой деятельности, об этапах её развития, о её значимости для развития цивилизации;
креативность мышления, инициатива, находчивость, активность при решении математических задач;
критичность мышления, умение распознавать логические некорректные высказывания, отличать гипотезу от факта;
умение контролировать процесс и результат учебной математической деятельности;
способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений.
Метапредметные результаты:
Регулятивные УУД:
способность самостоятельно обнаруживать и формулировать учебную проблему; определять цель учебной деятельности, задавать параметры и критерии, по которым можно определить, что цель достигнута; ставить и формулировать собственные задачи в образовательной деятельности и жизненных ситуациях; развивать мотивы и интересы своей познавательной деятельности;
оценивать возможные последствия достижения поставленной цели в деятельности, собственной жизни и жизни окружающих людей, основываясь на соображениях этики и морали;
способность самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
оценивать ресурсы, в том числе время и другие нематериальные ресурсы, необходимые для достижения поставленной цели;
организовывать эффективный поиск ресурсов, необходимых для достижения поставленной цели;
сопоставлять полученный результат деятельности с поставленной заранее целью;
умение соотносить свои действия с планируемыми результатами, определять способы действий в рамках предложенных условий и требований;
умение осуществлять контроль по образцу и вносить необходимые коррективы в соответствии с изменяющейся ситуацией;
способность адекватно оценивать правильность или ошибочность выполнения учебной задачи, её объективную трудность и собственные возможности её решения;
умение определять понятия, создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации;
умение устанавливать причинно-следственные связи; строить логические рассуждения, умозаключения (индуктивные, дедуктивные и по аналогии) и выводы;
умения создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных и познавательных задач.
Познавательные УУД:
формирование учебной и общепользовательской компетентности в области использования информационно-коммуникационных технологий (ИКТ-компетентностей);
первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;
умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
поиск и нахождение обобщенных способов решения задач, в том числе, осуществление развернутого информационного поиска и постановка на его основе новых (учебных и познавательных) задач;
критическое оценивание и интерпретирование информации с разных позиций, распознавание и фиксирование противоречия в информационных источниках;
использование различных модельно-схематических средств для представления существенных связей и отношений, а также противоречий, выявленных в информационных источниках;
нахождение и привод критических аргументов в отношении действий и суждений другого; спокойное и разумное отношение к критическим замечаниям в отношении собственного суждения, рассмотр их как ресурс собственного развития;
выход за рамки учебного предмета и осуществление целенаправленного поиска возможностей для широкого переноса средств и способов действия;
выстраивание индивидуальной образовательной траектории, с учетом ограничения со стороны других участников и ресурсные ограничения;
умение менять и удерживать разные позиции в познавательной деятельности;
умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;
умение выдвигать гипотезы при решении учебных задач и понимания необходимости их проверки;
понимание сущности алгоритмических предписаний и умения действовать в соответствии с предложенным алгоритмом;
способность планировать и осуществлять деятельность, направленную на решение задач исследовательского характера.
Коммуникативные УУД:
развитие способности осуществлять деловую коммуникацию как со сверстниками, так и со взрослыми (как внутри образовательной организации, так и за ее пределами), подбирать партнеров для деловой коммуникации исходя из соображений результативности взаимодействия, а не личных симпатий;
при осуществлении групповой работы быть как руководителем, так и членом команды в разных ролях (генератор идей, критик, исполнитель, выступающий, эксперт и т.д.);
координирование и выполнение работы в условиях реального, виртуального и комбинированного взаимодействия;
развернутое, логичное и точное изложение своей точки зрения с использованием адекватных (устных и письменных) языковых средств;
распознавание конфликтогенных ситуаций и предотвращение конфликтов до их активной фазы, выстраивание деловой и образовательной коммуникации, избегая личностных оценочных суждений.
Предметные результаты:
Учащийся научится:
Модуль «Алгебра и начала математического анализа»
осознавать значение математической науки для решения задач, возникающих в теории и в практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
осознавать значение практики и вопросов, возникающих в самой математике, для формирования и развития математической науки; историю развития понятия числа, создания математического анализа;
осознавать значение идей, методов и результатов алгебры и математического анализа для построения моделей реальных процессов и ситуаций; универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
понимать различие требований, предъявляемых к доказательствам в математике, естественных, социально–экономических и гуманитарных науках, на практике;
развивать представление о вероятностном характере различных процессов и закономерностей окружающего мира;
оперировать понятиями: отрезок, интервал, полуинтервал, промежуток с выколотой точкой, графическое представление множеств на координатной плоскости;
проводить доказательные рассуждения для обоснования истинности утверждений;
оперировать понятиями: натуральное число, множество натуральных чисел, целое число, множество целых чисел, обыкновенная дробь, десятичная дробь, смешанное число, рациональное число, множество рациональных чисел, иррациональное число, действительное число, множество действительных чисел, геометрическая интерпретация натуральных, целых, рациональных, действительных чисел;
выполнять округление рациональных и иррациональных чисел с заданной точностью;
упорядочивать числа, записанные в виде обыкновенной и десятичной дроби, числа, записанные с использованием арифметического квадратного корня;
выполнять стандартные тождественные преобразования тригонометрических, иррациональных выражений;
владеть понятиями: зависимость величин, функция, аргумент и значение функции, область определения и множество значений функции, график зависимости, график функции, нули функции, промежутки знакопостоянства, возрастание на числовом промежутке, убывание на числовом промежутке, наибольшее и наименьшее значение функции на числовом промежутке, периодическая функция, период, четная и нечетная функции; уметь применять эти понятия при решении задач;
владеть понятием обратная функция; применять это понятие при решении задач;
применять при решении задач свойства функций: четность, периодичность, ограниченность;
применять при решении задач преобразования графиков функций;
владеть понятиями числовая последовательность, арифметическая и геометрическая прогрессия;
применять при решении задач свойства и признаки арифметической и геометрической прогрессий;
владеть понятием бесконечно убывающая геометрическая прогрессия и уметь применять его при решении задач;
выполнять вычисления и преобразования выражений, содержащих действительные числа, в том числе корни натуральных степеней;
выполнять стандартные тождественные преобразования иррациональных выражений;
овладеть основными типами иррациональных, степенных уравнений и неравенств и стандартными методами их решений и применять их при решении задач;
владеть понятием степенная функция; строить ее график и уметь применять свойства степенной функции при решении задач.
переводить градусные меры углов в радианные и наоборот;
строить числовую окружность на координатной плоскости;
откладывать на числовой окружности значения различных углов;
выявлять связь между декартовыми координатами и криволинейной координатой точки на числовой окружности;
оперировать терминами: синус, косинус, тангенс, котангенс, арксинус, арккосинус, арктангенс, арккотангенс;
применять свойства синуса, косинуса, тангенса и котангенса: знаки по четвертям, сохранение значения при изменении угла на целое число оборотов, четность косинуса и нечетность синуса, тангенса и котангенса;
определять значения синуса, косинуса, тангенса и котангенса углов на числовой окружности;
работать с таблицей тригонометрических формул;
понимать сущность, запись и применение формул приведения;
владеть понятиями тригонометрические функции: 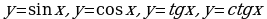 ; строить их графики и уметь применять свойства тригонометрических функций при решении задач;
; строить их графики и уметь применять свойства тригонометрических функций при решении задач;
применять формулы сложения при преобразовании тригонометрических выражений;
применять формулы двойного аргумента в работе с тригонометрическими выражениями;
применять формулы понижения степени в работе с тригонометрическими выражениями;
преобразовывать суммы тригонометрических функций в произведения;
преобразовывать произведения тригонометрических функций в суммы;
преобразовывать выражения 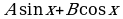 к виду
к виду  ;
;
правильно находить значения арксинусов, арккосинусов, арктангенсов и арккотангенсов чисел;
применять соответствующие формулы решения простейших тригонометрических уравнений;
выявлять среди простейших тригонометрических уравнений частные случаи;
применять к различным тригонометрическим уравнениям определенные методы их решения: введение новой переменной, разложение на множители, введение вспомогательного аргумента;
решать однородные тригонометрические уравнения различных степеней;
владеть понятиями: производная функции в точке, производная функции;
вычислять производные элементарных функций и их комбинаций;
применять правила дифференцирования функций;
пользоваться формулой вычисления производной сложной функции;
применять геометрический и физический смыслы производной на практике;
исследовать функции на монотонность и экстремумы;
строить графики и применять к решению задач, в том числе с параметром;
владеть понятием касательная к графику функции и уметь применять его при решении задач.
Учащийся получит возможность научиться:
оперировать понятием определения, основными видами определений, основными видами теорем;
понимать суть косвенного доказательства;
оперировать числовыми множествами при решении задач;
выполнять тождественные преобразования тригонометрических и иррациональных выражений;
владеть понятием асимптоты и уметь его применять при решении задач;
свободно владеть стандартным аппаратом математического анализа для вычисления производных функции одной переменной;
дифференцировать тригонометрические и обратные тригонометрические функции;
свободно применять аппарат математического анализа для исследования функций и построения графиков, в том числе исследования на выпуклость;
уметь применять при решении задач свойства непрерывных функций.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
теоретико-множественного языка и языка логики для описания реальных процессов и явлений, при решении задач других учебных предметов;
доказательных рассуждений в ситуациях повседневной жизни, при решении задач из других предметов;
записи, сравнения, округления числовых данных реальных величин с использованием разных систем измерения;
определения по графикам и использования при решения прикладных задач свойств реальных процессов и зависимостей (наибольшие и наименьшие значения, промежутки возрастания и убывания функции, промежутки знакопостоянства, асимптоты, точки перегиба, период и т.п.);
интерпретирования свойства в контексте конкретной практической ситуации;
определения по графикам простейших характеристик периодических процессов в биологии, экономике, музыке, радиосвязи и др. (амплитуда, период и т.п.);
решения прикладных задач из биологии, физики, химии, экономики и других предметов, связанных с исследованием характеристик процессов; интерпретирования полученных результатов;
практических расчетов по формулам, с использованием при необходимости справочных материалов, калькулятора, компьютера;
построения и исследования простейших математических моделей;
описания и исследования с помощью изучаемых понятий реальных зависимостей;
интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений;
решения геометрических, физических, экономических и других прикладных задач, в том числе с использованием при необходимости справочных материалов.
Модуль «Геометрия»
Учащийся научится:
понимать значение геометрии для решения задач, возникающих в теории и в практике; широту применения геометрических знаний к анализу и исследованию реальных предметов и явлений в природе и обществе;
понимать значение практики и вопросов, возникающих в самой геометрии, для формирования и развития геометрии как математической науки;
иметь представления о возможности геометрии для описания свойств реальных предметов и их взаимного расположения;
осознавать роль аксиоматики в геометрии; возможность построения геометрических теорий на аксиоматической основе; значение аксиоматики для других областей знания и для практики;
различать требования, предъявляемые к доказательствам в геометрии, алгебре, естественных, социально–экономических и гуманитарных науках, на практике;
исследовать чертежи, включая комбинации фигур, извлекать, интерпретировать и преобразовывать информацию, представленную на чертежах;
решать задачи геометрического содержания, в том числе в ситуациях, когда алгоритм решения не следует явно из условия, выполнять необходимые для решения задачи дополнительные построения, исследовать возможность применения теорем и формул для решения задач;
уметь формулировать и доказывать геометрические утверждения;
иметь представления об аксиомах стереометрии и следствиях из них и уметь применять их при решении задач;
иметь представление о скрещивающихся прямых в пространстве и уметь находить угол и расстояние между ними;
применять теоремы о параллельности прямых и плоскостей в пространстве при решении задач;
уметь применять параллельное проектирование для изображения фигур;
уметь применять перпендикулярности прямой и плоскости при решении задач;
владеть понятиями ортогональное проектирование, наклонные и их проекции, уметь применять теорему о трех перпендикулярах при решении задач;
владеть понятиями расстояние между фигурами в пространстве, общий перпендикуляр двух скрещивающихся прямых и уметь применять их при решении задач;
владеть понятием угол между прямой и плоскостью и уметь применять его при решении задач;
владеть понятиями двугранный угол, угол между плоскостями, перпендикулярные плоскости и уметь применять их при решении задач;
владеть понятиями касательные прямые и плоскости и уметь применять их при решении задач;
распознавать на чертежах и моделях прямой и наклонный параллелепипед, прямую и наклонную призмы, пирамиду, усеченную пирамиду, правильную призму и пирамиду; соотносить эти трехмерные объекты с их описаниями, изображениями;
изображать прямой и наклонный параллелепипед, прямую и наклонную призмы, пирамиду, усеченную пирамиду, правильную призму и пирамиду;
строить сечения прямого и наклонного параллелепипедов, прямой и наклонной призм, пирамиды, усеченной пирамиды, правильной призмы и пирамиды;
различать и анализировать взаимное расположение основных многогранников в пространстве;
вычислять площадь поверхности прямого и наклонного параллелепипедов;
вычислять площадь поверхности призмы;
вычислять площадь поверхности пирамиды и усеченной пирамиды;
иметь представление о теореме Эйлера, правильных многогранниках;
строить сечения многогранников с использованием различных методов, в том числе и метода следов.
Учащийся получит возможность научиться:
иметь представление об аксиоматическом методе;
владеть понятием геометрические места точек в пространстве и уметь применять их для решения задач;
уметь применять для решения задач свойства плоских и двугранных углов, трехгранного угла, теоремы косинусов и синусов для трехгранного угла;
иметь представление о площади ортогональной проекции;
иметь представление о трехгранном и многогранном угле и применять свойства плоских углов многогранного угла при решении задач;
владеть понятием перпендикулярное сечение призмы и уметь применять его при решении задач;
иметь представление о двойственности правильных многогранников;
владеть понятиями центральное и параллельное проектирование и применять их при построении сечений многогранников методом проекций;
иметь представление о развертке многогранника и кратчайшем пути на поверхности многогранника;
уметь решать задачи на плоскости методами стереометрии.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
описания реальных ситуаций на языке геометрии;
решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);
построений геометрическими инструментами (линейка, угольник, циркуль, транспортир);
составления с использованием свойств геометрических фигур математических моделей для решения задач практического характера и задач из смежных дисциплин, исследования полученных моделей и интерпретации результата.
представление о математической науке как сфере человеческой деятельности, об этапах её развития, о её значимости для развития цивилизации;
креативность мышления, инициатива, находчивость, активность при решении математических задач;
критичность мышления, умение распознавать логические некорректные высказывания, отличать гипотезу от факта;
умение контролировать процесс и результат учебной математической деятельности;
способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений.
Содержание учебного предмета
10 класс
Модуль «Алгебра и начала математического анализа»
(68 часов)
Повторение материала 7-9 классов (2 часа)
Глава 1. Повторение и расширение сведений о функции (8 часов)
Наибольшее и наименьшее значения функции. Чётные и нечётные функции. Построение графиков функций с помощью геометрических преобразований. Обратная функция. Равносильные уравнения и неравенства. Метод интервалов.
Глава 2. Степенная функция (10 часов)
Степенная функция с натуральным показателем. Степенная функция с целым показателем. Определение корня п – ой степени. Функция 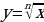 . Свойства корня п – ой степени. Определение и свойства степени с рациональным показателем. Иррациональные уравнения. Метод равносильных преобразований для решения иррациональных уравнений. Иррациональные неравенства.
. Свойства корня п – ой степени. Определение и свойства степени с рациональным показателем. Иррациональные уравнения. Метод равносильных преобразований для решения иррациональных уравнений. Иррациональные неравенства.
Глава 3: Тригонометрические функции (23 часа).
Радианная мера угла. Тригонометрические функции числового аргумента. Знаки значений тригонометрических функций. Чётность и нечётность тригонометрических функций. Периодические функции. Свойства и графики функций 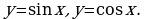 Свойства и графики функций
Свойства и графики функций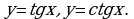 Основные соотношения между тригонометрическими функциями одного и того же аргумента. Формулы сложения. Формулы приведения. Формулы двойного и половинного углов. Сумма и разность синусов (косинусов). Формулы преобразования произведения тригонометрических функций в сумму.
Основные соотношения между тригонометрическими функциями одного и того же аргумента. Формулы сложения. Формулы приведения. Формулы двойного и половинного углов. Сумма и разность синусов (косинусов). Формулы преобразования произведения тригонометрических функций в сумму.
Глава 4: Тригонометрические уравнения и неравенства (11 часов).
Уравнение cos x=b. Уравнение sin x=b. Уравнения tg x=b и ctg x=b. Функции у=arccos x, у=arcsin x, у=arctg x и у=arcctg x. Тригонометрические уравнения, сводящиеся к алгебраическим. Решение тригонометрических уравнений методом разложения на множители. Решение простейших тригонометрических неравенств.
Глава 5: Производная и её применение (11 часов).
Представление о пределе функции в точке и о непрерывности функции в точке. Задача о мгновенной скорости и касательной к графику функции. Понятие производной, Правила вычисления производных. Уравнение касательной. Признаки возрастания и убывания функции. Точки экстремума функции. Применение производной при нахождении наибольшего и наименьшего значений функции. Построение графиков функций.
Повторение (3 часа)
Упражнения для повторения курса алгебры и начал математического анализа 10 класса.
10 класс
Модуль «Геометрия» (68 часов)
Глава 1. Введение в стереометрию (8 часов)
Основные понятия стереометрии. Аксиомы стереометрии. Следствия из аксиом стереометрии. Пространственные фигуры. Начальные представления о многогранниках. Метод сечений.
Глава 2. Параллельность в пространстве (15 часов)
Взаимное расположение двух прямых в пространстве. Параллельность прямой и плоскости. Параллельность плоскостей. Преобразования фигур в пространстве. Параллельное проектирование. Спроектируем на плоскость.
Глава 3. Перпендикулярность в пространстве (26 часов)
Угол между прямыми в пространстве. Перпендикулярность прямой и плоскости. Перпендикуляр и наклонная. Теорема о трёх перпендикулярах. Угол между прямой и плоскостью. Двугранный угол. Угол между плоскостями. Площадь ортогональной проекции многоугольника. «Стереометрическое» расположение двух прямых.
Глава 4. Многогранники (15 часов)
Призма. Параллелепипед. Пирамида. Усечённая пирамида. Платоновы тела. Геометрическое тело.
Итоговое повторение курса геометрии 10 класса (4 часа)
Аксиомы стереометрии и их следствия. Параллельность прямых и плоскостей. Перпендикулярность прямых и плоскостей. Многогранники. Площади боковых поверхностей призмы и пирамиды.
Тематическое планирование
10 класс
Модуль «Алгебра и начала математического анализа»
| № урока | Тема раздела, урока | Кол-во часов |
|
| ПОВТОРЕНИЕ МАТЕРИАЛА 7–9 КЛАССОВ | 2 |
| 1 | Упрощение выражений, содержащих квадратные корни | 1 |
| 2 | Решение уравнений. Решение неравенств | 1 |
|
| Глава 1: ПОВТОРЕНИЕ И РАСШИРЕНИЕ СВЕДЕНИЙ О ФУНКЦИИ | 8 |
| 3 | Наибольшее и наименьшее значения функции | 1 |
| 4 | Чётные и нечётные функции | 1 |
| 5 | Построение графиков функций с помощью геометрических преобразований | 1 |
| 6 | Обратная функция | 1 |
| 7 | Равносильные уравнения | 1 |
| 8 | Равносильные неравенства | 1 |
| 9 | Метод интервалов | 1 |
| 10 | Контрольная работа №1 | 1 |
|
| Глава 2: СТЕПЕННАЯ ФУНКЦИЯ | 10 |
| 11 | Степенная функция с натуральным и целым показателем | 1 |
| 12 | Определение корня n-й степени | 1 |
| 13 | Функции 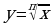 , их свойства и графики , их свойства и графики | 1 |
| 14 | Контрольная работа №2 | 1 |
| 15 | Определение и свойства степени с рациональным показателем | 1 |
| 16 | Упрощение выражений, содержащих степень с рациональным показателем | 1 |
| 17 | Иррациональные уравнения | 1 |
| 18 | Метод равносильных преобразований для решения иррациональных уравнений | 1 |
| 19 | Иррациональные неравенства | 1 |
| 20 | Контрольная работа №3 | 1 |
|
| Глава 3: ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ | 23 |
| 21 | Радианная мера угла | 1 |
| 22 | Единая окружность на координатной плоскости | 1 |
| 23 | Определение синуса, косинуса, тангенса и котангенса | 1 |
| 24 | Знаки значений тригонометрических функций | 1 |
| 25 | Чётность и нечётность тригонометрических функций | 1 |
| 26 | Периодические функции | 1 |
| 27 | Свойства и график функции y = sin x | 1 |
| 28 | Свойства и график функции y = cos x | 1 |
| 29 | Свойства и график функции y = tg x | 1 |
| 30 | Свойства и график функции y = ctg x | 1 |
| 31 | Контрольная работа №4 | 1 |
| 32 | Основные тригонометрические тождества | 1 |
| 33 | Тригонометрические функции углового аргумента | 1 |
| 34 | Синус и косинус суммы и разности аргументов | 1 |
| 35 | Тангенс суммы и разности аргументов | 1 |
| 36 | Формулы приведения | 1 |
| 37 | Формулы двойного угла | 1 |
| 38 | Формулы понижения степени | 1 |
| 39 | Упрощение тригонометрических выражений с использованием формул двойного угла и понижения степени | 1 |
| 40 | Преобразование сумм тригонометрических функций в произведения | 1 |
| 41 | Преобразование произведений тригонометрических функций в сумму | 1 |
| 42 | Закрепление преобразований произведений тригонометрических функций в сумму | 1 |
| 43 | Контрольная работа №5 | 1 |
|
| Глава 4: ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА | 11 |
| 44 | Уравнение cos x = b | 1 |
| 45 | Решение уравнений cos x = b | 1 |
| 46 | Уравнение sin x = b | 1 |
| 47 | Решение уравнений sin x = b | 1 |
| 48 | Уравнения tg x = b и ctg x = b | 1 |
| 49 | Функции y = arccos x, y = arcsin x, y = arctg x и y = arcctg x | 1 |
| 50 | Тригонометрические уравнения, сводящиеся к алгебраическим | 1 |
| 51 | Однородные тригонометрические уравнения | 1 |
| 52 | Решение тригонометрических уравнений методом введения новой переменной и методом разложения на множители | 1 |
| 53 | Решение простейших тригонометрических неравенств | 1 |
| 54 | Контрольная работа №6 | 1 |
|
| Глава 5: ПРОИЗВОДНАЯ И ЕЁ ПРИМЕНЕНИЕ | 11 |
| 55 | Представление о пределе функции в точке | 1 |
| 56 | Определение производной | 1 |
| 57 | Формулы дифференцирования | 1 |
| 58 | Дифференцирование сложной функции | 1 |
| 59 | Уравнение касательной к графику функции | 1 |
| 60 | Контрольная работа №7 | 1 |
| 61 | Применение производной для исследования функции | 1 |
| 62 | Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке | 1 |
| 63 | Исследование функции и построение графика функции | 1 |
| 64 | Связь между графиком функции и графиком производной данной функции | 1 |
| 65 | Контрольная работа №8 | 1 |
|
| ПОВТОРЕНИЕ | 3 |
| 66 | Повторение учебного материала по теме: «Преобразование тригонометрических выражений» | 1 |
| 67 | Повторение учебного материала по теме: «Производная» | 1 |
| 68 | Заключительный урок | 1 |
Модуль «Геометрия»
| № урока | Тема раздела, урока | Кол-во часов |
|
| Глава 1: ВВЕДЕНИЕ В СТЕРЕОМЕТРИЮ | 8 |
| 1 | Основные понятия стереометрии | 1 |
| 2 | Аксиомы стереометрии | 1 |
| 3 | Следствия из аксиом стереометрии | 1 |
| 4 | Применение аксиом стереометрии и их следствий | 1 |
| 5 | Пространственные фигуры | 1 |
| 6 | Начальные представления о многогранниках | 1 |
| 7 | Метод сечений | 1 |
| 8 | Контрольная работа №1 | 1 |
|
| Глава 2: ПАРАЛЛЕЛЬНОСТЬ В ПРОСТРАНСТВЕ | 15 |
| 9 | Параллельные прямые в пространстве | 1 |
| 10 | Скрещивающиеся прямые в пространстве | 1 |
| 11 | Взаимное расположение двух прямых в пространстве | 1 |
| 12 | Параллельность прямой и плоскости | 1 |
| 13 | Признаки параллельности прямой и плоскости | 1 |
| 14 | Решение задач по теме: «Параллельность прямой и плоскости» | 1 |
| 15 | Решение упражнений | 1 |
| 16 | Параллельные плоскости | 1 |
| 17 | Признак параллельности двух плоскостей | 1 |
| 18 | Свойства параллельных плоскостей | 1 |
| 19 | Преобразование фигур в пространстве | 1 |
| 20 | Виды преобразований в пространстве | 1 |
| 21 | Параллельное проектирование | 1 |
| 22 | Свойства параллельного проектирования | 1 |
| 23 | Контрольная работа №2 | 1 |
|
| Глава 3: ПЕРПЕНДИКУЛЯРНОСТЬ В ПРОСТРАНСТВЕ | 26 |
| 24 | Угол между прямыми в пространстве | 1 |
| 25 | Перпендикулярные прямые в пространстве | 1 |
| 26 | Перпендикулярность прямой и плоскости | 1 |
| 27 | Признак перпендикулярности прямой и плоскости | 1 |
| 28 | Решение задач по теме: «Перпендикулярность прямой и плоскости» | 1 |
| 29 | Перпендикуляр и наклонная | 1 |
| 30 | Расстояние от точки до плоскости | 1 |
| 31 | Расстояние от прямой до параллельной плоскости | 1 |
| 32 | Расстояние между двумя параллельными плоскости | 1 |
| 33 | Теорема о трёх перпендикулярах | 1 |
| 34 | Теорема о трех перпендикулярах | 1 |
| 35 | Решение задач по теме: «Теорема о трёх перпендикулярах» | 1 |
| 36 | Решение упражнений | 1 |
| 37 | Контрольная работа №3 | 1 |
| 38 | Угол между прямой и плоскостью | 1 |
| 39 | Решение задач по теме: «Угол между прямой и плоскостью» | 1 |
| 40 | Решение упражнений | 1 |
| 41 | Двугранный угол | 1 |
| 42 | Закрепление понятия двугранного угла | 1 |
| 43 | Угол между плоскостями | 1 |
| 44 | Решение задач по теме: «Двугранный угол» | 1 |
| 45 | Перпендикулярные плоскости | 1 |
| 46 | Признак перпендикулярности плоскостей | 1 |
| 47 | Свойства перпендикулярности плоскостей | 1 |
| 48 | Площадь ортогональной проекции многоугольника | 1 |
| 49 | Контрольная работа №4 | 1 |
|
| Глава 4: МНОГОГРАННИКИ | 15 |
| 50 | Понятие многогранника | 1 |
| 51 | Призма | 1 |
| 52 | Площадь боковой поверхности призмы | 1 |
| 53 | Решение задач по теме: «Призма» | 1 |
| 54 | Прямоугольный параллелепипед | 1 |
| 55 | Свойства диагоналей параллелепипеда | 1 |
| 56 | Теорема Пифагора в пространстве | 1 |
| 57 | Пирамида | 1 |
| 58 | Правильная пирамида | 1 |
| 59 | Площадь боковой поверхности правильной пирамиды | 1 |
| 60 | Решение задач по теме: «Пирамида» | 1 |
| 61 | Решение задач по теме: «Пирамида» | 1 |
| 62 | Усеченная пирамида | 1 |
| 63 | Площадь боковой поверхности правильной усеченной пирамиды | 1 |
| 64 | Контрольная работа №5 | 1 |
|
| ИТОГОВОЕ ПОВТОРЕНИЕ КУРСА ГЕОМЕТРИИ 10 КЛАССА | 4 |
| 65 | Повторение и систематизация учебного материала по теме: «Параллельность прямых и плоскостей» | 1 |
| 66 | Повторение и систематизация учебного материала по теме: «Перпендикулярность прямых и плоскостей» | 1 |
| 67 | Повторение и систематизация учебного материала по теме: «Площадь поверхности многогранников» | 1 |
| 68 | Обобщающий урок | 1 |
19






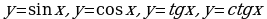 ; строить их графики и уметь применять свойства тригонометрических функций при решении задач;
; строить их графики и уметь применять свойства тригонометрических функций при решении задач;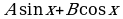 к виду
к виду 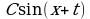 ;
;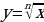 . Свойства корня п – ой степени. Определение и свойства степени с рациональным показателем. Иррациональные уравнения. Метод равносильных преобразований для решения иррациональных уравнений. Иррациональные неравенства.
. Свойства корня п – ой степени. Определение и свойства степени с рациональным показателем. Иррациональные уравнения. Метод равносильных преобразований для решения иррациональных уравнений. Иррациональные неравенства.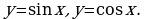 Свойства и графики функций
Свойства и графики функций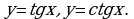 Основные соотношения между тригонометрическими функциями одного и того же аргумента. Формулы сложения. Формулы приведения. Формулы двойного и половинного углов. Сумма и разность синусов (косинусов). Формулы преобразования произведения тригонометрических функций в сумму.
Основные соотношения между тригонометрическими функциями одного и того же аргумента. Формулы сложения. Формулы приведения. Формулы двойного и половинного углов. Сумма и разность синусов (косинусов). Формулы преобразования произведения тригонометрических функций в сумму.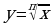 , их свойства и графики
, их свойства и графики









