А дминистрация г. Улан-Удэ
дминистрация г. Улан-Удэ
Комитет по образованию
МАОУ «Средняя общеобразовательная школа № 57 г.Улан-Удэ имени А. Цыденжапова»
РАБОЧАЯ ПРОГРАММА
| Предмет (курс, дисциплина) | Геометрия |
| Класс | 8б 8в |
| Уровень образования | Основное общее |
| Количество часов в неделю | 2 |
| ФИО учителя | Прушенова Светлана Александровна |
| Должность учителя | Учитель математики |
| Квалификационная категория | Первая |
| Срок действия программы | 1 год |
Пояснительная записка
Рабочая программа по геометрии для 8 классов составлена в соответствии с правовыми и нормативными документами:
Федеральный Закон от 29.12. 2012 г. № 273-ФЗ «Об образовании в Российской Федерации» (с изменениями);
Федеральный государственный образовательный стандарт основного общего образования, утвержденным приказом Министерства образования и науки Российской Федерации от 17.12.2010 № 1897 (далее – ФГОС основного общего образования) (в ред. Приказов Минобрнауки России от 29.12.2014 N 1644, от 31.12.2015 N 1577);
Приказ Министерства просвещения Российской Федерации от 08.05.2019 г. № 233 «О внесении изменений в федеральный перечень учебников, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования, утвержденный приказом Министерства просвещения Российской Федерации от 28.12.2018 г. № 345.
Рабочая программа составлена с учётом примерной программы основного общего образования по математике и скорректирована на её основе программа: «Геометрия 7-9» авторы Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина. Программа детализирует и раскрывает содержание стандарта, определяет общую стратегию обучения, воспитания и развития, учащихся средствами учебного предмета в соответствии с целями изучения геометрии, которые определены стандартом.
УМК: «Геометрия 7-9» авторы: Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдина, 8-е издание, М.: Просвещение, 2018 год.
Программа реализуется в объеме 68 часов из расчёта 2 часа в неделю.
Цели и задачи рабочей программы:
овладение системой математических знаний и умений, необходимых для применения практической деятельности изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как части общечеловеческой культуры, понимание значимости математики для научно -технического прогресса;
развитие представлений о полной картине мира, о взаимосвязи математики с другими предметами.
Планируемые результаты изучения предмета
Программа обеспечивает достижения следующих результатов освоения образовательной программы основного общего образования:
личностные:
формирование ответственного отношения к учению, готовности и способности обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию, выбору дальнейшего образования на базе ориентировки в мире профессий и профессиональных предпочтений, осознанному построению индивидуальной образовательной траектории с учетом устойчивых познавательных интересов;
формирование целостного мировоззрения, соответствующего современному уровню развития науки и общественной практики;
формирование коммуникативной компетентности в общении и сотрудничестве со сверстниками, старшими и младшими в образовательной, общественно полезной, учебно-исследовательской, творческой и других видах деятельности;
умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
креативность мышления, инициативу, находчивость, активность при решении геометрических задач;
умение контролировать процесс и результат учебной математической деятельности;
способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений;
метапредметные:
регулятивные универсальные учебные действия:
умение самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
умение осуществлять контроль по результату и способу действия на уровне произвольного внимания и вносить необходимые коррективы;
умение адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения;
понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;
познавательные универсальные учебные действия:
осознанное владение логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев, установления родовидовых связей;
умение устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и выводы;
умение создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных и познавательных задач;
формирование и развитие учебной и общепользовательской компетентности в области использования информационно-коммуникационных технологий (ИКТ-компетентности);
формирование первоначальных представлений об идеях и о методах математики как универсальном языке науки и техники, средстве моделирования явлений и процессов;
умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять ее в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;
умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;
умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;
коммуникативные универсальные учебные действия:
умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределять функции и роли участников, общие способы работы;
умение работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов;
слушать партнера;
формулировать, аргументировать и отстаивать свое мнение;
предметные:
Предметным результатом изучения курса является сформированность следующих умений:
пользоваться геометрическим языком для описания предметов окружающего мира;
распознавать геометрические фигуры, различать их взаимное расположение;
изображать геометрические фигуры; выполнять чертежи по условию задачи; осуществлять преобразования фигур;
распознавать на чертежах, моделях и в окружающей обстановке основные пространственные тела, изображать их;
в простейших случаях строить сечения и развертки пространственных тел;
вычислять значения геометрических величин (длин, углов, площадей); в том числе: для углов от 0 до 180° определять значения тригонометрических функций по заданным значениям углов; находить значения тригонометрических функций по значению одной из них, находить стороны, углы и вычислять площади треугольников, длины ломаных, дуг окружности, площадей основных геометрических фигур и фигур, составленных из них;
решать геометрические задачи, опираясь на изученные свойства фигур и отношений
между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, правила симметрии;
проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;
решать простейшие планиметрические задачи в пространстве.
Тематическое планирование
| № п/п | Наименование раздела | Всего часов | контроль |
| 1 | Четырехугольники | 14 | Контрольная работа №1 Самостоятельные работы-3 |
| 2 | Площадь | 14 | Контрольная работа №2 Самостоятельные работы-3 Защита проектов |
| 3 | Подобные треугольники | 19 | Контрольная работа №3 Контрольная работа №4 Самостоятельные работы-2 |
| 4 | Окружность
| 17 | Контрольная работа №5 Самостоятельные работы-3 |
| 5 | Повторение | 4 | Защита проектов |
| ИТОГО | 68 |
|
Содержание учебного предмета
| № п/п | Наименование раздела | Кол-во часов | Содержание | Планируемые результаты обучения |
| 1 | Четырехугольники | 14 | Многоугольник, выпуклый многоугольник, четырехугольник. Параллелограмм, его свойства и признаки. Трапеция. Прямоугольник, ромб, квадрат, их свойства. Осевая и центральная симметрии.
| ученик научится: - пользоваться языком геометрии для описания предметов окружающего мира и их взаимного расположения; - распознавать и изображать на чертежах и рисунках геометрические фигуры и их конфигурации; - изображать и обозначать, распознавать на чертежах выпуклые и невыпуклые многоугольники и их элементы, внешние углы многоугольника; - формулировать и объяснять определения выпуклых и невыпуклых многоугольников и их элементов; - формулировать и доказывать утверждения о сумме внешних и внутренних углов выпуклого многоугольника; - формулировать определения параллелограмма, трапеции, прямоугольной и равнобедренной трапеции и ее элементов, прямоугольника, ромба, квадрата; - изображать и обозначать, распознавать на чертежах прямоугольник, ромб, квадрат - формулировать и доказывать свойства параллелограмм; - формулировать и доказывать признаки параллелограмма; - формулировать и доказывать свойства, признаки; прямоугольной и равнобедренной трапеции, прямоугольника, ромба, квадрата; - строить симметричные точки; - распознавать фигуры, обладающие осевой и центральной симметрией. ученик получит возможность: - овладеть методикой решать задачи, применяя свойства и признаки параллелограмма, трапеции, прямоугольника, ромба, квадрата.
|
| 2 | Площадь | 14 | Понятие площади многоугольника. Площади прямоугольника, параллелограмма, треугольника, трапеции. Теорема Пифагора.
| ученик научится: - описывать ситуацию, изображенную на рисунке, соотносить чертеж и текст; -иллюстрировать и объяснять основные свойства площади, понятие равновеликости и равносоставленности; - иллюстрировать и доказывать теорему об отношении площадей треугольников, имеющих по равному углу; выводить формулы площади квадрата; -применять при решении задач на вычисления и доказательство основные свойства площадей, понятия равновеликости и равносоставленности, алгебраический аппарат; -выводить площади треугольника: традиционную и формулу Герона; - доказывать формулы площадей параллелограмма и треугольника, трапеции, ромба; – вычислять площади фигур с помощью непосредственного использования формул площадей параллелограмма и треугольника, трапеции, ромба; - находить площадь прямоугольного треугольника; --иллюстрировать и доказывать терему Пифагора - находить катет и гипотенузу в прямоугольном треугольнике с помощью теоремы Пифагора. ученик получит возможность: -применять изученные формулы для нахождения площадей для решения задач; -применять при решении задач на вычисление площадей метод площадей, теорему, теорему, обратную теореме Пифагора; -применять при решении задач на вычисления и доказательство метод площадей. |
| 3 | Подобные треугольники | 19 | Подобные треугольники. Признаки подобия треугольников. Применение подобия к доказательству теорем и решению задач. Синус, косинус и тангенс острого угла прямоугольного треугольника.
| ученик научится: объяснять понятия: подобия, коэффициента подобия, подобных треугольников, пропорциональных отрезков; - изображать и обозначать, распознавать на чертежах подобные треугольники, средние линии треугольников, выделять в конфигурации, данной в условии задачи подобные треугольники, средние линии треугольников, -формулировать и иллюстрировать, доказывать теорему об отношении площадей подобных треугольников; -формулировать и иллюстрировать, доказывать признаки подобия треугольников; -формулировать и иллюстрировать, доказывать теорему о средней линии треугольника; - формулировать и иллюстрировать понятие пропорциональных отрезков, - формулировать и иллюстрировать свойство биссектрисы угла треугольника; - формулировать и иллюстрировать, доказывать теорему о пропорциональных отрезках в прямоугольном треугольнике -формулировать и иллюстрировать, доказывать теорему о точке пересечения медиан треугольника; -объяснять тригонометрические термины «синус», «косинус», «тангенс», оперировать начальными понятиями тригонометрии; -решать прямоугольные треугольники; -применять при решении задач на вычисления: признаки подобия треугольников, теорему о средней линии треугольника, теорем о пропорциональных отрезках в прямоугольном треугольнике (понятие среднего геометрического двух отрезков, свойство высоты в прямоугольном треугольнике, проведенной из вершины прямого угла, свойство катетов прямоугольного треугольника, определений тригонометрических функций острого угла в прямоугольном треугольнике; ученик получит возможность: - применять признаки подобия треугольников при решении задач; - применять подобие треугольников в измерительных работах на местности; - применять теоремы о подобных треугольниках при решении задач на построение; - применять основные тригонометрические тождества в процессе решения задач; - применять при решении задач на построение понятие подобия. |
| 4 | Окружность | 17 | Взаимное расположение прямой и окружности. Касательная к окружности, ее свойство и признак. Центральные и вписанные углы. Четыре замечательные точки треугольника. Вписанная и описанная окружности.
| ученик научится: - изображать и обозначать, распознавать на чертежах вписанные и описанные окружности, касательные к окружности, центральные и вписанные углы; -выделять в конфигурации вписанные и описанные окружности, касательные к окружности, центральные и вписанные углы; -формулировать и иллюстрировать определения вписанных и описанных окружностей, касательной к окружности, центральных и вписанных углов; - формулировать и иллюстрировать, доказывать теорему о признаке и свойстве касательной к окружности; - формулировать и иллюстрировать, доказывать теорему о вписанном угле, следствия из этой теоремы; - формулировать и иллюстрировать, доказывать теорему о свойстве отрезков касательных, проведенных из одной точки, о свойстве отрезков пересекающихся хорд; - формулировать и иллюстрировать, доказывать теорему о вписанных в треугольник и описанных около треугольника окружностях и следствия из них; - формулировать и иллюстрировать, доказывать теорему о свойствах вписанных в окружность и описанных около окружности многоугольниках; -устанавливать взаимное расположение прямой и окружности - применять при решении задач на вычисление и доказательство: теоремы о вписанном угле, следствия из этой теоремы, теоремы о свойстве касательной к окружности, о свойстве отрезков касательных, проведенных из одной точки, о свойстве отрезков пересекающихся хорд ученик получит возможность: - решать задачи с использованием замечательных точек треугольника; - решать задачи на нахождение углов в окружности; -применять метод геометрического места точек для решения задач и для доказательства. |
| 5 | Повторение | 4 | Повторение. Решение задач | ученик научится: - решать планиметрические задачи ученик получит возможность: -систематизировать полученные знания; - применять полученные знания на практике, логически мыслить, отстаивать свою точку зрения и выслушивать мнение других, работать в команде. |
|
|
| 68 ч |
|
|
Система оценки планируемых результатов
Одним из направлений оценочной деятельности в соответствии с требованиями Стандарта является оценка образовательных достижений учащихся.
Система оценки достижения планируемых результатов по алгебре направлена на обеспечение качества математического образования. Она должна позволять отслеживать индивидуальную динамику развития учащихся, обеспечивать обратную связь для учителей и, учащихся и родителей.
Формирование личностных результатов обеспечивается в ходе реализации всех компонентов образовательного процесса, включая внеурочную деятельность, реализуемую семьёй и школой.
Основным объектом оценки личностных результатов служит сформированность универсальных учебных действий, включаемых в следующие три основных блока:
Сформированность основ гражданской идентичности личности;
Готовность к переходу к самообразованию на основе учебно-познавательной мотивации, в том числе готовность к выбору направления профильного образования;
Сформированность социальных компетенций, включая ценностно-смысловые установки и моральные нормы, опыт социальных и межличностных отношений, правосознание.
Основным объектом оценки метапредметных результатов является:
Способность и готовность к освоению систематических знаний по алгебре, их самостоятельному пополнению, переносу и интеграции;
Способность к сотрудничеству и коммуникации в ходе учебной и внеучебной деятельности;
Способность и готовность к использованию ИКТ в целях обучения и развития;
Способность к самоорганизации, саморегуляции и рефлексии.
Основным объектом оценки предметных результатов по алгебре в соответствии с требованиями Стандарта является способность к решению учебно-познавательных и учебно-практических задач, основанных на изучаемом учебном материале, с использованием способов действий, релевантных содержанию учебных предметов, в том числе метапредметных (познавательных, регулятивных, коммуникативных) действий.
Основными видами оценивания образовательных достижений по математике являются стартовое. Текущее и итоговое.
Стартовое оценивание позволяет спланировать личностно-ориентированное обучение, индивидуализировать образовательный процесс.
Текущее оценивание позволяет определить уровень усвоения нового материала. Степень самостоятельности учащихся при решении задач, характер применения рациональных способов решения задач и др. Для текущего оценивания используются следующие методы контроля.
Устный контроль: фронтальный опрос, индивидуальный опрос;
Письменный контроль: математический диктант, самостоятельная работа, контрольная работа, реферат, тест;
Практический контроль: фронтальная или индивидуальная практическая работа, домашняя контрольная работа, исследовательская работа, проектная работа.
Итоговое оценивание может проводиться после завершения темы, раздела, учебного курса основной или старшей школы (в частности, в виде итоговой аттестации). Итоговая оценка результатов освоения учащимися основной образовательной программы выставляется по результатам промежуточной и итоговой аттестации и формируется на основе:
Результатов внутришкольного мониторинга образовательных достижений по алгебре, зафиксированных в оценочных листах, в том числе за промежуточные и итоговые работы на мепредметной основе;
Оценок за выполнение итоговых работ по алгебре;
Оценки за выполнение и защиту индивидуального проекта;
Оценок за работы, выносимые на государственную итоговую аттестацию (ГИА) и единый государственный экзамен (ЕГЭ).
Особенности оценки предметных результатов
Оценка предметных результатов представляет собой оценку достижения обучающимся планируемых результатов по отдельным предметам.
Формирование этих результатов обеспечивается за счёт основных компонентов образовательного процесса — учебных предметов.
Основным объектом оценки предметных результатов в соответствии с требованиями Стандарта является способность к решению учебно-познавательных и учебно-практических задач, основанных на изучаемом учебном материале, с использованием способов действий, релевантных содержанию учебных предметов, в том числе метапредметных (познавательных, регулятивных, коммуникативных) действий.
Система оценки предметных результатов освоения учебных программ с учётом уровневого подхода, принятого в Стандарте, предполагает выделение базового уровня достижений как точки отсчёта при построении всей системы оценки и организации индивидуальной работы с обучающимися.
Реальные достижения обучающихся могут соответствовать базовому уровню, а могут отличаться от него как в сторону превышения, так и в сторону недостижения.
Практика показывает, что для описания достижений обучающихся целесообразно установить следующие пять уровней.
Базовый уровень достижений — уровень, который демонстрирует освоение учебных действий с опорной системой знаний в рамках диапазона (круга) выделенных задач. Овладение базовым уровнем является достаточным для продолжения обучения на следующей ступени образования, но не по профильному направлению. Достижению базового уровня соответствует отметка «удовлетворительно» (или отметка «3», отметка «зачтено»).
Превышение базового уровня свидетельствует об усвоении опорной системы знаний на уровне осознанного произвольного овладения учебными действиями, а также о кругозоре, широте (или избирательности) интересов. Целесообразно выделить следующие два уровня, превышающие базовый:
повышенный уровень достижения планируемых результатов, оценка «хорошо» (отметка «4»);
высокий уровень достижения планируемых результатов, оценка «отлично» (отметка «5»).
Повышенный и высокий уровни достижения отличаются по полноте освоения планируемых результатов, уровню овладения учебными действиями и сформированностью интересов к данной предметной области.
Индивидуальные траектории обучения обучающихся, демонстрирующих повышенный и высокий уровни достижений, целесообразно формировать с учётом интересов этих обучающихся и их планов на будущее. При наличии устойчивых интересов к учебному предмету и основательной подготовки по нему такие обучающиеся могут быть вовлечены в проектную деятельность по предмету и сориентированы на продолжение обучения в старших классах по данному профилю.
Для описания подготовки учащихся, уровень достижений которых ниже базового, целесообразно выделить также два уровня:
пониженный уровень достижений, оценка «неудовлетворительно» (отметка «2»);
низкий уровень достижений, оценка «плохо» (отметка «1»).
Недостижение базового уровня (пониженный и низкий уровни достижений) фиксируется в зависимости от объёма и уровня освоенного и неосвоенного содержания предмета.
Как правило, пониженный уровень достижений свидетельствует об отсутствии систематической базовой подготовки, о том, что обучающимся не освоено даже и половины планируемых результатов, которые осваивает большинство обучающихся, о том, что имеются значительные пробелы в знаниях, дальнейшее обучение затруднено. При этом обучающийся может выполнять отдельные задания повышенного уровня. Данная группа обучающихся (в среднем в ходе обучения составляющая около 10%) требует специальной диагностики затруднений в обучении, пробелов в системе знаний и оказании целенаправленной помощи в достижении базового уровня.
Низкий уровень освоения планируемых результатов свидетельствует о наличии только отдельных фрагментарных знаний по предмету, дальнейшее обучение практически невозможно. Обучающимся, которые демонстрируют низкий уровень достижений, требуется специальная помощь не только по учебному предмету, но и по формированию мотивации к обучению, развитию интереса к изучаемой предметной области, пониманию значимости предмета для жизни и др. Только наличие положительной мотивации может стать основой ликвидации пробелов в обучении для данной группы обучающихся.
Критерии и нормы оценки знаний, умений и навыков обучающихся по математике.
1. Оценка письменных контрольных работ обучающихся по математике.
Отметка «5», если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Отметка «1» ставится, если:
работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
2. Оценка устных ответов обучающихся по математике
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке обучающихся» в настоящей программе по математике);
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме; при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Отметка «1» ставится, если:
ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изученному материалу.
Общая классификация ошибок
При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.
Грубыми считаются ошибки:
незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
незнание наименований единиц измерения;
неумение выделить в ответе главное;
неумение применять знания, алгоритмы для решения задач;
неумение делать выводы и обобщения;
неумение читать и строить графики;
неумение пользоваться первоисточниками, учебником и справочниками;
потеря корня или сохранение постороннего корня;
отбрасывание без объяснений одного из них;
равнозначные им ошибки;
вычислительные ошибки, если они не являются опиской;
логические ошибки.
К негрубым ошибкам следует отнести:
неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного — двух из этих признаков второстепенными;
неточность графика;
нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
нерациональные методы работы со справочной и другой литературой;
неумение решать задачи, выполнять задания в общем виде.
Недочетами являются:
нерациональные приемы вычислений и преобразований;
небрежное выполнение записей, чертежей, схем, графиков.
Контроль ЗУН предлагается при проведении математических диктантов, практических работ, самостоятельных работ обучающего и контролирующего вида, контрольных работ.
Контрольно- измерительные материалы
| Входная диагностика. | 1 вариант | 2 вариант. | | 1). В равнобедренном треугольнике АВС с основанием АС угол В равен 42 0. Найдите два других угла треугольника АВС.
2). Величины смежных углов пропорциональны числам 5 и 7. Найдите разность между этими углами.
3). В прямоугольном треугольнике АВС 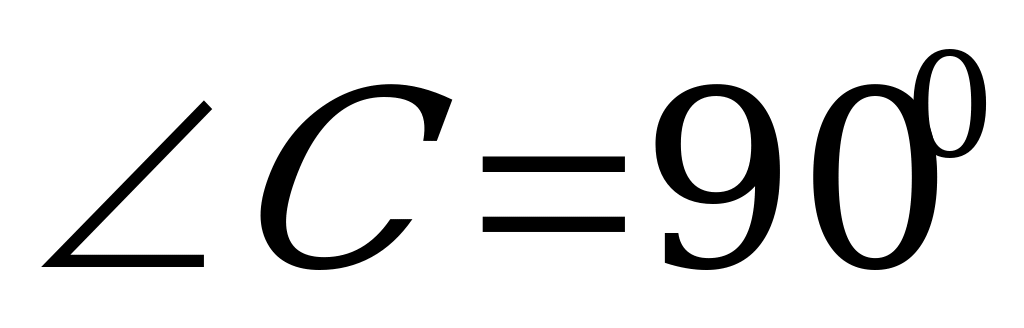 , , 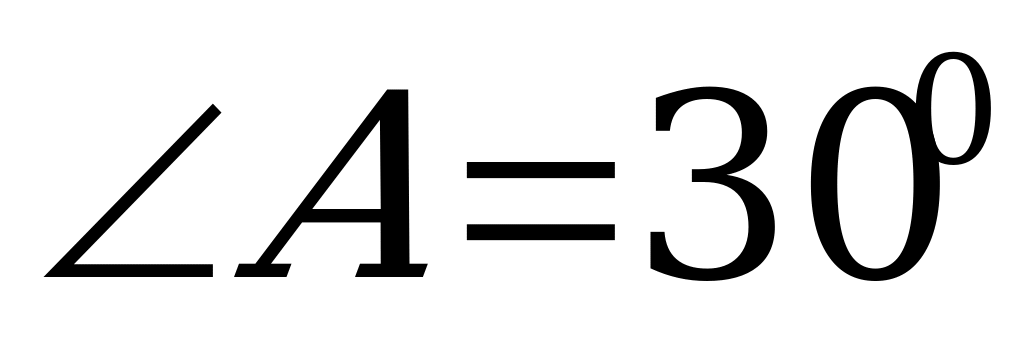 , АС = 10 см , СD , АС = 10 см , СD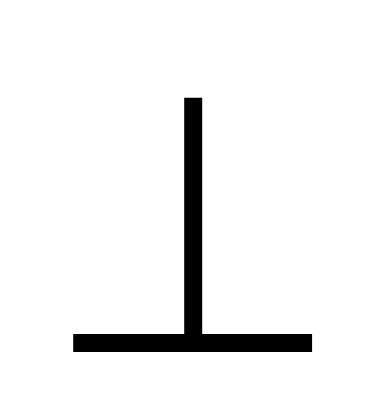 АВ, DE АВ, DE 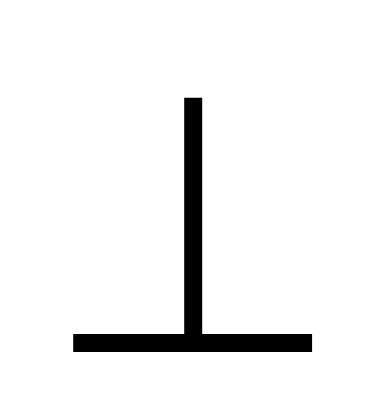 АС. Найдите АЕ. АС. Найдите АЕ.
4). В треугольнике МРК угол Р составляет 60 0углаК, а угол М на 40 больше угла Р. Найдите угол Р. | 1). В равнобедренном треугольнике АВС с основанием АС сумма углов А и С равна 1560. Найдите углы треугольника АВС.
2). Величины смежных углов пропорциональны числам 4 и 11. Найдите разность между этими углами.
3). В прямоугольном треугольнике АВС 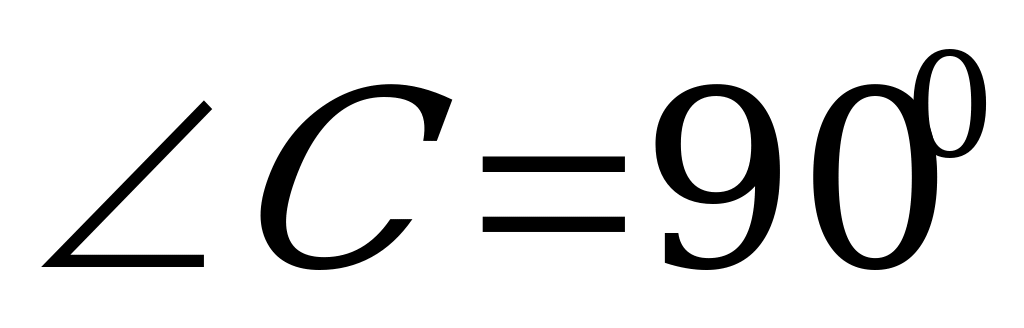 , , 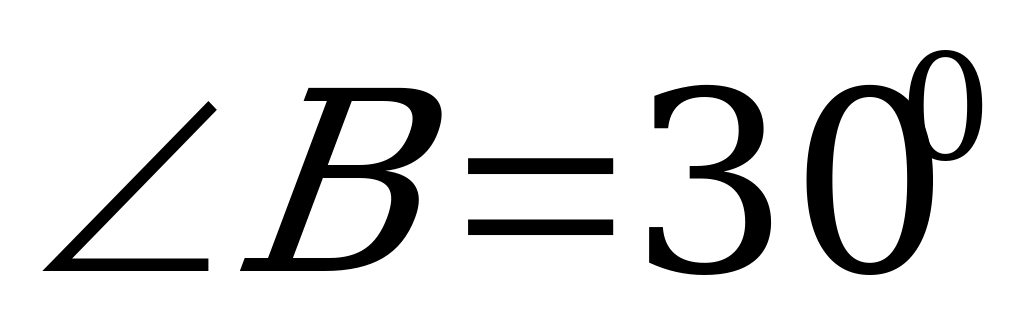 , ВС = 18 см , СК , ВС = 18 см , СК 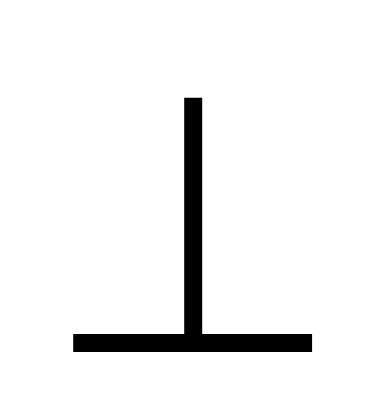 АВ, КМ АВ, КМ 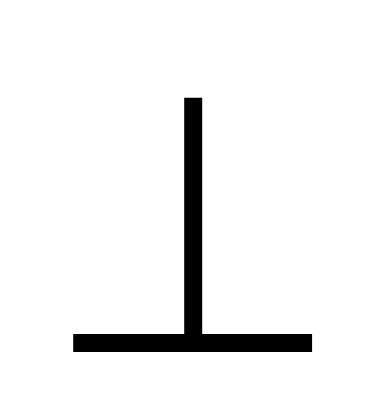 ВС. Найдите МВ. ВС. Найдите МВ.
4). В треугольнике BDE угол В составляет 30 0 угла D, а угол Е на 19 0больше угла D. Найдите угол В.
|
|
Контрольная работа №1
Тема: «Четырёхугольники»
Вариант – 1
1) Диагонали прямоугольника АВСД пересекаются в точке О. Найдите угол между диагоналями, если угол АВО = 30º.
2) В параллелограмме КМNР проведена биссектриса угла МКР, которая пересекает сторону МN в точке Е.
а) Докажите, что треугольник КМЕ равнобедренный.
б) Найдите сторону КР, если МЕ = 10 см, а периметр параллелограмма равен 52 см.
Вариант – 2
1) Диагонали ромба КМNР пересекаются в точке О. Найдите углы треугольника КОМ, если угол МNР= 80º
2) На стороне ВС параллелограмма АВСД взята точка М так, что АВ = ВМ.
а) Докажите, что АМ – биссектриса угла ВАД.
б) Найдите периметр параллелограмма, если СД = 8 см, СМ = 4 см.
Контрольная работа №2
Тема: «Площадь»
Вариант – 1
1) Смежные стороны параллелограмма равны 32 см и 26 см, а один из его углов равен 150º. Найдите площадь параллелограмма.
2) Сторона треугольника равна 5 см, а высота, проведённая к ней, в два раза больше стороны. Найдите площадь треугольника.
3) Катеты прямоугольного треугольника равны 6 и 8 см. Найдите гипотенузу и площадь треугольника.
4) Найдите площадь и периметр ромба, если его диагонали равны 8 и 10 см.
5) Площадь прямоугольной трапеции равна120 см², а её высота равна 8 см. Найдите все стороны трапеции, если одно из оснований больше другого на 6 см.
Вариант – 2
1) Одна из диагоналей параллелограмма является его высотой и равна 9 см. Найдите стороны параллелограмма, если его площадь равна 108 см².
2) Сторона треугольника равна 12 см, а высота, проведённая к ней, в три раза меньше. Найдите площадь треугольника.
3) Один из катетов прямоугольного треугольника равен 12 см, а гипотенуза 13 см. Найдите второй катет и площадь прямоугольного треугольника.
4) Диагонали ромба равны 10 и 12 см. Найдите его площадь и периметр.
5) Найдите площадь трапеции АВСД с основаниями АД и ВС, если АВ = 12 см, ВС = 14 см, АД = 30 см, угол В равен 150º.
Контрольная работа №3
Тема: «Подобные треугольники»
Вариант – 1
1

 ) На рисунке АВ ║СД. А В
) На рисунке АВ ║СД. А В
а) Докажите, что АО : ОС = ВО : ОД.
б) Найдите АВ, если ОД = 15 см, ОВ = 9 см, СД = 25 см.
Д С
2) Найдите отношение площадей треугольников АВС и КМN, если АВ =8 см, ВС=12 см, АС= 16 см, МN=15 см, NК=20 см.
В
 Вариант – 2
Вариант – 2
1 ) На рисунке МN ║АС. MN
) На рисунке МN ║АС. MN
а) Докажите, что АВ ∙ ВN = СВ ∙ ВМ. AC
б) Найдите МN, если АМ=6 см, ВМ=8 см, АС=21 см
2) Даны стороны треугольника РQR и АВС: РQ=16 см, QR=20 см, РR=28 см и АВ=12 см, ВС=15 см, АС=21см.
Найдите отношение площадей этих треугольников.
Контрольная работа №4
Тема: «Соотношение между сторонами и углами прямоугольного треугольника»
Вариант – 1
1) В прямоугольном треугольнике АВС угол А= 90º, АВ=20 см, высота АД равна 12 см. Найдите АC и cosC.
2) Диагональ ВД параллелограмма АВСД перпендикулярна к стороне АД. Найдите площадь параллелограмма АВСД, если АВ=12 см, угол А=41º.
Вариант – 2
1) Высота ВД прямоугольного треугольника АВС равна 24 см и отсекает от гипотенузы АС отрезок ДС, равный 18 см. Найдите АВ и cosA.
2) Диагональ АС прямоугольника АВСД равна 3 см и составляет со стороной АД угол в 37º. Найдите площадь прямоугольника АВСД.
Контрольная работа №5
Тема: «Окружность»
Вариант – 1
1) Через точку А окружности проведены диаметр АС и две хорды АВ и АД, равные радиусу этой окружности. Найдите углы четырёхугольника АВСД и градусные меры дуг АВ, ВС, СД, АД.
2) Основание равнобедренного треугольника равно 18 см, а боковая сторона равна 15 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей.
Вариант – 2
1) Отрезок ВД – диаметр окружности с центром О. Хорда АС делит пополам радиус ОВ и перпендикулярна к нему. Найдите углы четырёхугольника АВСД и градусные меры дуг АВ, ВС, СД, АД.
2) Высота, проведённая к основанию равнобедренного треугольника, равна 9 см, а само основание равно 24 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей.
Итоговая контрольная работа по геометрии 8 класс
1 вариант
1. Найдите площадь равнобедренного треугольника со сторонами 10см, 10см и 12 см.
2. В параллелограмме две стороны 12 и 16 см, а один из углов 150°. Найдите площадь параллелограмма.
3. В равнобедренной трапеции боковая сторона равна 13 см, основания 10 см и 20 см. Найдите площадь трапеции.
4. В треугольнике АВС прямая MN , параллельная стороне АС, делит сторону ВС на отрезкиBN=15 см и NC=5 см, а сторону АВ на ВМ и АМ. Найдите длину отрезка MN, если АС=15 см.
5. В прямоугольном треугольнике АВС  =90°, АС=8 см,
=90°, АС=8 см,  =45°. Найдите:
=45°. Найдите:
а)АС; б) высоту СD, проведенную к гипотенузе.
6. Дан прямоугольный треугольник АВС, у которого  С-прямой, катет ВС=6 см и
С-прямой, катет ВС=6 см и  А=60°. Найдите:
А=60°. Найдите:
а) остальные стороны ∆АВС
б) площадь ∆АВС
в) длину высоты, опущенной из вершины С.
2 вариант
1. В равнобедренном треугольнике боковая сторона равна 13 см, а высота, проведенная к основанию, 5 см. Найдите площадь этого треугольника.
2. В параллелограмме АВСД АВ=8 см, АД=10 см,  =30°. Найдите площадь параллелограмма.
=30°. Найдите площадь параллелограмма.
3. В прямоугольной трапеции АВСД боковая сторона равна АВ=10 см, большее основание АД= 18 см,  =45°. Найдите площадь трапеции.
=45°. Найдите площадь трапеции.
4. В треугольнике АВС со сторонами АС=12 см и АВ=18 см проведена прямая MN, параллельная АС, MN=9 см. Найдите ВМ.
5. В прямоугольном треугольнике АВС  =90°, АС=8 см,
=90°, АС=8 см,  =45° . Найдите:
=45° . Найдите:
а)АВ; б) высоту СD, проведенную к гипотенузе.
6. Дан прямоугольный треугольник АDС, у которого  D-прямой, катет AD=3 см и
D-прямой, катет AD=3 см и  DАC=30°. Найдите:
DАC=30°. Найдите:
а) остальные стороны ∆АDС
б) площадь ∆АDС
в) длину высоты, проведенной к гипотенузе.
КОМПЛЕКТ ТЕОРЕТИЧЕСКИХ ВОПРОСОВ НА КОНЕЦ ГОДА
| 1 | Объясните, какая фигура называется многоугольником. Назовите элементы многоугольника. |
| 2 | Какой многоугольник называется выпуклым? |
| 3 | Выведите формулу для вычисления суммы углов выпуклого n-угольника. |
| 4 | Чему равна сумма углов выпуклого четырехугольника? |
| 5 | Дайте определение параллелограмма, ромба, прямоугольника, трапеции, квадрата. |
| 6 | Сформулируйте и докажите свойства параллелограмма. |
| 7 | Сформулируйте и докажите признаки параллелограмма. |
| 8 | Сформулируйте и докажите свойство прямоугольника. |
| 9 | Сформулируйте и докажите свойств диагоналей ромба. |
| 10 | Сформулируйте и докажите свойства квадрата. |
| 11 | Введите понятия осевой и центральной симметрии. Приведите примеры фигур, обладающих осевой и центральной симметрией. |
| 12 | Расскажите, как измеряются площади многоугольников. |
| 13 | Сформулируйте основные свойства площадей многоугольников. |
| 14 | Сформулируйте и докажите теорему о вычислении площади прямоугольника. |
| 15 | Сформулируйте и докажите теорему о вычислении площади треугольника. Как вычислить площадь прямоугольного треугольника. |
| 16 | Сформулируйте и докажите теорему об отношении площадей треугольников, имеющих равные углы.. |
| 17 | Сформулируйте и докажите теорему о вычислении площади трапеции. |
| 18 | Сформулируйте и докажите теорему о вычислении площади ромба. |
| 19 | Сформулируйте и докажите теорему Пифагора и обратную ей теорему. |
| 20 | Дайте определение подобных треугольников. |
| 21 | Сформулируйте и докажите теорему об отношении площадей подобных треугольников. |
| 22 | Сформулируйте и докажите признаки подобия треугольников. |
| 23 | Какой отрезок называется средней линией треугольника. Сформулируйте и докажите теорему о средней линии треугольника. |
| 24 | Сформулируйте и докажите утверждение о точке пересечения медиан треугольника. |
| 25 | Сформулируйте и докажите утверждения о пропорциональных отрезках в прямоугольном треугольнике. |
| 26 | Что такое коэффициент подобия? |
| 27 | Что называется синусом, косинусом, тангенсом острого угла прямоугольного треугольника? |
| 28 | Какое равенство называется основным тригонометрическим тождеством? |
| 29 | Чему равны значения синуса, косинуса и тангенса для углов 300, 450, 600? |
| 30 | Сформулируйте выводы о взаимном расположении окружности прямой. |
| 31 | Какая прямая называется секущей по отношению к окружности? |
| 32 | Какая прямая называется касательной к окружности? Как называется общая точка прямой и окружности? |
| 33 | Сформулируйте и докажите теорему о свойстве касательной к окружности и обратную теорему. |
| 34 | Докажите утверждение об отрезках касательных к окружности, проведенных из одной точки. |
| 35 | Какой угол называется центральным углом? вписанным углом? |
| 36 | Как определяется градусная мера дуги? |
| 37 | Как определяется градусная мера центрального и вписанного угла? |
| 38 | Сформулируйте теоремы о четырех замечательных точках треугольника. |
| 39 | Какая окружность называется вписанной в многоугольник? описанной около многоугольника? |
| 40 | Какой многоугольник называется вписанным в окружность? описанным около окружности? |
| 41 | Сформулируйте теоремы о вписанной в треугольник и описанной около треугольника окружностях. |
| 42 | Каким свойством обладают стороны четырехугольника, описанного около окружности? вписанного в окружность? |
5






 дминистрация г. Улан-Удэ
дминистрация г. Улан-Удэ

 ) На рисунке АВ ║СД. А В
) На рисунке АВ ║СД. А В Вариант – 2
Вариант – 2 ) На рисунке МN ║АС. MN
) На рисунке МN ║АС. MN =90°, АС=8 см,
=90°, АС=8 см,  =45°. Найдите:
=45°. Найдите: С-прямой, катет ВС=6 см и
С-прямой, катет ВС=6 см и  =45°. Найдите площадь трапеции.
=45°. Найдите площадь трапеции.









