© 2020 283 0


СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Рабочая программа учебного предмета «Алгебра» для 8 класса
Рабочая программа учебного предмета «Алгебра» для 8 класса разработана по ФГОС СОО на основе авторской программы: Математика: программы: 5-11 классы / (А.Г. Мерзляк, В.Б. Полонский, М.С. Якир и др.). — М.: Вентана-Граф,2017.-152с. Расчитана на 102 часа из расчета 3 часа в неделю (34 недели).
Просмотр содержимого документа
«Рабочая программа учебного предмета «Алгебра» для 8 класса»
Муниципальное общеобразовательное учреждение «МОУ Гимназия №1»
Принято
педагогическим советом
МОУ «Гимназия №1»
Протокол № __ от «__» августа 2016 г.
Утверждена
приказом №____
от «____» августа 2016 г.
Директор МОУ «Гимназия №1»
____________/Т.Г. Андреева
Рабочая программа
учебного предмета
«Математика»
(алгебра)
основное общее образование
8 класс
(базовый уровень)
на 2016-2017 учебный год
Составитель: учитель математики
Агашкова Надежда Анатольевна
г. Железногорск
2016 г.
I. Пояснительная записка
Рабочая программа учебного предмета «Алгебра» для 8 класса разработана на основе следующих документов:
Закона РФ «Об образовании в Российской Федерации» №273-ФЗ от 29.12.2012г;
Федеральный государственный образовательный стандарт основного общего образования / Министерство образования и науки РФ. – М.: Просвещение, 2011(Стандарты второго поколения) Приказ Министерства образования и науки РФ от 17.12.2010 № 1897;
Примерной программы по учебным предметам «Математика 5 – 9 класс» – М.: Просвещение, 2015 г
авторской программы: Программы. Математика. 5-6 классы. Алгебра 7-9 классы. Алгебра и начала математического анализа. 10-11 классы (базовый уровень) / авт.-сост. И.И. Зубарева, А.Г. Мордкович. – 2-е изд., испр. и доп. – М.: Мнемозина, 2009. – 63 с.;
федерального перечня учебников, рекомендуемых Министерством образования РФ к использованию в образовательном процессе в образовательных учреждениях на 2016-2017 учебный год;
федерального базисного учебного плана;
регионального учебного плана;
учебного плана гимназии.
В данных документах учитываются основные идеи и положения Программы развития и формирования универсальных учебных действий для основного общего образования.
Общая характеристика учебного предмета
Школьное образование в современных условиях призвано обеспечить функциональную грамотность и социальную адаптацию обучающихся на основе приобретения ими компетентностного опыта в сфере учения, познания, профессионально-трудового выбора, личностного развития, ценностных ориентаций и смыслотворчества. Это предопределяет направленность целей обучения на формирование компетентной личности, способной к жизнедеятельности и самоопределению в информационном обществе, ясно представляющей свои потенциальные возможности, ресурсы и способы реализации выбранного жизненного пути.
Курс математики в 8 классе складывается из следующих содержательных компонентов: арифметика (на уроках повторения и обобщения); алгебра; геометрия; элементы комбинаторики, теории вероятностей, статистики и логики. В своей совокупности они отражают богатый опыт обучения математике в нашей стране, учитывают современные тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационно емком и практически значимом материале. Эти содержательные компоненты, развиваясь на протяжении всех лет обучения, естественным образом переплетаются и взаимодействуют в учебных курсах.
Курс математики характеризуется повышением теоретического уровня обучения, постепенным усилением роли теоретических обобщений и дедуктивных заключений. Прикладная направленность курса обеспечивается систематическим обращением к примерам, раскрывающим возможности применения математики к изучению действительности и решению практических задач.
Арифметика призвана способствовать приобретению практических навыков, необходимых для повседневной жизни. Она служит базой для всего дальнейшего изучения математики, способствует логическому развитию и формированию умения пользоваться алгоритмами.
Алгебра нацелена на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира. Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры.
Целью изучения курса алгебры 8 класса является развитие вычислительных и формально – оперативных алгебраических умений до уровня, позволяющего уверенно использовать их при решении задач математики и смежных предметов, усвоение аппарата уравнений и неравенств как основного средства математического моделирования прикладных задач, осуществление функциональной подготовки школьников.
Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования представлений о роли математики в развитии цивилизации и культуры.
Элементы логики, комбинаторики, статистики и теории вероятностей становятся обязательным компонентом школьного образования, усиливающим его прикладное и практическое значение. Этот материал необходим для формирования функциональной грамотности – умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчеты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчёт числа вариантов, в том числе и простейших прикладных задач. При изучении статистики и теории вероятностей обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации и закладываются основы вероятностного мышления.
Курс алгебры построен в соответствии с традиционными содержательно-методическими линиями: числовой, функциональной, алгоритмической, уравнений и неравенств, алгебраических преобразований.
Одной из главных особенностей курса алгебры является то, что в нем реализуется взаимосвязь принципов научности и доступности и уделяется особое внимание обеспечению прочного усвоения основ математических знаний всеми учащимися.
Особенностью курса является также его практическая направленность, которая служит стимулом развития у учащихся интереса к алгебре, а также основной для формирования осознанных математических навыков и умений.
«Идеология» основного курса алгебры делает его органическим продолжением и обобщением курса арифметики. Центральное понятие этого курса – понятие числа – развивается и расширяется от рационального до действительного. Усвоение алгебры осуществляется успешно, если изучение теоретического материала проходит в процессе решения задач. Этим достигается осмысленность и прочность знаний учащихся.
Большое количество разнообразных задач на применение алгебры в геометрии, физике, технике и т.д. помогает учащимся понять практическую необходимость изучения алгебры.
В ходе преподавания алгебры в 8 классе, работы над формированием у учащихся универсальных учебных действий следует обращать внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:
• планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;
• решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;
• исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки
и формулирования новых задач;
• ясного, точного, грамотного изложения своих мыслей в устной и письменной форме, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;
• проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;
• поиска, систематизации, анализа и классификации информации, использования разнообразных
информационных источников, включая учебную и справочную литературу, современные информационные технологии.
Цели и задачи изучения алгебры
На основании требований Государственного образовательного стандарта в содержании предполагается реализовать актуальные в настоящее время компетентностный, личностно ориентированный, деятельностный подходы, которые определяют задачи обучения:
Выработать умение выполнять тождественные преобразования рациональных выражений.
Расширить класс функций, свойства и графики которых известны учащимся; продолжить формирование представлений о таких фундаментальных понятиях математики, какими являются понятия функции, её области определения, ограниченности. Непрерывности, наибольшего и наименьшего значений на заданном промежутке.
Выработать умение выполнять несложные преобразования выражений, содержащих квадратный корень, изучить новую функцию 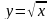 .
.
Навести определённый порядок в представлениях учащихся о действительных (рациональных и иррациональных) числах
Выработать умение выполнять действия над степенями с любыми целыми показателями.
Выработать умения решать квадратные уравнения и уравнения, сводящиеся к кваратным, и применять их при решении задач.
Выработать умения решать линейные и квадратные неравенства с одной переменной; познакомиться со свойствами монотонности функции;
сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
развить логическое мышление и речь — умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
Обучение математике в основной школе направлено на достижение следующих целей:
1. В направлении личностного развития:
• развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;
• формирование у учащихся интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;
• воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;
• формирование качеств мышления, необходимых для адаптации в современном информационном обществе;
• развитие интереса к математическому творчеству и математических способностей.
2. В метапредметном направлении:
• формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;
• развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;
• формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности.
3. В предметном направлении:
• овладение математическими знаниями и умениями, необходимыми для продолжения обучения в старшей школе или иных общеобразовательных учреждениях, изучения смежных дисциплин, применения в повседневной жизни;
• создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности
Место учебного предмета в учебном плане
Согласно Федеральному базисному учебному плану для образовательных учреждений Российской Федерации для обязательного изучения алгебры на этапе основного общего образования отводится не менее 102 часов из расчета 3 часа в неделю.
Личностные, метапредметные и предметные результаты
освоения содержания курса алгебры.
Изучение алгебры по данной программе способствует формированию у учащихся личностных, метапредметных и предметных результатов обучения, соответствующих требованиям федерального государственного образовательного стандарта основного общего образования.
Личностные результаты:
воспитание российской гражданской идентичности: патриотизма, уважения к Отечеству, осознания вклада отечественных учёных в развитие мировой науки;
ответственное отношение к учению, готовность и способность обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию;
осознанный выбор и построение дальнейшей индивидуальной траектории образования на базе ориентировки в мире профессий и профессиональных предпочтений с учётом устойчивых познавательных интересов, а также на основе формирования уважительного отношения к труду, развитие опыта участия в социально значимом труде;
умение контролировать процесс и результат учебной и математической деятельности;
критичность мышления, инициатива, находчивость, активность при решении математических задач.
Метапредметные результаты:
умение самостоятельно определять цели своего обучения, ставить и формулировать для себя новые задачи в учёбе, развивать мотивы и интересы своей познавательной деятельности;
умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией;
умение определять понятия, создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации;
умение устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и делать выводы;
развитие компетентности в области использования информационно-коммуникационных технологий;
первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;
умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
умение находить в различных источниках информацию, необходимую для решения математических задач, и представлять её в понятной форме, принимать решение в условиях неполной или избыточной, точной или вероятностной информации;
умение понимать и использовать математические средства наглядности (графики, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;
умение выдвигать гипотезы при решении задачи, понимать необходимость их проверки;
понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом.
Предметные результаты:
осознание значения математики для повседневной жизни человека;
представление о математической науке как сфере математической деятельности, об этапах её развития, о её значимости для развития цивилизации;
развитие умений работать с учебным математическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли с применением математической терминологии и символики, проводить классификации, логические обоснования;
владение базовым понятийным аппаратом по основным разделам содержания;
систематические знания о функциях и их свойствах;
практически значимые математические умения и навыки, их применение к решению математических и нематематических задач предполагающее умения:
выполнять вычисления с действительными числами;
решать уравнения, неравенства, системы уравнений и неравенств;
решать текстовые задачи арифметическим способом, с помощью составления и решения уравнений, систем уравнений и неравенств;
использовать алгебраический язык для описания предметов окружающего мира и создания соответствующих математических моделей;
проверить практические расчёты: вычисления с процентами, вычисления с числовыми последовательностями, вычисления статистических характеристик, выполнение приближённых вычислений;
выполнять тождественные преобразования рациональных выражений;
выполнять операции над множествами;
исследовать функции и строить их графики;
читать и использовать информацию, представленную в виде таблицы, диаграммы (столбчатой или круговой);
решать простейшие комбинаторные задачи.
II. Планируемые результаты освоения учебного предмета «Математика» (алгебра)
Алгебраические дроби
Выпускник научится:
осуществлять в рациональных выражениях числовые подстановки и выполнять соответствующие вычисления;
выполнять действия сложения и вычитания с алгебраическими дробями;
сокращать дробь;
возводить дробь в степень;
выполнять действия умножения и деления с алгебраическими дробями;
выполнять разложение многочлена на множители применением формул; сокращенного умножения;
выполнять преобразование рациональных выражений;
решать простейшие рациональные уравнения;
понимать уравнение как важнейшую математическую модель для описания и изучения разнообразных реальных ситуаций, решать текстовые задачи алгебраическим методом;
устанавливать, при каких значениях переменной алгебраическая дробь не имеет смысла.
Выпускник получит возможность научиться:
выполнять многошаговые преобразования рациональных выражений, применяя широкий набор способов и приёмов;
выбирать рациональный способ решения;
давать определения алгебраическим понятиям;
работать с заданными алгоритмами;
работать с текстами научного стиля, составлять конспект;
осуществлять сравнение, самостоятельно выбирая основания и критерии для указанных логических операций;
формулировать собственное мнение и позицию, аргументировать и координировать её с позициями партнёров в сотрудничестве при выработке общего решения в совместной деятельности;
работать в группе — устанавливать рабочие отношения, эффективно сотрудничать и способствовать продуктивной кооперации;
Квадратичная функция y = ax2. Функция у = k/х.
Выпускник научится:
находить область определения и область значений функции, читать график функции;
строить графики функций у=ах2, функции у=k/х;
выполнять простейшие преобразования графиков функций;
строить график квадратичной функции,
находить по графику нули функции, промежутки, где функция принимает положительные и отрицательные значения;
решать квадратное уравнение графически;
решать неравенство ах2 +вх+с.≥0 на основе свойств квадратичной функции;
графически решать уравнения и системы уравнений;
графически определять число решений системы уравнений;
понимать функцию как важнейшую математическую модель для описания процессов и явлений окружающего мира, применять функциональный язык для описания и исследования зависимостей между физическими величинами;
упрощать функциональные выражения;
строить графики кусочно-заданных функций;
работать с чертёжными инструментами.
Выпускник получит возможность научиться:
проводить исследования, связанные с изучением свойств функций, в том числе с использованием компьютера; на основе графиков изученных функций строить более сложные графики (кусочно-заданные, с «выколотыми» точками и т. п.);
использовать функциональные представления и свойства функций для решения математических задач из различных разделов курса;
строить графики с использованием возможностей специальных компьютерных инструментов и программ;
задавать вопросы, необходимые для организации собственной деятельности и сотрудничества с партнёром;
осуществлять взаимный контроль и оказывать в сотрудничестве необходимую взаимопомощь;
на основе комбинирования ранее изученных алгоритмов и способов действия решать нетиповые задачи, выполняя продуктивные действия эвристического типа.
Функция у =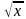 . Свойства квадратного корня.
. Свойства квадратного корня.
Выпускник научится:
извлекать квадратный корень из неотрицательного числа;
строить график функции у =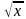 , описывать её свойства;
, описывать её свойства;
применять свойства квадратных корней при нахождении значения выражений;
решать квадратные уравнения, корнями которых являются иррациональные числа;
решать простейшие иррациональные уравнения;
выполнять упрощения выражений, содержащих квадратный корень с применением изученных свойств;
вычислять значения квадратных корней, не используя таблицу квадратов чисел
выполнять преобразования, содержащие операцию извлечения корня;
освобождаться от иррациональности в знаменателе;
раскладывать выражения на множители, способом группировки, используя определение и свойства квадратного корня, формулы квадратов суммы и разности;
оценивать неизвлекаемые корни, находить их приближенные значения;
выполняют преобразования иррациональных выражений: сокращать дроби, раскладывая выражения на множители.
Выпускник получит возможность научиться:
свободно работать с текстами научного стиля;
делать умозаключения (индуктивное и по аналогии) и выводы на основе аргументации, формулировать выводы;
участвовать в диалоге, аргументированно отстаивать свою точку зрения;
понимать точку зрения собеседника, признавать право на иное мнение;
осуществлять проверку выводов, положений, закономерностей, теорем;
осуществлять контроль, коррекцию, оценку действий партнёра, уметь убеждать;
развить представление о числе и числовых системах от натуральных до действительных чисел; о роли вычислений в практике.
Квадратные уравнения
Выпускник научится:
решать неполные квадратные уравнения;
решать квадратные уравнения выделением квадрата двучлена;
решать квадратные уравнения по формуле;
решать задачи с помощью квадратных уравнений;
применять теорему Виета и обратную теорему;
раскладывать на множители квадратный трёхчлен;
решать дробные рациональные уравнения;
решать задачи с помощью рациональных уравнений, выделяя три этапа математического моделирования;
решать рациональные уравнения, используя метод введения новой переменной;
решать биквадратные уравнения;
решать простейшие иррациональные уравнения.
Выпускник получит возможность научиться:
решать квадратные уравнения с параметрами и проводить исследование всех корней квадратного уравнения;
выполнять равносильные переходы при решении иррациональных уравнений разной степени трудности;
воспроизводить теорию с заданной степенью свернутости;
овладеть специальными приёмами решения уравнений и систем уравнений; уверенно применять аппарат уравнений для решения разнообразных задач из математики, смежных предметов, практики;
применять графические представления для исследования уравнений, систем уравнений, содержащих параметр;
составлять план и последовательность действий в связи прогнозируемым результатом;
осуществлять контроль, коррекцию, оценку действий партнера.
Действительные числа
Выпускник научится:
округлять числа, записывать их в стандартном виде;
использовать начальные представления о множестве действительных чисел;
использовать в ходе решения задач элементарные представления, связанные с приближёнными значениями величин;
упрощать выражения, используя определение степени с отрицательным показателем и свойства степени, выполнять преобразования выражений, содержащих степень с отрицательным показателем;
оперировать понятиями «тождество», «тождественное преобразование»; доказывать тождества.
Выпускник получит возможность научиться:
развить представление о числе и числовых системах от натуральных до действительных чисел; о роли вычислений в практике;
развить и углубить знания о десятичной записи действительных чисел (периодические и непериодические дроби);
понять, что числовые данные, которые используются для характеристики объектов окружающего мира, являются преимущественно приближёнными, что по записи приближённых значений, содержащихся в информационных источниках, можно судить о погрешности приближения;
понять, что погрешность результата вычислений должна быть соизмерима с погрешностью исходных данных;
самостоятельно задумывать, планировать и выполнять учебное исследование.
Неравенства
Выпускник научится:
решать неравенства с одной переменной и системы линейных неравенств с одной переменной;
решать квадратные неравенства методом интервалов;
применять свойства числовых неравенств;
исследовать различные функции на монотонность;
понимать и применять терминологию и символику, связанные с отношением неравенства, свойства числовых неравенств;
применять аппарат неравенств для решения задач.
Выпускник получит возможность научиться:
разнообразным приёмам доказательства неравенств; уверенно применять аппарат неравенств для решения разнообразных математических задач и задач из смежных предметов, практики;
применять графические представления для исследования неравенств, систем неравенств, содержащих буквенные коэффициенты (параметры);
использовать различные приёмы поиска информации в Интернете в ходе учебной деятельности;
аргументированно отвечать на поставленные вопросы;
объяснять изученные положения на самостоятельно подобранных конкретных примерах;
организовывать исследование с целью проверки гипотез;
осуществлять коммуникативную рефлексию как осознание оснований собственных действий и действий партнёра.
Элементы логики, комбинаторики, статистики и теории вероятностей
Выпускник научится:
проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждений;
извлекать информацию, представленную в таблицах, на диаграммах, на графиках, составлять таблицы, строить диаграммы и графики;
решать комбинаторные задачи путём систематического перебора возможных вариантов и с использованием правила умножения;
вычислять средние значения результатов измерений;
находить частоту события, используя собственные наблюдения и готовые статистические данные;
находить вероятности случайных событий в простейших случаях.
Выпускник получит возможность научиться:
выстраивать аргументации при доказательстве и в диалоге;
распознавать логически некорректные рассуждения;
записи математических утверждений, доказательств;
анализировать реальные числовые данные, представленных в виде диаграмм, графиков, таблиц;
решению практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин, площадей, объёмов, времени, скорости;
решению учебных и практических задач, требующих систематического перебора вариантов;
сравнению шансов наступления случайных событий, оценки вероятности случайного события в практических ситуациях, сопоставления модели с реальной ситуацией;
пониманию статистических утверждений.
III. Содержание учебного предмета «Математика» (алгебра) 8 класс
Повторение материала 7 класса (2ч.)
Числовые выражения, алгебраические выражения. Линейные уравнения. Системы линейных уравнений. Задачи на составление уравнений. Задачи на составление систем уравнений.
Цель – систематизировать и расширить знания учащихся по изученным темам.
Алгебраические дроби. (22 ч.)
Понятие алгебраической дроби. Основное свойство алгебраической дроби. Сокращение алгебраических дробей. Сложение и вычитание алгебраических дробей. Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень. Рациональное выражение. Рациональное уравнение. Решение рациональных уравнений (первые представления).
Степень с отрицательным целым показателем.
Цель – выработать умение выполнять тождественные преобразования рациональных выражений, научиться выполнять деление многочлена на многочлен, деление многочлена на двучлен по схеме Горнера.
Контрольная работа № 1 по теме «Основное свойство дроби. Сложение и вычитание алгебраических дробей».
Контрольная работа № 2 по теме «Преобразование рациональных выражений. Первые представления о рациональных уравнениях».
Функция 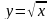 . Свойства квадратного корня. (17 ч.)
. Свойства квадратного корня. (17 ч.)
Рациональные числа. Понятие квадратного корня из неотрицательного числа. Иррациональные числа. Множество действительных чисел. Функция 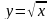 , её свойства и график. Выпуклость функции. Область значений функции. Свойства квадратных корней. Преобразование выражений, содержащих операцию извлечения квадратного корня. Освобождение от иррациональности в знаменателе дроби модуль действительного числа. График функции
, её свойства и график. Выпуклость функции. Область значений функции. Свойства квадратных корней. Преобразование выражений, содержащих операцию извлечения квадратного корня. Освобождение от иррациональности в знаменателе дроби модуль действительного числа. График функции 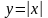 . Формула
. Формула 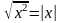 .
.
Цель – систематизировать сведения о рациональных числах и дать представление об иррациональных числах, расширив тем самым понятие числа; выработать умение выполнять простейшие преобразования выражений, содержащих квадратные корни.
Контрольная работа № 3 по теме «Функция 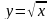 . Свойства квадратного корня».
. Свойства квадратного корня».
Квадратичная функция. Функция 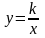 . (17 ч.)
. (17 ч.)
Функция 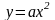 , её график, свойства. Функция
, её график, свойства. Функция 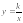 , её свойства, график. Гипербола. Асимптота. Построение графиков функций
, её свойства, график. Гипербола. Асимптота. Построение графиков функций  ,
, 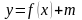 ,
, 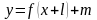 ,
, 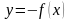 по известному графику функции
по известному графику функции  . Квадратный трёхчлен. Квадратичная функция, её свойства и график. Понятие ограниченной функции. Построение и чтение графиков кусочных функций, составленных из функций
. Квадратный трёхчлен. Квадратичная функция, её свойства и график. Понятие ограниченной функции. Построение и чтение графиков кусочных функций, составленных из функций 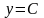 ,
, 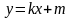 ,
, 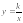 ,
, 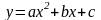 ,
, 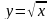 ,
, 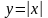 . Графическое решение квадратных уравнений.
. Графическое решение квадратных уравнений.
Цель – выработать умение строить графики квадратичной функции и функции у = k/x.
Контрольная работа №4 по теме «Функции 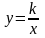 ,
, 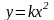 ».
».
Контрольная работа №5 по теме «Функция 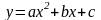 , ее свойства и график».
, ее свойства и график».
Квадратные уравнения. (21 ч.)
Квадратное уравнение. Приведённое (неприведённое) квадратное уравнение. Полное (неполное) квадратное уравнение. Корень квадратного уравнения. Решение квадратного уравнения методом разложения на множители, методом выделения полного квадрата. Дискриминант. Формулы корней квадратного уравнения. Параметр. Уравнение с параметром (начальные представления). Алгоритм решения рационального уравнения. Биквадратное уравнение. Метод введения новой переменной. Рациональные уравнения как математические модели реальных ситуаций. Частные случаи формулы корней квадратного уравнения. Теорема Виета. Разложение квадратного трёхчлена на линейные множители. Иррациональное уравнение. Метод возведения в квадрат.
Цель - выработать умения решать квадратные уравнения, простейшие рациональные уравнения и применять эти знания для решения задач.
Контрольная работа №6 по теме «Формулы корней квадратного уравнения. Рациональные уравнения».
Контрольная работа №7 по теме «Рациональные уравнения как математические модели реальных ситуаций. Иррациональные уравнения».
Неравенства. (16 ч.)
Свойства числовых неравенств. Неравенство с переменной. Решение неравенств с переменной. Линейное неравенство. Равносильные неравенства. Равносильное преобразование неравенства. Квадратное неравенство. Алгоритм решения квадратного неравенства. Возрастающая функция. Убывающая функция. Исследование функций на монотонность (с использованием свойств числовых неравенств). Приближённые значения действительных чисел, погрешность приближения, приближение по недостатку и избытку. Стандартный вид числа.
Цель – выработать умения решать линейные неравенства с одной переменной и их системы, квадратные неравенства, неравенства и уравнения с модулем и параметром.
Контрольная работа №8 по теме «Неравенства».
Обобщающее повторение.
Элементы комбинаторики, статистики и теории вероятностей. (7 ч.)
Простейшие комбинаторные задачи. Организованный перебор вариантов. Дерево вариантов. Комбинаторное правило умножения. ростейшие комбинаторные задачи.
Систематизация и закрепление умений и навыков, полученных на уроках по данным темам
(курс алгебры 8 класс).
Итоговая контрольная работа №9 «Обобщение и систематизация знаний учащихся за курс 8 класса».
IV. Календарно-тематическое планирование по алгебре 8 класс.
| № п/п | Тема учебного занятия | Тип учебного занятия | Дата | |
| план | факт | |||
| Вводное повторение (кол-во часов 2). | ||||
| 1. | Числовые выражения. Линейные уравнения. Системы линейных уравнений. | Урок систематизации ЗУН (урок диалог) | | |
| 2. | Задачи на составление уравнения. Задачи на составление систем уравнений. | Урок систематизации ЗУН (урок диалог) | | |
| Глава 1. Алгебраические дроби (кол-во часов 22). | ||||
| 3. | Основные понятия. | Урок изучения нового материала (урок самостоятельного поиска знаний) | | |
| 4. | Основное свойство алгебраической дроби. | Урок изучения нового материала (урок диалог) | | |
| 5. | Основное свойство алгебраической дроби. | Урок совершенствования ЗУН (урок творчества) | | |
| 6. | Сложение и вычитание дробей с одинаковыми знаменателями. | Урок изучения нового материала (урок самостоятельного поиска знаний) | | |
| 7. | Проверочная работа. Сложение и вычитание дробей с одинаковыми знаменателями. | Урок совершенствования ЗУН (урок практикум) | | |
| 8. | Сложение и вычитание алгебраических дробей с разными знаменателями. | Урок изучения нового материала (урок диалог) | | |
| 9. | Сложение и вычитание алгебраических дробей с разными знаменателями. | Урок совершенствования ЗУН (урок практикум) | | |
| 10. | Сложение и вычитание алгебраических дробей с разными знаменателями. | Урок совершенствования ЗУН (урок практикум) | | |
| 11. | Зачет. Сложение и вычитание алгебраических дробей. | Урок проверки ЗУН | | |
| 12. | Контрольная работа № 1 по теме «Основное свойство дроби. Сложение и вычитание алгебраических дробей». | Урок проверки и оценки ЗУН | | |
| 13. | Умножение и деление алгебраических дробей. | Урок изучения нового материала (урок самостоятельного поиска знаний) | | |
| 14. | Возведение алгебраической дроби в степень. | Урок изучения нового материала (урок диалог) | | |
| 15. | Преобразование рациональных выражений. | Урок изучения нового материала (комбинированный) | | |
| 16. | Преобразование рациональных выражений. | Урок совершенствования ЗУН (урок практикум) | | |
| 17. | Проверочная работа. Преобразование рациональных выражений. | Урок проверки ЗУН | | |
| 18. | Первые представления о рациональных уравнениях. | Урок изучения нового материала (проблемный урок) | | |
| 19. | Первые представления о рациональных уравнениях. | Урок совершенствования ЗУН (урок практикум) | | |
| 20. | Степень с отрицательным целым показателем | Урок изучения нового материала (лекция) | | |
| 21. | Степень с отрицательным целым показателем | Урок совершенствования ЗУН (практикум) | | |
| 22. | Проверочная работа. Степень с отрицательным целым показателем | Урок проверки ЗУН | | |
| 23. | Контрольная работа № 2 по теме «Преобразование рациональных выражений. Первые представления о рациональных уравнениях». | Урок проверки, оценки ЗУН | | |
| 24. | Административная контрольная работа. | | | |
| Глава 2. Функция | ||||
| 25. | Множество рациональных чисел. | Урок изучения нового материала (лекция) | | |
| 26. | Понятие квадратного корня из неотрицательного числа. | Урок изучения нового материала | | |
| 27. | Понятие квадратного корня из неотрицательного числа. | Урок совершенствования ЗУН (практикум) | | |
| 28. | Иррациональные числа. | Урок изучения нового материала (лекция) | | |
| 29. | Множество действительных чисел. | Урок изучения нового материала (лекция) | | |
| 30. | Функция | Урок изучения нового материала (урок диалог) | | |
| 31. | Функция | Урок изучения нового материала (урок диалог) | | |
| 32. | Свойства квадратных корней. | Урок закрепления ЗУН (практикум) | | |
| 33. | Свойства квадратных корней. | Урок закрепления ЗУН (практикум) | | |
| 34. | Преобразование выражений, содержащих операцию извлечения квадратного корня. | Урок изучения нового материала (урок диалог) | | |
| 35. | Преобразование выражений, содержащих операцию извлечения квадратного корня. | Урок совершенствования ЗУН (практикум) | | |
| 36. | Проверочная работа. Преобразование выражений, содержащих операцию извлечения квадратного корня. | Урок проверки ЗУН | | |
| 37. | Преобразование выражений, содержащих операцию извлечения квадратного корня. | Урок обобщения и систематизации знаний | | |
| 38. | Контрольная работа № 3 по теме «Функция | Урок проверки, оценки ЗУН | | |
| 39. | Модуль числа. | Урок изучения нового материала (лекция) | | |
| 40. | Модуль числа. | Урок совершенствования ЗУН (практикум) | | |
| 41. | Проверочная работа. Модуль числа. | Урок совершенствования ЗУН (практикум) | | |
| Глава 3. Квадратичная функция. Функция | ||||
| 42. | Функция | Урок изучения нового материала (комбинированный) | | |
| 43. | Функция | Урок совершенствования ЗУН (практикум) | | |
| 44. | Функция | Урок совершенствования ЗУН (практикум) | | |
| 45. | Функция | Урок изучения нового материала (урок диалог) | | |
| 46. | Функция | Урок совершенствования ЗУН (практикум) | | |
| 47. | Контрольная работа №4 по теме «Функции | Урок проверки, оценки ЗУН. | | |
| 48. | Как построить график функции | Урок изучения нового материала (урок размышления) | | |
| 49. | Как построить график функции | Урок совершенствования ЗУН (урок творчества) | | |
| 50. | Как построить график функции | Урок изучения нового материала (комбинированный) | | |
| 51. | Проверочная работа. Как построить график функции | Урок совершенствования ЗУН (практикум) | | |
| 52. | Как построить график функции | Урок изучения нового материала (урок самостоятельного поиска знаний) | | |
| 53. | Как построить график функции | Урок совершенствования ЗУН (практикум) | | |
| 54. | Функция | Урок изучения нового материала (урок исследования) | | |
| 55. | Функция | Урок усвоения ЗУН (практикум) | | |
| 56. | Функция | Урок усвоения ЗУН (практикум) | | |
| 57. | Графическое решение квадратных уравнений, неравенств | Урок изучения нового материала (урок творчества) | | |
| 58. | Контрольная работа №5 по теме «Функция | Урок проверки, оценки ЗУН | | |
| Глава 4. Квадратные уравнения (кол-во часов 21). | ||||
| 59. | Основные понятия. | Урок изучения нового материала (комбинированный) | | |
| 60. | Основные понятия. | Урок совершенствования ЗУН (практикум) | | |
| 61. | Формулы корней квадратного уравнения. | Урок изучения нового материала (урок исследования) | | |
| 62. | Формулы корней квадратного уравнения. | Урок совершенствования ЗУН | | |
| 63. | Проверочная работа. Формулы корней квадратного уравнения. | Урок проверки ЗУН | | |
| 64. | Рациональные уравнения. | Урок изучения нового материала (комбинированный) | | |
| 65. | Рациональные уравнения. | Урок совершенствования ЗУН (практикум) | | |
| 66. | Проверочная работа. Формулы корней квадратного уравнения. Рациональные уравнения. | Урок проверки ЗУН | | |
| 67. | Контрольная работа №6 по теме «Формулы корней квадратного уравнения. Рациональные уравнения». | Урок проверки, оценки ЗУН | | |
| 68. | Рациональные уравнения как математические модели реальных ситуаций. | Урок изучения нового материала (урок исследования) | | |
| 69. | Рациональные уравнения как математические модели реальных ситуаций. | Урок изучения нового материала (урок исследования) | | |
| 70. | Рациональные уравнения как математические модели реальных ситуаций. | Урок объяснения нового материала | | |
| 71. | Проверочная работа. Рациональные уравнения как математические модели реальных ситуаций. | Урок проверки, оценки ЗУН | | |
| 72. | Еще одна формула корней квадратного уравнения. | Урок изучения нового материала (урок исследования) | | |
| 73. | Еще одна формула корней квадратного уравнения. | Урок совершенствования ЗУН (практикум) | | |
| 74. | Теорема Виета. | Урок изучения нового материала (урок исследования) | | |
| 75. | Проверочная работа. Теорема Виета. | Урок совершенствования ЗУН (практикум) | | |
| 76. | Иррациональные уравнения. | Урок объяснения нового материала (урок лекция) | | |
| 77. | Иррациональные уравнения. | Урок совершенствования ЗУН (практикум) | | |
| 78. | Иррациональные уравнения. | Урок проверки ЗУН (проверочная работа) | | |
| 79. | Контрольная работа №7 по теме «Рациональные уравнения как математические модели реальных ситуаций. Иррациональные уравнения». | Урок проверки, оценки ЗУН | | |
| Глава 5. Неравенства (кол-во часов 16). | ||||
| 80. | Свойства числовых неравенств. | Урок изучения нового материала (лекция) | | |
| 81. | Свойства числовых неравенств. | Урок совершенствования ЗУН (практикум) | | |
| 82. | Свойства числовых неравенств. | Урок совершенствования ЗУН (практикум) | | |
| 83. | Исследование функции на монотонность. | Урок изучения нового материала (лекция) | | |
| 84. | Исследование функции на монотонность. | Урок совершенствования ЗУН (практикум) | | |
| 85. | Решение линейных неравенств. | Урок совершенствования ЗУН | | |
| 86. | Решение линейных неравенств. | Урок совершенствования ЗУН (практикум) | | |
| 87. | Зачет. Решение линейных неравенств. | Урок проверки ЗУН | | |
| 88. | Решение квадратных неравенств. | Урок изучения нового материала (комбинированный) | | |
| 89. | Решение квадратных неравенств. | Урок совершенствования ЗУН (практикум) | | |
| 90. | Решение квадратных неравенств. | Урок обобщения и систематизации знаний | | |
| 91. | Зачет по теме «Неравенства». | Урок проверки, оценки ЗУН | | |
| 92. | Приближенные значения действительных чисел. | Урок изучения нового материала (лекция) | | |
| 93. | Приближенные значения действительных чисел. | Урок совершенствования ЗУН (практикум) | | |
| 94. | Стандартный вид числа. | Урок изучения нового материала (лекция) | | |
| 95. | Контрольная работа №8 по теме «Неравенства». | Урок проверки, оценки ЗУН | | |
| Повторение (кол-во часов 7). | ||||
| 96. | Повторение. Графики функций и их свойства. Простейшие комбинаторные задачи. | Урок обобщения и систематизации ЗУН | | |
| 97. | Повторение. Свойства квадратного корня. Простейшие комбинаторные задачи. Организованный перебор вариантов. | Урок обобщения и систематизации ЗУН | | |
| 98. | Повторение. Алгебраические дроби. Уравнения. Простейшие комбинаторные задачи. Дерево вариантов. | Урок обобщения и систематизации ЗУН | | |
| 99. | Повторение. Решение неравенств. Комбинаторное правило умножения. ростейшие комбинаторные задачи. | Урок совершенствования ЗУН (практикум) | | |
| 100. | Повторение. Решение текстовых задач. Комбинаторное правило умножения. | Урок совершенствования ЗУН (практикум) | | |
| 101. | Итоговая контрольная работа №9 «Обобщение и систематизация знаний учащихся за курс 8 класса». | Урок проверки, оценки ЗУН | | |
| 102. | Анализ результатов контрольной работы. | Урок коррекции. | | |
| | | | | |
V. Контрольно-измерительные материалы учебного предмета «Математика» (алгебра) 8 класс
Перечень контрольных работ.
Контрольная работа № 1 по теме «Основное свойство дроби. Сложение и вычитание алгебраических дробей».
Контрольная работа № 2 по теме «Преобразование рациональных выражений. Первые представления о рациональных уравнениях».
Контрольная работа № 3 по теме «Функция 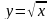 . Свойства квадратного корня».
. Свойства квадратного корня».
Контрольная работа №4 по теме «Функции 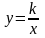 ,
, 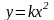 ».
».
Контрольная работа №5 по теме «Функция 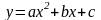 , ее свойства и график».
, ее свойства и график».
Контрольная работа №6 по теме «Формулы корней квадратного уравнения. Рациональные уравнения».
Контрольная работа №7 по теме «Рациональные уравнения как математические модели реальных ситуаций. Иррациональные уравнения».
Контрольная работа №8 по теме «Неравенства».
Итоговая контрольная работа №9 «Обобщение и систематизация знаний учащихся за курс 8 класса».
VI. Ресурсное обеспечение
Настоящая рабочая программа разработана применительно к учебной программе А. Г.
Мордковича «Алгебра» для 7-9 классов и ориентирована на использование учебно -
методического комплекта:
Перечень учебно-методического обеспечения
Программы. Алгебра 7-9 классы. Алгебра и начала математического анализа. 10-11 классы /авт.-сост. И.И. Зубарева, А. Г. Мордкович.-М. : Мнемозина, 2011. -63 с.
Алгебра. 8 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А.Г. Мордкович. – 11-е изд., стер. – М.: Мнемозина, 2014. – 215 с.: ил.
Алгебра. 8 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А.Г. Мордкович и др.]; под ред. А.Г. Мордковича. - 11-е изд., стер. – М.: Мнемозина, 2014. – 255 с.: ил.
Алгебра. 8 класс. Контрольные работы для учащихся общеобразовательных учреждений / Л.А. Александрова; под ред. А.Г. Мордковича. – 2-е изд., испр. – М.: Мнемозина, 2013. – 40
Алгебра. 8 класс. Самостоятельные работы для учащихся общеобразовательных учреждений / Л.А. Александрова; под ред. А.Г. Мордковича. – 5-е изд., стер. – М.: Мнемозина, 2014. – 112 с.: ил.
Алгебра. 8 класс. Блицопрос: пособие для учащихся общеобразовательных учреждений / Е.Е. Тульчинская. – 2-е изд., испр. – М.: Мнемозина, 2013. – 120 с.
Алгебра. 8 класс. Тематические проверочные работы в новой форме для учащихся общеобразовательных учреждений / Л.А. Александрова; под ред. А.Г. Мордковича. – М.: Мнемозина, 2014. – 80 с.: ил.
Тесты по алгебре: 8 класс: к учебнику А.Г. Мордковича «Алгебра. 8 класс» / Е.М. Ключникова, И.В. Комиссарова. – М.: Издательство «Экзамен», 2014. – 94, [2] с. (Серия «Учебно-методический комплект»)
Формирование вычислительных навыков на уроках математики. 5-9 классы / Н.Н. Хлевнюк, М.В. Иванова. – М.: Илекса, 2010. – 248 с.
Дополнительные пособия для учителя.
1. Оценка качества подготовки выпускников основной школы по математике / Г. В. Дорофеев [и др.]. – М. : Дрофа, 2000.
2. Алгебра.8 класс. Подготовка к итоговой аттестации: учебно-тренировочные тесты: в 2 ч. / под ред. Ф. Ф. Лысенко. – Ростов н/Д. : Легион, 2009.
3. Лебединцева, Е. А. Алгебра. 8 класс : задания для обучения и развития учащихся / Е. А. Лебединцева, Е. Ю. Беленкова. – М. : Интеллект-Центр, 2007.
4. Худадатова, С. С. Математика в ребусах, кроссвордах, чайнвордах, криптограммах. 8 класс / С. С. Худадатова. – М. : Школьная Пресса, 2003.
5. Ю.П. Дудницын, Е.Е. Тульчинская. Алгебра. 8 кл. Контрольные работы: Учебное пособие для общеобразовательных учреждений/ Под ред. А.Г. Мордковича.–М.: Мнемозина, 2009. – 48 с.
6. Е. М. Ключникова. Тесты по алгебре: 8 класс: к учебнику А. Г. Мордковича «Алгебра. 8 класс» / Е. М. Ключникова, И. В. Комиссарова. – 2-е изд., стереотип. – М.: Издательство «Экзамен», 2011. – 94 с.
7. М.С. Мильштейн. Алгебра. Рабочая тетрадь (в 2-х частях)/ Под ред. А.Г. Мордковича. – М.: Мнемозина, 2009. – 126 с.
М. А. Попов. Контрольные и самостоятельные работы по алгебре: 8 класс к учебнику А. Г. Мордковича «Алгебра. 8 класс» / М. А. Попов. – 3-е изд. перераб. и доп. – М.: Издательство «Экзамен», 2011 – 63с.
8. Г. Г. Левитас. Карточки для коррекции знаний по математике для 8 – 9 классов. – М.:Илекса, 2009. – 56
9. Контрольно-измерительные материалы. Алгебра: 8 класс / Сост. Л. Ю. Бабушкина. – М.: ВАКО, 2010. – 96 с.
10. А. Н. Рурукин. Поурочные разработки по алгебре: 8 класс. – М.: ВАКО, 2010. – 400 с.
11. И. В. Гришина. Математика (алгебра). 8 класс. Тесты. – Саратов: Лицей, 2011. – Ч. 1 -2. – 64 с.
12. А. П. Иванов. Тематические тесты для систематизации знаний по математике. Ч. 1, 2: Учебн. Пособие. Изд. 3-е, испр. И доп. – М.: Физматкнига, 2009. – 176с.
13. А.Я. Кононов. Задачи по алгебре: Пособие для учащихся 7-9кл. общеобразовательных учреждений.-М.:Просвещение:Учеб.лит.,2009. – 274с.
14. А.П. Ершова, В.В. Голобородько, А.С. Ершова. Самостоятельные и контрольные работы по алгебре и геометрии для 8 класса.-8-е изд., испр. и доп.-М.: ИЛЕКСА, 2010. – 176 с.
15. А. Г. Мерзляк, В. Б. Полонский, Е. М. Рабинович, М. С. Якир. Сборник задач и контрольных работ по алгебре для 8 класса. – Х.: Гимназия, 2010. – 96 с.
16. Л. М. Чернокнижникова. Нестандартные уроки. Математика. 5 – 10 класс: Учебно-методическое пособие – М.: АРКТИ, 2010. – 112 с.
17. В. И. Рыжик. 30 000 уроков математики: Кн. для учителя. – М.: Просвещение, 2009. – 288 с.
Перечень WEB-сайтов для дополнительного образования по предмету:
Министерство образования РФ: http://www.informika.ru/; http://www.ed.gov.ru/
Федеральный портал «Российское образование» : http:/edu.ru/
Российский общеобразовательный портал: http://www.school.edu.ru
Единая коллекция цифровых образовательных ресурсов: http://school-collection.edu.ru
Федеральный институт педагогических измерений: http://www.fipi.ru/
Образовательные ресурсы Интернета - Математика. http://www.alleng.ru/edu/math.htm
Тестирование online: 5 - 11 классы: http://www.kokch.kts.ru/cdo/
Педагогическая мастерская, уроки в Интернет и многое другое: http://teacher.fio.ru/
Новые технологии в образовании: http://edu.secna.ru/main/
Путеводитель «В мире науки» для школьников: http://www.uic.ssu.samara.ru/nauka/
Всё для учёбы: http://www.studfiles.ru












