Работа над определением многогранна.

Работа с определением.

Работа над определением многогранна. Чтобы усвоить определение, нужно установить его, выявить связи между рассматриваемым понятием и близкими к нему, привести примеры, отвечающие определению и не отвечающие ему. Удвоение определения не будет эффективным, если не решать задачи (сначала простые, а потом посложнее) на применение определения. Существует и ряд других сторон этой работы, но начальный этап, как правило, связан с изучением самого текста определения. Многие школьники, а иногда и студенты младших курсов вузов не понимают, что значит принять иное определением. Они считают, что учить определение -- это значит перечитывать его пока не запомнишь («как стихи или прозу»).. Обычно, обнаружив у обучаемых пробелы, аналогичные приведенному выше, приходится так сказать, «спуститься вниз обратившись в работе со старшеклассниками к примерам из начального курса геометрии. Не стоит жалеть для этого времени! Приведем пример. Для начала учащимся предлагается выяснить, справедливо ли «определение»: «Окружностью называется плоская замкнутая линия». Предлагается нарисовать линию, отвечающую этому «Определению». Обычно обучаемые быстро предлагают рисунки (рис1,а, б, в), ясно показывающие непригодность данного определения». Выясняется, что в нем было опущена существенное условие: все точки окружности одинаково удалены от одной и той же точки (центра). Этот пробел и привел к изображению «странных окружностей».

Затем рассматривается второй пример.«Параллелограммом называется четырехугольник, у которого две противоположные стороны параллельны», и снова перед обучаемыми ставится задача привести пример фигуры, соответствующей этому «определению», но не являющейся параллелограммом. Ясно, что такой фигурой манит быть трапеция, ясна и причина возможного несоответствия.

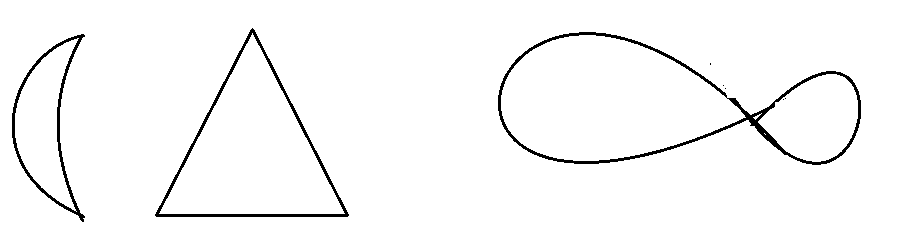
Рис 1 а б в

Введем два понятия.

-Пусть в некотором определении сделано изменение, вызвавшее увеличение объема понятия, тогда полученное «новое» определение не будет равносильно общепринятому. («Новым» оно на- звано иронически, а кавычки только подчеркивают иронию.) В «Логическом словаре» Н. И. Кондакова отмечается, что в этом случае дается слишком широкое определение понятия. Обычно «новое» определение получают, попросту забыв одно из условий. Характеризующие новое понятие.

-Назовем контрпримером к «новому» определению объект (или класс объектов), который отвечает «новому» определению но не отвечает принятому в литературе.

Приведенные выше линии на рисунке 1- это контрпримеры к «новому» определению окружности; трапеция –контрпример к «новому» определению параллелограмма.

Контрпримеры используются еще с древних времен. Рассказывают. что Диоген, услышав определение Платона: «Человек есть двуногое животное без перьев», ощипал петуха, принес его в Академию и заявил: «Вот человек Платона».

Можно порекомендовать учащемуся, начиная самостоятельную работу над определением, не заглядывать в учебник или справочник. Сначала необходимо написать текст определения так, как он себе его представляет, и лишь после этого проверить себя.

Обычно часть определения усваивается сразу еще на уроке. Но в какой-то части определения, возможно, обнаружатся расхождения. ).. В этом случае надо обязательно разобрать- ся, в чем разница, и увидеть, как изменился смысл определяемого понятия. Эта работа помогает понять значение каждого слова в определении и избавляет нас от необходимости «учить» определение: после обдумывания каждого слова в определении оно запоминается само собой.

Бывает, что школьник сразу запомнит определение. Тогда, чтобы понять значение каждого слова (или условия), ему нужно самому посмотреть, что получится, если опустить это слово (условие ).

Рассмотрим примеры. Пусть школьник написал или сказал:

«Два уравнения называются равносильными, если корни одного являются корнями другого». Посмотрел в учебник, а там дополнительно еще два слова: «и обратно. Чтобы осмыслить значение этих слов, надо подобрать два уравнения так, чтобы корни одного были корнями второго, но корни второго не были бы корнями первого, т. е. чтобы не выполнялось второе требование.

Например:

х --2 = 0

х²-4=0

Очевидно. что число 2 является корнем и первого, и второго уравнения, а --2, являясь корнем второго уравнения, корнем первого не является. По «определению» школьника эти уравнения тем не менее равносильны, а на самом деле нет.

Второй пример. Учащийся формулирует «определение»: «Касательной к окружности называется прямая, имеющая с окружностью одну общую точку», а в учебнике написано «только одну».

Школьник привык, что с учебником не поспоришь, Что надо учить так, как в учебнике, но теперь у него возникают сомнения, почему надо именно так. «Разве нельзя,--спрашивает он,-- формулировать по-моему?» Я ему показываю «касательную» АВ (рис 2 ) .

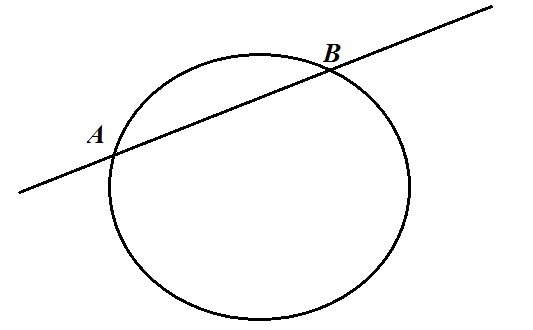
Рис 2.

Он говорит, что это не касательная, а секущая, что она имеет с окружностью две общие точки . Я спрашиваю у него:

-- Но одну общую точку она имеет?

--Имеет.

--Правда, она имеет еще одну. Но в том определении, где сказано «только одну», есть запрет: больше нельзя, а в вашем «определении» иметь две общие точки не запрещается. Следова- тельно, по вашему «определению» прямая АВ тоже будет касательной. Заметим, что благодаря этому «определению» множество касательных к окружности расширилось: к ним добавились прямые (секущие), которые касательными не считаются.

Одна из причин затруднений учащихся состоит в том, что они порой «учат» определения, не уяснив всех терминов, которые в него входят. В частности, читая определение касательной они не задумываются над тем, что значит слово «только». Тщательная работа над текстом определения существенно повышает уровень культуры мышления учащихся, способствует развитию логики мышления и речи обучаемых, повышает интерес к предмету.