Расстояние между точками.

«ЛИПЕЦКИЙ ТЕХНИКУМ СЕРВИСА И ДИЗАЙНА»

Расстояние между точками

Цели занятия:

Образовательные: способствовать

изучению формулы расстояния между

точками в пространстве; закрепить навыки

использования данной формулы при решении

типовых задач.

Развивающие: способствовать развитию

пространственного мышления;

умению сравнивать, обобщать,

запоминать, работать в нужном темпе.

Воспитательные: способствовать

воспитанию личностных качеств

(дисциплинированность, ответственность,

активность, сообразительность)

Задачи занятия:

• Повторить нахождение расстояния

между точками на прямой и на плоскости.

• Получить формулу для нахождения

расстояния между точками в пространстве,

используя метод координат.

• Научиться применять полученную

формулу при решении задач различного

вида.

Ответьте на вопросы:

• Что называется прямоугольной системой координат в пространстве?
• Почему прямоугольную систему координат называют «декартовой» ?
• Как называются координатные прямые Ох, Оу, О z ?
• Что называется координатами точки в пространстве?
• Верны ли утверждения:

1) Точки, лежащие на осях координат, имеют две координаты, равные 0 .

2) Точка, лежащая на координатных плоскостях, имеет одну из координат, равную 0 .

3)Каждой тройке чисел соответствует три точки пространства.

Решите задачи устно:

• Дана точка В(1;-4;2). Найдите абсциссу, ординату и аппликату точки В.
• Что можно сказать о расположении точки, если она имеет координаты:

• (0;1;2)
• (2;0;2)
• (2;1;0)

• Как расположены относительно системы координат точки: А(0;2;0), В(0;0;5), С(0;-1;2), Е(3;0;1), D (3;-3;0), F (1;0;-1).

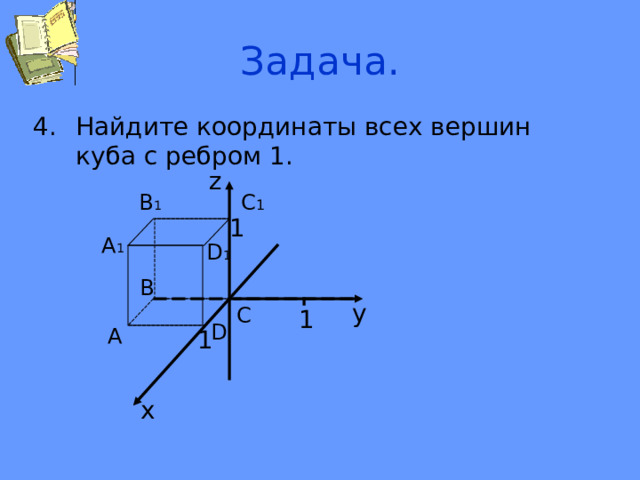
Задача.

• Найдите координаты всех вершин куба с ребром 1.

z

С 1

В 1

1

А 1

D 1

В

у

С

1

D

А

1

х

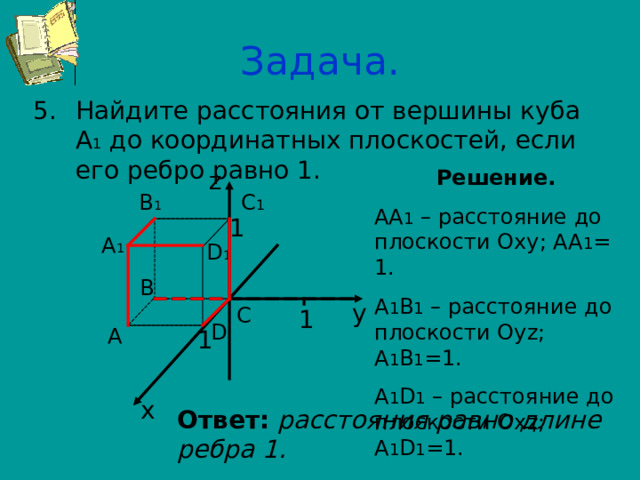
Задача.

• Найдите расстояния от вершины куба А 1 до координатных плоскостей, если его ребро равно 1.

Решение.

АА 1 – расстояние до плоскости Оху; АА 1 = 1.

А 1 В 1 – расстояние до плоскости Оу z ; А 1 В 1 =1.

А 1 D 1 – расстояние до плоскости Ох z ; А 1 D 1 =1.

z

С 1

В 1

1

А 1

D 1

В

у

С

1

D

А

1

х

Ответ: расстояния равно длине ребра 1.

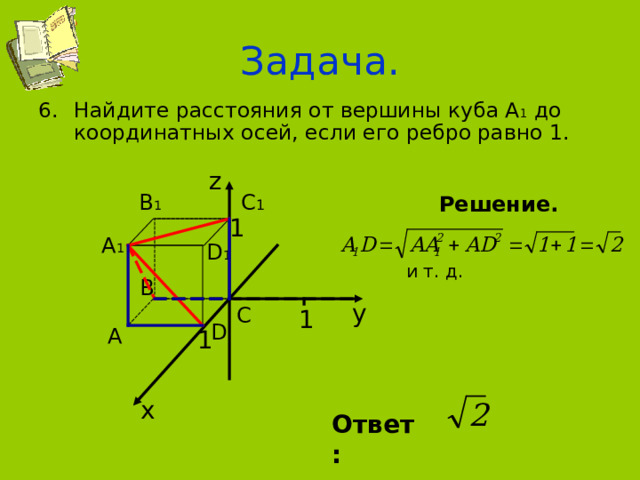
Задача.

• Найдите расстояния от вершины куба А 1 до координатных осей, если его ребро равно 1.

z

В 1

С 1

Решение.

и т. д.

1

А 1

D 1

В

у

С

1

D

А

1

х

Ответ:

Задача. Найдите расстояние от точки А(х; у; z ) до начала координат.

Z

Дано :

A (x; y; z)

О (0; 0; 0)

Найти : ОА

А z (0; 0; z)

A (x; y; z)

A у ( 0 ; y; 0 )

у

O (0; 0; 0)

A х (x; 0 ; 0 )

A 1

х

Решение .

• АА 1 = IzI , т. к. АА 1 =ОА z
• по формуле расстояния между точками на плоскости
• Из ∆ОАА 1 (прямоугольный, ) по т. Пифагора

или

Вывод:

Расстояние от точки А (х; у; z ) пространства до начала координат вычисляется по формуле:

Задача. Найдите расстояние между точками А(х 1 ;у 1 ; z 1 ) и В(х 2 ;у 2 ; z 2 ).

z

Дано :

A (x 1 ; y 1 ; z 1 )

В ( x 2 ; y 2 ; z 2 )

Найти : АВ

F

D

K

А

В

E

N

С

у

Решение.

• АВ – диагональ параллелепипеда BNCEDKAF
• Рёбра параллелепипеда: KA = NC = Iy 2 – y 1 I, CE = NB = Ix 2 - x 1 I, DB = AC = Iz 2 – z 1 I
• АВ ² =ВС ² +АС ² из ∆АВС по т. Пифагора
• BC²=NB²+NC² из ∆ BNC по т. Пифагора
• Тогда АВ ² = NB²+NC² +АС ²

х

Решение.

• Подставим в формулу длины рёбер, тогда

АВ ² =(х 2 – х 1 ) ² +(у 2 - у 1 ) ² +( z 2 - z 1 ) ² .

Следовательно,

Ответ:

Теорема:

Расстояние между точками А 1 (х 1 ; у 1 ; z 1 ) и А 2 (х 2 ; у 2 ; z 2 ) в пространстве выражается формулой:

Задачи на закрепление.

• Найдите расстояние от точки А(1;-2;3) до начала координат.
• Найдите расстояние между точками:

1)А 1 (1;2;-3) и А 2 (-1;1;1);

2)В 1 (3;4;0) и В 2 (3;-1;2).

• Какая из точек А(2;1;5) или В(-2;1;6) лежит ближе к началу координат?
• Найдите координаты точки М, расположенной на оси Ох и равноудалённой от точек А(-2;4;1), В(1;1;2).

Домашнее задание

• Учить конспект.
• Задача . Найдите расстояния от точек А(-2;3;5) и В(1;-4;3)

а) до плоскости Оху;

б) до плоскости Ох z ;

в) до оси Оу;

г) до оси О z ;

д) до начала координат.

• Задача на «4», «5». Даны точки А(-2; 3; 5) и С(3; -1; 2). Найдите точку на оси аппликат, равноудалённую от точек А и С.

в группах

Итоги занятия

Из слова «координата» запишите геометрические понятия или математические слова, которые начинаются на одну из букв. Например, «д» - «диаметр» или «р» - «радиус» .