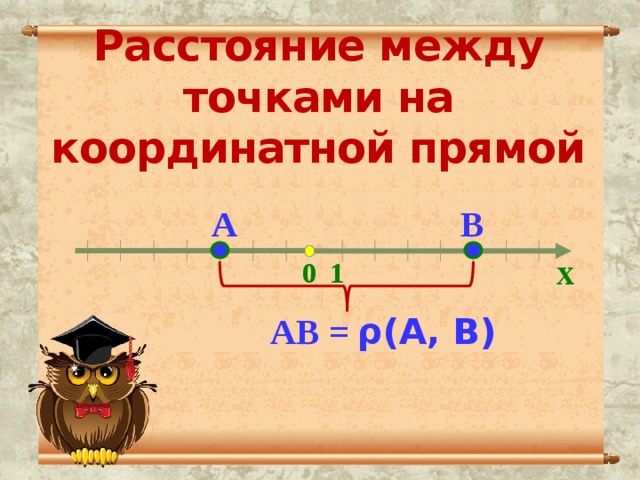
Расстояние между точками на координатной прямой

Расстояние между точками на координатной прямой

А

В

х

1

0

АВ = ρ(А, В)

Расстояние между точками на координатной прямой

Цель урока:

- Найти способ (формулу, правило) для нахождения расстояния между точками на координатной прямой.

- Научиться находить расстояние между точками

на координатной прямой, используя найденное правило.

1. Устный счет

15

+8

-27

-22

+43

-14

-31

2. Устно решите задание с помощью координатной прямой: сколько целых чисел заключено между числами:

а) – 8,9 и 2

б) – 10,4 и – 3,7

в) – 1,2 и 4,6?

а) 10

б) 8

в) 6

• Координатная прямая

положительные числа

отрицательные числа

7

-1

1

0

2

-5

Расстояние от дома до стадиона 6

• Расстояние от дома до школы 6

• Нахождение расстояния между точками на координатной прямой

-5

-1

1

7

2

0

Расстояние между точками будем обозначать буквой ρ (ро)

Расстояние от стадиона до дома 6

• ρ(-5; 1)=6

• Расстояние от школы до дома 6

• ρ(7; 1)=6

• Нахождение расстояния между точками на координатной прямой

7

-1

1

0

2

-5

Расстояние от стадиона до дома 6

• ρ(-5; 1)=6

• Расстояние от школы до дома 6

• ρ(7; 1)=6

ρ(a; b) =

?

|a-b|

Расстояние между точками на координатной прямой

• Расстояние между точками
• a и b равно модулю разности
• координат этих точек.
• ρ(a; b)=|a-b|

Расстояние между двумя точками

x

x

x

b

a

a=b

b

a

Геометрический смысл модуля действительного числа

• Найдите расстояния между точками на координатной прямой

-1

7

1

-5

-6

6

5

4

3

-4

-3

-2

0

2

7

ρ(0; 7)=

ρ(-6; 2)=

8

5

ρ(1; -4) =

ρ(6; 3)=

3

• Найдите расстояния между точками на координатной прямой

-1

7

1

-5

-6

6

5

4

3

-4

-3

-2

0

2

7

ρ(7; 0)=

ρ(2; -6)=

8

5

ρ(-4; 1) =

ρ(3; 6)=

3

Вывод:

значения выражений

| a – b | и | b – a |

равны

при любых значениях а и b

=

Расстояние между точками координатной прямой

+8

– 3

0

11.

|(+8) – (–3)| =

11;

|(–3) – (+8)| =

11;

ρ(–3; 8) =

+17

+4

0

13.

13;

|(+4) – (+17)| =

|(+17) – (+4)| =

ρ(4; 17) =

13;

0

– 16

– 2

14;

ρ(–16; –2) =

14.

|(–16) – (–2)| =

|(–2) – (–16)| =

14;

Найдите ρ(х; у) , если:

1) x = –14, у = –23;

ρ( х ; у )=| х – у |=|–14–(–23)|=|–14+23|=|9|=9

2) x = 5,9, у = –6,8;

ρ( х ; у )=|5,9–(–6,8)|=|5,9+6,8|=|12,7|=12,7

• Продолжить предложение

• 1. Координатная прямая – это прямая
• с указанными на ней …
• 2. Расстояние между двумя точками - это …
• 3. Противоположные числа – это числа, …
• 4. Модулем числа Х называют …

5. - Сравните значения выражений

a – b V b – a сделайте вывод …

- Сравните значения выражений

|a – b| V | b – a| cделайте вывод …

• Винтик и Шпунтик идут по координатному лучу.
• Винтик находится в точке В(236), Шпунтик – в точке Ш(193)
• На каком расстоянии друг от друга находятся Винтик и Шпунтик?

ρ(B, Ш) = 43

Найдите расстояние между точками

• АВ = 1
• АВ = 3
• АВ = 3
• АВ = 11

• А(0), В(1)
• А(2), В(5)
• А(0), В(-3)
• А(-10), В(1 )

Найдите расстояние между точками

• А(-3,5), В(1,4)
• К(1,8), В(4,3)
• А(-10), С(3)

Проверка

АВ =

КВ =

АС =

Найдите координату точки - середины отрезка ВА

С( – 5)

С(–3)

На координатной прямой отмечены точки

А (–3,25) и В (2,65). Найдите координату

точки О – середины отрезка АВ.

Решение:

1) ρ(А;В)= |–3,25 – 2,65| = |–5,9| = 5,9

2) 5,9 : 2 = 2,95

3) –3,25 + 2,95 = –0,3

или 2,65 – 2,95 = –0,3

Ответ: О(–0,3)

На координатной прямой отмечены точки

С( – 5,17) и D(2,33).

Найдите координату точки А – середины

отрезка CD.

Решение:

1) ρ(С; D)= |–5,17 – 2,33| = |–7,5| = 7,5

2) 7,5 : 2 = 3,75

3) –5,17 + 3,75 = –1,42 или 2,33 – 3,75 = –1,42

Ответ: A(–1,42)

Вывод:

Алгоритм нахождения координаты точки – середины данного отрезка:

1. Найти расстояние между точками – концами данного отрезка

• =

2. Разделить результат-1 на 2 (половина величины)

= с

3. Прибавить результат-2 к координате а или

вычесть результат-2 из координаты

а + с или - с

4. Результат-3 есть координата точки - середины данного отрезка

Работа с учебником:

§19, с.112, А. № 573, 575

В. № 578, 580

Домашнее задание:

§19, с.112, А. № 574, 576, В. № 579, 581

подготовиться к КР «Сложение и вычитание рациональных чисел. Расстояние между точками на

координатной прямой»

• Сегодня я узнал…
• Было интересно…
• Я понял, что…
• Теперь я могу…
• Я научился…
• У меня получилось…
• Я попробую…
• Меня удивило…
• Мне захотелось…

До новых встреч!