Просмотр содержимого документа
«Расстояние от точки до прямой»

Расстояние от точки до прямой.
Расстояние между двумя параллельными прямыми

Устная работа
- Какой угол называется внешним углом треугольника?
- Сформулируйте теорему о неравенстве треугольника?
- Как называются стороны в прямоугольном треугольнике?
- Какая сторона является наибольшей в прямоугольном треугольнике? Почему?
- Свойства прямоугольных треугольников
- Признаки равенства прямоугольных треугольников

Устная работа
- Какие прямые называются перпендикулярными?
- Что называют перпендикуляром, проведенным из данной точки к данной прямой?
( это отрезок, лежащий на прямой, перпендикулярной данной, которая проходит через данную точку)
- Сколько перпендикуляров можно провести из точки к данной прямой?
перпендикуляр
наклонная
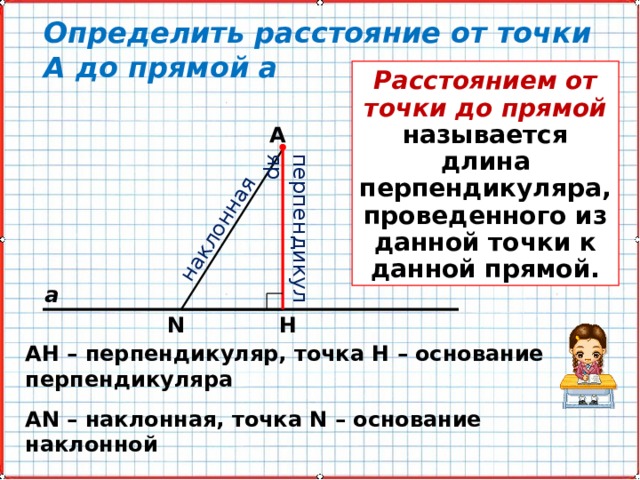
Определить расстояние от точки А до прямой а
Расстоянием от точки до прямой называется длина перпендикуляра, проведенного из данной точки к данной прямой.
А
a
H
N
АН – перпендикуляр, точка Н – основание перпендикуляра
АN – наклонная, точка N – основание наклонной

перпендикуляр
наклонная
А
Сравнить отрезки АH и АN
АH
a
H
N
Перпендикуляр, проведённый из точки к прямой, меньше любой наклонной, проведённой из той же точки к этой прямой.
Устная работа
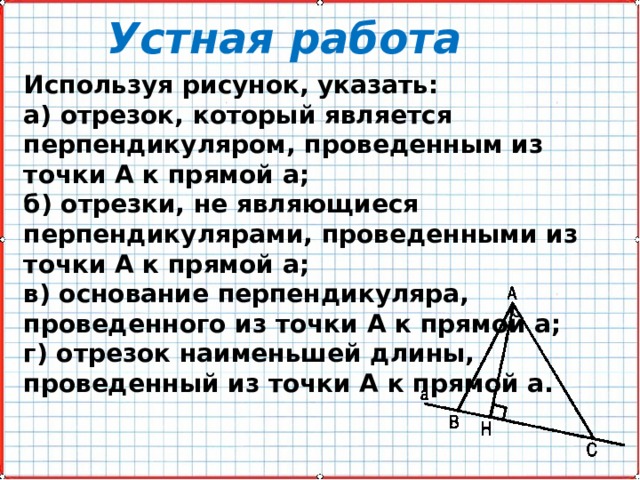
Используя рисунок, указать:
а) отрезок, который является перпендикуляром, проведенным из точки А к прямой а;
б) отрезки, не являющиеся перпендикулярами, проведенными из точки А к прямой а;
в) основание перпендикуляра, проведенного из точки А к прямой а;
г) отрезок наименьшей длины,
проведенный из точки А к прямой а.

Теорема:
Все точки каждой из двух параллельных прямых равноудалены от другой прямой.
~
Если a || b, AB b, MN b, то AB = MN.
Доказательство:
M
A
a
Доп. построение: АN
Если MN b , то MN a.
Δ ABN = Δ NMA (по гипотенузе и острому углу)
b
N
B
Следовательно, AB = MN .
Теорема доказана.
7
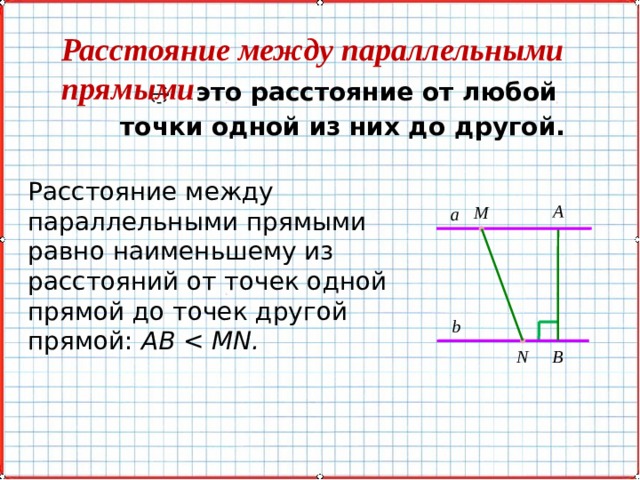
Расстояние между параллельными прямыми
̶ это расстояние от любой
точки одной из них до другой.
Расстояние между параллельными прямыми равно наименьшему из расстояний от точек одной прямой до точек другой прямой: AB MN.
A
M
a
b
B
N
8
Решение задач
оформить в тетрадь
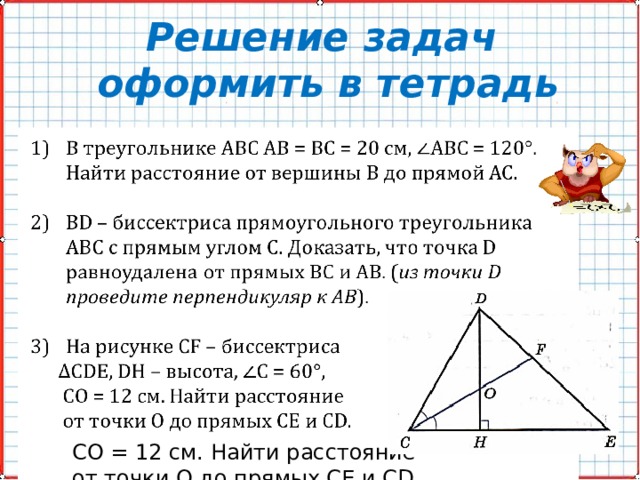
- В треугольнике АВС АВ = ВС = 20 см, АВС = 120°. Найти расстояние от вершины В до прямой АС.
- ВD – биссектриса прямоугольного треугольника АВС с прямым углом С. Доказать, что точка D равноудалена от прямых ВС и АВ. ( из точки D проведите перпендикуляр к AB ).
- На рисунке СF – биссектриса
∆ СDЕ, DH – высота, С = 60°,
СО = 12 см. Найти расстояние
от точки О до прямых СЕ и СD.

Задание:
- Изучить материал п.39 на стр. 81 – 83, выучить правила
- Решить № 271, 272.


























