Расстояние между точками

Декартовы координаты

Расстояние между точками.

=

=

Отметьте точки

A (1; 5) и B (7; 9) . Отметьте середину M отрезка AB .

Запишите координаты точки

Запишите формулы для расчета координат середины отрезка.

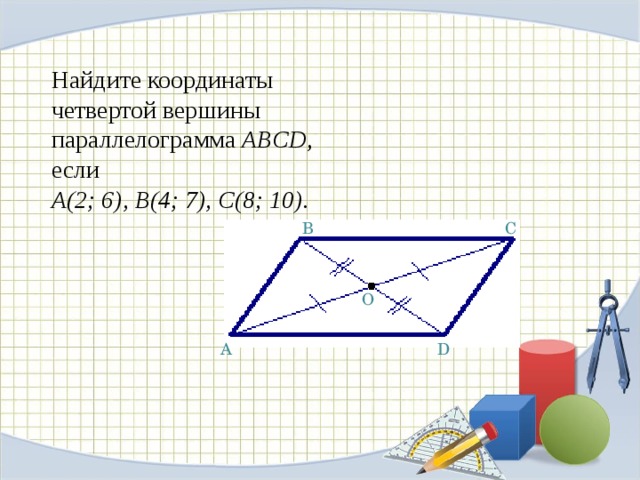
Найдите координаты четвертой вершины параллелограмма ABCD , если А(2; 6), В(4; 7), С(8; 10).

В

С

О

D

А

Координаты середины О диагонали АС :

Координаты середины О диагонали BD :

Значит координаты точки

В

С

О

А

D

D

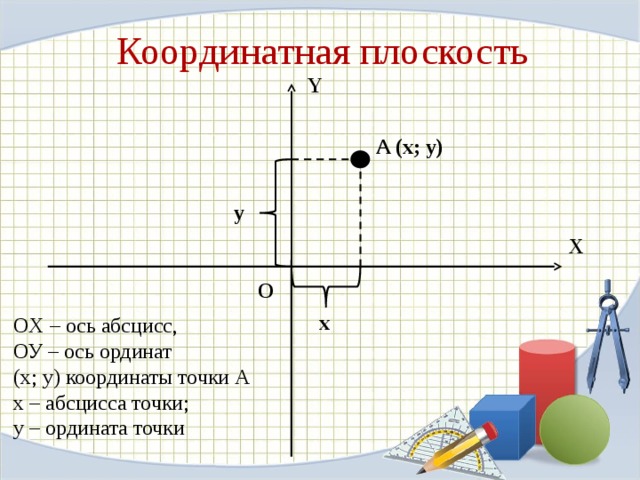
Координатная плоскость

Y

A (x; y)

y

X

O

x

OX – ось абсцисс,

ОУ – ось ординат

(х; у) координаты точки А

х – абсцисса точки;

у – ордината точки

Рене Декарт

французский философ, математик, механик, физик и физиолог, создатель аналитической геометрии и современной алгебраической символики, автор метода радикального сомнения в философии, механицизма в физике.

Координаты середины отрезка

А

Пусть имеются точки:

А(, точка С (х; у) середина отрезка АВ, тогда

С

у

В

х

Длина отрезка (расстояние между точками)

А

Пусть имеются точки:

А(, тогда

d – расстояние между точками А и В

d=

В

Найти расстояние между точками А и В, если:

• А(7;4), В(3;1)
• А(3;5), В(1;1)
• А(4;-1), В(-2;5)

АВ=5

№ 19. Найти на оси ох точку, равноудаленную от точек (1;2) и (2;3)

• Пусть искомая точка Х(х;у). Так как точка лежит на оси ох, то у=0, значит Х(х;0).
• А(1;2)и В(2;3). АХ=ВХ.

Итоги урока

• Достигли ли мы поставленной цели?
• Какой главный итог нашего урока?
• Что мы использовали для достижения цели урока?

д/з

К.в1-5

№ 17,16