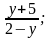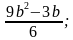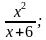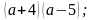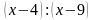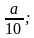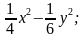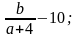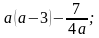Рациональные выражения.
Прежде, чем ввести понятие рационального выражения, определим понятия целого и дробного выражения.
Целым называется выражение, которое состоит из чисел, переменных и знаков арифметических действий (сложение, вычитание, возведение в степень), включая деление на какое-либо число, отличное от нуля.
Например, 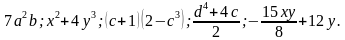
Поскольку в целом выражении может производиться деление на число, не равное нулю, то целое выражение имеет смысл всегда!
Дробным называется выражение, которое состоит из чисел, переменных, знаков арифметических действий (сложение, вычитание, возведение в степень), включая деление на выражение с переменной.
Например, 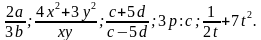
Поскольку в дробном выражении производится деление на выражение с переменной, то дробное выражение имеет смысл не всегда! Ведь возможны такие значения переменных, при которых знаменатель равен нулю! Так вот…
Значения переменных, входящих в дробное выражение, при которых это выражение имеет смысл, называются допустимыми значениями переменных.
Например:
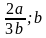 – любое число, кроме
– любое число, кроме 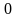 , т.к.
, т.к. 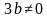
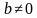
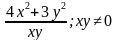
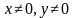 (т.е. x и y – любые, кроме нуля)
(т.е. x и y – любые, кроме нуля)
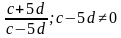
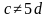 (т.е. c и d могут быть любыми, кроме тех случаев, когда
(т.е. c и d могут быть любыми, кроме тех случаев, когда
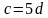 или
или 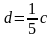 )
)
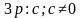
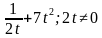
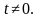
Целые и дробные выражения – это два больших множества математических выражений. Если их объединить, то получим множество рациональных выражений.
Рациональным выражением называется множество всех целых и дробных выражений.
Одним из частных случаев рациональных выражений является дробь, числитель и знаменатель которой – многочлены. Такая дробь называется рациональной.
Рациональной дробью называется дробь, числитель и знаменатель которой представлены в виде многочлена.
Например, 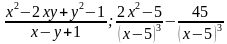 .
.
Также, как и в дробном выражении, допустимыми значениями переменных называются те их значения, которые не обращают в нуль знаменатель рациональной дроби.
Определите, какие из приведённых выражений являются целыми, а какие – дробными. В каждом из этих выражений укажите допустимые значения переменных.
Из рациональных выражений:
выпишите те, которые являются:
целыми выражениями;
дробными выражениями.
Найдите значение выражения:
Заполните таблицы:
Найдите, при каких значениях переменной не имеет смысла рациональная дробь:
Найдите, при каких значениях переменной имеет смысл рациональная дробь:
Составьте дробь, у которой:
числитель является суммой переменных  и
и  , а знаменатель – разностью этих переменных;
, а знаменатель – разностью этих переменных;
числитель является произведением переменных  и
и  , а знаменатель – суммой их квадратов;
, а знаменатель – суммой их квадратов;
числитель является удвоенной разностью переменных  и
и  , а знаменатель – квадратом суммы этих переменных;
, а знаменатель – квадратом суммы этих переменных;
числитель является разностью квадратов переменных  и
и  , а знаменатель – произведением их кубов.
, а знаменатель – произведением их кубов.
Велосипедист проехал по шоссе  км со скоростью
км со скоростью  км/ч, по просёлочной дороге
км/ч, по просёлочной дороге  км со скоростью, на
км со скоростью, на  км/ч меньшей, чем по шоссе. Сколько времени затратил велосипедист на всю дорогу? Составьте выражение и найдите его значение при
км/ч меньшей, чем по шоссе. Сколько времени затратил велосипедист на всю дорогу? Составьте выражение и найдите его значение при  и
и  .
.
Расстояние от  до
до  автобус проехал со скоростью
автобус проехал со скоростью  км/ч, а расстояние от
км/ч, а расстояние от  до
до  – со скоростью
– со скоростью  км/ч. Сколько времени затратил автобус на весь путь, если
км/ч. Сколько времени затратил автобус на весь путь, если  км,
км,  км? Составьте выражение и найдите его значение при
км? Составьте выражение и найдите его значение при 
Укажите допустимые значения переменной в выражении:
При каком значении  значение дроби
значение дроби  :
:
равно 0; | равно 1; | больше 1; | меньше 1? |
При каком значении  значение дроби
значение дроби  :
:
равно 0; | равно 1; | больше 1; | меньше 1? |
Найдите допустимые значения переменной в выражении:
Составьте дробь с переменной  , которая имеет смысл при всех значениях
, которая имеет смысл при всех значениях  , кроме:
, кроме:
Составьте дробь с переменной  , которая имеет смысл при всех значениях
, которая имеет смысл при всех значениях  , кроме:
, кроме:
2







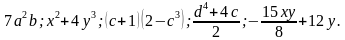
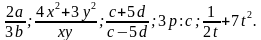
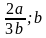 – любое число, кроме
– любое число, кроме 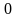 , т.к.
, т.к. 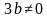
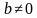
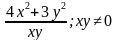
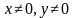 (т.е. x и y – любые, кроме нуля)
(т.е. x и y – любые, кроме нуля)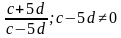
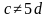 (т.е. c и d могут быть любыми, кроме тех случаев, когда
(т.е. c и d могут быть любыми, кроме тех случаев, когда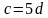 или
или 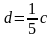 )
)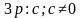
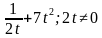
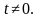
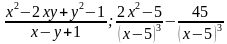 .
.