класс (решения)
Задача 10.1. Всю поверхность куба 13 × 13 × 13 покрасили в красный цвет, а затем этот куб распилили на кубики 1 × 1 × 1. Все грани кубиков 1 × 1 × 1, не окрашенные в красный цвет, покрасили в синий цвет. Во сколько раз суммарная площадь синих граней больше суммарной площади красных граней?
Ответ: 12.
Решение. Каждая грань исходного куба состоит ровно из 132 квадратиков 1 × 1, поэтому всего в красный цвет оказались окрашены 6 ⋅ 132 квадратиков 1 × 1. Поскольку всего куби- ков 1 × 1 × 1 ровно 133, и у каждого из них 6 граней, то в синий цвет оказались окрашены 6 ⋅ 133 − 6 ⋅ 132 квадратиков 1 × 1. Значит, ответом в задаче является число
6 ⋅ 133 − 6 ⋅ 132
6 ⋅ 132 = 13 − 1 = 12.
 Замечание. Тот же ответ можно было получить и по-другому, поняв, что каждому красно- му квадратику 1 × 1 на поверхности исходного куба соответствует ровно 12 синих квадра- тиков 1 × 1 внутри этого куба. Эти 12 синих квадратиков получаются из красного после- довательным применением параллельного переноса на вектор длины 1 «вглубь куба», перпендикулярный грани красного квадратика.
Замечание. Тот же ответ можно было получить и по-другому, поняв, что каждому красно- му квадратику 1 × 1 на поверхности исходного куба соответствует ровно 12 синих квадра- тиков 1 × 1 внутри этого куба. Эти 12 синих квадратиков получаются из красного после- довательным применением параллельного переноса на вектор длины 1 «вглубь куба», перпендикулярный грани красного квадратика.
Задача 10.2. Дано натуральное число 𝑛. Рома выписал на доску три числа 𝑛, 𝑛 + 1, 𝑛 + 2 друг за другом, без пробелов. У него получилась некоторая последовательность цифр, в которой есть подряд идущие цифры 6474. Найдите наименьшее возможное значение 𝑛.
Ответ: 46.
Решение. Ясно, что для 𝑛 = 46 условие выполняется.

Предположим, существует 𝑛 . В одном из трёх чисел Ромы должна быть цифра 6, и при 𝑛 она должна быть в разряде единиц. Несложным перебором можно убедиться, что соответствующие значения 𝑛 = 4, 5, 6, 14, 15, 16, 24, 25, 26, 34, 35, 36, 44, 45 не подходят.
Задача 10.3. На стороне 𝐴𝐷 прямоугольника 𝐴𝐵𝐶𝐷 отмечена точка 𝐸. На отрезке 𝐸𝐶 на- шлась такая точка 𝑀, что 𝐴𝐵 = 𝐵𝑀, 𝐴𝐸 = 𝐸𝑀. Найдите длину стороны 𝐵𝐶, если известно, что 𝐸𝐷 = 16, 𝐶𝐷 = 12.
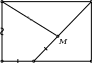
𝐵 𝐶
12
𝐴 𝐸 16 𝐷
Ответ: 20.
Решение. Заметим, что треугольники 𝐴𝐵𝐸 и 𝑀𝐵𝐸 равны друг другу по трём сторонам. Тогда ∠𝐵𝑀𝐸 = ∠𝐵𝐴𝐸 = 90∘.
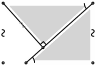
𝐵 𝐶
𝐴 𝐸 𝐷
Рис. 6: к решению задачи 10.3
 Из параллельности 𝐴𝐷 и 𝐵𝐶 следует ∠𝐵𝐶𝑀 = ∠𝐶𝐸𝐷 (рис. 6). Значит, прямоугольные треугольники 𝐵𝐶𝑀 и 𝐶𝐸𝐷 равны по острому углу и катету 𝐵𝑀 = 𝐴𝐵 = 𝐶𝐷. Используя теорему Пифагора для треугольника 𝐶𝐷𝐸, заключаем
Из параллельности 𝐴𝐷 и 𝐵𝐶 следует ∠𝐵𝐶𝑀 = ∠𝐶𝐸𝐷 (рис. 6). Значит, прямоугольные треугольники 𝐵𝐶𝑀 и 𝐶𝐸𝐷 равны по острому углу и катету 𝐵𝑀 = 𝐴𝐵 = 𝐶𝐷. Используя теорему Пифагора для треугольника 𝐶𝐷𝐸, заключаем
𝐵𝐶 = 𝐶𝐸 = √𝐶𝐷2 + 𝐸𝐷2 = √122 + 162 = 20.
Задача 10.4. Дан квадратный трёхчлен 𝑃(𝑥). Известно, что уравнения 𝑃(𝑥) = 𝑥 − 2 и
𝑃(𝑥) = 1 − 𝑥/2 имеют ровно по одному корню. Чему равен дискриминант 𝑃(𝑥)?
Ответ: −1/2.
Решение. Пусть 𝑃(𝑥) = 𝑎𝑥2 + 𝑏𝑥 + 𝑐, 𝑎 ≠ 0. Рассмотрим первое квадратное уравнение и его дискриминант:
𝑎𝑥2 + 𝑏𝑥 + 𝑐 = 𝑥 − 2;
𝑎𝑥2 + 𝑥(𝑏 − 1) + (𝑐 + 2) = 0;
𝐷1 = (𝑏 − 1)2 − 4𝑎(𝑐 + 2).
Рассмотрим теперь второе квадратное уравнение и его дискриминант:
𝑎𝑥2 + 𝑏𝑥 + 𝑐 = 1 − 𝑥/2;
𝑎𝑥2 + 𝑥(𝑏 + 1/2) + (𝑐 − 1) = 0;
𝐷2 = (𝑏 + 1/2)2 − 4𝑎(𝑐 − 1).
Поскольку квадратные уравнения имеют по одному корню, оба этих дискриминанта рав- ны нулю. Получаем систему
(𝑏 − 1)2 − 4𝑎(𝑐 + 2) = 0,
{
(𝑏 + 1/2)2 − 4𝑎(𝑐 − 1) = 0.
Раскрыв скобки, получим
𝑏2 − 2𝑏 + 1 − 4𝑎𝑐 − 8𝑎 = 0,
{
𝑏2 + 𝑏 + 1/4 − 4𝑎𝑐 + 4𝑎 = 0.
Сложив первое уравнение и удвоенное второе, получим
𝑏2 − 2𝑏 + 1 − 4𝑎𝑐 − 8𝑎 + 2 ⋅ (𝑏2 + 𝑏 + 1/4 − 4𝑎𝑐 + 4𝑎) = 0;
3𝑏2 − 12𝑎𝑐 + 3/2 = 0;
𝑏2 − 4𝑎𝑐 = −1/2.
 А это и есть дискриминант 𝑃(𝑥).
А это и есть дискриминант 𝑃(𝑥).
Задача 10.5. У жадины Вовочки 25 одноклассников. В честь своего Дня Рождения он при- нёс в класс 200 конфет. Мама Вовочки, чтобы он не съел всё сам, велела раздать конфеты так, чтобы у любых 16 его одноклассников суммарно оказалось хотя бы 100 конфет. Какое наибольшее количество конфет Вовочка может оставить себе, выполнив при этом прось- бу мамы?
Ответ: 37.
Решение. Среди всех 25 одноклассников выберем 16 людей с наименьшим числом вы- данных конфет. Заметим, что среди них есть человек, которому выдали не меньше 7 кон- фет (иначе, если им всем выдали не больше 6 конфет, то суммарно им выдали не больше 16 ⋅ 6 = 96 конфет, что меньше 100). Тогда и оставшимся 25 − 16 = 9 одноклассникам вы- дали не меньше 7 конфет. Тогда всего конфет суммарно выдали хотя бы 100 + 9 ⋅ 7 = 163. Соответственно, Вовочка оставил себе не более 200 − 163 = 37 конфет.
Заметим также, что Вовочка мог себе оставить ровно 37 конфет, если остальные 163 он выдал одноклассникам так: 13 одноклассникам выдал по 7 конфет, а 12 одноклассникам выдал по 6 конфет. Тогда у любых 16 человек суммарно хотя бы 6 ⋅ 12 + 7 ⋅ 4 = 100 конфет,
 а всего Вовочка действительно выдал 13 ⋅ 7 + 12 ⋅ 6 = 163 конфеты.
а всего Вовочка действительно выдал 13 ⋅ 7 + 12 ⋅ 6 = 163 конфеты.
Задача 10.6. В выпуклом четырёхугольнике 𝐴𝐵𝐶𝐷 отмечена середина стороны 𝐴𝐷 — точка 𝑀. Отрезки 𝐵𝑀 и 𝐴𝐶 пересекаются в точке 𝑂. Известно, что ∠𝐴𝐵𝑀 = 55∘, ∠𝐴𝑀𝐵 = 70∘, ∠𝐵𝑂𝐶 = 80∘, ∠𝐴𝐷𝐶 = 60∘. Сколько градусов составляет угол 𝐵𝐶𝐴?
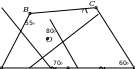
𝐴
𝑀 𝐷
Ответ: 35.
Решение. Поскольку
∠𝐵𝐴𝑀 = 180∘ − ∠𝐴𝐵𝑀 − ∠𝐴𝑀𝐵 = 180∘ − 55∘ − 70∘ = 55∘ = ∠𝐴𝐵𝑀,
треугольник 𝐴𝐵𝑀 является равнобедренным, и 𝐴𝑀 = 𝐵𝑀.
Заметим, что ∠𝑂𝐴𝑀 = 180∘ − ∠𝐴𝑂𝑀 − ∠𝐴𝑀𝑂 = 180∘ − 80∘ − 70∘ = 30∘, поэтому ∠𝐴𝐶𝐷 = 180∘ − ∠𝐶𝐴𝐷 − ∠𝐴𝐷𝐶 = 180∘ − 30∘ − 60∘ = 90∘.
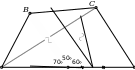
𝐴
𝑀 𝐷
Рис. 7: к решению задачи 10.6
Проведём отрезок 𝐶𝑀 (рис 7). Поскольку в прямоугольном треугольнике медиана, про- ведённая к гипотенузе, равна её половине, имеем 𝐶𝑀 = 𝐷𝑀 = 𝐴𝑀 = 𝐵𝑀. Треугольник
𝑀𝐶𝐷 является равнобедренным с углом 60∘ при основании, поэтому он является равно- сторонним, и ∠𝐶𝑀𝐷 = 60∘. Тогда ∠𝐵𝑀𝐶 = 180∘ − ∠𝐴𝑀𝐵 − ∠𝐶𝑀𝐷 = 180∘ − 70∘ − 60∘ = 50∘. Поскольку треугольник 𝐵𝑀𝐶 является равнобедренным с вершиной 𝑀, имеем ∠𝐶𝐵𝑀 =
1 (180∘ − ∠𝐵𝑀𝐶) = 1 (180∘ − 50∘) = 65∘. Наконец,
2 2
 ∠𝐵𝐶𝐴 = 180∘ − ∠𝐶𝐵𝑀 − ∠𝐵𝑂𝐶 = 180∘ − 65∘ − 80∘ = 35∘.
∠𝐵𝐶𝐴 = 180∘ − ∠𝐶𝐵𝑀 − ∠𝐵𝑂𝐶 = 180∘ − 65∘ − 80∘ = 35∘.
Замечание. Существуют и другие решения, использующие тот факт, что 𝐴𝐵𝐶𝐷 является вписанным четырёхугольником с центром описанной окружности 𝑀.
Задача 10.7. Квадратную доску 30 × 30 разрезали по линиям сетки на 225 частей одина- ковой площади. Найдите наибольшее возможное значение суммарной длины разрезов.
Ответ: 1065.
Решение. Общая длина разрезов равна сумме периметров всех фигур, уменьшенной на периметр квадрата, поделённой на 2 (каждый разрез примыкает ровно к двум фигурам). Значит, чтобы получить максимальную длину разрезов, периметры фигур должны быть максимально возможными.
225
Площадь каждой фигурки равна
900 = 4. А четырёхклеточных фигур всего 5:




У квадрата периметр равен 8, а у всех других фигурок — 10. Получаем, что максимальная длина разрезов не превосходит (225 ⋅ 10 − 120)/2 = 1065.

 Осталось привести пример. Из доказанного выше следует, что данный ответ получится, если мы разрежем квадрат 30 × 30 на любые четырёхклеточные фигурки, кроме квадрата. Заполним сначала прямоугольник 28×30 полосками 1×4, останется прямоугольник 2×30. Прямоугольник 2 ×24 также разрежем на полоски 1 ×4. Останется пустой прямоугольник 2 × 6, который легко можно разрезать на две фигурки в виде буквы Г и одну полоску 1 × 4, как показано на рис 8.
Осталось привести пример. Из доказанного выше следует, что данный ответ получится, если мы разрежем квадрат 30 × 30 на любые четырёхклеточные фигурки, кроме квадрата. Заполним сначала прямоугольник 28×30 полосками 1×4, останется прямоугольник 2×30. Прямоугольник 2 ×24 также разрежем на полоски 1 ×4. Останется пустой прямоугольник 2 × 6, который легко можно разрезать на две фигурки в виде буквы Г и одну полоску 1 × 4, как показано на рис 8.












 Рис. 8: к решению задачи 10.7
Рис. 8: к решению задачи 10.7
Задача 10.8. Натуральное число 1 ⩽ 𝑛 ⩽ 221 назовём удачным, если при делении 221
на 𝑛 остаток нацело делится на неполное частное (при этом остаток может быть равен 0). Сколько всего удачных чисел?
Ответ: 115.
Решение. Пусть для некоторого удачного числа 𝑛 неполное частное равно 𝑘, а остаток равен 𝑘𝑠, по определению он неотрицателен и меньше делителя 𝑛 (из условия следует, что 𝑘 — натуральное число, а 𝑠 — целое неотрицательное.) Тогда
221 = 𝑛𝑘 + 𝑘𝑠 = 𝑘(𝑛 + 𝑠).
Поскольку 221 = 13 ⋅ 17 делится на натуральное число 𝑘, получаем несколько случаев.
2
Пусть 𝑘 = 1, тогда 𝑛 + 𝑠 = 221. Поскольку 0 ⩽ 𝑠 , то 221 ⩾ 𝑛 ⩾ 𝑛+𝑠 = 110, 5 110. Заметим, что все такие 𝑛 ∈ {111, 112, 113, … , 221} являются удачными (и таких чисел ровно 111). Действительно, во всех этих случаях 221 = 𝑛⋅1+(221−𝑛) остаток (221−𝑛) неотрицателен, меньше соответствующего 𝑛, а также делится на соответствующее неполное частное 1. Пусть 𝑘 = 13, тогда 𝑛 + 𝑠 = 17. Поскольку 0 ⩽ 13𝑠 𝑛, то 17 = 𝑛 + 𝑠 14𝑠, т.е. либо
𝑠 = 0 и 𝑛 = 17, либо 𝑠 = 1 и 𝑛 = 16. Заметим, что числа 𝑛 = 16 и 𝑛 = 17 являются удачными. Действительно, в обоих случаях 221 = 16⋅13+13 и 221 = 17⋅13+0 остаток неотрицателен, меньше соответствующего 𝑛, а также делится на соответствующее неполное частное.
Пусть 𝑘 = 17, тогда 𝑛 + 𝑠 = 13. Поскольку 0 ⩽ 17𝑠 , то 13 = 𝑛 + 𝑠 18𝑠, т.е. 𝑠 = 0 и 𝑛 = 13. Заметим, что 𝑛 = 13 является удачным. Действительно, в случае 221 = 13 ⋅ 17 + 0 остаток неотрицателен, меньше соответствующего 𝑛, а также делится на соответствующее неполное частное.
Пусть 𝑘 = 221, тогда 𝑛 + 𝑠 = 1. Поскольку 0 ⩽ 221𝑠 𝑛, то 1 = 𝑛 + 𝑠 222𝑠, т.е.
𝑠 = 0 и 𝑛 = 1. Заметим, что 𝑛 = 1 является удачным. Действительно, в случае 221 = 1 ⋅ 221 + 0 остаток неотрицателен, меньше соответствующего 𝑛, а также делится на соответствующее неполное частное.
 Итого всего удачных чисел 111 + 2 + 1 + 1 = 115.
Итого всего удачных чисел 111 + 2 + 1 + 1 = 115.







 Замечание. Тот же ответ можно было получить и по-другому, поняв, что каждому красно- му квадратику 1 × 1 на поверхности исходного куба соответствует ровно 12 синих квадра- тиков 1 × 1 внутри этого куба. Эти 12 синих квадратиков получаются из красного после- довательным применением параллельного переноса на вектор длины 1 «вглубь куба», перпендикулярный грани красного квадратика.
Замечание. Тот же ответ можно было получить и по-другому, поняв, что каждому красно- му квадратику 1 × 1 на поверхности исходного куба соответствует ровно 12 синих квадра- тиков 1 × 1 внутри этого куба. Эти 12 синих квадратиков получаются из красного после- довательным применением параллельного переноса на вектор длины 1 «вглубь куба», перпендикулярный грани красного квадратика. 𝐵 𝐶
𝐵 𝐶  𝐵 𝐶
𝐵 𝐶 
 𝐴 𝑀 𝐷
𝐴 𝑀 𝐷 



 Осталось привести пример. Из доказанного выше следует, что данный ответ получится, если мы разрежем квадрат 30 × 30 на любые четырёхклеточные фигурки, кроме квадрата. Заполним сначала прямоугольник 28×30 полосками 1×4, останется прямоугольник 2×30. Прямоугольник 2 ×24 также разрежем на полоски 1 ×4. Останется пустой прямоугольник 2 × 6, который легко можно разрезать на две фигурки в виде буквы Г и одну полоску 1 × 4, как показано на рис 8.
Осталось привести пример. Из доказанного выше следует, что данный ответ получится, если мы разрежем квадрат 30 × 30 на любые четырёхклеточные фигурки, кроме квадрата. Заполним сначала прямоугольник 28×30 полосками 1×4, останется прямоугольник 2×30. Прямоугольник 2 ×24 также разрежем на полоски 1 ×4. Останется пустой прямоугольник 2 × 6, который легко можно разрезать на две фигурки в виде буквы Г и одну полоску 1 × 4, как показано на рис 8.


 Рис. 8: к решению задачи 10.7
Рис. 8: к решению задачи 10.7









