класс (решения)
Задача 8.1. Перед пессимистом и оптимистом стоит по стакану (стаканы одинаковы). Каждому из них в стакан налили воды так, что стакан пессимиста оказался на 60% пуст, а стакан оптимиста, наоборот, на 60% полон. Оказалось, что воды в стакане пессимиста на 46 миллилитров меньше, чем в стакане оптимиста. Сколько миллилитров составляет объём стакана?
Ответ: 230.

5
Решение. Стакан пессимиста полон на 40%, а оптимиста — на 60%. У пессимиста, по срав- нению с оптимистом, воды меньше на 20% всего объёма стакана, т. е. на
1 всего объёма. Поскольку эта разность по условию составляет 46 миллилитров, весь объём стакана равен 46 ⋅ 5 = 230 миллилитров.
Задача 8.2. На доске нарисованы 23 знака — несколько плюсов и несколько минусов. Если среди них выбрать 10 любых знаков, то среди них точно окажется хотя бы один плюс. Если же среди них выбрать 15 любых знаков, то среди них точно окажется хотя бы один минус. Сколько всего плюсов выписано?
Ответ: 14.
Решение. Поскольку среди любых 10 знаков есть плюс, то минусов на доске не больше 9
(иначе можно было бы выбрать 10 минусов).
Поскольку среди любых 15 знаков есть минус, то плюсов на доске не больше 14 (иначе можно было бы выбрать 15 плюсов).
 Тогда всего знаков на доске не больше 9 + 14 = 23. Поскольку их по условию ровно 23, получаем, что минусов на доске ровно 9, а плюсов — ровно 14.
Тогда всего знаков на доске не больше 9 + 14 = 23. Поскольку их по условию ровно 23, получаем, что минусов на доске ровно 9, а плюсов — ровно 14.
Задача 8.3. В роще живут 140 хамелеонов — синие и красные. Однажды несколько си- них хамелеонов изменили свой окрас на красный. Тогда число синих хамелеонов умень- шилось в 5 раз, а число красных увеличилось в 3 раза. Сколько хамелеонов изменило свой окрас?
Ответ: 80.
Решение. Пусть синих хамелеонов стало 𝑥. Тогда изначально синих хамелеонов было 5𝑥. Соответственно, красных хамелеонов изначально было 140 − 5𝑥. Тогда красных хамелео- нов стало 3 ⋅ (140 − 5𝑥). Поскольку общее количество хамелеонов сохранилось, получаем уравнение
𝑥 + 3 ⋅ (140 − 5𝑥) = 140.
 Решая его, находим 𝑥 = 20. Тогда цвет изменили 5𝑥−𝑥 = 4𝑥 = 4 ⋅ 20 = 80 хамелеонов.
Решая его, находим 𝑥 = 20. Тогда цвет изменили 5𝑥−𝑥 = 4𝑥 = 4 ⋅ 20 = 80 хамелеонов.
Задача 8.4. Дан квадрат 𝐴𝐵𝐶𝐷. Точка 𝐿 на стороне 𝐶𝐷 и точка 𝐾 на продолжении сторо- ны 𝐷𝐴 за точку 𝐴 таковы, что ∠𝐾𝐵𝐿 = 90∘. Найдите длину отрезка 𝐿𝐷, если 𝐾𝐷 = 19 и
𝐶𝐿 = 6.
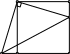
𝐵 𝐶
𝐿
𝐾
𝐴 𝐷
Ответ: 7.
Решение. Поскольку 𝐴𝐵𝐶𝐷 — квадрат, то 𝐴𝐵 = 𝐵𝐶 = 𝐶𝐷 = 𝐴𝐷.

𝐵 𝐶
𝐿
𝐾
𝐴 𝐷
Рис. 1: к решению задачи 8.4
Заметим, что ∠𝐴𝐵𝐾 = ∠𝐶𝐵𝐿, поскольку они оба дополняют ∠𝐴𝐵𝐿 до 90∘. Тогда прямо- угольные треугольники 𝐴𝐵𝐾 и 𝐶𝐵𝐿 равны по острому углу и катету 𝐴𝐵 = 𝐵𝐶 (рис. 1). Следовательно, 𝐴𝐾 = 𝐶𝐿 = 6. Тогда
 𝐿𝐷 = 𝐶𝐷 − 𝐶𝐿 = 𝐴𝐷 − 𝐶𝐿 = (𝐾𝐷 − 𝐴𝐾) − 𝐶𝐿 = 𝐾𝐷 − 2 ⋅ 𝐶𝐿 = 19 − 2 ⋅ 6 = 7.
𝐿𝐷 = 𝐶𝐷 − 𝐶𝐿 = 𝐴𝐷 − 𝐶𝐿 = (𝐾𝐷 − 𝐴𝐾) − 𝐶𝐿 = 𝐾𝐷 − 2 ⋅ 𝐶𝐿 = 19 − 2 ⋅ 6 = 7.
Задача 8.5. Есть 7 абсолютно одинаковых кубиков, у каждого из которых на одной грани отмечена 1 точка, на другой — 2 точки, …, на шестой — 6 точек. Причём на любых двух противоположных гранях суммарно отмечено 7 точек.
Из этих 7 кубиков сложили фигуру, изображённую на рисунке, так, что на каждой паре склеенных граней отмечено одинаковое количество точек. На всех гранях, кроме девяти, все точки стёрли, как показано на рисунке. Какое суммарное количество точек изначаль- но было отмечено на поверхности фигуры?

Ответ: 75.
Решение. Есть 9 способов отрезать от нашей фигуры «кирпичик», состоящий из двух ку- биков 1 × 1 × 1. В каждом таком «кирпичике» есть две противоположные грани 1 × 1, расстояние между которыми равно 2. Поставим эти две грани в соответствие друг к дру- гу.
Рассмотрим одну такую пару граней: на одной из них не стёрли точки, а на другой — стёрли. При этом, как нетрудно понять, первоначально на этих гранях было одинаковое количество точек.
Посчитаем суммарное количество точек, которое было на всех 9 парах граней первона- чально. Получается
2 ⋅ (1 + 1 + 6 + 2 + 2 + 5 + 3 + 3 + 4) = 54.
Осталось 6 граней 1 × 1, про которые нам до сих пор ничего неизвестно. Но можно заме- тить, что они разбиваются на пары по следующему принципу: в одной паре будут нахо- дится грани из одного кубика 1 × 1 × 1. В каждой такой паре сумма чисел была равна 7. Тогда получаем, что количество точек на поверхности фигуры первоначально было рав- но
 54 + 3 ⋅ 7 = 75.
54 + 3 ⋅ 7 = 75.
Задача 8.6. Вася задумал три натуральных числа с суммой 1003. Вычислив их произведе- ние, Вася заметил, что оно заканчивается на 𝑁 нулей. Какое наибольшее значение может
принимать 𝑁?
Ответ: 7.
Решение. Произведение трёх задуманных чисел могло заканчиваться на 7 нулей, напри- мер, если это были числа 625, 250, 128. Действительно, 625 + 250 + 128 = 1003 и
625 ⋅ 250 ⋅ 128 = 54 ⋅ (2 ⋅ 53) ⋅ 27 = 28 ⋅ 57 = 2 ⋅ 107 = 20000000.
 Предположим, существуют три натуральных числа с суммой 1003, произведение кото- рых заканчивается хотя бы на 8 нулей. Это означает, что оно делится на 108 = 28 ⋅ 58. Поскольку сумма всех трёх чисел не делится на 5, то какое-то из них не делится на 5. Тогда произведение двух других делится на 58. Тогда либо какое-то из них делится на 55 (что невозможно, ведь иначе общая сумма трёх чисел больше 55 = 3125 1003), либо они оба делятся на 54 (что также невозможно, ведь иначе общая сумма трёх чисел больше 54 + 54 = 625 + 625 1003). Противоречие.
Предположим, существуют три натуральных числа с суммой 1003, произведение кото- рых заканчивается хотя бы на 8 нулей. Это означает, что оно делится на 108 = 28 ⋅ 58. Поскольку сумма всех трёх чисел не делится на 5, то какое-то из них не делится на 5. Тогда произведение двух других делится на 58. Тогда либо какое-то из них делится на 55 (что невозможно, ведь иначе общая сумма трёх чисел больше 55 = 3125 1003), либо они оба делятся на 54 (что также невозможно, ведь иначе общая сумма трёх чисел больше 54 + 54 = 625 + 625 1003). Противоречие.
Задача 8.7. Про четырёхугольник 𝐴𝐵𝐶𝐷 известно, что ∠𝐵𝐴𝐶 = ∠𝐶𝐴𝐷 = 60∘, 𝐴𝐵 + 𝐴𝐷 =
𝐴𝐶. Также известно, что ∠𝐴𝐶𝐷 = 23∘. Сколько градусов составляет угол 𝐴𝐵𝐶?
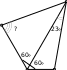
𝐶
𝐵
Ответ: 83.
𝐴 𝐷
Решение. Отметим на луче 𝐴𝐵 такую точку 𝐾, что 𝐴𝐾 = 𝐴𝐶. Тогда треугольник 𝐾𝐴𝐶 рав- носторонний; в частности, ∠𝐴𝐾𝐶 = 60∘ и 𝐾𝐶 = 𝐴𝐶. При этом 𝐵𝐾 = 𝐴𝐾 − 𝐴𝐵 = 𝐴𝐶 − 𝐴𝐵 =
𝐴𝐷. Это означает, что треугольники 𝐵𝐾𝐶 и 𝐷𝐴𝐶 равны по двум сторонам и углу 60∘ между ними (рис. 2).
 Осталось заметить, что угол 𝐴𝐵𝐶 — внешний для треугольника 𝐵𝐾𝐶 — равен внешнему углу при вершине 𝐷 треугольника 𝐷𝐴𝐶, который вычисляется как сумма двух внутрен- них: 60∘ + 23∘ = 83∘.
Осталось заметить, что угол 𝐴𝐵𝐶 — внешний для треугольника 𝐵𝐾𝐶 — равен внешнему углу при вершине 𝐷 треугольника 𝐷𝐴𝐶, который вычисляется как сумма двух внутрен- них: 60∘ + 23∘ = 83∘.
Задача 8.8. В футбольном турнире участвовали команды 𝐴, 𝐵, 𝐶, 𝐷, 𝐸. Каждая команда сыграла с каждой ровно один раз. В каждой игре за победу давалось 3 очка, за ничью — 1 очко, за поражение — 0 очков.
Известно, что по окончании турнира

𝐾
𝐶
𝐴 𝐷
Рис. 2: к решению задачи 8.7
все команды набрали разное количество очков;
команда 𝐴 набрала больше всех очков, хотя и проиграла команде 𝐵;
команды 𝐵 и 𝐶 не проиграли ни одной игры;
команда 𝐶 набрала меньше очков, чем команда 𝐷. Сколько очков набрала каждая из команд?
Команда 𝐴 набрала:
Команда 𝐵 набрала:
Команда 𝐶 набрала:
Команда 𝐷 набрала:
Команда 𝐸 набрала:
Ответ: Команда 𝐴 набрала 7 очков, 𝐵 — 6, 𝐶 — 4, 𝐷 — 5, 𝐸 — 2.
Решение. Будем обозначать количество очков команд 𝐴, 𝐵, 𝐶, 𝐷, 𝐸 за 𝑎, 𝑏, 𝑐, 𝑑, 𝑒 соответ- ственно.
Всего было сыграно 10 матчей. За матч, в котором одна из команд победила, в общую сумму всех очков добавляется 3 очка, а за ничейную игру — 2 очка. Следовательно, общая сумма очков всех команд получится, если из 30 вычесть количество ничейных матчей.
Команда 𝐶 не проиграла ни одного матча, поэтому набрала 𝑐 ⩾ 4 очков. А команда 𝐵 кроме того, что не проиграла ни одного матча, ещё и выиграла у команды 𝐴, поэтому набрала 𝑏 ⩾ 6 очков.
Покажем, что команда 𝐶 набрала ровно 4 очка. Предположим, что это не так, тогда она хотя бы один раз выиграла и набрала 𝑐 ⩾ 6 очков. По условию команды 𝐴 и 𝐷 набрали больше очков, чем команда 𝐶, тогда 𝑎 𝑑 6. Четыре числа 𝑎, 𝑏, 𝑐, 𝑑 различны и не меньше 6, следовательно, 𝑎 + 𝑏 + 𝑐 + 𝑑 ⩾ 6 + 7 + 8 + 9 = 30. Но все команды в сумме могут
набрать максимум 30 очков, причём только в том случае, если ничьих не было. Получаем, что тогда команды набрали ровно 0, 6, 7, 8, 9 очков, при этом ни разу не сыграв вничью. Получаем противоречие, ведь набрать 7 очков без ничьих невозможно.
Следовательно, команда 𝐶 набрала ровно 4 очка, то есть все 4 игры сыграла вничью. Ко- манда 𝐴 проиграла команде 𝐵, а также сыграла вничью с командой 𝐶, поэтому она на- брала не больше 7 очков. Поскольку 6 ⩽ 𝑏 , то 𝑏 = 6 и 𝑎 = 7. Причём это возможно только в том случае, когда команда 𝐴 выиграла у команд 𝐷 и 𝐸, а команда 𝐵 сыграла вни- чью со всеми, кроме 𝐴.
 Осталось понять, что команда 𝐷 должна была выиграть у команды 𝐸, чтобы набрать боль- ше, чем 𝐶. Тогда команда 𝐷 набрала 5 очков (выиграв у 𝐸 и сыграв вничью с 𝐵 и 𝐶), а команда 𝐸 — 2 очка (сыграв вничью с 𝐵 и 𝐶).
Осталось понять, что команда 𝐷 должна была выиграть у команды 𝐸, чтобы набрать боль- ше, чем 𝐶. Тогда команда 𝐷 набрала 5 очков (выиграв у 𝐸 и сыграв вничью с 𝐵 и 𝐶), а команда 𝐸 — 2 очка (сыграв вничью с 𝐵 и 𝐶).








 𝐵 𝐶
𝐵 𝐶  𝐵 𝐶
𝐵 𝐶 
 𝐶
𝐶  𝐾 𝐶
𝐾 𝐶 









