Разбор типовых заданий № 11 ЕГЭ по математике базового уровня

Разбор типовых заданий № 11 ЕГЭ по математике базового уровня

Геометрия

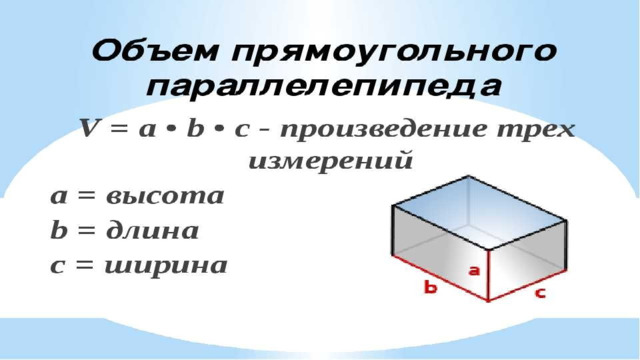
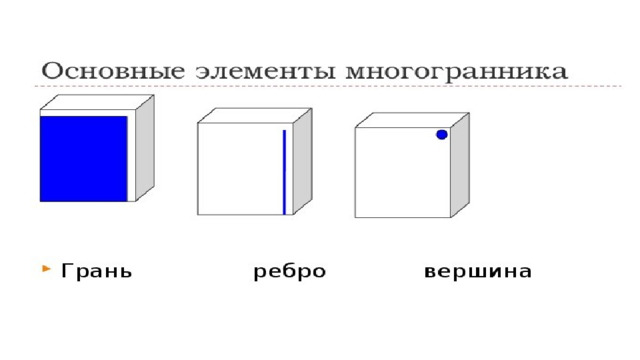
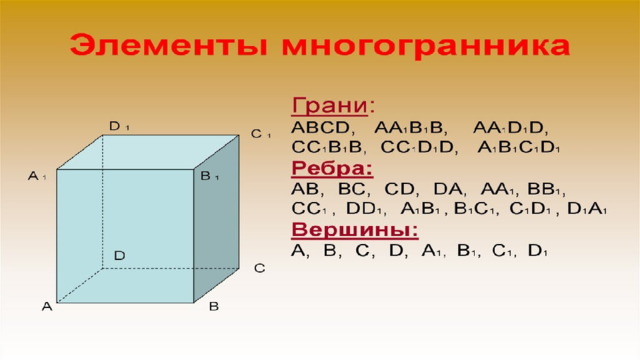
10. Даны две коробки, имеющие форму правильной четырёхугольной призмы. Первая коробка в четыре с половиной раза выше второй, а вторая втрое шире первой. Во сколько раз объём первой коробки меньше объёма второй?

V 1  = a 1  · b 1  · c 1

V 2  = a 2  · b 2  · c 2

Найдем отношение объемов.

V 1  / V 2  = (a 1  · b 1  · c 1 )/ ( a 2  · b 2  · c 2 )

По условию c 1  = 4,5 c 2  (первая коробка в четыре с половиной раза выше второй),

b 2  = 3 b 1  (вторая коробка втрое шире первой).

Так как это правильные четырехугольные призмы, то в основании лежит квадрат, а значит глубина второй коробки тоже втрое больше глубины первой, то есть a 2  = 3 a 1

Подставим эти выражения в формулу отношения объемов:

V 1  / V 2  = (a 1  · b 1  · c 1 )/ ( a 2  · b 2  · c 2 ) = (a 1  · b 1  · 4,5c 2 )/ ( 3a 1  · 3b 1  · c 2 ) = (a 1  · b 1  · 4,5c 2 )/ ( 9a 1  · b 1  · c 2 )

Сократим получившуюся дробь на a 1  · b 1  · c 2 . Получим:

V 1  / V 2  = (a 1  · b 1  · 4,5c 2 )/ ( 9a 1  · b 1  · c 2 ) = 4,5/9 = ½.

Объем первой коробочки в 2 раза меньше объема второй.

Ответ: 2.

! Алгоритм выполнения:

• Записать формулу, для вычисления объема правильной четырехугольной призмы.
• Записать в общем виде формулу для нахождения объема в первом и втором случае.
• Найти отношение объемов.
• Преобразовать полученное выражение с учетом соотношения измерений первой и второй призмы.
• Сократить получившуюся дробь.

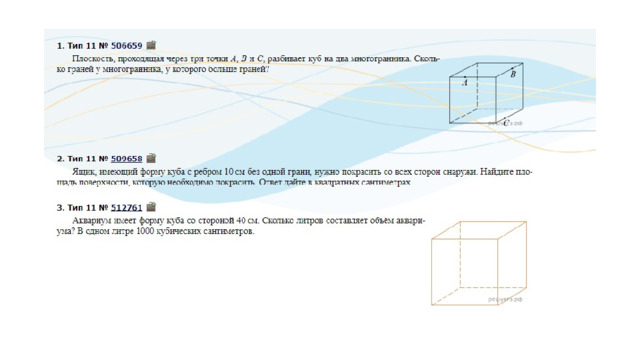
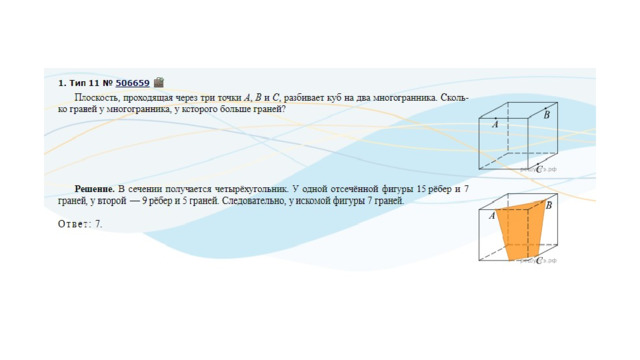
11. От деревянного кубика отпилили все его вершины (см. рис.). Сколько граней у получившегося многогранника (невидимые ребра на рисунке не изображены)?

! Сначала вспомним сколько всего граней и вершин у куба: шесть граней и восемь вершин. Теперь на месте каждой вершины образуется новая грань после отпила, значит у модифицированного в задании куба шесть родных граней и восемь новых (после отпила). Итого получаем: 6 + 8 = 14 граней.

Ответ: 14.

Если бы нас спросили, а сколько вершин у нового «куба». Очевидно, если вместо одной становится три, а их всего восемь, то получаем: 8 • 3 = 24

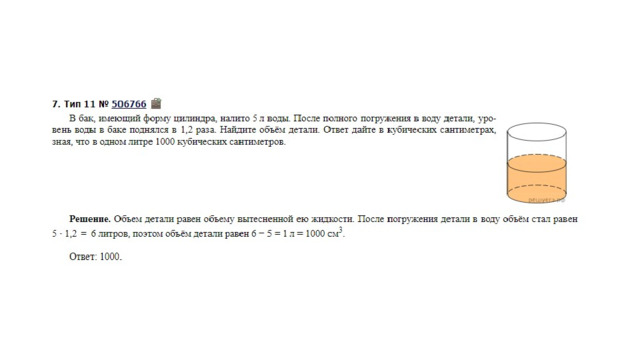
13. В бак, имеющий форму прямой призмы, налито 5 л воды. После полного погружения в воду детали уровень воды в баке поднялся в 1,4 раза. Найдите объем детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.

! Алгоритм выполнения

• Вводим обозначения для объема до погружения детали и после. Пусть это будет соответственно  V 1  и  V 2 .
• Фиксируем значение для  V 1 . Выражаем  V 2  через  V 1 . Находим значение  V 2 .
• Переводим результат, полученный в литрах, в куб.см.

Объем бака до погружения  V 1 =5 (л). Т.к. после погружения детали объем стал равным  V 2 . Согласно условию, увеличение составило 1,4 раза, поэтому  V 2 =1,4 V 1 .

Отсюда получаем:  V 2 =1,4·5=7 (л).

Т.о., разница объемов, которая и составляет объем детали, равна:

V 2 –V 1 =7–5=2 (л).

2 л=2·1000=2000 (куб.см).

14. В сосуде, имеющем форму конуса, уровень жидкости достигает ½ высоты. Объем сосуда 1600 мл. Чему равен объем налитой жидкости? Ответ дайте в миллилитрах.

Если рассматривать сечение конуса по двум его противоположно расположенным образующим (осевое сечение), то видим, что полученные таким способом треугольники большого конуса и малого (образованного жидкостью) подобны. Это следует из равенства их углов. Т.е. имеем: у конусов подобны высоты и радиусы основания. Отсюда делаем вывод: т.к. линейные параметры конусов подобны, то и конусы подобны.

По условию высота малого конуса (жидкости) составляет ½ высоты конуса. Значит, коэффициент подобия малого и большого конусов равен ½.

Применяем св-во подобия тел, которое заключается в том, их объемы относятся как коэффициет подобия в кубе. Обозначим объем большого конуса  V 1 , малого –  V 2 . Получим:

! Алгоритм выполнения

• Доказываем, что данные в условии конусы подобны.
• Определяем коэффициент подобия.
• Используя свойство для объемов подобных тел, находим объем жидкости.

Поскольку по условию  V 1 =1600 мл, то  V 2 =1600/8=200 мл.

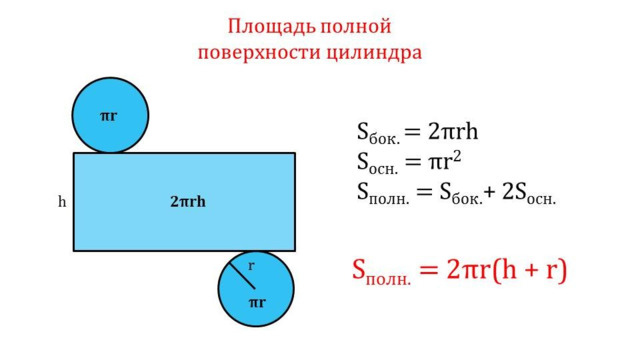
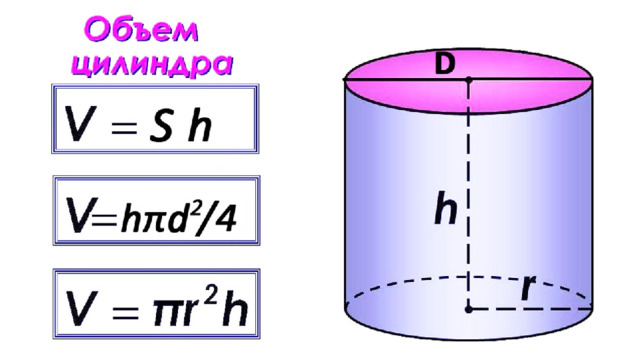
16. Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 4 и 18, а второго – 2 и 3. Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности второго?

! Алгоритм выполнения

• Записываем формулу для определения площади бок.поверхности цилиндра.
• Переписываем ее дважды с использованием соответствующих индексов – для 1-го (большего) и 2-го (меньшего) цилиндров.
• Находим отношение площадей. Вычисляем отношения, используя числовые данные из условия.

Вывод: площадь боковой поверхности 1-го цилиндра больше в 12 раз.

9. Вода в сосуде цилиндрической формы находится на уровне h = 80 см. На каком уровне окажется вода, если ее перелить в другой цилиндрический сосуд, у которого радиус основания в 4 раза больше, чем у данного? Ответ дайте в сантиметрах.

V 1  = π r 1   2  h 1

V 2  = π r 2   2  h 2

Объем жидкости не изменялся, следовательно, можно приравнять объемы.

V 1  = V 2

π r 1   2  h 1  = π r 2   2  h 2

h 2  =( π r 1   2  h 1 )/ π r 2   2

По условию площадь основания стала в 4 раза больше, то есть r 2  = 4 r 1  .

Подставим r 2  = 4 r 1  в выражение для h 1.

Получим: h 2  =( π r 1   2  h 1 )/ π (4 r 1 )  2

Полученную дробь сократим на π, получим h 2  =( r 1   2  h 1 )/ 16 r 1   2

Полученную дробь сократим на r 1 , получим h 2  = h 1 / 16.

Подставим известные данные: h 2  = 80/ 16 = 5 см.

Ответ: 5.

! Алгоритм выполнения:

• Записать формулу объема цилиндра.
• Подставить значения для цилиндра с жидкостью в первом и во втором случае.
• Объем жидкости не изменялся, следовательно, можно приравнять объемы.
• Полученное уравнение решить относительно второй высоты h 2 .
• Подставить данные и вычислить искомую величину.

12. Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 2 и 6, а второго – 6 и 4. Во сколько раз объем второго цилиндра больше объема первого?

V 1 =πR 1 2 H 1 ,

V 2 =πR 2 2 H 2 .

! Алгоритм выполнения

• Записываем ф-лу для вычисления объема цилиндра.
• Вводим обозначения для радиуса основания и высоты 1-го цилиндра. Выражаем подобным образом аналогичные параметры 2-го цилиндра.
• Формируем формулы для объема 1-го и 2-го цилиндров.
• Вычисляем отношение объемов.