План занятия № 3-4 (4 часа)
Дата проведения занятия _______________г.
Группа:
Преподаватель Любарь Ольга Васильевна
Раздел 7. Информация и информационные процессы.
Тема: «Представления информации. Системы счисления»
Цели занятия:
образовательные: формирование и развитие знаний о дискретном представлении информации и системах счисления;
формирование и развитие умений обработки двоичной системы счисления;
развивающая: развитие познавательного интереса, логического мышления, речи и внимания учащихся, формирование информационной культуры и потребности приобретения знаний;
воспитательная: привитие учащимся навыка самостоятельности в работе, воспитание трудолюбия, эстетического отношения к результатам своего труда.
Задачи занятия:
- познакомить учащихся с основными понятиями представления информации и двоичной системой счисления;
-познакомить с достоинствами дискретного представления информации;
-показать на примерах перевод чисел из одной системы счисления в другую:
-объяснить алгоритм перевода чисел из десятеричной системы в двоичную;
-научить переводу чисел в двоичную систему счисления разными способами;
-познакомить с алгоритмом Горнера;
-научить выполнению алгоритма Горнера.
УМК:
- презентация:
«Дискретные и непрерывные сигналы»,
Оборудование:
Интерактивная доска,
Персональные компьютеры
ХОД ЗАНЯТИЯ
Этапы занятия:
1.Организационный момент
2. Проверка домашнего задания
3. Изложение нового материала (теоретические сведения):
Универсальность дискретного представления информации
Двоичная система счисления
Физкультминутка
Физкультминутка
4. Закрепление изученного материала
5. Итоги занятия
6. Домашнее занятие
Организационный момент
Давайте поприветствуем друг друга. Здравствуйте! Присаживайтесь. Приготовьтесь к занятию.
Проверка домашнего задания
Вопросы:
-Что такое информация?
-Какие свойства информации вы знаете?
-Что такое мера информации?
-Что такое количество информации?
-Какие единицы информации вы знаете?
-Что такое информационный объект?
-Виды информационных объектов?
3. Изложение нового материала
(Теоретические сведения к практической работе)
Универсальность дискретного представления информации
Существует два принципиально отличных способа представления информации: непрерывный и дискретный. Если некоторая величина, несущая информацию, в пределах заданного интервала может принимать любое значение, то она называется непрерывной. Наоборот, если величина способна принимать только конечное число значений в пределах интервала, она называется дискретной. Для наглядного представления о сути явления дискретности можно также сравнить таблицу значений функции и ее график, полученный путем соединения соответствующих точек плавной линией.
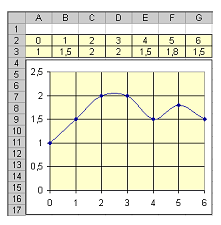
Очевидно, что с увеличением количества значений в таблице (интервал дискретизации сокращается) различия существенно уменьшаются, и дискретизированная величина все лучше описывает исходную (непрерывную).
Наконец, когда имеется настолько большое количество точек, что мы не в состоянии различить соседние, на практике такую величину можно считать непрерывной.
Компьютер способен хранить только дискретно представленную информацию. Его память, как бы велика она ни была, состоит из отдельных битов, а значит, по своей сути дискретна.
Достоинства дискретного (цифрового) представления информации:
• простота
• удобство физической реализации
• универсальность представления любого вида информации
• уменьшение избыточности сообщения
• обеспечение защиты от случайных искажений или нежелательного доступа.
В компьютере для представления информации используется дискретное (цифровое) двоичное кодирование, так как удалось создать надежно работающие технические устройства, которые могут со стопроцентной надежностью сохранять и распознавать не более двух различных состояний (цифр)
Информация в компьютере представлена в двоичном коде, алфавит которого состоит из двух цифр – 0 и 1. Цифра двоичной системы называется битом (от английских слов binary digit – двоичная цифра).
Теоретической основой кодирования чисел является подробным образом развитая в математике теория систем счисления.
Каждый нормальный человек умеет записывать и читать числа, но редко кто задумывается, почему это делается именно так, а не по-другому. Как и многое другое в истории развития человечества, используемая нами форма записи чисел не была придумана сразу, а совершенствовалась в течение тысяч лет.
Система счисления – это способ представления чисел и соответствующие ему правила действия над числами. Разнообразные системы счисления, которые существовали раньше и которые используются в наше время, можно разделить на позиционные и непозиционные. Знаки используемые при записи чисел, называются цифрами.
В непозиционных системах счисления от положения цифры в записи числа не зависит величина, которую она обозначает.
Примером непозиционной системы счисления является римская система (римские цифры). В римской системе в качестве цифр используются латинские буквы: I – 1; V – 5; X – 10; L – 50; C – 100; D – 500; М – 1000.
В римских числах цифры записываются слева направо в порядке убывания. В таком случае их значения складываются. Если же слева записана меньшая цифра, а справа – большая, то их значения вычитаются.
Пример VI = 5 + 1 = 6, VI = 5 – 1 = 4.
MCMXCVIII = 1000 + (-100 + 1000) + (-10 + 100) + 5 + 1 + 1 + 1 = 1998.
В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от ее позиции. Количества используемых цифр называется основанием позиционной системы счисления.
Система счисления, применяемая в современной математике, является позиционной десятичной системой. Ее основание равно десяти, т.к. запись любых чисел производится с помощью десяти цифр:0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Позиционный характер этой системы легко понять на примере любого многозначного числа. Например в числе 333 первая тройка означает три сотни, вторая - три десятка, третья - три единицы.
Для записи чисел в позиционной системе счисления с основанием n нужно иметь алфавит из n цифр. Обычно для этого при n n 10 к десяти арабским цифрам добавляют буквы. Вот примеры алфавитов нескольких систем.
| Основание | Название | Алфавит |
| n = 2 | двоичная | 0 1 |
| n = 3 | троичная | 0 1 2 |
| n = 8 | восьмеричная | 0 1 2 3 4 5 6 7 |
| n = 16 | шестнадцатеричная | 0 1 2 3 4 5 6 7 8 9 A B C D E F |
Если указать основание системы, к которой относится число, то оно приписывается нижним индексом. Например: 1011012, 36718, 3B8F16
В системе счисления с основанием q (q–ичная система счисления) единицами разрядов служат последовательные степени числа q.
q единиц какого-либо разряда образуют единицу следующего разряда.
Для записи числа в q-ичной системе счисления требуется q различных знаков (цифр), изображающих цифры от 0, 1,…, q-1. Записать числа q в q-ичной системе счисления имеет вид 10.
Развернутой формой записи числа называется запись в виде
Aq = (a n-1q n-1 + a n-2q n-2 + … + a 0 q 0 + a-1 q -1+ a -2 q -2+ … + a-m q-m).
Здесь Aq – само число, q – основание системы счисления, ai –цифры данной системы счисления, n – число разрядов целой части числа, m – число разрядов дробной части числа.
Пример. Получить развернутую форму десятичных чисел 32478; 26,387. 32478 10 = 3 * 10000 + 2 * 1000 + 4 * 100 + 7 * 10 + 8 =
3 * 10 4 + 2 * 10 3 + 4 * 10 2 + 7 * 10 1 + 8 * 10 0
26,387 10 = 2 * 10 1 + 6 * 10 0 + 3 * 10 –1 + 8 * 10 –2 + 7 * 10 –3
Пример 6. Все числа 112 3, 1011012, 15FC16, 101,112
перевести в десятичную систему. 112 3 = 1 * 3 2 + 1 * 3 1 + 2 * 3 0 = 1410
1011012 = 1 * 2 5 + 0 * 2 4 + 1 * 2 3 + 1 * 2 2 + 0 * 2 1 + 1 * 2 0
15FC 16 = 1 * 16 3 + 5*16 2 + F * 16 1 + 12
101, 11 2 = 1 * 22 + 0 * 2 1 + 1 * 2 0 + 1* 2 –1 + 1* 2 –2
ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ
Вспомогательные вопросы
Как вы думаете, откуда взяла начало система счисления с основанием 20, которой пользовались некоторые народы тёплых районов земли? А система счисления с основанием 12 ?
Сколько цифр необходимо для записи чисел в системе счисления с основанием 6, с основанием 3, с основанием 2 ?
Знаете ли вы какие-нибудь славянские или греческие цифры ?
При каком арифметическом действии используются понятия делимое, делитель, частное, остаток, полное частное, неполное частное ? Приведите примеры.
Можете ли вы рассказать что-нибудь о приспособлениях, которые использует или когда-то использовало человечество для облечения вычислений ?
Десятичная система счисления неудобна для использования в электронных машинах. Дело в том, что техническая реализация устройств
для операций с десятичными числами является громоздкой, невыгодной и сложной. Намного проще и эффективнее использовать всего две цифры (0 и 1), потому что создавать соответствующую электрическую схему не составляет труда, например, “отключено” – 0, а “высокое напряжение” – 1; “низкое напряжение” – 0, а “высокое напряжение “ – 1.
Система счисления с основанием 2, в которой используются всего 2 цифры, называется двоичной системой счисления, или бинарной, от английского слова binary (байнери – двоичный).
Электронной машине удобно работать с числами, записанными с помощью только двух цифр, т. е. В двоичной системе счисления. Но, чтобы человек, работающий с десятичной системой, и компьютер, работающий с двоичной системой, “понимали” друг друга, необходимо уметь переводить десятичную запись в двоичную, а двоичную - в десятичную.
Это делается очень просто. Но сначала вспомним несколько математических понятий, которые применяются при делении одного натурального числа на другое:
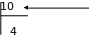 делимое
делимое  45
45
40
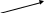 5
5
делитель
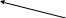 частное
частное
остаток
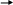
 4510 Х2 - ? Х2 = 1011012
4510 Х2 - ? Х2 = 1011012

45
2  44 22 2
44 22 2
Для перевода из десятичной системы счисления в двоичную необходимо:

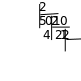
1
22 
11
разделить число на 2 (основание двоичной системы счисления);

зафиксировать остаток системы счисления 0 или 1 и частное от деления; если частное не равно 0, то разделить его на 2 и так далее;
если частное = 0, то записать все полученные остатки, начиная с последнего слева направо.
Аналогично, чтобы записать число в любой другой системе счисления, необходимо воспользоваться схемой получения цифр числа, только делителем будет не число 10, а основание нужной системы счисления, например, число 3.
Число, записанное в двоичной системе, можно легко сохранить в электронной машине.
Для хранения одного двоичного разряда применяется специальное устройство – триггер, название которого происходит от английского слова trigger (триггер – защёлка, переключатель). Триггер может находиться в двух устойчивых состояниях – “отключён”, что соответствует цифре 0, и “включён”, что соответствует цифре 1.
Для перевода числа из двоичной системы в десятичную достаточно вспомнить разложение числа 457810 в виде суммы :
* 103 + 5 * 102 + 7 * 101 + 8 * 100, где 10 – основание системы счисления, а показатели при числе 10 – номера цифр.
Аналогично распишем, например, число 1011012 ⟶ X10 ?
4 3 2 1 0
101101 = 1·25 + 0·24 + 1·23 + 1·22 + 0·21 + 1·20 = 32 + 0 + 8 + 4 + 0 +1 = 45
Переведите число 1110012 в десятичную систему счисления.
11101012 = 1 * 26 + 1 * 25 + 1 * 24 + 0 * 23 + 1 * 22 + 0 * 20 = 64 + 32 + 16 + 0 + 4
+ 0 + 1 = 11710
Ответ: 11101012 = 11710
ВОСЬМЕРИЧНАЯ И ШЕСТНАДЦАТЕРИЧНАЯ СИСТЕМЫ СЧИСЛЕНИЯ
Общение с компьютером на языке двоичных чисел слишком неудобно. Представьте себе лист бумаги, а на нём написаны сотни и тысячи нулей и единиц, которые необходимо записать в ЭВМ! Мало того, что на эту работу уйдёт огромное время, но гораздо больше придётся потратить на поиск и исправление неизбежных ошибок. Для облегчения работы с двоичными числами создали использовать в качестве вспомогательного средства систему счисления с снованием восемь и шестнадцать. 8 и 16 – есть степени двойки, а значит перевод между ними и двоичной системой максимально прост.
8 = 23 16 = 24
Это значит, что восьмеричная цифра объединяет ровно 3 двоичных разряда, а шестнадцатеричная – 4.
Алгоритм перевода из двоичной системы счисления в восьмеричную (шестнадцатиричную).
Сгруппировать двоичные разряды справа налево по три (четыре); если в старшей (т. е. самой левой) группе битов не хватает,то их можно дополнить слева незначащими нулями.
Заменить каждую из полученных групп соответствующей ей восьмеричной (шестандцатеричной) цифрой.
110102 ⟶ 011 0102 = 110102 ⟶ 0001 1010 = 1А16
Обратный переход еще проще: достаточно каждую восьмеричную (шестнадцатеричную) цифру заменить ее двоичным представлением,
дополняя его при необходимости до трех (четырех) двоичных цифр нулями слева
7DF = 0111 1101 1111
7 D F
Для записи шестнадцатеричных чисел необходимо 16 цифр. Первые десять цифр – это арабские цифры, а остальные шесть цифр – это первые буквы латинского алфавита: A, B, C, D, E, F:
| Десятичная | Двоичная | Восьмеричная | Двоичная | Шестнадцатиричная |
| 0 | 000 | 0 | 0000 | 0 |
| 1 | 001 | 1 | 0001 | 1 |
| 2 | 010 | 2 | 0010 | 2 |
| 3 | 011 | 3 | 0011 | 3 |
| 4 | 100 | 4 | 0100 | 4 |
| 5 | 101 | 5 | 0101 | 5 |
| 6 | 110 | 6 | 0110 | 6 |
| 7 | 111 | 7 | 0111 | 7 |
| 8 | 1000 |
| 1000 | 8 |
| 9 | 1001 |
| 1001 | 9 |
| 10 | 1010 |
| 1010 | A |
| 11 | 1011 |
| 1011 | B |
| 12 | 1100 |
| 1100 | C |
| 13 | 1101 |
| 1101 | D |
| 14 | 1110 |
| 1110 | E |
| 15 | 1111 |
| 1111 | F |
Используя эту таблицу, можно легко переводить восьмеричные (шестнадцатеричные) числа в двоичные и обратно.
ПЕРЕВОД ДЕСЯТИЧНЫХ ЧИСЕЛ В ДРУГИЕ СИСТЕМЫ СЧИСЛЕНИЯ
Перевод целых чисел.
Основание новой системы счисления выразить в десятичной системе счисления и все последующие действия производить в десятичной системе счисления;
Последовательно выполнять деление данного числа и получаемых неполных частных на основании новой системы счисления до тех пор, пока не получим неполное частное, меньшее делителя;
Полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;
Составить число в новой системе счисления, записывая его начиная с последнего остатка.
Перевод дробных чисел
Основание новой системы счисления выразить в десятичной системе счисления и все последующие действия производить в десятичной системе
счисления;
Последовательно умножать данное число и получаемые дробные части произведений на основание новой системы до тех пор, пока дробная часть произведения не станет равной нулю или не будет достигнута требуемая точность представления числа в новой системе счисления;
Полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;
Составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения.

| 0 | 1875 * 2 |
| 0 | 3750 * 2 |
| 0 | 7500 * 2 |
Пример: Перевести десятичную дробь 0,1875 в двоичную и восьмеричную системы.
| 0 | 1875 * 8 |
| 1 | 5000 |
|
| * 8 |
| 4 |
| 0000 |
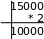
Вертикальная черта отделяет целые части чисел от дробных частей. 0,187510 = 0,00112; 0,187510 = 0,148
Пример:
Физкультминутка
Схема Горнера
При вычислении десятичного значения р-ичного целого числа по развернутой форме
удобно пользоваться схемой Горнера, которая позволяет минимизировать арифметические
операции и исключить возведение в степень.
Схема Горнера была на самом деле применена англичанином Горнером (а ещё
раньше итальянцем Руффини) для вычисления коэффициентов многочлена p(x+c) и
использовалась для приближённого вычисления корней многочленов. Еще одним
применением схемы Горнера является быстрый алгоритм перевода из двоичной системы в
десятичную, предложенный Соденом в 1953 году: старшую цифру умножаем на
основание, добавляем вторую цифру, результат умножаем на основание, добавляем третью
цифру и так до тех пор, пока не прибавим последнюю цифру.
Результатом будет десятичная запись числа. Полученное равенство будет
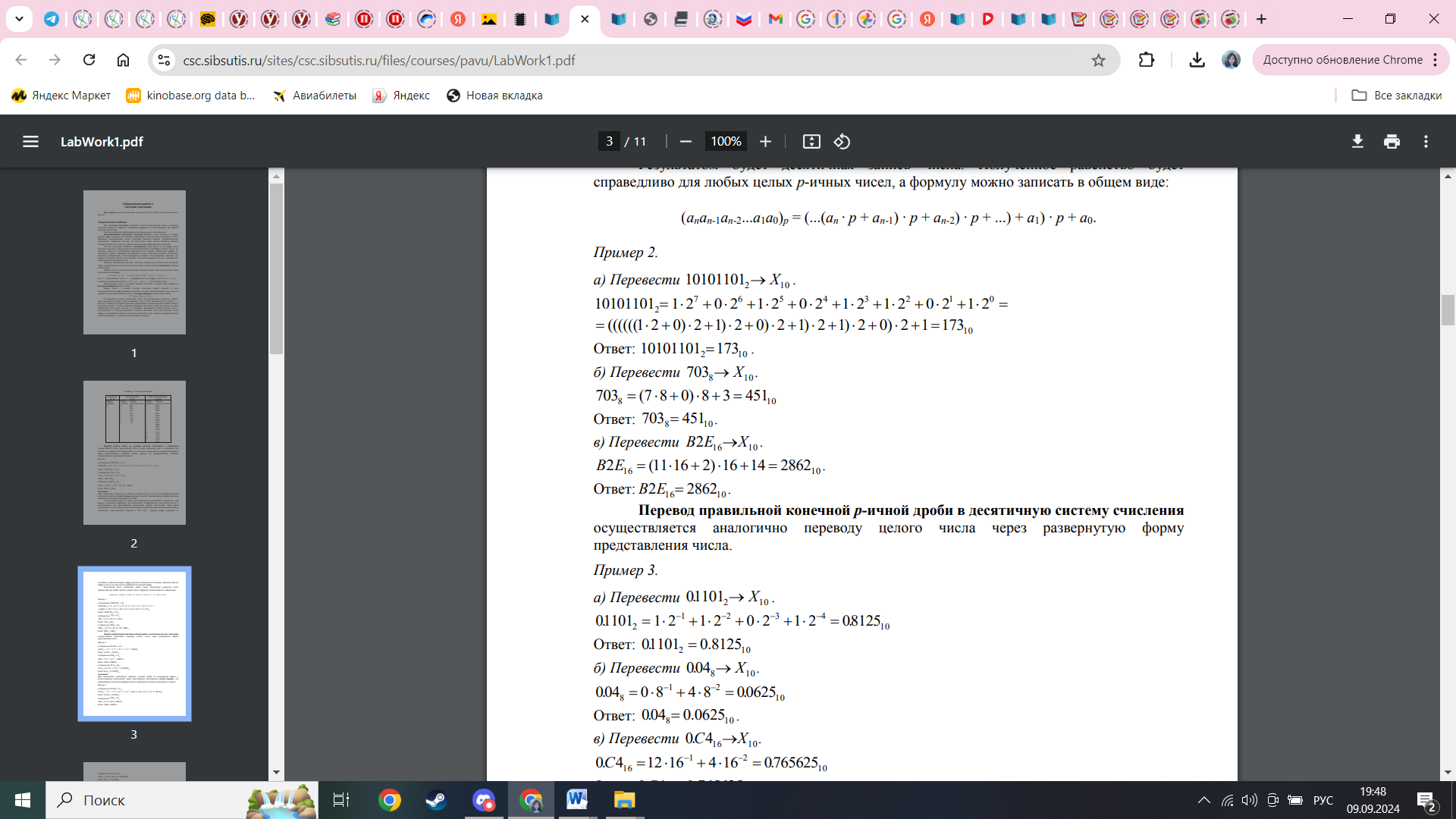
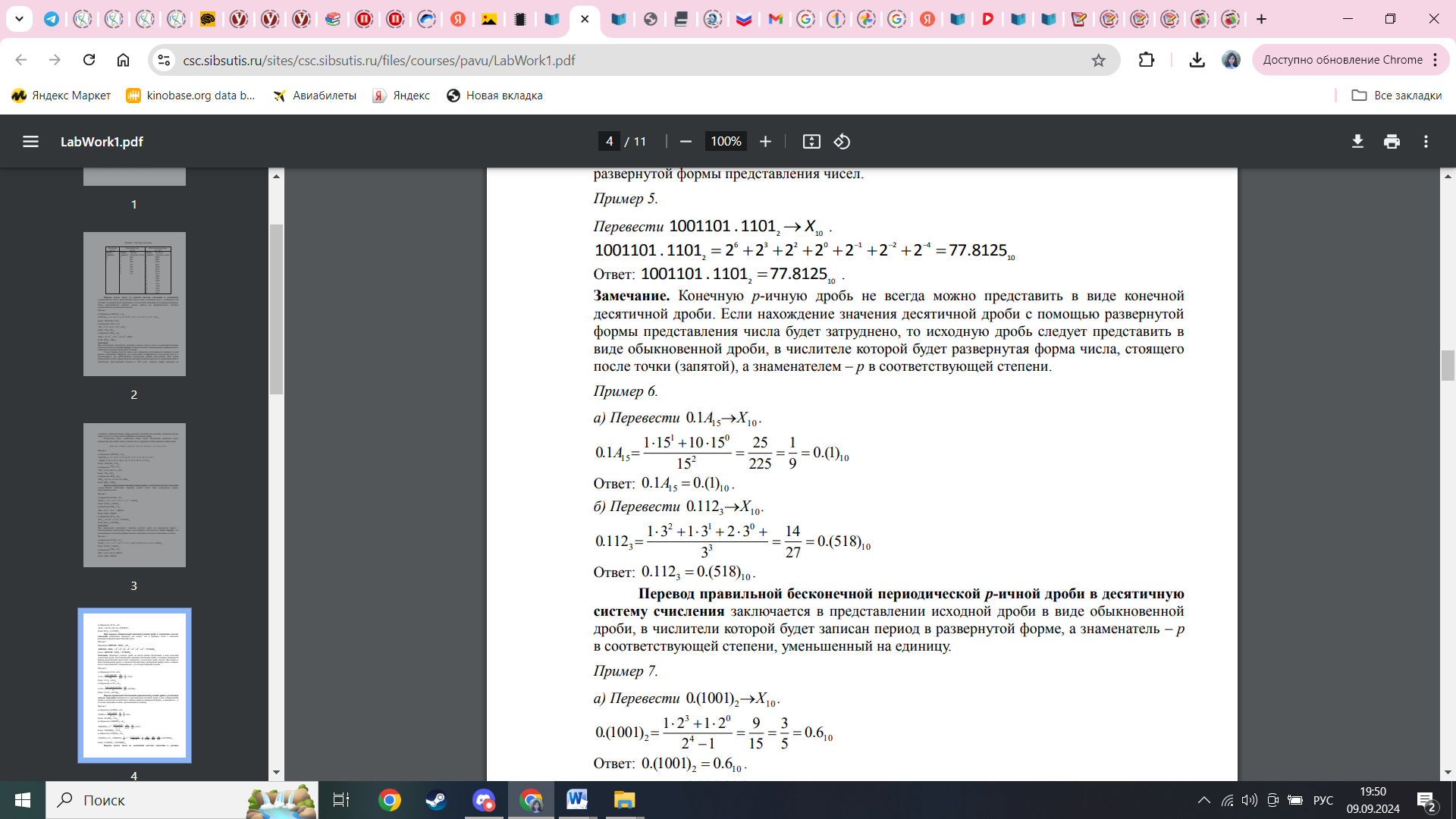
справедливо для любых целых p-ичных чисел, а формулу можно записать в общем виде:
(anan-1an-2...a1a0)p = (...(an ∙ p + an-1) ∙ p + an-2) ∙ p + ...) + a1) ∙ p + a0. 
| СХЕМА ГОРНЕРА AnPn+An-1Pn-1+……+A5P5+A4P4+A3P3+A2P2+A1P1+A0P0+…… |

Практические задания
Для 5 букв латинского алфавита заданы их двоичные коды (для некоторых букв – из двух бит, для некоторых – из трех).
Эти коды представлены в таблице:
| a | b | c | d | e |
| 000 | 110 | 01 | 001 | 10 |
Определите какой набор букв закодирован двоичной строкой 1100000100110
bade;
badde;
bacde;
bacdb.
Запишите следующие числа по схеме Горнера:
а). А10 =0,234 б). А10=0,342 в). А10=0,285
А10=5678 А10=6721 А10=4930
А10 =456,46 А10=364,72 А10=567,24
А10 =456,46 А10=364,72 А10=567,24
Задания
Выполните операцию сложения над двоичными числами:
а). 1) 10010011+101101 а). 1) 10110111+10011011
2) 1011101+11101101 2) 10010111+1011100
3) 11101001+10011101 3) 1101001 1+1 101 1011
4) 110010,11+110110,11 4) 111011,11+101111,11
в). 1). 11001110 +100010001 2). 10011110 + 10101010
3). 11001100 + 1011101 4). 110111,01 + 10011,11
Переведите целые числа из двоичной системы в десятичную по схеме Горнера:
а). 1) 110101110001110 2) 1001010011011101
3) 10110010010001010 4) 11000011010100000
б). 1) 11001010000111100 2) 11110001110011010
3) 11110101000101010 4) 11111010100100011
в). 1) 1011111000011111110 2) 10011110001111000
3) 1111001111001001101 4) 10011100110011100
5. Все числа 122 3, 1010012, 15FВ16, 101,012 перевести по схеме Горнера в десятичную систему счисления
6.Все 4-буквенные слова, составленные из букв Ш,К,О,Л,А. записаны в алфавитном порядке и пронумерованы. Вот начало списка:
1. АААА
2. АААК
3. АААЛ
4. АААО
5.АААШ
Запишите слова, которые стоит под номерами 11, 125, 348, 500, 563.
7. Все 5-буквенные слова, составленные из букв А, К, Р, У, записаны в алфавитном порядке. Вот начало списка:
1. ААААА
2. ААААК
3. ААААР
4. ААААУ
5. АААКА
……
Укажите номер слова УКАРА.
ТЕСТ ПО ТЕМЕ:
" Системы счисления"
В зависимости от способа изображения чисел системы счисления делятся на: а) арабские и римские;
б) позиционные и непозиционные;
в) представление в виде ряда и в виде разрядной сетки.
Двоичная система счисления имеет основание: а) 10; б) 8; в) 2.
Для представления чисел в шестнадцатеричной системе счисления используются:
а) цифры 0 - 9 и буквы А - F; б) буквы А - Q;
в) числа 0 - 15.
В какой системе счисления может быть записано число 402? а) в двоичной; б) в троичной; в) в пятеричной.
Чему равно число DXXVII в десятичной системе счисления? а) 527; б) 499; в) 474.
Недостатком позиционной системы счисления является: а) сложно выполнить арифметические операции;
б) ограниченное число символов, необходимых для записи числа; в) различное написание цифр у различных народов.
Даны системы счисления: 2-ая, 8-ая, 10-ая, 16-ая. Запись вида 352: а) отсутствует в двоичной системе счисления;
б) отсутствует в восьмеричной;
в) существует во всех названых системах счисления.
Какие цифры используются в шестеричной системе счисления? а) 0,6,5,2;
б) 8,6,1,0;
в) 0,3,2,1.
Какое минимальное основание должна иметь система счисления, если в ней можно записать числа: 341, 123, 222, 111.
а) 3; б) 4; в) 5.
Когда 2*2=11?
а) в двоичной системе счисления; б) в троичной системе счисления;
в) в четверичной системе счисления.
Как записывается максимальное 4-разрядное положительное число в троичной системе счисления?
а) 2222; б) 1111; в) 3333.
Цифры - это:
а) символы, участвующие в записи числа; б) буквы, участвующие в записи числа;
в) пиктограммы, участвующие в записи числа.
4. Закрепление изученного материала
Вопросы:
-Какие способы представления информации вы узнали на занятии?
-Что мы называем непрерывным представлением информации?
-Что мы называем дискретным представлением информации?
-Какие достоинства дискретного представления вы узнали на занятии?
-В каком коде представлена информация в компьютере?
-Как мы называем цифры двоичной системы?
-Что такое система счисления?
-На какие классы можно разделить все системы счисления?
-Что можно получить с помощью алгоритма Горнера?
5. Итоги занятия
Оценивается работа учащихся
6. Домашнее занятие
Выучит новые понятия
Литература
Информатика и ИКТ: учебник для начального и среднего профессионального образования. Цветкова Н.С., Великович Л.С. – Академия, 2011 г.
Информатика и ИКТ. Практикум для профессий и специальностей технического и социально-экономического профилей. Н. Е. Астафьева, С. А. Гаврилова, под ред. М.С. Цветковой, Академия, 2012г.
ПРИМЕЧАНИЕ
____________________________________________________________________________________
____________________________________________________________________________________
____________________________________________________________________________________
____________________________________________________________________________________
____________________________________________________________________________________








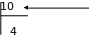 делимое
делимое 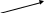 5
5 частное
частное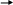
 4510 Х2 - ? Х2 = 1011012
4510 Х2 - ? Х2 = 1011012 45 2
45 2  44 22 2
44 22 2 
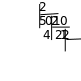 1 22
1 22 


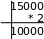




 Практические задания
Практические задания 









