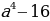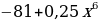Разложение многочленов на множители. Преобразование выражений

13/01

Урок алгебры в 7-А, 7-Б, 7-В классах

Тема урока: Разложение многочленов на множители. Преобразование выражений

Ребята, откройте рабочие тетради. Запишите:

Тринадцатое января

Классная работа

Разложение многочленов на множители. Преобразование выражений

Актуализация знаний

Вспомним, что:

Используя эти формулы и правило умножения многочленов можно преобразовывать различные алгебраические выражения и решать уравнения.

Разминка

Найдите квадраты и кубы выражений:

Решаем вместе:

Задача 1 Представьте в виде многочлена выражения:

а) (у² – 2а)(2а + у²);

б) (3х²+х)²;

в) (2 + т)²(2 – т)²;

г) .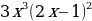

Задача 2. Выполните умножение многочленов:

1. ( x + 3)(x²–3x +9)

( x + 3)(x²–3x +9) = x³+ 3³= x³+ 27

1. (2x – 3y)(4x²+6xy + 9y²)

(2x – 3y)(4x²+6xy + 9y²) = (2x)³– (3y)³= 8x³–27y³.

Задача 3. Разложите многочлен на множители:

1. 

2. 

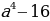
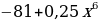
3. x³– 8 y³= x³– (2y)³= (x – 2y) (x²+2xy + 4y²)

4. 64 a ³+ 27c³= (4a)³+ (3c)³= (4a + 3c)(16a² – 12 ac + 9c²)

5. 9х² – 24х + 16.

Задача 4. Упростите выражение:

(x +2)(x²– 2x +4) – x(x–3)(x+3).

Решение:

x³+ 2³– x(x²– 9) = x³+ 8 – x³+ 9x = 8 + 9x.

Ответ: 8 + 9x.

Задача 5. Доказать, что выражение 123³+ 27³ кратно 50.

(Кратно 50 значит делится на 50).

Используем формулу:

a³+ b³= (a + b)(a²– ab + b²),

получим:

(123 + 27)(123²–123 · 27 + 27²) =150 · (123²–123 · 27 + 27²).

Произведение делится на 50, так как первый множитель делится на 50:

(150 : 50 = 3). Нет необходимости считать значение выражения в скобках. Утверждение доказано.

Домашнее задание:

1. Повторяем изученные формулы и правила

2. Выполняем задания:

1.Преобразовать в многочлен:

а) (а + 5)²; в) (2b – 1)(2b + 1);

б) (3y – x)²; г) (4a + 3b)(4a – 3b).

2. Разложить на множители:

а) b² – 16; в) 49a²b⁴ – 100c⁴;

б) a² + 6a + 9;

3. Упростить выражение:

(a – 3)² – 3a(a – 2).

4. Выполнить действия:

а) (x² + 1)(x – 1)(x + 1);

б) (x + 1)² + (x – 1)²
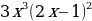