СТВ (7) Дата: 21.10.2024
Урок № 8
Тема урока: Числовые наборы Среднее арифметическое
Образовательная цель: Ввести понятие среднего арифметического массива данных: среднее арифметическое как его вычислить: рассмотреть среднее арифметическое как среднее значение; среднее арифметическое «центр набора чисел»:среднее арифметическое как некое равновесное значение, своего рода «центр масс» числового набора; среднее арифметическое достоинства и недостатки при определении среднего.
Развивающая цель: развить познавательный интерес учащихся, наблюдательность, логику, память, внимание.
Воспитательная цель: точность аккуратность математической записи.
Тип урока . Урок сообщения нового материала
Метод. Словесный, беседа, рассказ.
Литература /основная/ Автор И.Р. Высоцкий .Вероятность и статистика 7-9 класс Часть 1 Москва. «Просвещение», 2023
Ход урока
-
Организационный момент
*проверка посещаемости; *проверка готовности к уроку;
2.Мотивация учебной деятельности. Сообщение темы , цели, задачи урока
-
Сообщение нового материала.
Среднее арифметическое.
Рассмотрим таблицу. В таблице даны цены популярного смартфона в 10 разных интернет магазинах на 13 января 2022 года. Речь идёт об одном и том же смартфоне , резко выделяющихся значений нет. Найдём характерную цену смартфона в указанный день, для этого сложим все цены и поделим на число 10 по числу слагаемых.
Таблица
| Магазин | Цена | Магазин | Цена |
| 1 | 8050 | 6 | 7790 |
| 2 | 8480 | 7 | 8290 |
| 3 | 8590 | 8 | 7890 |
| 4 | 8340 | 9 | 7970 |
| 5 | 8190 | 10 | 7910 |
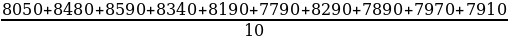 = 8150.
= 8150.
Для простоты можно считать , что массив состоит не из цены в рублях, а из чисел. Найденное значение называется средним арифметическим. На это значение можно ориентироваться при принятии решения о покупке смартфона. Цена намного выше средней, скорее всего не устроит покупателя, а цена ниже среднего значения выглядит подозрительно.
Среднее арифметическое самая употребительная – центральная мера. Поэтому среднее арифметическое значение часто называют средним значением или просто средним.
Нанесём указанные числовые значения на числовую прямую и укажем среднее значение. Выполнить самостоятельно.
Средним арифметическим числового массива называется отношение всех чисел массива к их количеству
Пять чисел меньше среднего и пять больше, причём значение 8190 довольно близко к среднему. Среднее арифметическое является центром набора чисел. Что же здесь означает слово «центр». Представим себе, что данные числа это гирьки соизмеримые с массой, в силу такого рассуждение среднее значение можно назвать центром масс. Это термин из физики и означает он точку равновесия.
Пример с гирьками характеризует главное свойство среднего арифметического, оно зависит от набора чисел и их значений. И большие и малые числа входят в среднее арифметическое с одинаковым весом. В некоторых случаях это достоинство оборачивается недостатком: если в числовой массив по случайности или в силу сложившихся обстоятельств входят значения с очень большим числом или значения с очень малым числом в таких случаях нарушается описания набора среднего значения. Данная неоднородность массива данных затруднительна ля оценки.
Среднее арифметическое хорошо описывают однородные массивы данных, то есть массивы, в которых величины имеют один и тот же смысл и нет значений которые сильно отличаются от большинства.
Закрепление:
-
Дайте определение среднего арифметического числового набора.
-
Чему равно среднее арифметическое числового набора все числа в котором равны 5,6?
-
Как можно описать среднее арифметическое с точки зрения физики?
-
Может ли среднее арифметическое числового набора быть большим чем наибольшее значение в наборе; меньшим , чем наименьшее значение?
Упражнения на закрепления:
1.Вычислите среднее арифметическое чисел:
a) 1, 2, 3, 4, 5; б) 1, 2, 3, 4, 10; в) 1, 2, 3, 4, 100; г) 1, 2, 3, 4, 1000.
2. Отметьте числа на числовой прямой. Вычислите среднее арифметическое этих чисел и отметьте его на числовой прямой:
a) 1, 2, 3, 4, 5; б) 2, 3, 4, 5, 6; в) 3, 4, 5, 6, 7; г) 10, 11, 12, 13, 14. Какую закономерность в поведении среднего значения можно заметить в каждом из случаев?
3. Можете ли вы без вычисления указать среднее значение набора чисел? Проверьте свои предположения вычислениями:
a) 13, 14, 15, 16, 17; б) 16, 17, 18, 19, 20; в) 21, 22, 23, 24, 25;
г) 20, 25, 30, 35, 40; д) 22, 24, 26, 28, 30; е) 102, 104, 106, 108, 110.
Домашнее задание: Выучить конспект урока. Уметь отвечать на вопросы. Задание из ЕГЭ решение в тетрадь с разбором.
Среднее арифметическое 6 различных натуральных чисел равно 8.
Насколько нужно увеличить наибольшее из этих чисел, чтобы их среднее арифметическое стало на 1 больше?
Решение: Имеем, среднее арифметическое равно 8, а количество чисел - 6. Получается, что 8 равно значению Х , где Х - сумма 6 различных натуральных чисел. Отсюда, сумма шести натуральных чисел равна 1 = 6 * 8 = 48. При увеличении среднего арифметического на 1, т.е. до 9 неважно, какое именно число необходимо увеличивать. Посчитаем при среднем арифметическом равным 9, чему будет сумма различных натуральных чисел 9 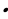 6 = 54. Значит, сумму 6 натуральных чисел (в нашем случае наибольшее) необходимо увеличить на 54 - 48 = 6, чтобы среднее арифметическое увеличилось бы на 1.
6 = 54. Значит, сумму 6 натуральных чисел (в нашем случае наибольшее) необходимо увеличить на 54 - 48 = 6, чтобы среднее арифметическое увеличилось бы на 1.
Ответ: 6







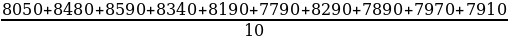 = 8150.
= 8150.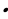 6 = 54. Значит, сумму 6 натуральных чисел (в нашем случае наибольшее) необходимо увеличить на 54 - 48 = 6, чтобы среднее арифметическое увеличилось бы на 1.
6 = 54. Значит, сумму 6 натуральных чисел (в нашем случае наибольшее) необходимо увеличить на 54 - 48 = 6, чтобы среднее арифметическое увеличилось бы на 1.



















