Геометрия 7 класс Дата : 29.11.2024
Урок № 24
Тема урока : «Свойства медианы прямоугольного треугольника,проведенной к гипотенузе»
Образовательная цель: Рассмотреть свойства медианы прямоугольного треугольника, проведенной к гипотенузе ,терему и доказательство, свойства и задачу из ОГЭ.
Развивающая цель: развивать внимание, мышление учащихся;
развивать самостоятельность учащихся, используя проблемные ситуации, творческие задания; развивать познавательный интерес к предмету.
Воспитательная цель: воспитывать чувство взаимоуважения; воспитывать у учащихся навыки учебного труда.
Тип урока: Комбинированный
Метод. Словесный, беседа, рассказ
Литература : Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
Оборудование: мел, доска, тряпка
ХОД УРОКА
Организационный момент . проверка посещаемости:
Проверка готовности к уроку.
Вступительное слово учителя. Сегодня мы узнаем, свойства медианы в прямоугольном треугольнике.
Актуализация знаний учащихся. Фронтально-индивидуальный опрос по прямоугольному треугольнику 4-5 вопросов.
Мотивация учебной деятельности. Сообщение темы,цели,задачи урока.
Формирование умений и навыков на осмысление темы урока.
Теорема
В прямоугольном треугольнике медиана, проведённая из вершины прямого угла к гипотенузе, равна половине гипотенузы.
Доказательство
Рассмотрим прямоугольный треугольник , проведём в нём из вершины прямого угла отрезок к гипотенузе, так что
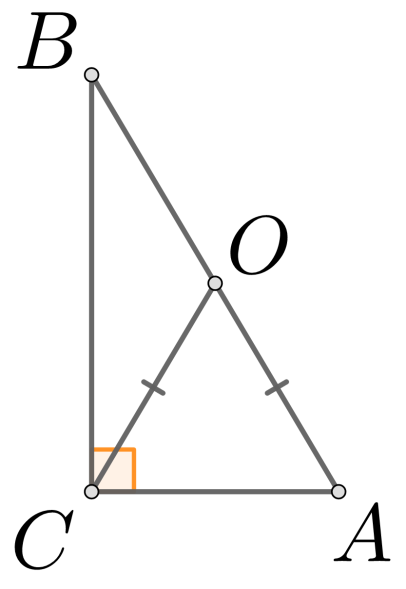
Рис. 1
Треугольник АОС— равнобедренный треугольник с основанием АС Значит, углы при основании равны: 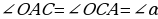 .
.
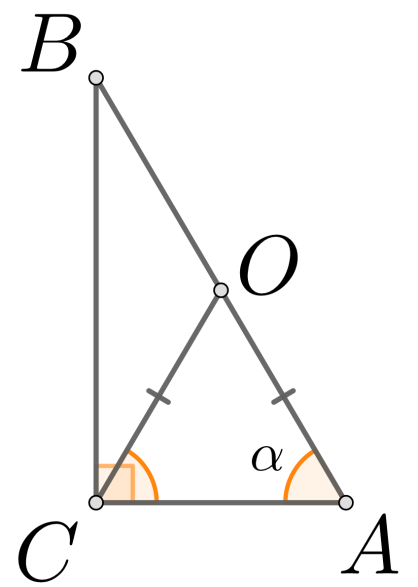
Рис. 2
Так как сумма острых углов в прямоугольном треугольнике равна 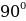 , то
, то 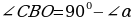
Так как угол равен 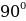 , то
, то 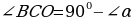 .
.
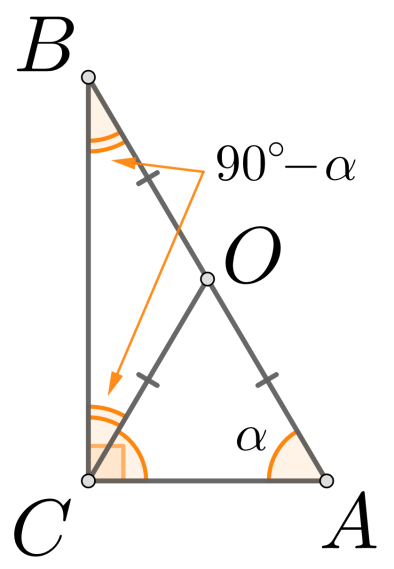
Рис. 3
Значит, 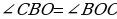 и
и 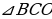 треугольник — равнобедренный. То есть стороны СО и ВО равны.
треугольник — равнобедренный. То есть стороны СО и ВО равны.
Так как СО = ОА и ВО = СО, то СО= ОА = ВО и СО = 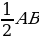 .
.
Записать свойства:
Свойства медианы в прямоугольном треугольнике
мы рассмотрим свойства медианы в прямоугольном треугольника.
Медиана — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны. Для прямоугольного треугольника это будут медианы, проведённые с острого угла к серединам катетов или с прямого к центру гипотенузы
Свойства медианы в прямоугольном треугольнике
Медианы в прямоугольном треугольнике пересекаются в одной точке, а точка пересечения делит их в соотношении два к одному считая от вершины, из которой проведена медиана.
Медиана, проведённая из вершины прямого угла к гипотенузе, равна половине гипотенузы.
Медиана, проведённая к гипотенузе прямоугольного треугольника, является радиусом описанной окружности.
Задание 6. 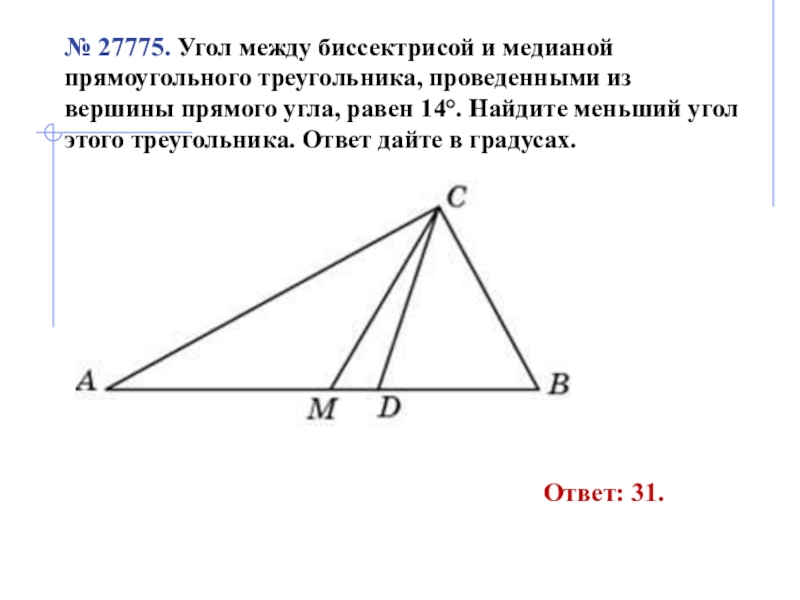
Решение.
Так как треугольник прямоугольный и медиана СМ исходит из прямого угла С, то точка М является центром описанной окружности вокруг треугольника АСВ. Следовательно, AM=MC=MB = r - радиус описанной окружности.
Найдем сначала угол МСВ. Учитывая, что СD - биссектриса, то угол DСВ равен 45°. Тогда угол МCВ равен 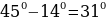 .
.
Подведение итогов урока.
Домашнее задание.








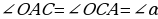 .
.
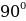 , то
, то 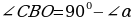
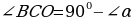 .
.
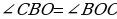 и
и 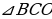 треугольник — равнобедренный. То есть стороны СО и ВО равны.
треугольник — равнобедренный. То есть стороны СО и ВО равны.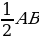 .
.
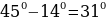 .
.

















