Россия, Новозыбков
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 24.02.2025 10:56
Ерченко Юлия Александровна
Учитель математики и информатики
34 года
2 705
22 765 
Местоположение
Специализация
Разработка урока алгебры в 9 классе на тему "Свойства элементарных функций"
Категория:
Алгебра
17.11.2019 16:41
Просмотр содержимого документа
«Разработка урока алгебры в 9 классе на тему "Свойства элементарных функций"»
Свойства элементарных функций
Цели: провести исследование элементарных функций, перечислив их основные свойства; продолжить формирование умения находить свойства функции по ее графику.
Ход урока
I. Организационный момент.
II. Актуализация ЗУН.
Вариант 1
Перечислите свойства функции, график которой изображен на рисунке.
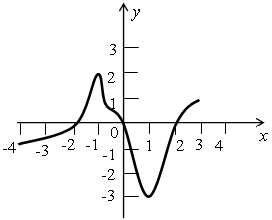
Вариант 2
Перечислите свойства функции, график которой изображен на рисунке.
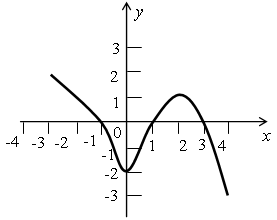
III. Объяснение нового материала.
Учащиеся уже знакомы с шестью элементарными функциями. На этом уроке они должны с высокой степенью самостоятельности описать свойства этих функций, законспектировав данный материал. При этом желательно, чтобы в их конспектах сначала были перечислены свойства функций у = х2, у = х3, у = 
и у = | х |, то есть тех функций, запись которых не содержит параметров, а затем уже исследовать функции у = kx + b и у = 
.
Справочный материал, который учащиеся изучат на этом уроке, можно составить в соответствии со следующей схемой:
1) Название функции; формула, задающая функцию.
2) Название графика функции.
3) Свойства функции.
Приведем п р и м е р н ы й к о н с п е к т материала.
| 1. Функция у = х2. График – парабола. Свойства функции: 1) D (у): (–∞; +∞); 2) Е (у): [0; +∞]; 3) у = 0, если х = 0; 4) «+»: (–∞; 0) 5) |
| |
| 2. Функция у = х3. График – кубическая парабола. Свойства функции: 1) D (у): (–∞; +∞); 2) Е (у): (–∞; +∞); 3) у = 0, если х = 0; 4) «+»: (0; +∞); «–»: (–∞; 0); 5) функция возрастающая. |
| |
| 3. Функция у = Свойства функции: 1) D (у): [0; +∞); 2) Е (у): [0; +∞); 3) у = 0, если х = 0; 4) «+»: (0; +∞); «–»: (–∞; 0); 5) функция возрастающая. |
| |
| 4. Функция у = | х |. Свойства функции: 1) D (у): (–∞; +∞); 2) Е (у): [0; +∞]; 3) у = 0, если х = 0; 4) «+»: (–∞; 0) 5) |
| |
| 5. Линейная функция у = kx + b. График – прямая. Свойства функции: 1) D (у): (–∞; +∞); 2) Е (у): (–∞; +∞), если k ≠ 0; 3) у = 0, если kx + b = 0, х = 4) у 0, если kx + b 0, y kx + b 5) при k 0 функция возрастающая, при k |
| |
| 6. Функция обратная пропорциональность График – гипербола. 1) D (у): (–∞; 0) 2) Е (у): (–∞; 0) 3) нулей нет; 4) при k 0: «+»: (0; +∞); «–»: (–∞; 0); при k «–»: (0; +∞); 5) при k при k 0 – убывающая. |
| |
(0; +∞);
: [0; +∞];
: (–∞; 0].
;
IV. Формирование умений и навыков.
Упражнения:
1. Разделите функции у = 2х + 3, у = –5х + 4, у = 
+ 1, у = 4, у = 3 – х, у = –5 + 0,7х, у = ; у = –10х на три группы:
а) возрастающие;
б) убывающие;
в) ни возрастающие, ни убывающие.
2. № 47, № 50(а).
3. При каких значениях а функция у =
а) является возрастающей;
б) является убывающей?
V. Итоги урока.
Вопросы учащимся:
– Назовите области определения и области значений всех элементарных функций.
– Есть ли среди элементарных функций те, которые не имеют нулей? имеют два нуля?
– Назовите элементарные функции, которые не принимают отрицательных значений.
– Какие из элементарных функций являются возрастающими? убывающими?
– При каких значениях k функции у = kx + b и у = являются возрастающими? убывающими?
Домашнее задание: № 44, № 45, № 46, № 50 (б).
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
