МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«Школа №19 им С.Н. Котова г. Феодосии Республики Крым»
Разработка урока
Алгебра и начала математического анализа, 10 класс
на тему: «Тригонометрические функции»
Урок разработала
Крищенко Татьяна Владимировна,
учитель математики
г.Феодосия, 2023г.
Дата: _________ Класс: 10
Урок №____
Тема: «Тригонометрические функции»
Тип урока: урок обобщающего повторения
Цель урока: Повторить, обобщить знания по теме, осуществить промежуточный контроль с проверкой на уроке.
Планируемые результаты:
Предметные:. умение решать простейшие тригонометрические уравнения; умение решать простейшие тригонометрические уравнения; диагностика усвоения системы знаний и умений учащихся
Личностные:. Проявляют устойчивый и широкий интерес к способам решения
познавательных задач, положительное отношение к урокам математики, дают оценку
результатов своей учебной деятельности.
Метапредметные:. определяют цель учебной деятельности, осуществляют поиск средств её осуществления; делают предположения об информации, которая нужна для решения учебной задачи; умеют отстаивать точку зрения, аргументируя ее, подтверждая фактами.
Оборудование: мультимедийный проектор; компьютер
Структура урока:
| 1. | Организационный момент. Постановка целей и мотивация изучения темы. |
| 2. | Формулирование темы и цели урока |
| 3. | Актуализация знаний |
| 4. | Проверка домашнего задания |
| 5. | Закрепление изученного материала |
| 6. | Физпауза |
| 7. | Самостоятельная работа |
| 8. | Итоги урока. Рефлексия. Д\З |
Ход урока:
1. Организационный момент. Постановка целей и мотивация изучения темы.
«Подобно тому как все искусства тяготеют к музыке, все науки стремятся к математике» Джордж Сантаяна (американский философ)
И сегодня мы говорим о разделе математики, который имеет огромное прикладное значение в различных областях знаний. Начнём сегодняшний урок с загадки:
- Какое слово начинается с трёх букв «Г» и заканчивается тремя буквами «Я»?
(Тригонометрия)
2. Формулирование темы и цели урока
3. Актуализация знаний
Какой раздел математики называется тригонометрией?
Тригонометрия («тригонон»- треугольник, «метрейн» - измерение) – это
раздел математики, в котором изучаются зависимости между углами и сторонами треугольников и тригонометрические функции.
Кто ввёл в употребление термин «тригонометрия»?
Термин «тригонометрия» ввёл в употребление в 1595 г. немецкий математик и богослов Варфоломей Питиск. А окончательный вид тригонометрия приобрела в XVIII веке в трудах Л.Эйлера.
Какие основные тригонометрические функции вы знаете?
Синус, косинус, тангенс и котангенс.
Что называется синусом числа t? Что называется косинусом числа t?
Синусом числа t называют ординату точки единичной окружности, которая соответствует данному числу.
Косинусом числа t называют абсциссу точки единичной окружности, которая соответствует данному числу.

Если М(t)=M(x;y), то
x=cos t
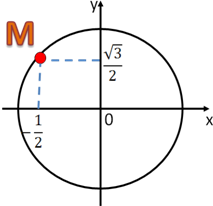 y=sin t
y=sin t
5. Назовите синус и косинус числа t, если
6. Что называется тангенсом числа t?
Что называется котангенсом числа t?
Тангенсом числа t называют отношение синуса числа t к косинусу того же числа.
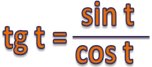
Котангенсом числа t называют отношение косинуса числа t к синусу того же числа.
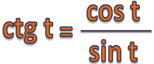
7. Сегодня мы будем вести разговор о тригонометрических уравнениях. А что называется уравнением? Какое уравнение называется тригонометрическим?
Уравнение – это равенство, содержащее переменную. А уравнения, в которых неизвестные содержатся под знаком тригонометрических функций, называются тригонометрическими уравнениями.
8. Сколько корней может иметь тригонометрическое уравнение?
Тригонометрическое уравнение либо не имеет корней, либо имеет бесконечное множество корней.
Почему?
Значения синуса и косинуса лежат в промежутке от -1 до 1. Если это условие не выполнено, то уравнение не имеет корней.
Тригонометрические функции периодические, поэтому тригонометрическое уравнение имеет бесконечное множество корней.
4. Проверка домашнего задания.
№13.27(в,г), №13.28 (в,г), 13.29 (в,г), 14.15(б), 14.22.
Задание отсканировано перед уроком, учащиеся комментируют.
5. Закрепление изученного материала
Повторим ещё раз известные нам тригонометрические формулы.
Продолжите равенство:
1-cos2t= sin(-t)=
sint= cos(-t)=
cost= tg(-t)=
1+ctg2t= ctg(-t)=
1+tg2t= sin(π+t)=
tgt= tg(2π-t)=
ctgt= ctg(π-t)=
ctgt·tgt= sin(6π+t)=
V. Закрепление изученного.
А сейчас мы продолжим решать тригонометрические уравнения.
№13.30
Решите уравнение:
а) �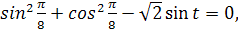 � б) �
� б) �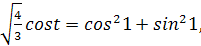 �
�
�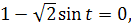 � �
� �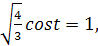 �
�
�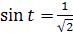 �, �
�, �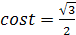 �.
�.
Ответ: �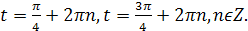 � Ответ: �
� Ответ: �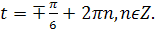 �
�
№ 13.31
а) �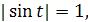 � б) �
� б) �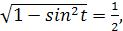 �
�
Ответ: �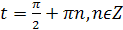 �. �
�. �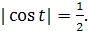 �
�
Ответ: �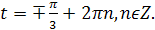 �
�
№ 14.27 (a)
Вычислите tg t, если известно, что 5 sin t – cos2t = 2,36 и �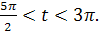 �
�
5 sin t – cos2t = 2,36,
5 sin t – 1+sin2t = 2,36,
sin2t+ 5 sin t – 3,36=0,
D=25+4∙3,36=25+13,44=38,44=6,22,
sin t =-5,6 или sin t = �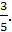 �
�
�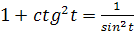 �
�
�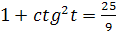 �,
�,
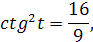
�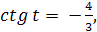 � т.к. это угол II четверти.
� т.к. это угол II четверти.
�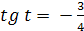 �.
�.
�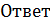 �: -0,75.
�: -0,75.
Физпауза
Не поворачивая головы, обведите взглядом стену класса по периметру по часовой стрелке, классную доску по периметру против часовой стрелки, прямоугольник, изображенный на слайде по часовой стрелке(красной) и следующий против часовой стрелки. Пробегите взглядом по жёлтой линии , затем по голубой. Поверните голову налево и посмотрите на линию горизонта, а теперь на кончик своего носа. Закройте глаза, сосчитайте до 5, откройте глаза и продолжим работу
Самостоятельная работа.
Тестовый контроль знаний.
Тест (базовый уровень)
Найдите декартовы координаты точки A�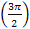 �.
�.
(-1;0); 2) (0;1); 3) (1;0); 4) (0;-1).
Вычислите: �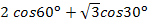 �.
�.
�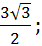 � 2) 2,5; 3) �
� 2) 2,5; 3) �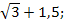 � 4) �
� 4) �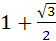 �.
�.
Упростите выражение: 5 sin2t-4+5 cos2t.
1; 2) 9; 3) -9; 4) -4.
Упростите выражение: ctg2t (cos2t-1)+1.
–sin2t; 2) cos2t; 3) sin2t; 4) -cos2t.
Сравните с нулём выражения �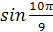 � и �
� и �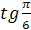 �. Выберите правильную пару ответов.
�. Выберите правильную пару ответов.
- - ; 2) - +; 3) + -; 4) + +.
На каком из рисунков изображены точки �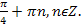 �
�
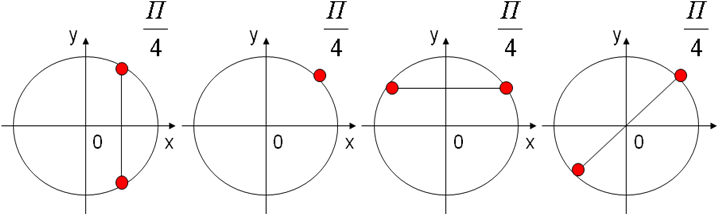
Укажите множество значений функции y=2 cos x+3.
(2;3); 2) [1;5]; 3) (1;5); 4) [2;3].
Решите уравнение: сos(-x)=1.
2πn; 2) πn; 3) �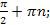 � 4) �
� 4) �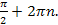 �
�
Найдите cos t , если sin t = �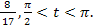 �
�
�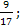 � 2) �
� 2) �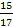 �; 3) - �
�; 3) - �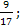 � 4) - �
� 4) - �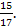 �
�
Решите уравнение: �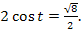 �
�
�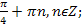 � 2) �
� 2) �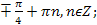 � 3) �
� 3) �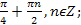 � 4) �
� 4) �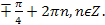 �
�
Тест (повышенный уровень).
Найдите декартовы координаты точки �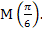 �
�
1. �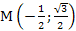 � 2. �
� 2. �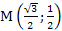 � 3. �
� 3. �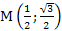 � 4. �
� 4. �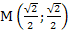 �.
�.
К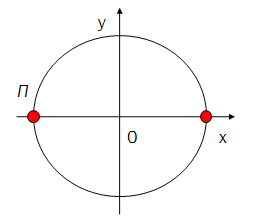 акая из формул не будет задавать все числа, которым соответствуют точки:
акая из формул не будет задавать все числа, которым соответствуют точки:
1. π+πk, kZ 2. 2πk, kZ
3. π+πk, kZ 4. πk, kZ
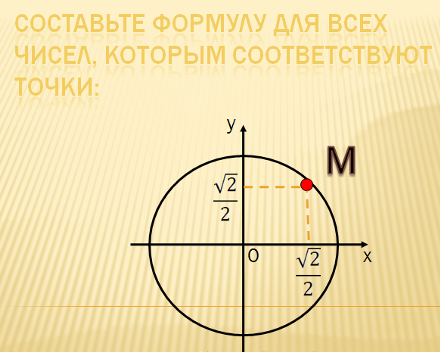
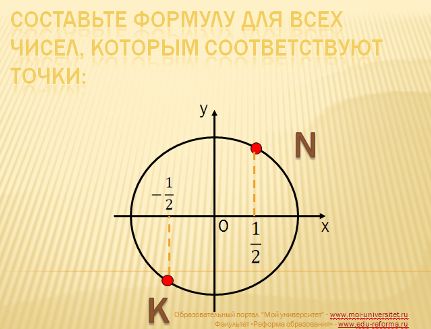
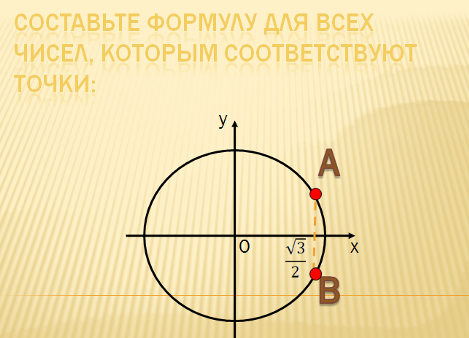
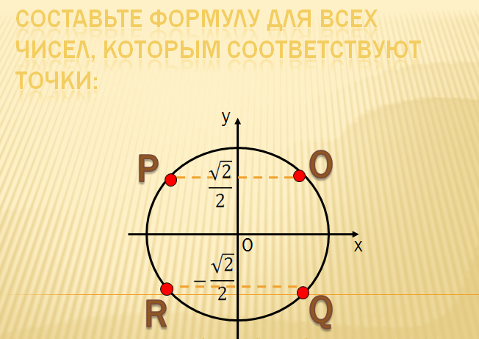
С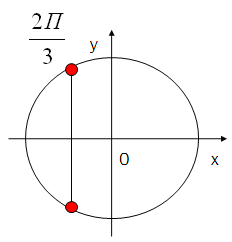 оставьте формулу для всех чисел, которым соответствуют точки:
оставьте формулу для всех чисел, которым соответствуют точки:
1. �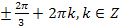 � 2. �
� 2. �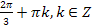 �
�
3. �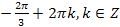 � 4. �
� 4. �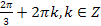 �
�
На каком из рисунков изображены точки �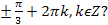 �
�
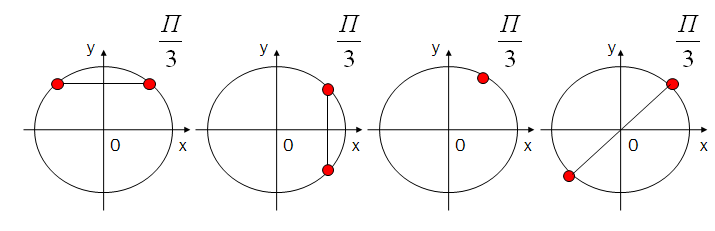
На каком из рисунков изображены точки �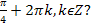 �
�
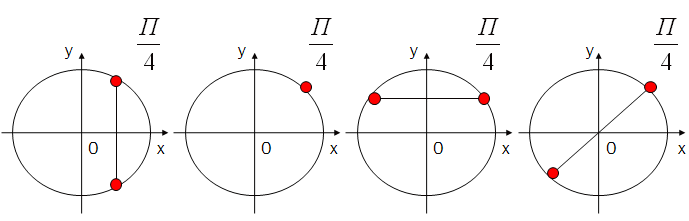
Решите уравнение �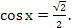 �
�
1. �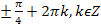 � 2. �
� 2. �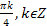 � 3. �
� 3. �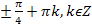 � 4. �
� 4. �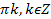 �.
�.
Решите уравнение �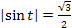 �.
�.
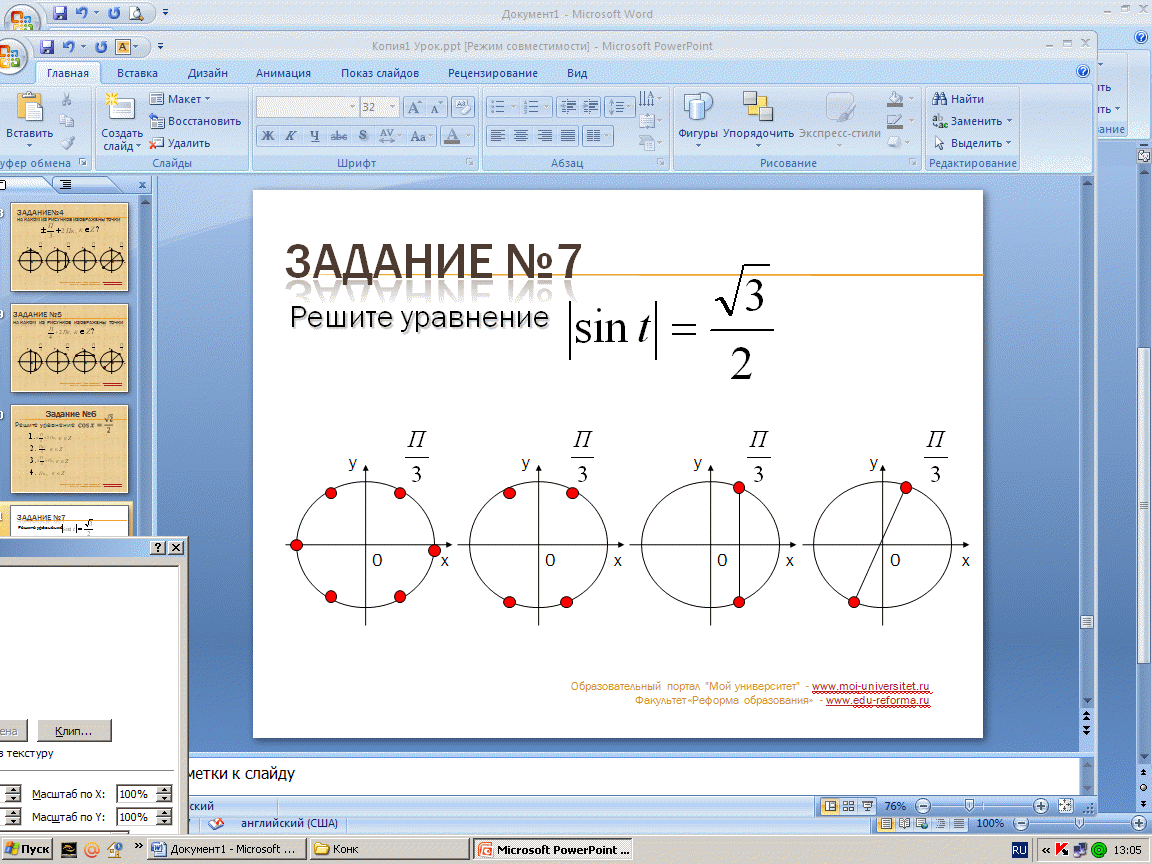
Вычислите tgt, если �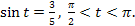 �
�
1. � � 2. �
� 2. �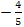 � 3. �
� 3. �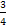 � 4. �
� 4. �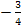 �.
�.
Упростите выражение: cos2x-1.
1. sin2x 2. -sin2x 3. �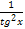 � 4. tg2x.
� 4. tg2x.
Упростите выражение: (tgt+ctgt)2.
1. �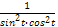 � 2. 1 3.�
� 2. 1 3.�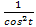 � 4. sin2t∙cos2t.
� 4. sin2t∙cos2t.
Проверка теста с необходимыми пояснениями.
Итоги урока. Рефлексия. Домашнее задание.
Выставление оценок за урок, самостоятельную работу.
Рефлексия (закончить фразу):
У меня вызвало затруднения…
У меня получается…
Мне даётся легко…
§22 № 22.1, 22.4, §14 № 14.16(а,в), №14.24









 y=sin t
y=sin t 




 акая из формул не будет задавать все числа, которым соответствуют точки:
акая из формул не будет задавать все числа, которым соответствуют точки: оставьте формулу для всех чисел, которым соответствуют точки:
оставьте формулу для всех чисел, которым соответствуют точки:












