| Основные этапы организации учебной деятельности | Деятельность учителя | Деятельность учеников | Формируемые УУД |
| I. Самоопределение Цель: - создание условий для возникновения у учеников внутренней потребности включения в учебную деятельность. | Эпиграф нашего урока: «У математиков существует свой язык - это формулы» С.В. Ковалевская (слайд1) Девиз урока: Китайская мудрость гласит, «Я слышу – я забываю, я вижу – я запоминаю, я делаю – я понимаю» (слайд2) Сегодня мы будем следовать ее указаниям. Прежде, чем приступить к работе, каждый из вас должен поставить перед собой цель сегодняшнего урока. Перед вами лежат оценочные листы
|
Настрой на сотрудничество, приветствие учителя и создание хорошего настроения.
Заполняют оценочные листы. |
Личностные: мотивация, самоопределение Регулятивные: целеполагание Коммуникативные: планирование учебного сотрудничества с учителем и одноклассниками |
| II. Актуализация знаний и фиксирование затруднений Цель: - обеспечение готовности учащихся к включению в продуктивную обучающую деятельность, повторение изученного материала. | Посмотрите на экран. Здесь написаны формулы .Здание 1. « Верно или не верно» Закончите их и сформулируйте словами. (Приложение2. Слайд3) | а2 – в2 = a2 +2ab+b2 |
| | (а + в) 2 = (а – в)(а + в) |
| | (а – в)(а + в)= а2 – в2 |
| | (а – в) 2 = a2 -2ab+b2 |
| -
Задание: «Верно или не верно»: да и нет не говорите, «+» и «-» напишите (остальные учащиеся)
| Записывают формулы, говорят название и правило, анализируют ответы, исправляют ответы одноклассников, высказывают свою точку зрения. | Личностные: смыслообразование Регулятивные: выделение и осознание того, что уже пройдено, умение выявлять предполагаемые затруднения Коммуникативные: слушать и понимать речь других |
| III. Постановка учебной задачи, целей урока.
Цель: - обсуждение затруднений, проговаривание цели урока, темы.
| Как в общем называют эти формулы? Верно. Формулы сокращенного умножения. А как мы обозначим тему нашего урока? Правильно. Применение формул сокращенного умножения. А какую цель поставим для себя на этом уроке? Правильно, закрепить умение применять формулы сокращенного умножения для преобразования целых выражений. Запишите в тетрадях число «Классная работа», тему урока.
|
Формулируют цели урока. | Личностные: задавать вопросы, необходимые для организации собственной деятельности и сотрудничества с партнёром; Регулятивные: определять и формулировать цель деятельности на уроке Познавательные: проводить сравнение, указывая на основание сравнения Коммуникативные Уметь с достаточной полнотой и точностью выражать свои мысли |
| IV. Составление плана, стратегии по разрешению затруднения и его реализация.
Цель: - обеспечение усвоения полученных знаний и способов действий на уровне применения в измененной ситуации. | Предлагает выполнить учащимся следующие задания:
ЗАДАНИЕ №2: (Приложение 2, слайд 5) Тест – соответствие. Расшифровка. Для каждого выражения из левого столбца подберите ему тождественно равное в правом: («5» - все верно, «4» - 1- 2 ошибки, «3» - 3 ошибки, «2» - более 4 ошибок)
| № формулы | формула | № ответа | ответ | буква | | 1 | (x+3)² | 1 | 4x²-9 | О | | 2 | x²-16 | 2 | 16x²-40xy+25y² | А | | 3 | (2x-3)(2x+3) | 3 | (x-4)(x+4) | И | | 4 | 81-18x+x² | 4 | (3y+6x)² | Т | | 5 | (4x-5y)² | 5 | x²+6x+9 | Д | | 6 | 25x²-49y² | 6 | (9-x)² | Ф | | 7 | 9y²+36yx+36x² | 7 | (5x-7y)(5x+7y) | Н |
Образец сверки на слайде (слайд 6) Показывает портрет великого математика Диофанта. Сообщение о Диофанте
ЗАДАНИЕ 3: ( Приложение 3,слайд 7).Замените 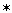 одночленом так, чтобы получившееся равенство было тождеством. Взаимопроверка. («5» - все верно, «4» - 1 ошибка, «3» - 2 ошибки, «2» - более 2 ошибок) одночленом так, чтобы получившееся равенство было тождеством. Взаимопроверка. («5» - все верно, «4» - 1 ошибка, «3» - 2 ошибки, «2» - более 2 ошибок) | 1 | 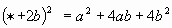
| a | | 2 | 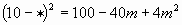
| 2m | | 3 | 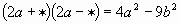
| 3b | | 4 | 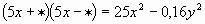
| 0,4y | | 5 | * - * =(9с – 8а)(9с + 8а) | 81c2 -64a2 | Образец сверки на слайде (слайд 8)
ЗАДАНИЕ №4: Нужно найти ошибку в каждой формуле и исправить ее. ( слайд 9). -
(4у – 3х)(4у+3х) = 8у2 – 9у2 (вместо 8у2 должно быть16у2) 2) 100х2 – 4у2 = (50х – 2у)(50х + 2у) (вместо 50х должно быть10х).
3) (3х + у)2= 9х2 – 6ху + у2 (вместо -6ху должно быть +6ху).
4) (6a – 9c)2 = 36a2 – 54ac + 81c2 (вместо -54ac должно быть -108ac).
Проверку проводим, обменявшись листиками. (слайд10)
| Каждый ученик получает карточку, выполняет задание, получает соответствия, оценивают друг друга. Один из учеников рассказывает сообщение о Диофанте: Очень давно, в Древней Греции жили и работали замечательные ученые-математики, которые всю свою жизнь отдали служению науке. В то время, все алгебраические утверждения выражали в геометрической форме. Вместо сложения чисел говорили о сложении отрезков, а произведение двух чисел сравнивали с площадью, трех чисел-с объемом и т.д. первым ученым, который отказался от геометрических способов выражения и перешел к алгебраическим уравнениям был древнегреческий ученый-математик, живший в 3 веке до нашей эры Диофант. Появились формулы, которые стали называться формулами сокращенного умножения.
Получают карточку с заданием, индивидуально выполняют его, обмениваются тетрадями, проводят взаимопроверку, оценивают друг друга
| Личностные: осуществлять взаимный контроль и оказывать в сотрудничестве необходимую взаимопомощь; Познавательные: осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий; Регулятивные: прилагать волевые усилия и преодолевать трудности и препятствия на пути достижения целей. Коммуникативные: владеть диалогической формой речи в соответствии с грамматическими и синтаксическими нормами родного языка |
| V. Этап самостоятельной работы с проверкой по эталону Цель: - умение применять правило в самостоятельной деятельности
| Предлагаю выполнить тест, который проверяет результаты выполненного задания. (Приложение № 4, слайды 11, 12,13) Этот тест проверит ваше умение применять формулы сокращенного умножения. Ваша цель-выбрать правильный ответ и записать нужную букву. При правильных ответах должно получиться слово «ВЕРНО».
| Самостоятельное решение в тетради. Осуществляют самоконтроль и взаимооценку. | Регулятивные: отличать верно выполненное задание от неверного, осуществлять констатирующий контроль по результату и по способу действия; актуальный контроль на уровне произвольного внимания; Коммуникативные: осуществлять контроль, коррекцию, оценку действий партнёра, уметь убеждать |
|
V1. Физкультминутка (микропауза для глаз)
| Крепко зажмурить глаза на 3-5 секунд, а затем открыть их на такое же время. Повторять 6-8 раз. Быстро моргать в течение 10-12 секунд, открыть глаза, отдыхать 10-12 секунд. Повторять 3 раза. Исходное положение: сидя, закрыть веки, массировать их с помощью легких круговых движений пальца. Повторять в течении 20-30 секунд. (слайд 14)
|
|
|
| VI1.Реализция выбранного проекта. | 1.Решение заданий у доски.
----------------------------- = 59²-2·59·41+41² (Слайд 15) 2.Игра “Алгебраическая мозаика”. Составить из предложенных выражений формулы.(слайд16) 3х, 5у, 3х2, 5у, 9х2, 30ху, 27х3, 125х2, 15ху, 25у2 , 125у3 . Образец сверки на слайде (слайд 17) (3x -5y)2 =9x2 -30xy + 25y2 9х2 -25у2 =(3x -5y)(3x +5y) 27x3 – 125y3 =(3x -5y)(9x2 +15xy+25y2) | Составляют формулы, обсуждают в парах. Проверяем у доски.
Применяют полученные знания. |
|
| VI11. Этап рефлексии деятельности.
Цель: - анализ и оценка успешности достижения цели; выявление качества и уровня овладения знаниями | Предлагаю дифференцированную домашнюю работу. Применив формулы сокращенного умножения, заполни таблицу: даны 5 пар выражений: на «3» 3 любых пары, «4» - 4 пары, «5» заполнена вся таблица. (Приложение № 5) Учитель предлагает оценить ученикам свою работу, подвести итоги В оценочном листе продолжить одно из предложений: “Мне понятно… “Я запомнил… “Мне на уроке… “Я думаю… Прощается с учащимися, благодарит за работу. (слайд 19) | Осознание результатов своей учебной деятельности, самооценка результатов своей работы и работы всего класса, заполнение оценочного листа, выбор домашней работы. | Личностные: Устанавливать связь между целью деятельности и ее результатом Регулятивные: осуществлять итоговый и пошаговый контроль по результату. Совместно с учителем и одноклассниками давать оценку деятельности на уроке |
| 1Х. Это интересно (при наличии времени). | -
Задумайте число (до 10); -
Умножьте его на себя; -
Прибавьте к результату задуманное число; -
К полученной сумме прибавьте 1; -
К полученному числу прибавьте задуманное число. Решение: x² + x + 1 + x = x² + 2x + 1 = (x + 1)² Например: 5·5 + 5 + 1 + 5 = 36, тогда x = √36 – 1 = 6 – 1 = 5.
-
2). 15² = 1 ∙ 2 + 25 = 225; -
25² = 2 ∙ 3 + 25 = 625; -
55² = 5 ∙ 6 + 25 = 3025; -
65² = 6 ∙ 7 + 25 = 4225; -
95² = 9 ∙ 10 + 25 = 9025; -
105² = 10 ∙ 11 + 25 = 11025.
|
|
|







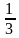 b
b


















