Тема: Умножение и деление натуральных чисел.
Планируемые результаты:
в направлении личностного развития
- развитие логического и критического мышления, культуры речи;
- формирование у учащихся интеллектуальной честности и объективности;
- воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;
- развитие интереса к математике, математических способностей;
2) в предметном направлении
- умение работать с математическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно излагать свои мысли в устной и письменной речи;
- овладение навыками устных и письменных вычислений;
- овладение приемами решения уравнений, умение применять аппарат уравнений для решения задач;
3) в метапредметном направлении
- первоначальные представления о математике как об универсальном языке науки и техники;
- умение видеть математическую задачу в окружающей жизни;
Ход урока.
1. Организационный момент.
Здравствуйте ребята! Я пришла к вам на урок вот с таким настроением (показываю 5 на руке)! А какое у вас настроение?
Улыбнитесь друг другу и пожелайте хорошего настроения! «А начну я урок с такой притчи:
Однажды к отцу подошел сын, он что-то нежно держал в закрытых ладонях. Сын спросил: “Папа, какая у меня в руках бабочка: живая или мертвая?”. Папа не стал разглядывать руки мальчика, а просто сказал ему: “Все в твоих руках”. Сын сначала не понял, но через некоторое время ему стал ясен смысл притчи. Вот и наш сегодняшний урок в наших руках. Либо знания упадут мертвым грузом, либо они позволят вам взлететь ввысь. Как вы думаете, какой из этих вариантов является целью нашей работы?
Кто согласен?
Я рада, что мы все настроены на единую цель.»
Работать нам придется много и я думаю не зря. А оценивать свою работу вы будете на листе самооценки.
Лист самооценки!!!
2. Актуализация знаний. А вот изучение математики нам будет очень трудно осваивать без умения быстро и верно считать, поэтому начнем урок с проверки теоретических знаний.
Графический диктант "Верно ли?"
1. Числа, которые перемножают, называют множителями. (ДА).
2. В выражении (175-100):25 скобки можно не писать, т.к. при этом порядок действий не изменится. (НЕТ).
3. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель. (ДА)
4. При умножении числа на единицу получиться то же самое число. (ДА)
5. Числа, которые делят, называют множителями. (НЕТ).
6. Результат деления называют частным. (ДА).
7. Чтобы найти неизвестный делитель, нужно частное разделить на делимое. (НЕТ).
8. Чтобы найти неизвестное делимое, нужно частное умножить на делитель. (ДА).
9. При делении числа на нуль в результате получиться нуль. (НЕТ),
10. Если среди множителей есть нуль, то произведение равно нулю. (ДА),
11. Чтобы найти во сколько раз одно число больше другого, нужно выполнить вычитание. (НЕТ).
Во время графического диктанта работают по карточкам на боковых досках:
1 карточка
Теоретическая часть
1. Как называют числа, которые перемножают?
2. Чему равно 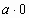 ?
? 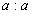 ?
?
3. Как найти неизвестный делитель?
4. Вычислить: 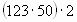
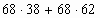 . Обьясни какие законы умножения применил.
. Обьясни какие законы умножения применил.
5. Решите уравнение: 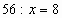
Ответы. №1. Множители № 2. 0;1 № 3. Чтобы найти неизвестный делитель, нужно делимое разделить на частное. №4. Чтобы умножить произведение двух чисел на третье число можно умножить первое число на произведение второго и третьего чисел. № 5. 7
2 карточка
Теоретическая часть
1. Как найти неизвестный множитель?
2. Чему равно 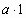 ?
? 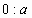 ?
?
3. Как найти неизвестное делимое?
4. Вычислить: 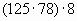
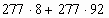 . Обьясни какие законы умножения применил.
. Обьясни какие законы умножения применил.
5. Решите уравнение: 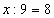
Ответы. №1. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель №2. 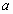 ;0 №3. От перестановки множителей значение произведения не меняется. № 4. Чтобы найти неизвестное делимое, нужно частное умножить на делитель. №5. 72
;0 №3. От перестановки множителей значение произведения не меняется. № 4. Чтобы найти неизвестное делимое, нужно частное умножить на делитель. №5. 72
3 карточка
1.Вместо квадратиков запишите такие числа, не равные нулю, чтобы значение полученных выражений было легко вычислить устно:
а) 2 ∙ 78 ∙ = ?
б) 3 · · 7 ∙ 25 = ?
в) · 9 ∙ 125 = ?
4 карточка
1. Ученик записал выражение: 25 ∙ Х ∙ 4. потом он вместо Х стал подставлять в это выражение по очереди числа: 13; 21; 39; 47. найдя значения каждого произведения, он очень удивился тому, что все числа оказались круглыми.
Не могли бы вы объяснить, почему?
Сколько будет стоять в конце каждого числа нулей?
2) Угадайте корни уравнения:
а) х + х = 64 б) 58 + у + у + у = 58.
Молодцы, хорошо справились. Не забудьте оценить свою работу в листах самооценки.
Если вы правильно посчитаете мною предложенные примеры, вы узнаете тему урока.
Выполните действия:
1) 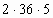 Н
Н
2) 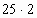 И
И
3)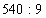 М
М
4)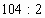 У
У
5) 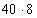 О
О
6) 100:4 Ж
7) 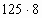 Е
Е
8)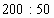 Д
Д
9) 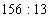 Л
Л
10) 400:0 К
| 52 | 60 | 360 | 320 | 25 | 1000 | 360 | 50 | 1000 |
| у | м | н | о | ж | е | н | и | е |
и
| 4 | 1000 | 12 | 1000 | 360 | 50 | 1000 |
| д | е | л | е | н | и | е |
3. Целепологание и мотивация. Итак, как звучит наша тема? Умножение и деление натуральных чисел, и их свойства.
Учитель: Ребята, но разве мы с вами не достаточно хорошо знакомы с этими действиями? Но, мне хочется доказать и показать вам насколько интересна и увлекательна может быть математика.
Кто из вас не любит сказки? А 1000 и 1 ночь Шахерезады. Слышали про такую сказку?
А знаете ли вы, что число 1001 называют числом Шахерезады? А что же такого сказочного и загадочного в этом числе? Оказывается, любое трехзначное число можно легко умножить на 1001, в результате получим число состоящее из двух данных трехзначных числе. Например: 654*1001=654654. Здорово правда?
Но таких загадок в математике очень много и сегодня я хотела бы познакомить вас только с некоторыми из них. А мы уже с вами знакомы с одной такой загадкой? (умножение на 11)
Приемы быстрого умножения.
С древних времен практиковались многочисленные и разнообразные правила умножения и деления.
Я попросила Влада подготовить рассказать еще об одном приеме быстрого счета.
В одной старинной русской рукописи описывается интересный прием «умножения крестиком», применявшийся еще в Древней Индии под названием «молниеносного».
Пусть требуется , например, умножить 48 на 27.
Пишем 48
27
Говорим: 7*8=56;
Пишем : 6, в уме 5 48
27
6
Говорим: 7*4=28; 28+5=33;
33 в уме, 2*8=16;
16+33=49;
Пишем 9, в уме 4; 48
27
9 6
Говорим: 2*4=8; 8+4=12;
Пишем 12 и получаем произведение 1296
48
27
129 6.
Этим способом удобно пользоваться и в настоящее время.
Этап решения с проговариванием во внешней речи.
Давайте попробуем вместе с вами на доске решить пример: 34*26=884
(Влад рядом стоит контролирует)
Русский способ умножения.
Этот прием умножения использовался русскими крестьянами примерно 2-4 века назад, а разработан был еще в глубокой древности. Суть этого способа та:“На сколько мы делим первый множитель, на столько умножаем второй”.Вот пример: Нам нужно 32 умножить на 13. Вот как бы решили этот пример 3-4 века назад наши предки:
32 * 13 (32 делим на 2, а 13 умножаем на 2)
16 * 26 (16 делим на 2, а 26 умножаем на 2)
8 * 52 (и т.д.)
4 * 104
2 * 208
1 * 416 =416
Деление пополам продолжают до тех пор, пока в частном не получится 1, параллельно удваивая другое число. Последнее удвоенное число и дает искомый результат. Нетрудно понять, на чем этот способ основан: произведение не изменяется, если один множитель уменьшить вдвое, а другой вдвое же увеличить. Ясно поэтому, что в результате многократного повторения этой операции получается искомое произведение
Однако как поступить, если при этом приходится делить пополам число нечетное? Народный способ легко выходит из этого затруднения. Надо, - гласит правило, - в случае нечётного числа откинуть единицу и делить остаток пополам; но зато к последнему числу правого столбца нужно будет прибавить все те числа этого столбца, которые стоят против нечетных чисел левого столбца: сумма и будет искомым произведением. Практически это делают так, что все строки с четными левыми числами зачеркивают; остаются только те, которые содержат налево нечетное число. Приведем пример (звездочки указывают, что данную строку надо зачеркнуть):
19*17
9*34
4 *68*
2 *136*
1 *272
Сложив незачеркнутые числа, получаем вполне правильный результат:
Ответ: 323.
|  97 97
| 19 |
| 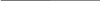 48 48
| 38 |
|  24 24
| 76 |
|  12 12
| 152 |
|  6 6
| 304 |
| 3 | 608 |
| 1 | 1216 |
Закрепление с проговариванием во внешней речи.
1 ученик на доске 48*27.
Рассматриваем приемы умножения на 5,50.
1 ученик на доске.
846*5, 124*50.
А знаете как легко перемножить числа, заключенные между 10 и 20?
Об этом вам расскажет Сычева Анастасия.
Допустим, нам нужно умножить 17 на 14. К сумме одного из сомножителей с единицами другого, умноженной на 10, прибавляем произведение единиц.
17*14= (17+4) *10 + 7*4= 210=28=238.
Попробуйте сами: 16*14.
Этап закрепления с проговариванием во внешней речи.
Умножение на 9, 99, 999, 9999, 99999 Учащимся предлагается (в виде соревнования) выполнить умножение различными способами: Умножение столбиком 786 • 9 = 786(10 - 1) = 786 • 10 – 786 = 7860 – 786 = 7074 (для умножения многозначного числа на 9 надо приписать к нему справа нуль и вычесть из результата множимое число). При умножении на 99, приписывают два нуля, на 999, приписывают три нуля и т.д. 456 • 99 = 45600 – 456 = 45144 598 • 999 = 598000 – 598 = 597402
А можно ли применить этот способ если умножать на 9999? А я могу это сделать устно:
Ребята, я на доске сейчас запишу четырехзначное число состоящие из девяток 9999, один из вас на доске запишет любое тоже четырехзначное число. Каждый из вас перемножит эти числа (время засекается). Учитель в это время быстро записывает ответ на листе бумаги или на доске. После выполнения умножения ответы сверяют… у ребят – восторг! Они просят еще задание. Можно дать теперь пятизначное число 99999. 99999 • 74586 = 7458525414 999999 • 683498 = 683497316502 В результате умножения, получается десятизначное число: первые пять цифр его есть умножаемое число, только уменьшенное на единицу, а остальные пять цифр «дополнения, первой пятерки.
Этап самостоятельной работы с взаимопроверкой.
| 1 вариант
| 2 вариант
|
| 476*5=2380
| 832*5=4160 |
| 658*5=3290
| 756*50=37800 |
| 56*9=504 | 61*9=549 |
| 723*99=71577 | 785*99=77715 |
| 16*13=208 | 18*15=270 |
| 346*1001=346346 | 875*1001=875875 |
Рефлексия:
| 225 | 204 | 2585 | 204 | 162 | 1200 | 4000 | 32706729 |
| м | 0 | л | о | д | ц | ы | ! |
18*9=162 (д)
235*11=2585 (л)
9999*3271=32706729 (!)
12*17=204 (о)
240*5=1200 (ц)
15*15=225 (м)
160*25=2000 (ы)
Однажды странники устраивались на ночлег на усыпанном галькой морском берегу. Вдруг с небес ударил столб света. Странники смекнули, что услышат божественное откровение, и приготовились ждать. Через некоторое время с небес раздался голос. Голос сказал: "Наберите гальки и положите в сумки. Наутро отправляйтесь в путь. Идите весь день. Вечером вы будете радоваться и грустить одновременно". После этого и свет, и голос исчезли. Странники были разочарованы. Они ждали важного откровения, вселенской правды, которая сделала бы их богатыми и знаменитыми, а вместо этого получили задание, смысла которого не понимали. Однако, вспоминая о небесном сиянии, они на всякий случай с ворчанием побросали в сумки несколько мелких камешков. Странники провели в пути весь следующий день. Вечером, укладываясь спать, они заглянули в свои сумки. Вместо гальки в них лежали алмазы. Сначала странников охватила радость: они обладатели алмазов! А через мгновение - грусть: алмазов было так мало! Мораль: я очень надеюсь на то, что знания приобретенные сегодня на уроке, истинную ценность которых возможно вы сегодня и не поняли, в дальнейшем обратятся в «алмазы»).
Задание на дом: продолжить работу над проектом.
1 карточка
1. Как называют числа, которые перемножают?
2. Чему равно 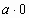 ?
? 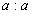 ?
?
3. Как найти неизвестный делитель?
4. Вычислить: 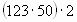
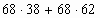 . Обьясни какие законы умножения применил.
. Обьясни какие законы умножения применил.
5. Решите уравнение: 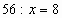
2 карточка
1. Как найти неизвестный множитель?
2. Чему равно 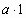 ?
? 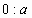 ?
?
3. Как найти неизвестное делимое?
4. Вычислить: 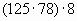
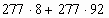 . Обьясни какие законы умножения применил.
. Обьясни какие законы умножения применил.
5. Решите уравнение: 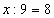
3 карточка
1.Вместо квадратиков запишите такие числа, не равные нулю, чтобы значение полученных выражений было легко вычислить устно:
а) 2 ∙ 78 ∙ = ?
б) 3 · · 7 ∙ 25 = ?
в) · 9 ∙ 125 = ?
4 карточка
1. Ученик записал выражение: 25 ∙ Х ∙ 4. потом он вместо Х стал подставлять в это выражение по очереди числа: 13; 21; 39; 47. найдя значения каждого произведения, он очень удивился тому, что все числа оказались круглыми.
Не могли бы вы объяснить, почему?
2) Угадайте корни уравнения:
а) х + х = 64 б) 58 + у + у + у = 58.
| 1 вариант
| 2 вариант
|
| 476*5=
| 832*5 |
| 658*5
| 756*50 |
| 56*9 | 61*9 |
| 723*99 | 785*99 |
| 16*13 | 18*15 |
| 346*1001 | 875*1001 |
| 1 вариант
| 2 вариант
|
| 476*5=
| 832*5 |
| 658*5
| 756*50 |
| 56*9 | 61*9 |
| 723*99 | 785*99 |
| 16*13 | 18*15 |
| 346*1001 | 875*1001 |
| 1 вариант
| 2 вариант
|
| 476*5=
| 832*5 |
| 658*5
| 756*50 |
| 56*9 | 61*9 |
| 723*99 | 785*99 |
| 16*13 | 18*15 |
| 346*1001 | 875*1001 |
| 1 вариант
| 2 вариант
|
| 476*5=
| 832*5 |
| 658*5
| 756*50 |
| 56*9 | 61*9 |
| 723*99 | 785*99 |
| 16*13 | 18*15 |
| 346*1001 | 875*1001 |






 97
97 48
48









