Просмотр содержимого документа
«Разработка урока "Производная и ее геометрический смысл"»
РАЗРАБОТКА УРОКА
Обобщение и систематизация знаний по теме
«Производная и ее геометрический смысл»
Цель урока:
Проконтролировать знаний правил дифференцирования, основных формул для нахождения производных функции, уравнения касательной к графику функции.
Проверить навыки по применению знаний в решении нестандартных задач, развить представление учащихся об использовании знаний по нахождению производной в окружающей их жизни и в других научных областях, продолжить формировать умения работать самостоятельно, воспитывать волю и настойчивость для достижения результатов.
Тип урока:
Урок обобщения и систематизации знаний.
Оборудование: проектор, карточки.
ХОД УРОКА
Организационный момент
Эпиграф урока
«Был этот мир глубокой тьмой окутан
Да будет свет! И вот явился Ньютон».
Догадались почему?
Давайте сделаем экскурсию в историю. (Ученик делает небольшую историческую справку).
Откройте тетради и запишите тему урока. Проверим домашнее задание (ответы). Для того, чтобы включиться в работу и сконцентрироваться, предлагаю вам небольшую теоретическую разминку.
Актуализация знаний
Вопросы
Сформулируйте определение производной функции в точке.
Сформулируйте правила дифференцирования суммы, произведения, частного.
Назовите производные элементарных функций
В чем заключается механический смысл производной?
В чем заключается геометрический смысл производной?
Назовите уравнение касательной к графику функции в заданной точке
Решение задач
Найти производные функции
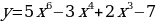
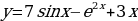
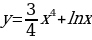
Четверо учащихся работают по карточкам. У доски решает ученик.
1.Напишите уравнение касательной к графику функции 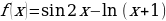 в точке с абсциссой х0=0.
в точке с абсциссой х0=0.
2.Решить уравнение
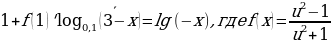 . Ответ 2.
. Ответ 2.
Вы часто спрашиваете «А зачем изучать ту или иную тему? В данном случае «Производную»?
Историческая справка «Задача Дидоны».
Применение производной. (Слайды).
Ученик решает задачу. При каком значении а касательная к параболе 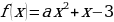 в точке М(1; а-2) параллельна прямой 3у-6х=1.
в точке М(1; а-2) параллельна прямой 3у-6х=1.
(Ответ а=0,5).
Самостоятельная работа
| 1 вариант 1.Точка движется прямолинейно по закону 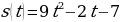 (время измеряется в секундах, путь в метрах). В какой момент времени (в секундах) скорость точки будет равняться 70м/с? (время измеряется в секундах, путь в метрах). В какой момент времени (в секундах) скорость точки будет равняться 70м/с? 2.Вычислить: 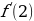 , если , если 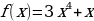
| 2 вариант Точка движется прямолинейно по закону 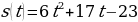 (время измеряется в секундах, путь в метрах). В какой момент времени (в секундах) скорость точки будет равняться 125м/с? (время измеряется в секундах, путь в метрах). В какой момент времени (в секундах) скорость точки будет равняться 125м/с? 2.Вычислить: 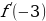 , если , если 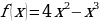
|
Домашнее задание
Повторить п. 44 – 48
Выполнить стр. 258 «Проверь себя» - №2, 3,4.
Итог урока
Сегодня каждый из Вас оценил свои знания по данной теме и может еще подкорректировать их, готовясь к контрольной работе. (Объявить оценки)
Рефлексия
Музыка может возвышать или умиротворять душу, Живопись – развивать глаз, Поэзия – пробуждать чувства, Философия – удовлетворять потребность раз ума, Инженерное дело – совершенствовать материальную сторону жизни людей, а Математика, способна достичь всех этих целей.






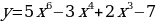
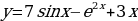
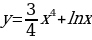
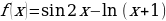 в точке с абсциссой х0=0.
в точке с абсциссой х0=0.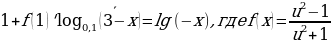 . Ответ 2.
. Ответ 2.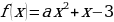 в точке М(1; а-2) параллельна прямой 3у-6х=1.
в точке М(1; а-2) параллельна прямой 3у-6х=1. 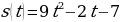 (время измеряется в секундах, путь в метрах). В какой момент времени (в секундах) скорость точки будет равняться 70м/с?
(время измеряется в секундах, путь в метрах). В какой момент времени (в секундах) скорость точки будет равняться 70м/с?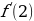 , если
, если 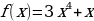
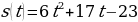 (время измеряется в секундах, путь в метрах). В какой момент времени (в секундах) скорость точки будет равняться 125м/с?
(время измеряется в секундах, путь в метрах). В какой момент времени (в секундах) скорость точки будет равняться 125м/с?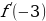 , если
, если