9 Алгебра
28.11.2022
Конспект урока
Тема: Целое уравнение и его корни.
Цели урока: ввести понятие целого уравнения и его степени; умение определять степень целого уравнения; познакомить со способами решения целых уравнений.
Ход урока
I. Организационный момент:
- Начать этот урок я хочу с притчи:
«Однажды к учителю подошел ученик, который поймал бабочку и спросил: «Учитель, какая у меня в руках бабочка: живая или мертвая?»
Учитель, даже не взглянув на ученика ответил: «Все в твоих руках»».
- Вот и наш сегодняшний урок в наших руках.
II. Актуализация знаний.
а) х2 = 0;
б) 3х + 1 = 5 + 3х;
в) х2 – 5 = 0;
г) х2 = 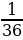 ;
;
д) х2 = 25;
е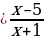 = 0.
= 0.
- Ребята что вы видите на картинке? (Уравнения)
- Что такое уравнение? (Равенство содержащее переменную)
- А что с уравнением обычно делают? (Решают)
- А что значит решить уравнение? (Найти все его корни, или доказать, что корней нет).
- Что называется корнем уравнения? (Значение переменной, при котором уравнение обращается в верное числовое равенство).
- Молодцы! Ребята, посмотрите, пожалуйста, еще раз внимательно на экран! Данные уравнения отличаются друг от друга? (Да, здесь целые уравнения и дробные рациональные)
-Назовите под какими буквами целые уравнения, и под какими дробно- рациональные. (а,б,в,г,д- целые; е- дробное рациональное).
-Итак, тема нашего урока «Целое уравнение и его корни».
III. Изучение нового материала.
Определение: Целым уравнением с одной переменной называется уравнение, левая и правая части которого - целые выражения.
Отличие целого уравнения от дробного рационального заключается в том, что областью определения целого уравнения является множество всех действительных чисел. То есть аргумент может принимать любые значения.
Среди уравнений найдем те, которые являются целыми уравнениями с одной переменной.
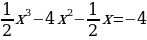
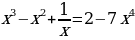
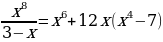
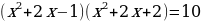
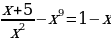
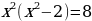
Целыми будут следующие уравнения.
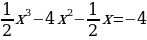
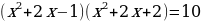
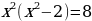
Каждое из этих уравнений можно преобразовать.
Выполним преобразования в первом уравнении:
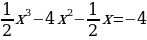
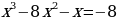
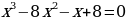
Во втором уравнении:
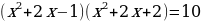
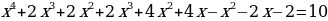
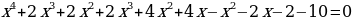
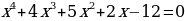
В третьем уравнении:
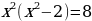
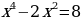
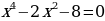
В каждом из рассмотренных примеров мы выполняли такие преобразования, которые приводят к уравнению, равносильному данному. В результате получали уравнение, имеющее вид Р(х)=0, где Р(х) – многочлен стандартного вида.
Вообще, всякое целое уравнение можно заменить равносильным ему уравнением, левая часть которого – многочлен стандартного вида, а правая – нуль.

Определение: Степень многочлена P(x) называют степенью уравнения P(x)=0.
Рассмотрим примеры: определить степень уравнений.
1. х8 + 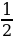
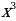 + 5 = 0; Ответ: 8
+ 5 = 0; Ответ: 8
2. 0,3х7 + 1 = 0 Ответ: 7
3. х5 + х8 (х3–2) = 0
х5 + х11 – 2х8=0
х11 – 2х8 + х5 = 0; Ответ: 11
4. (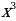 – 2)(
– 2)(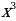 + 2) =0
+ 2) =0
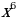 – 4 = 0 Ответ: 6
– 4 = 0 Ответ: 6
Любое уравнение 1 - й степени можно привести к виду:
ах + b = 0 - это линейное уравнение, и оно имеет не более одного корня.
Уравнение 2 - й степени можно привести к виду:
a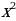 + bx + c = 0 - это квадратное уравнение и оно имеет не более двух корней.
+ bx + c = 0 - это квадратное уравнение и оно имеет не более двух корней.
Уравнение 3 - й степени можно записать в виде a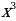 + b
+ b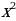 + cx + d = 0, оно имеет не более трёх корней.
+ cx + d = 0, оно имеет не более трёх корней.
Уравнения 4-й степени можно представить в виде:
a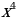 +b
+b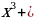 c
c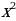 +dx+e=0 , оно имеет не более четырёх корней.
+dx+e=0 , оно имеет не более четырёх корней.
Любое целое уравнение n - й степени можно представить в таком виде 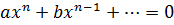 , оно имеет не более n корней.
, оно имеет не более n корней.
Причём, во всех этих случаях, a≠0.
IV. Формирование умений и навыков.
Рассмотрим некоторые методы решения целых уравнений.
Пример №1.
Решить уравнение:
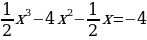 (умножим обе части уравнения на 2)
(умножим обе части уравнения на 2)
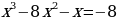
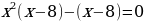
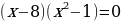
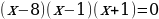
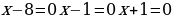
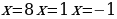
Данное уравнение имеет три корня.
Ответ: х = –1, х = 1, х = 8
Пример №2.
Решить уравнение.
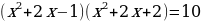
Так как для него трудно найти способ решения, будем работать с исходной записью. Введём замену:
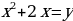
Получим новое уравнение, решим его:
(у - 1) (у +2) = 10
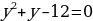
D = 49 0, два корня
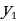 = – 4
= – 4
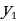 = 3
= 3
Выполним обратную замену:
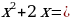 – 4 или
– 4 или 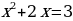
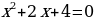 4 или
4 или 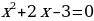
D = –12 D = 16 0,
нет корней два корня: 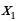 = –3;
= –3; 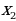 = 1.
= 1.
Ответ: х = –3; х = 1
При решении этого уравнения мы применили способ введения новой переменной. С помощью этого способа легко решать уравнения вида 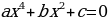
Алгоритм решения биквадратного уравнения:
1. Ввести новую переменную 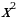 = y.
= y.
2. Решить уравнение 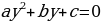 , полученное после подстановки новой переменной.
, полученное после подстановки новой переменной.
3. Выполнить обратную подстановку y = 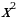 .
.
4. Найти корни исходного биквадратного уравнения.
Пример №3
Решить уравнение:
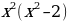 =8
=8
Приведем его к биквадратному уравнению:
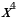 – 2
– 2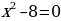
Введём новую переменную и выполним подстановку:
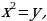
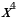 =
= 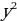
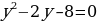
D = 36 0, два корня
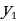 = 4
= 4
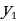 = –2
= –2
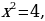 х = ±2
х = ±2
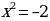 , нет корней
, нет корней
Ответ: х = ±2
Пример №4.
Решить уравнение № 276 (а, в).
Р е ш е н и е
а) (2х2 + 3)2 – 12 (2х2 + 3) + 11 = 0.
З а м е н а: 2х2 + 3 = y;
y2 – 12e + 11 = 0;
y1 = 1 y2 = 11.
В е р н е м с я к з а м е н е:
| 2х2 + 3 = 1; или 2х2 = –2. Решений нет. | 2х2 + 3 = 11; 2х2 = 8; х2 = 4; х = ± 2. Ответ: ± 2
|
в) (х2 + х – 1) (х2 + х + 2) = 40.
З а м е н а: х2 + х – 1 = y;
y (y + 3) = 40;
y2 + 3y – 40 = 0;
y1 = –8, y2 = 5.
В е р н е м с я к з а м е н е:
| х2 + х – 1 = –8; или х2 + х + 7 = 0; D = 1 – 28 = –27. Решений нет. | х2 + х – 1 = 5; х2 + х – 6 = 0; х1 = –3, х2 = 2.
|
Ответ: –3; 2.
V. Итоги урока.
Вопросы учащимся:
– Какое уравнение называется целым?
– Что такое степень целого уравнения?
– Какова степень уравнения 2х3 – 5 + х6 = 0?
– Сколько корней может иметь целое уравнение первой степени? второй степени?
Домашнее задание:
§5, стр. 75-78 читать, выучить определения и алгоритм.
Выполнить № 265, 267 (а, б), 277 (а), 278 (а)







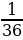 ;
; 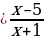 = 0.
= 0.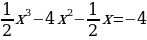
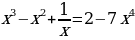
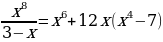
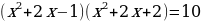
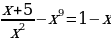
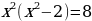
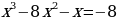
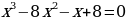
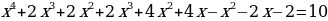
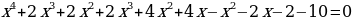
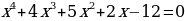
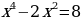
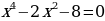

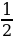
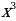 + 5 = 0; Ответ: 8
+ 5 = 0; Ответ: 8 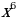 – 4 = 0 Ответ: 6
– 4 = 0 Ответ: 6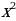 + bx + c = 0 - это квадратное уравнение и оно имеет не более двух корней.
+ bx + c = 0 - это квадратное уравнение и оно имеет не более двух корней.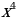 +b
+b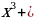 c
c
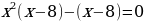
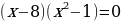
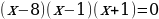
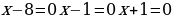
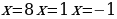
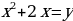
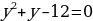
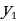 = – 4
= – 4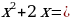 – 4 или
– 4 или 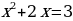
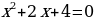 4 или
4 или 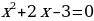
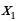 = –3;
= –3; 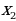 = 1.
= 1. 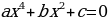

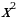 = y.
= y.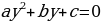 , полученное после подстановки новой переменной.
, полученное после подстановки новой переменной.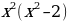 =8
=8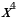 – 2
– 2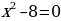
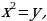
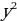
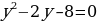
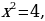 х = ±2
х = ±2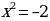 , нет корней
, нет корней









