Школа: МОУ «Лицей №1» г. Воркуты.
Учитель: Курылева Светлана Сергеевна
Предмет: Геометрия
Класс: 8 (с углубленным изучением математики).
Тема: Описанные четырехугольники (четвертый урок по теме «Вписанная и описанная окружности»)
Тип урока: урок обучения умениям и навыкам.
Форма урока: комбинированный урок.
Формы работы, используемые на уроке: фронтальная, групповая, индивидуальная.
Методы и приемы, используемые на уроке: словестные, наглядные, поисковые; учет возрастных особенностей, создание ситуации успеха, выбор действия в соответствии с возможностями ученика.
Цели на урок: ввести понятие описанного многоугольника, ознакомить учащихся со свойствами описанного четырехугольника.
Задачи на урок:
-
дидактические: изучить определение описанного четырёхугольника, доказать теорему о свойстве сторон описанного четырёхугольника, познакомить с двойственностью свойств сумм противоположных сторон и противоположных углов вписанного и описанного четырёхугольников, дать опыт практического применения рассмотренных теорем при решении задач, провести первичный контроль уровня усвоения нового материала.
-
развивающие: развивать познавательный интерес у учащихся, логическое мышление, интеллектуальные способности; формировать математическую речь; развивать умения применять знания в конкретной ситуации; развитие самостоятельной деятельности обучающихся.
-
воспитательные: воспитывать у учащихся потребность в приобретении и углублении знаний, вырабатывать умение слушать и вести диалог, формировать эстетические навыки при оформлении записей в тетради.
Оборудование: компьютеры, мультимедийный проектор, экран, листы на каждого ученика с подбором заданий по теме урока, заданий для индивидуальной работы, таблица «Примеры описанных четырехугольников», компьютерный тест по теме «Вписанные и описанные многоугольники».
Средства обучения: мультимедийная презентация к уроку «Описанные четырехугольники».
Программные средства: Microsoft Word, Microsoft Power Point.
План урока:
-
Организационный момент. (2 мин.)
-
Актуализация знаний. (8 мин.)
-
Изучение нового материала. (11 мин.)
-
Решение задач. (20 мин.)
-
Домашнее задание.(1 мин.)
-
Рефлексия. Итоги урока. (3 мин.)
План – конспект урока по теме «Вписанная окружность»
I.Организационный момент
Проверка готовности учащихся, сообщение темы и цели урока, постановка задач.
II.Актуализация знаний.
-
Математический диктант.
-
Можно ли описать окружность около параллелограмма? Прямоугольника? Ромба? Почему?
-
Может ли вписанный в окружность четырехугольник иметь равные стороны, но неравные углы? Почему?
-
Может ли вписанный в окружность многоугольник иметь равные углы, но неравные стороны? Почему?
-
Можно ли описать окружность около пятиугольника с углами 800, 900, 1000, 1300, 1400? Почему?
-
Какой четырехугольник называется дельтоидом? Перечислите его свойства.
-
Устная работа
-
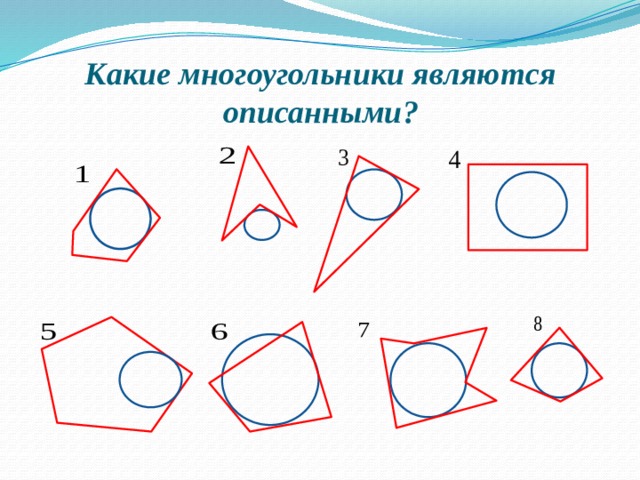
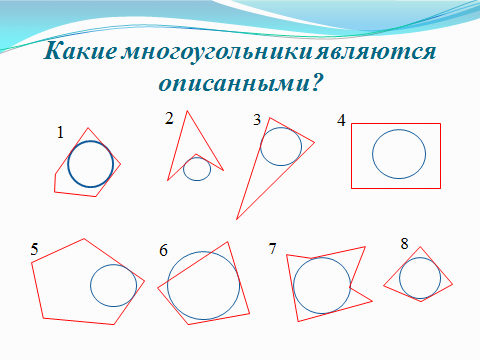
Внимательно рассмотрите рисунки (слайд 2). Как вы думаете, какие многоугольники являются описанными около окружности. Почему вы так решили?
-
Как можно назвать стороны этих четырехугольников по отношению к окружности?
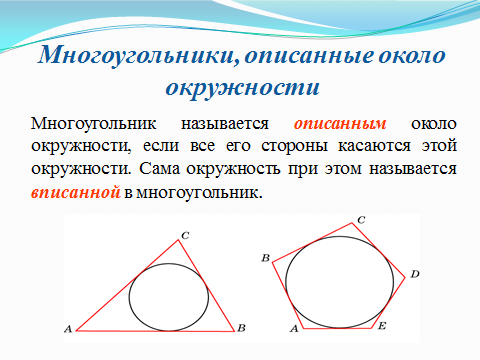
III.Учебно-познавательная деятельность.
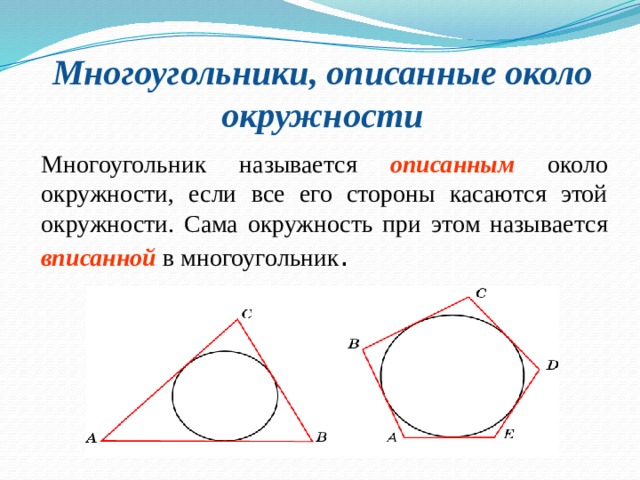
Перейдем теперь к рассмотрению описанных многоугольников. Ситуация здесь в некотором смысле двойственная по отношению к вписанным многоугольникам. При этом стороны описанного многоугольника двойственны углам вписанного многоугольника. Так, например, если для вписанного четырехугольника необходимым и достаточным условием является равенство сумм противолежащих углов, то для описанного выпуклого четырехугольника необходимым и достаточным условием является равенство сумм противоположных сторон. А именно, имеют место следующие теоремы.
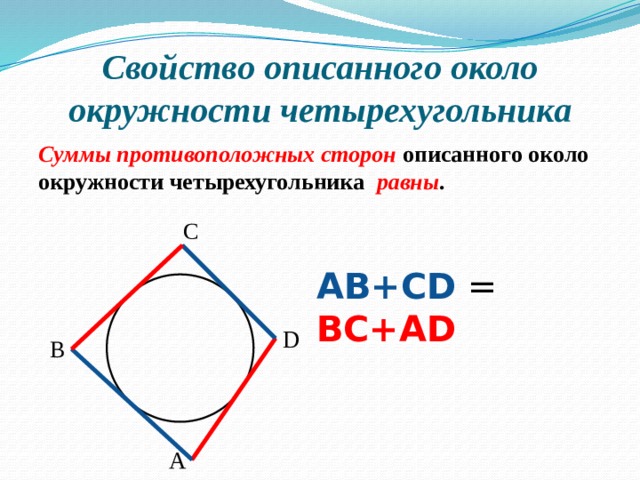
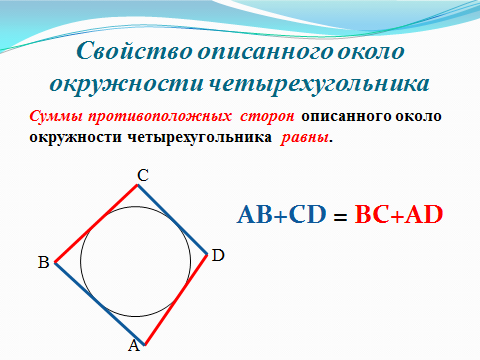
Теорема 1 (свойство сторон описанного четырехугольника)
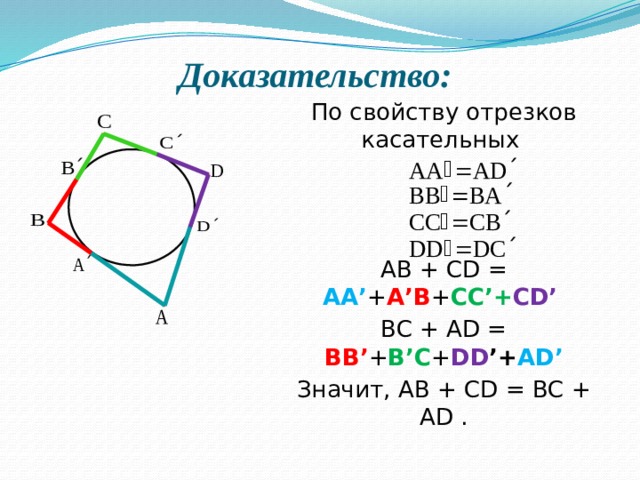
Суммы противоположных сторон описанного около окружности четырехугольника равны (слайды 4,5 разработала группа наиболее подготовленных учащихся класса в качестве домашней работы к уроку)
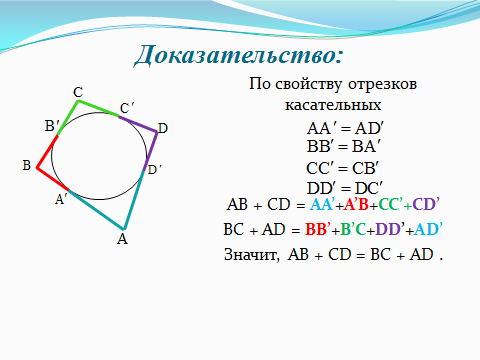
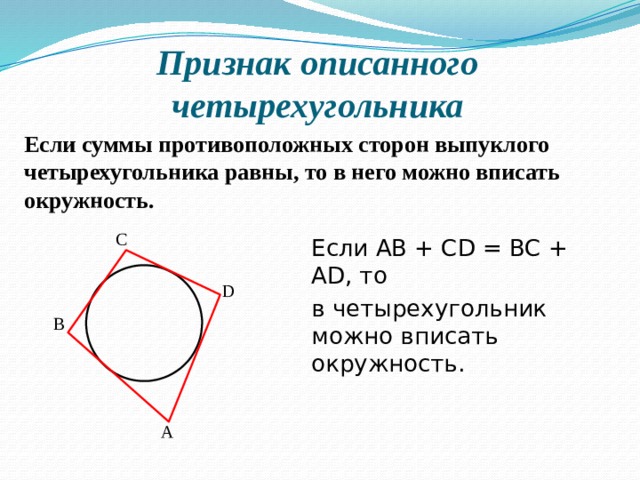
Теорема 2 (признак четырехугольника, в который можно вписать окружность)
Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность (слайд 6 разработала группа наиболее подготовленных учащихся класса в качестве домашней работы к уроку). Учащимся предлагается самостоятельно разобрать доказательство по учебнику (работа с учебником в течение 5 минут, после чего учащиеся могут задавать вопросы по доказательству).
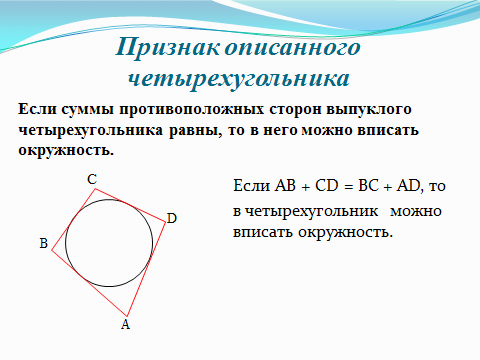
Замечание: в процессе разбора доказательства теорем группа учащихся, самостоятельно разбиравших дома теоремы и готовивших слайды к презентации выполняют индивидуальные задания. Каждому ученику выдаётся карточка с планом исследования . Выполняя задания в соответствии с этим планом, ученики все промежуточные действия и конечные выводы записывают в тетрадях. (Приложение 2)
IV. Решение задач.
-
Устная работа
-
Можно ли вписать окружность в прямоугольник?
-
Можно ли вписать окружность в квадрат?
-
Можно ли вписать окружность в ромб?
-
Можно ли вписать окружность в параллелограмм?
-
В какие ещё четырехугольники можно вписать окружность?
-
При каком условии можно вписать окружность в трапецию?
-
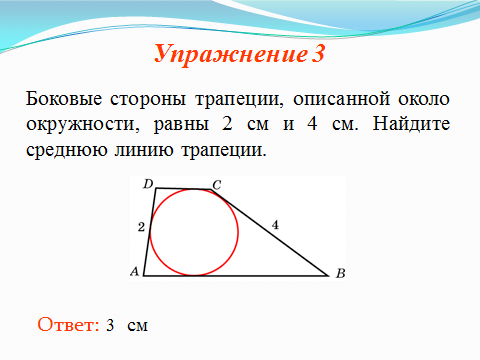
Задачи слайдов 7 – 11.
Раздается таблица «Примеры описанных четырехугольников»
-
Письменная работа (решение задач по готовым чертежам (слайды 12 – 13))
Замечание: дети делятся на две группы: I группа проходит тестирование на компьютере (Приложение 3), другая группа решает задачи совместно с учителем, на тест выделяется по 5 минут, по окончании работы группы меняются местами).
V. Домашнее задание.
Учебник Л.С. Атанасян и др. №696, №697, №698, №700
Геометрия. Дополнительные главы к учебнику: пункт 59 (Теорема Птолемея) разобрать самостоятельно (слайд 14)

Историческая справка (слайд 15)

VI. Итоги урока, рефлексия.
Что нового узнали сегодня на уроке? Чему научились? На какой ступеньке освоения темы вы находитесь? (слайд 16)

Вы все прошли компьютерный тест. Сейчас я предлагаю вам оценить качество работы на уроке. Если вы набрали 9 – 12 баллов – отметка «5»
6 – 8 баллов – отметка «4»
3 – 5 баллов – отметка «3»
Ну а те, кто выполнил менее 3 заданий, сделайте соответствующие выводы, попробуйте установить причину, по которой вы не справились с заданием и устранить её.
Приложение 1. Примеры описанных четырехугольников
| Фигура | Рисунок | Утверждение |
| Ромб | 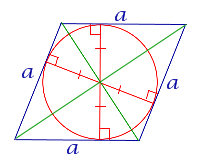
| В любой ромб можно вписать окружность |
| Квадрат | 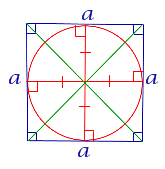
| В любой квадрат можно вписать окружность |
| Прямоугольник | 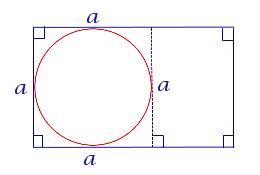
| В прямоугольник можно вписать окружность тогда и только тогда, когда он является квадратом |
| Параллелограмм | 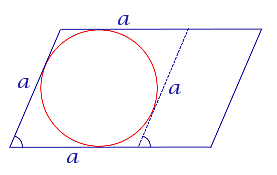
| В параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом |
| Дельтоид | 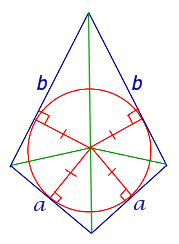
| В любой дельтоид можно вписать окружность |
| Трапеция | 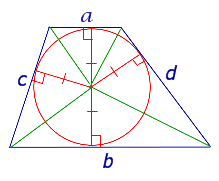
| В трапецию можно вписать окружность тогда и только тогда, когда у трапеции сумма длин боковых сторон рана сумме длин оснований |
Приложение 2. Задания для творческой группы
-
Приведите пример невыпуклого четырехугольника, у которого суммы противоположных сторон равны, и в который нельзя вписать окружность.
-
Исследовательская работа по карточке.
| План исследования Конечная цель: сформулировать и доказать гипотезу Ход исследования. I этап (индивидуальная работа) -
Начертить пятиугольник, описанный около окружности. -
Найти сумму любых двух несоседних сторон. -
Найдите сумму трех оставшихся сторон пятиугольника. -
Сравните результаты, полученные в пунктах 2 и 3. II этап (коллективная работа) -
Сравните результаты, полученные в пункте 4. -
Выдвинете гипотезу. -
Докажите гипотезу или опровергнете, приведя контрпример.
|
Приложение 3. Тестирование на компьютере
-
Центр описанной около треугольника окружности совпадает с точкой пересечения его:
-
биссектрис
-
серединных перпендикуляров
-
высот
-
медиан
-
Окружность называется вписанной в многоугольник, если:
-
Все его вершины лежат на окружности
-
Все его стороны имеют общие точки с окружностью
-
Все его стороны являются отрезками касательных к окружности
-
Все его стороны касаются окружности
-
В равносторонний треугольник вписана окружность радиуса 4 см. чему равна сторона треугольника?
-
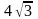 см
см
-
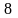 см
см
-
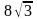 см
см
-
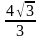 см
см
-
Четырехугольник АВСD описан около окружности. 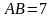 см,
см,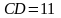 см, ВС в 2 раза меньше АD. Найти длину ВС.
см, ВС в 2 раза меньше АD. Найти длину ВС.
-
6 см
-
22 см
-
12 см
-
14 см
-
Равнобедренный треугольник с высотой, проведенной к основанию и равной 16 см, вписан в окружность радиуса 10 см. найти площадь этого треугольника.

Площадь треугольника = см2
-
В прямоугольном треугольнике АВС (угол С равен 900) АС+ВС=17 см, радиус вписанной в него окружности равен 2 см. Найдите площадь этого треугольника.

Площадь треугольника = см2
Приложение 4. Задачи для классной работы
-
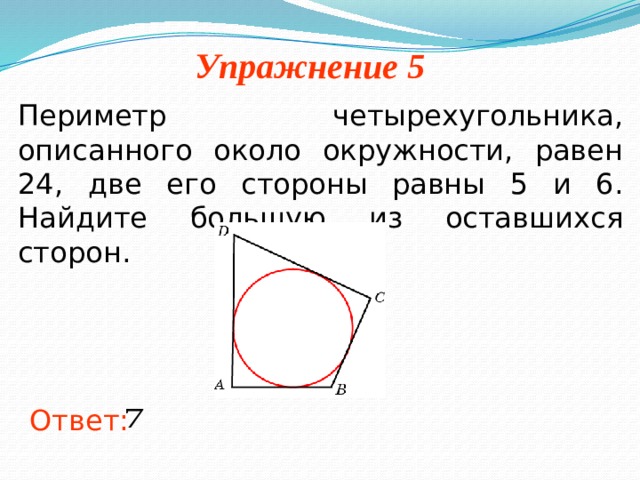
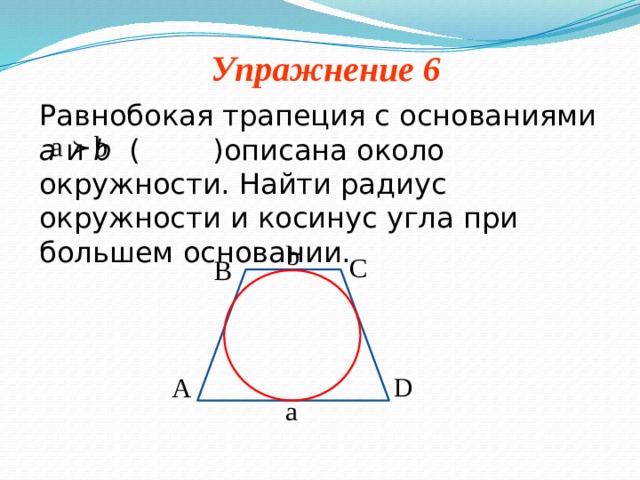
Равнобокая трапеция с основаниями а и b (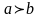 )описана около окружности. Найти радиус окружности и косинус угла при большем основании.
)описана около окружности. Найти радиус окружности и косинус угла при большем основании.
-
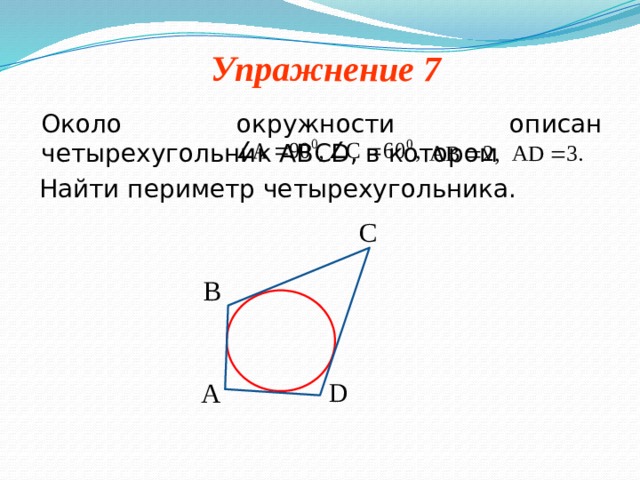
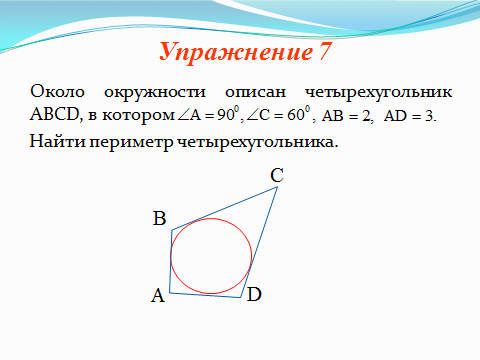
Около окружности описан четырехугольник ABCD , в котором 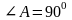 ,
, 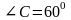 , АВ = 2, АD = 3. Найти периметр четырехугольника.
, АВ = 2, АD = 3. Найти периметр четырехугольника.


























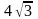 см
см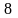 см
см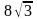 см
см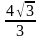 см
см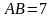 см,
см,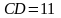 см, ВС в 2 раза меньше А
см, ВС в 2 раза меньше А

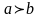 )описана около окружности. Найти радиус окружности и косинус угла при большем основании.
)описана около окружности. Найти радиус окружности и косинус угла при большем основании.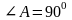 ,
, 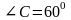 , АВ = 2, А
, АВ = 2, А