К началу учебного года! Готовые материалы для учителей на каждый урок со скидкой от 30%

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ

Благодаря готовым учебным материалам для работы в классе и дистанционно

Выбрать материалы

Скидки до 50 % на комплекты
только до

Готовые ключевые этапы урока всегда будут у вас под рукой

Организационный момент

Проверка знаний

Объяснение материала

Закрепление изученного

Итоги урока

Была в сети 02.09.2025 18:17

Негоднева Татьяна Михайловна

учитель математики

61 год

22 164

1 342

Подписчики

Подписки

Местоположение

Россия, Нефтекумск

Специализация

Математика

Внеурочка

Классному руководителю

Всем учителям

Обо мне Блог Файлы Тесты Галерея Активность Награды

Разработки 15 вариантов по математике ОГЭ

Категория: Математика

10.01.2017 19:46

Данный материал содержит 15 вариантов кимов по математике.К каждому варианту есть решения в торой части и критерии оценивания .

Просмотр содержимого документа
«Критерии оценивания 2 части»

Баллы	Критерии оценки выполнения задания
2	Обоснованно получен верный ответ
1	Решение доведено до конца, но допущена описка или ошибка вычислительного характера, с её учётом дальнейшие шаги выполнены верно
0	Другие случаи, не соответствующие указанным критериям
2	Максимальный балл

Задание 21

Задание 22

Баллы	Критерии оценки выполнения задания
2	Ход решения задачи верный, получен верный ответ
1	Ход решения верный, все его шаги присутствуют, но допущена описка или ошибка вычислительного характера
0	Другие случаи, не соответствующие указанным критериям
2	Максимальный балл

Задание 23

Баллы	Критерии оценки выполнения задания
2	График построен верно, верно найдены искомые значения параметра
1	График построен верно, но искомые значения параметра найдены неверно или не найдены
0	Другие случаи, не соответствующие указанным критериям
2	Максимальный балл

Задание 24

Баллы	Критерии оценки выполнения задания
2	Ход решения верный, все его шаги выполнены правильно, получен верный ответ
1	Ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка
0	Другие случаи, не соответствующие указанным критериям
2	Максимальный балл

Задание 25

Баллы	Критерии оценки выполнения задания
2	Доказательство верное, все шаги обоснованы
1	Доказательство в целом верное, но содержит неточности
0	Другие случаи, не соответствующие указанным критериям
2	Максимальный балл

Задание 26

Баллы	Критерии оценки выполнения задания
2	Ход решения задачи верный, получен верный ответ
1	Ход решения верный, все его шаги присутствуют, но допущена описка или ошибка вычислительного характера
0	Другие случаи, не соответствующие указанным критериям
2	Максимальный балл

Просмотр содержимого документа
«Шкала пересчета первичного балла за выполнение экзаменационной работы в отметку по пятибалльной шкале»

Шкала пересчета первичного балла за выполнение экзаменационной работы в отметку по пятибалльной шкале.

Математика.

2016 год.

Максимальное количество баллов, которое может получить экзаменуемый за выполнение всей экзаменационной работы, - 32 балла. Из них - за модуль «Алгебра» - 14 баллов, за модуль «Геометрия» - 11 баллов, за модуль «Реальная математика» - 7 баллов.
Рекомендуемый минимальный результат выполнения экзаменационной работы, свидетельствующий об освоении федерального компонента образовательного стандарта в предметной области «Математика», - 8 баллов, набранные в сумме за выполнение заданий всех трёх модулей, при условии, что из них не менее 3 баллов по модулю «Алгебра», не менее 2 баллов по модулю «Геометрия» и не менее 2 баллов по модулю «Реальная математика». Преодоление этого минимального результата даёт выпускнику право на получение, в соответствии с учебным планом образовательного учреждения, итоговой отметки по математике или по алгебре и геометрии.
Рекомендованные шкалы пересчёта первичного балла в экзаменационную отметку по пятибалльной шкале:
суммарного балла за выполнение работы в целом - в экзаменационную отметку по математике (табл. 2);
суммарного балла за выполнение заданий, относящихся к разделу «Алгебра» (все задания модуля «Алгебра» и задания 14, 15, 16, 18, 19, 20 модуля «Реальная математика»), - в экзаменационную отметку по алгебре (табл. 3);
суммарного балла за выполнение заданий, относящихся к разделу «Геометрия» (все задания модуля «Геометрия» и задание 17 модуля «Реальная математика»), - в экзаменационную отметку по геометрии (табл. 4).

Таблица 2
Шкала пересчёта суммарного балла за выполнение экзаменационной работы в целом в отметку по математике

0—7 баллов — отметка «2»
8—14 баллов — отметка «3»
15—21 баллов — отметка «4»
22—32 баллов — отметка «5»

Таблица 3
Шкала пересчета суммарного балла за выполнение заданий, относящихся к разделу «Алгебра» в отметку по алгебре

0—4 баллов — отметка «2»
5—10 баллов — отметка «3»
11—15 баллов — отметка «4»
16—20 баллов — отметка «5»

Таблица 4
Шкала пересчета суммарного балла за выполнение заданий, относящихся к разделу «Геометрия» в отметку по геометрии

0—2 баллов — отметка «2»
3—4 баллов — отметка «3»
5—7 баллов — отметка «4»
8—12 баллов — отметка «5»

Просмотр содержимого документа
«ответы Вариант 09001-09015 на вторую часть»

ОТВЕТЫ на 2 часть

Вариант 09001(09006, 09011)

Задание 21 . Один из корней уравнения равен . Найдите второй корень.

Решение.

Подставим известный корень в уравнение: . Получим уравнение относительно . Решим его: . Подставим уравнение: , откуда

Ответ:

Задание 22 . Расстояние между пристанями А и В равно 80 км. Из А в В по течению реки отправился плот, а через 2 часа вслед за ним отправилась яхта, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот прошел 22 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в км/ч.

Решение.

Обозначим искомую скорость (в км/ч) за . Плот прошёл 22 км, значит, он плыл 11 часов, а яхта 9 часов. Таким образом, имеем:

откуда находим .

Ответ: 18 км/ч.

Задание 23 . Постройте график функции и определите, при каких значениях параметра прямая имеет с графиком ровно одну общую точку.

Решение.

График функции изображён на рисунке.

Прямая будет иметь с графиком единственную общую точку при

Ответ: (−1;0].

Задание 24 . Окружность, вписанная в треугольник ABC , касается его сторон в точках M, K иP. Найдите углы треугольника ABC, если углы треугольника MKP равны 49°, 69° и 62°.

Решение.

Пусть

∠BAC = α , ∠ABC = β , ∠ACB = γ;

∠PKM = 49°, ∠MPK = 69°, ∠KMP = 62°.

По свойству касательных AM = AP, BM = BK , CP = CK . Значит, треугольники AMP, BMK и CPK равнобедренные, откуда получаем:

Значит, Аналогично получаем, что и

Решая систему относительно α , β и γ , получаем, что углы треугольника ABC равны 82°, 42°, 56°.

Ответ: 82°, 42°, 56°.

Задание 25 . В окружности с центром О проведены две хорды АВ и CD так, что центральные углы АОВ и СОD равны. На эти хорды опущены перпендикуляры ОК и OL. Докажите, что ОК и OLравны.

Решение.

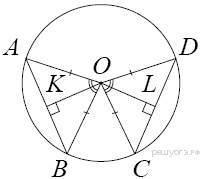Треугольники АОВ и СОD равны по двум сторонам и углу между ними (AO = BO = CO = DO как радиусы окружности, ∠AOB = ∠COD по условию). Следовательно, высоты OK и OL равны как соответственные элементы равных треугольников.

Задание 26 . Основание равнобедренного треугольника равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания в его середине . Найдите радиус окружности, вписанной в треугольник .

Решение.

Пусть — центр данной окружности, а — центр окружности, вписанной в треугольник . Точка касания окружностей делит пополам. и — биссектрисы смежных углов, значит, угол прямой. Из прямоугольного треугольника получаем:

Следовательно,

Ответ: 4,5.

Вариант 09002( 09007, 09012)

Задание 21 . Решите уравнение:

Решение.

Раскладывая на множители левую часть уравнения, получаем Таким образом, корни уравнения

Ответ:

Задание 22 . Моторная лодка прошла 36 км по течению реки и вернулась обратно, потратив на весь путь 5 часов. Скорость течения реки равна 3 км/ч. Найдите скорость лодки в неподвижной воде.

Решение.

Обозначим км/ч искомую скорость. По течению реки лодка двигалась ч.
Против течения лодка шла ч. Получаем уравнение

Решим его:

Корни квадратного уравнения: 15 и −0,6. Следовательно, скорость лодки равна 15 км/ч.

Ответ: 15 км/ч.

Задание 23 . Постройте график функции и найдите все значения , при которых прямая не имеет с графиком данной функции общих точек.

Решение.

Найдём область определения функции:

и .

Значит, функция определена при .

Поскольку , получаем, что на области определения функция принимает вид . График изображён на рисунке.Прямая не имеет с графиком данной функции общих точек при .

Ответ: .

Задание 24 . Окружность с центром на стороне AC треугольника ABC проходит через вершинуC и касается прямой AB в точке B . Найдите диаметр окружности, если AB =15, AC = 25.

Решение.

Пусть DC = x. Тогда по свойству касательной и секущей, проведённых из одной точки к окружности, получаем:

AB² = AC(AC − x); 225 = 25(25 − x), откуда x = 16.

Ответ: 16.

Задание 25 . Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3 : 5 : 10. Найдите радиус окружности, если меньшая из сторон равна 19.

Решение.

Пусть длины дуг AB, BC и AC относятся как 3 : 5 : 10, тогда наименьшая сторона треугольника ABC — сторона AB = 19. По свойству вписанного угла

Из теоремы синусов находим, что радиус окружности равен

Ответ: 19.

Задание 26 . Три окружности с центрами и и радиусами 2,5; 0,5 и 4,5 соответственно попарно касаются внешним образом. Найдите угол

Решение.

Из условия касания окружностей находим стороны треугольника

По теореме косинусов

Откуда

Ответ: 120°.

Вариант 09003( 09008, 09013)

Задание 21 . Решите уравнение:

Решение.

Сделаем замену    Получаем уравнение
Корни:
Если , то    или
Если , то    или

Ответ:

Задание 22 . Катер прошёл от одной пристани до другой, расстояние между которыми по реке равно 48 км, сделал стоянку на 20 мин и вернулся обратно через после начала поездки. Найдите скорость течения реки, если известно, что скорость катера в стоячей воде равна 20 км/ч.

Решение.

Пусть скорость течения реки равна км/ч. Тогда скорость катера по течению реки равна км/ч, а против течения — км/ч. Время движения катера по течению реки равно , а против течения — по смыслу задачи Весь путь занял . Составим и решим уравнение:

Тем самым, скорость течения реки равна 4 км/ч.

Ответ: 4 км/ч.

Задание 23 . Постройте график функции

и определите, при каких значениях прямая имеет с графиком ровно две общие точки.

Решение.

График функции состоит из двух лучей и отрезка.На рисунке видно, что график имеет ровно две общих точки с горизонтальными прямыми и .

Ответ: 1; −2.

Задание 24 . В треугольнике ABC угол С равен 90°, радиус вписанной окружности равен 2. Найдите площадь треугольника ABC, если AB = 12.

Решение.

Пусть A₁, B₁ и C₁ — точки касания вписанной окружности со сторонами BC, AC и AB соответственно. Радиус вписанной окружности обозначим r. Тогда AC₁ = AB₁ и CA₁ = CB₁ = r. Периметр треугольника ABC равен 2AC₁ + 2BC₁ + 2CA₁ = 2AB + 2r. Полупериметр p равен AB + r.

По формуле площади треугольника находим

Ответ: 28.

Задание 25 . В окружности с центром проведены две равные хорды и . На эти хорды опущены перпендикуляры и . Докажите, что и равны.

Решение.

Проведем ОK, ON, OL, OM — радиусы. Треугольники KOL и MON равны по трем сторонам, тогда высоты OH и OS также равны как элементы равных треугольников. Что и требовалось доказать.

Задание 26 . В треугольнике угол равен 120°, а длина стороны на меньше полупериметра треугольника. Найдите радиус окружности, касающейся стороны и продолжений сторон и .

Решение.

Центр окружности является точкой пересечения биссектрис углов и . При этом по свойству касательных . Следовательно, длины ломаных и равны полупериметру . По условию .

Найдем радиус из прямоугольного треугольника . В треугольнике

катет лежит против угла 30°, значит,

Ответ: 3.

Вариант 09004(09009, 09014)

Задание 21 . Решите уравнение

Решение.

Последовательно получаем:

Ответ: −1; 2; 6.

Задание 22 . На изготовление 231 детали ученик тратит на 11 часов больше, чем мастер на изготовление 462 таких же деталей. Известно, что ученик за час делает на 4 детали меньше, чем мастер. Сколько деталей в час делает ученик?

Решение.

Предположим, что ученик делает деталей в час. Тогда мастер делает детали в час.
На изготовление 231 детали ученик потратит ч, а мастер тратит ч на изготовление 462 деталей.
Составим уравнение по условию задачи:

Решим уравнение:

Корни полученного квадратного уравнения: −28 и 3. Отбрасывая отрицательный корень, находим, что ученик делает в час 3 детали.

Ответ: 3.

Задание 23 . Постройте график функции

и определите, при каких значениях прямая будет пересекать построенный график в трёх точках.

Решение.

Построим график функции (см. рисунок).

Из графика видно, что прямая будет иметь с графиком ровно три точки пересечения при принадлежащем множеству:

Ответ: (0; 5).

Задание 24 . Точка H является основанием высоты BH, проведённой из вершины прямого углаB прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK = 20.

Решение.

Угол PBK опирается на дугу PK и равен 90°, а значит, PK — диаметр, откуда получаем, что BH =PK = 20.

Задание 25 . Сторона BC параллелограмма ABCD вдвое больше стороны CD. Точка L — середина стороны BC. Докажите, что DL — биссектриса угла CDA.

Решение.

Проведём LF параллельно CD (см. рис.). Тогда BL = LC = CD. Следовательно, параллелограмм CDFL является ромбом. Диагональ DL ромба CDFL является биссектрисой угла CDA.

Задание 26 . Две касающиеся внешним образом в точке K окружности, радиусы которых равны 16 и 48, вписаны в угол с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.

Решение.

Пусть Q — центр большей окружности, а O — центр меньшей, QM и ON — радиусы, проведённые в точки касания окружностей с прямой AC , S — центр окружности, описанной около треугольника ABC , r — радиус окружности, описанной около треугольника ABC .

Поскольку BC и AB — общие касательные к окружностям, BO и BQ — биссектрисы углов ABK и смежного с ним. Значит, угол OBQ прямой, следовательно, из треугольника OBQ находим, что

Пусть AN = x. Прямоугольные треугольники ANO и AMQ подобны с коэффициентом 3, значит,AM = 3x , MN = 2x.

Отрезки MC , CK и CN равны как отрезки касательных, проведённых из одной точки, значит, , , откуда .

В прямоугольном треугольнике ABK находим неизвестный катет:

В прямоугольном треугольнике SBK по теореме Пифагора имеем

;

Ответ: 32.

Вариант 09005(09010, 09015)

Задание 21 . Решите уравнение

Решение.

Последовательно получаем:

Поскольку подкоренное выражение не может быть меньше нуля, область допустимых значений исходного уравнения ограничивается неравенством значит, решением уравнения является только

Ответ: −2.

Задание 22 . Два оператора, работая вместе, могут набрать текст газеты объявлений за 8 ч. Если первый оператор будет работать 3 ч, а второй 12 ч, то они выполнят только 75% всей работы. За какое время может набрать весь текст каждый оператор, работая отдельно?

Решение.

Пусть первый оператор может выполнить данную работу за часов, а второй за часов. За один час первый оператор выполняет часть всей работы, а второй . Составим систему уравнений:

Ответ: первый оператор за 12 ч, второй оператор за 24 ч.

Задание 23 . Постройте график функции и определите, при каких значениях прямая имеет с графиком ровно три общие точки.

Решение.

Раскрывая модуль, получим, что график функции можно представить следующим образом:

Этот график изображён на рисунке:

Из графика видно, что прямая имеет с графиком функции ровно три общие точки при и

Ответ: 0; 1.

Задание 24 . В треугольнике АВС углы А и С равны 20° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.

Решение.

Найдем

Так как BD - биссектриса, то

Треугольник HBC- прямоугольный. Так как то

Таким образом, искомый угол DBH равен

Ответ:

Задание 25 . В треугольнике ABC с тупым углом ABC проведены высоты AA₁ и CC₁. Докажите, что треугольники A₁BC₁ и ABC подобны.

Решение.

Поскольку угол ABC тупой, основания высот будут лежать на продолжениях сторон. Так как диагонали четырёхугольника AA₁C₁C пересекаются, он выпуклый, а поскольку около него можно описать окружность. Тогда как вписанные углы, опирающиеся на дугу CC₁, а как вписанные углы, опирающиеся на дугу CC₁. Значит, указанные треугольники подобны по двум углам.

Задание 26 . В прямоугольном треугольнике катет равен 8, катет равен 15. Найдите радиус окружности, которая проходит через концы гипотенузы треугольника и касается прямой .

Решение.

По условию окружность проходит через точку и это единственная общая точка окружности и прямой . Следовательно, радиус окружности перпендикулярен прямой . Поэтому прямые и параллельны. Центр окружности равноудален от точек и , следовательно, он лежит на серединном перпендикуляре к . Обозначим середину буквой .

— это накрест лежащие углы при параллельных прямых и секущей .

Следовательно, прямоугольные треугольники и подобны.

По теореме Пифагора найдем, что . Коэффициент подобия равен

Тогда

Ответ: .

Просмотр содержимого документа
«ответы на кимы»

Но- мер зада- ния	Ответы на вариант
Но- мер зада- ния	09001	09002	09003	09004	09005	09006	09007	09008	09009	09010	09011	09012	09013	09014	09015
1	3,91	-0,3	5,9	1,6	12,5	4,4	270	−550	−320	−30	4	3	−30	3,2.	-0,3
2	3	3	2	2	1	1	1	3	4	4	3	2	4	4	3
3	1	220	1	3	4	4	3	2	1	3	1	2	3	3	2
4	−2; 3	−4; 1	0; 5	3	−2,5	22	4	−4,5	2	9,7	0,6; 6	−2,5	9,7	1,5	−3
5	23	1423	3	12	23	−1	4	142	1	3	2	431	4123	413	314
6	32	1088	−1364	−7	−172	50	4	7	54	21	-250	46	-11	28,7	-53,6
7	-1	0,4	0,25	16	5,6	0	−230,4	-60	1,9	5	0,29	-1	0,25	5,6	-60
8	1	4	4	1	4	4	2	3	4	1	3	2	4	4	4
9	65	60	122	30	66	45	3	110	120	5	4	20	50	40	78
10	30	17,5	85	6084	4	6	71	6,5	24	35	315	22	57,5	42	6,5
11	100	100	27556	120	25	2688	50	8	25	12	480	168	36	17	15
12	0,4	0,75	10	3	1,5	1	40	5	2	11	4	2	0,4	1	2,5
13	12или21	13или31	23или32	12или21	3	24 или42	12или 21	13или31	23или32	23или32	12или21	23или32	13или31	13или31	12или21
14	4	2	3	3	4	1	3	3	4	3	3	2	2	4	2
15	38	14	30	23	34	16	15	134	23	4	1	12	23	13	13
16	75	80	12,25	40	2	250	10	844	40	1980	960	850	57,6	420	12,5
17	13	390	2,9	20	150	60	8	45	2,4	1000	17	1,6	65	2,3	2,45
18	49	15	4	170	2	10	4	3	4	1	3	3	2	49	15
19	0,92	0,56	0,5	0,95	0,3	0,5	0,45	0,995	0,2	0,3	0,013	0,9	0,18	0,6	0,81
20	183	50 500	1,28	3	4	13	3,2	2,25	16	60	3	0,6	1,44	260	238