Кыргызстан, Бишкек
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 07.06.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Был в сети 14.02.2020 13:04
Сабыров Руслан Сыдыкович
учитель информатики
47 лет
981
59 041 
Местоположение
Разветвляющие алгоритмы
Категория:
Информатика
29.01.2020 11:59
Просмотр содержимого документа
«Разветвляющие алгоритмы»
|
| ||||||
|
|
Разветвляющиеся алгоритмы
|
|
| В таких алгоритмах делается выбор: выполнять или не выполнять какую-нибудь группу команд в зависимости от условия, т.е. выбирается один из нескольких возможных путей (вариантов) вычислительного процесса. Каждый подобный путь называется ветвью алгоритма. Признаком разветвляющегося алгоритма является наличие операций условного перехода, когда происходит проверка истинности некоторого логического выражения (проверяемое условие) и в зависимости от истинности или ложности проверяемого условия для выполнения выбирается та или иная ветвь алгоритма. В логических выражениях используется операция сравнения: (больше), = (больше или равно), = (равно), (не равно). Часто встречаются задачи, в которых используются не отдельные условия, а совокупность связанных между собой условий (отношений). Для связи используются AND и (или) OR. Например: (2+3) and (2+5) = 6 – нет (ложно) Алгоритм предполагает выполнение Действия 1, если записанное условие истинно (выполняется), и выполнение Действия 2, если условие ложно (не выполняется) – это полная развилка. Полная развилка: If условие then Действие 1 else Действие 2 Если в алгоритме отсутствует Действие 2, т.е. если записанное условие истинно, то выполняется Действие 1, а если условие ложно, то никаких действий не выполняется – это не полная развилка. Неполная развилка: If условие then Действие 1 ПРИМЕР 1. ПРИМЕР 2. ПРИМЕР 3. Дано натуральное число n. Если число нечётное и его удвоение не приведет к выходу за 32767 (двухбайтовое целое число со знаком), удвоить его, иначе – оставить без изменения. Решение: Чтобы удовлетворить условию удвоения, число n должно быть нечетным и меньше 16384. 1. Ввести число n 2. Если число n нечетное и меньше 16384, то n := n * 2 ((N mod 2) =1 and (n) 3. Вывод n 4. Конец
Фрагмент программы на языке Pascal: Write(‘Введите число N ’); Readln(n); If ((N mod 2) =1 and (n n := n * 2 Writeln(‘Число N=’, n);
Рассмотренный пример иллюстрирует неполную развилку. Также следует отметить, здесь логическое выражение, являющееся условием, содержит 2 операнда. ПРИМЕР 4. Ввести целое число. Вывести соответствующий ему символ ASCII-таблицы, либо сообщить, что такого символа нет (0-31 – управляющие коды, затем до 256 – печатаемые символы). program ascii_symbol; var i:word; begin write('Введите целое число: '); readln(i); if (i31) and (i writeln('Соответствующий символ - ', Chr(i)) else writeln('Такого символа нет'); readln end. |
Слова в Pascal
|
|
| Неделимые последовательности знаков алфавита образуют слова, отделенные друг от друга разделителями и несущие определенный смысл в программе. Разделителями могут служить пробелы, символы конца строки или комментарии. Набор слов, используемый в Pascal, можно разделить на три группы: – зарезервированные слова; – стандартные идентификаторы; – идентификаторы пользователя. Зарезервированные слова являются составной частью языка, имеют фиксированное начертание и раз и навсегда определенный смысл. Они не могут изменяться программистом. Зарезервированные слова версии языка Pascal для персональных ЭВМ приведены ниже. Зарезервированные слова версии языка Pascal:
Зарезервированные слова нельзя использовать в качестве имен, вводимых программистом для обозначения величин, и т. д. Группа слов, имеющая определенный смысл, называется словосочетанием. В языке программирования словосочетание, состоящее из слов и символов и задающее правило вычисления некоторого значения, называется выражением. Минимальная конструкция языка, представляющая собой законченную мысль, есть предложение. Если предложение языка программирования задает полное описание некоторого действия, которое необходимо выполнить, оно называется оператором. Предложение, описывающее структуру и организацию данных – объектов языка, над которыми производятся различные действия, называется описанием. Чтобы научиться правильно писать программы для компьютера, необходимо изучить синтаксис языка программирования (правила записи его конструкций) и его семантику (смысл и правила использования этих конструкций). |
Цикл до (с постусловием)
|
|
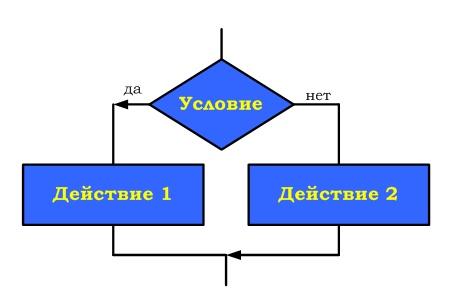
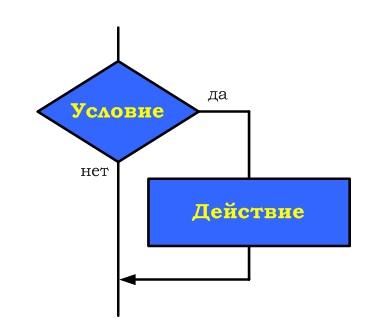
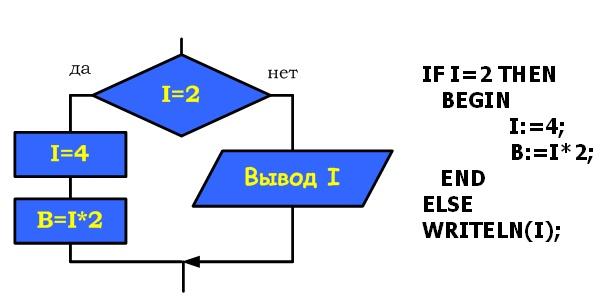
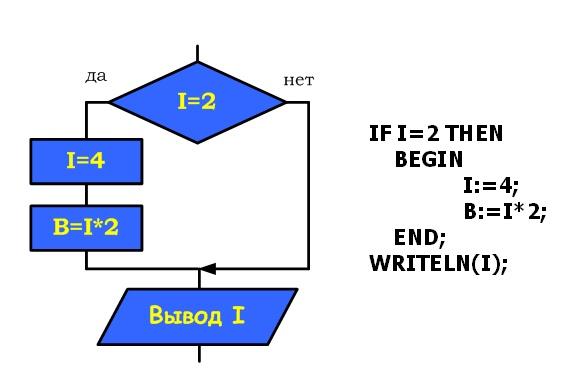
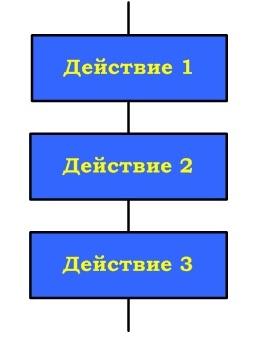
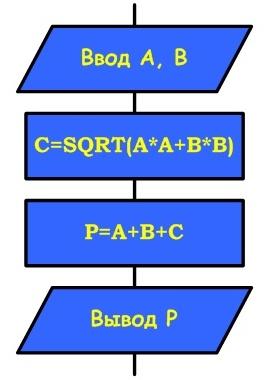
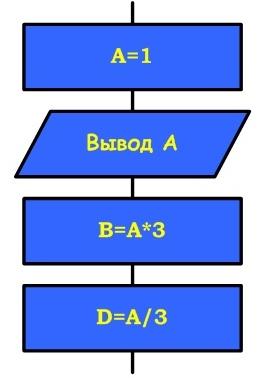
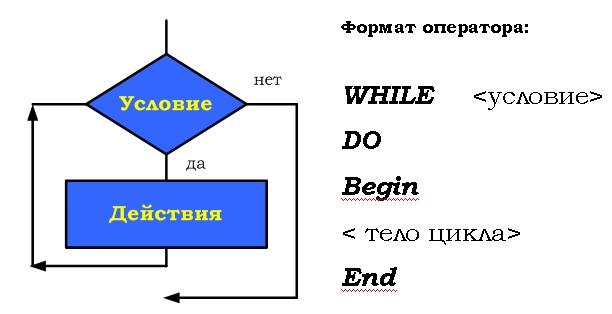
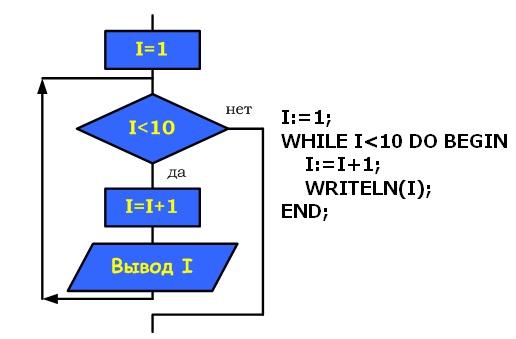
| Цикл предназначен для организации многократного исполнения набора инструкций (операторов, наименьшая автономная часть языка программирования). Если заранее неизвестно число повторений цикла, то можно использовать цикл с постусловием. В большинстве процедурных языков программирования цикл с постусловием реализуется оператором while, отсюда его второе название– while-цикл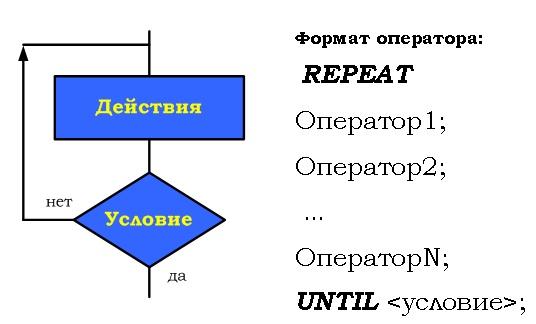
Выполняется следующим образом Сначала выполняется тело цикла, затем проверяется условие. Если оно ложно, то выполняется тело цикла. Если условие истинно, то цикл считается выполненным. В этом цикле логическое выражение - это условие выхода из цикла При описании циклов с постусловием необходимо принимать во внимание следующее: - перед первым выполнением цикла условие его окончания (или продолжения) должно быть определено; - тело цикла должно содержать хотя бы один оператор, влияющий на условие окончания (продолжения), иначе цикл будет бесконечным; - условие окончания цикла должно быть в результате выполнено.
Тело цикла с постусловием выполняется пока условие ложно ПРИМЕР 1. 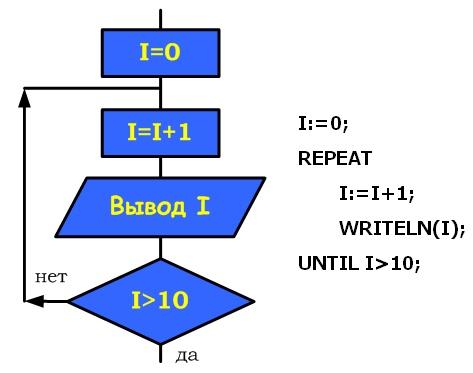ПРИМЕР 2. Пары неотрицательных вещественных чисел вводятся с клавиатуры. Посчитать произведение для каждой пары и сумму всех чисел.
Решение:
program cycle_repeat; var x,y,sum:real; otv:char; begin sum:=0; repeat write('Введите числа x,y 0 '); readln(x,y); writeln('Их произведение = ',x*y:8:3); sum:=sum+x+y; write('Завершить программу (Д/Н)? '); readln(otv); until (otv='Д') or (otv='д'); writeln('Общая сумма = ',sum:8:3); readln end.
ПРИМЕР 3. Подсчитать количество нечетных цифр в записи натурального числа n. Идея решения. Из заданного числа выбирать из младшего разряда цифру за цифрой до тех пор, пока оно не исчерпается, т.е. станет равным нулю. Каждую нечётную цифру учитывать.
Решение:
1. Ввести число n 2. K := 0 {подготавливаем счётчик} 3. Если n mod 10 mod 2 = 1, то K := K +1 4. n := n div 10 5. Если n = 0, переход к шагу 7 6. Переход к шагу 3 7. Вывод K 8. Конец ПРИМЕР 4. Составить программу планирования закупки товара в магазине на сумму, не превышающую заданную величину. Решение Обозначим через x, k – соответствующую цену и количество товара, через p – заданную предельную сумму, через s – общую стоимость покупки. Начальное значение общей стоимости покупки (S) равно нулю. Значение предельной суммы считывается с клавиатуры. Необходимо повторять запрос цены и количества выбранного товара, вычислять его стоимость, суммировать ее с общей стоимостью и выводить результат на экран до тех пор, пока она не превысит предельную сумму р. В этом случае на экран нужно вывести сообщение о превышении. Program E_10; Var x, k, p, s : Integer; Begin WriteLn('Введите цену товара и его количество'); ReadLn(x,k); s:=s+x*k; WriteLn('Стоимость покупки равна ',s); Until sp; WriteLn('Суммарная стоимость покупки превысила предельную сумму'); End. |
Цикл – пока (с предусловием)
|
|
| Циклом называется последовательность действий, выполняемых многократно, каждый раз при новых значениях параметров.
Цикл с предусловием используется, когда неизвестно количество повторений
Выполняется следующим образом: Сначала проверяется условие. Если оно истинно, то выполняется тело цикла. Если условие становится ложным, то тело цикла не выполняется, а выполняется следующий за END оператор. Таким образом, если условие с самого начала ложно, то тело цикла не выполнится ни разу. Для того, чтобы избежать зацикливания программы необходимо обеспечить изменение на каждом шаге цикла значения хотя бы одной переменной, входящей в условие цикла. После выхода из цикла со сложным условием (с использованием операций and, or, xor) как правило, необходима проверка того, по какому условию цикл завершен
Тело цикла с предусловием выполняется пока условие истинно ПРИМЕР 1. ПРИМЕР 2. Пары неотрицательных вещественных чисел вводятся с клавиатуры. Посчитать произведение для каждой пары и сумму всех чисел. program cycle_while; var x,y,sum:real; otv:char; begin sum:=0; otv='Д'; while (otv='Д') or (otv='д') do begin write('Введите числа x,y 0 '); readln(x,y); writeln('Их произведение = ',x*y:8:3); sum:=sum+x+y; write('Завершить программу (Д/Н)? '); readln(otv); end; writeln('Общая сумма = ',sum:8:3); readln end.
ПРИМЕР 3. Нахождение наибольшего общего делителя двух целых чисел с помощью Алгоритма Эвклида. program Evklid; var a,b,c:integer; begin write('введите два целых числа : '); readln(a,b); while b0 do begin c:=a mod b; a:=b; b:=c; end; writeln('наибольший общий делитель = ',a); readln end.
ПРИМЕР 4. Подсчитать количество нечетных цифр в записи натурального числа n. Идея решения. Из заданного числа выбирать из младшего разряда цифру за цифрой до тех пор, пока оно не исчерпается, т.е. станет равным нулю. Каждую нечётную цифру учитывать. 1. Ввести число n 2. K := 0 {подготавливаем счётчик} 3. Если n = 0, переход к шагу 7 4. Если n mod 10 mod 2 = 1, то K := K +1 5. n := n div 10 6. Переход к шагу 3 7. Вывод K 8. Конец
ПРИМЕР 5. Дана последовательность, общий член которой определяется формулой an=(n-1)/(n*n). Вычислить при n2 сумму тех ее членов, которые больше заданного числа k. При решении задачи находится очередной член последовательно и, если он больше k, добавляется к сумме. Решение: 1. Ввести k 2. S := 0 3. A := 1/4 4. n := 3 5. Сравнить А с k. Если A= k, переход к шагу 10 6. S := S + A 7. A := (n-1)/(n*n) 8. n := n + 1 9. Переход к шагу 5 10. Вывод S 11. Конец |
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
