Развитие математической грамотности на уроках "Вероятность и статистика"

Масте р-класс «развитие функциональной грамотности на уроках вероятность и статистика»

Выполнила: учитель математики

МАОУ «Школа № 26 г.Благовещенска»

Пчелинцева Елена Геннадьевна

Под математической функциональной грамотностью следует подразумевать способность личности использовать приобретенные математические знания для решения задач в различных сферах

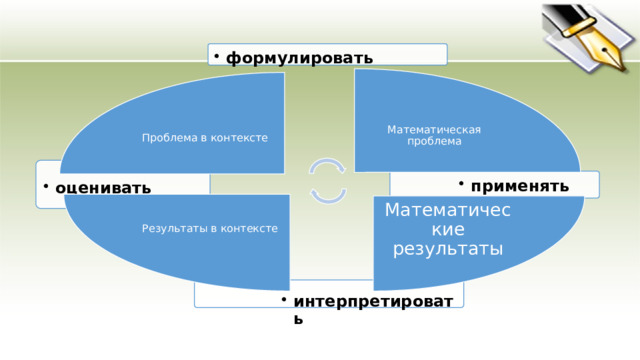
Математическая проблема

Математические результаты

Результаты в контексте

• формулировать
• формулировать

Проблема в контексте

• оценивать
• оценивать

• применять
• применять

• интерпретировать
• интерпретировать

АКТУАЛЬНОСТЬ

• Неэффективная структура содержания (половина учащихся осваивает не более 20% содержания 10—11 классов). Цель математического образования непонятна, а содержание не нужно значительной части общества

• Функциональная математическая грамотность делает более полноценной жизнь россиян в современном обществе…

• Теория вероятностей и статистика – полноценный раздел наряду с алгеброй и геометрией. Вероятность и статистика – связующее звено между школьной математикой и окружающим миром

• В настоящее время теория вероятностей завоевала очень серьезное место в науке и прикладной деятельности.
• В нашу жизнь властно вошли выборы и референдумы, банковские кредиты и страховые полисы, таблицы занятости и диаграммы социологических опросов. Общество все глубже начинает изучать себя и стремиться сделать прогнозы о себе самом и о явлениях природы, которые требуют представлений о вероятности.
• Мы должны научить жить наших детей в вероятностной ситуации, а это, значит, извлекать, анализировать и обрабатывать информацию, принимать обоснованные решения в разнообразных ситуациях со случайными исходами.

• Не так давно было  принято решение ввести этот материал в курс математики основной и средней школы. Внедрение вероятностно-статистической линии в базовый школьный курс математики породило немало проблем. К его появлению оказались не готовы буквально все - от учителей математики до авторов учебников. Мы до сих пор не имеем ни общей концепции преподавания этого раздела математики в школе, ни достаточного количества учебных пособий для школьников, содержащих соответствующий материал.
• При том, что выполнение этих заданий требует наличия у учеников самых элементарных знаний из области теории вероятностей, у многих старшеклассников решение этих задач вызывает серьезные затруднения.

• Задача №4 профильного уровня и задача №10 базового уровня – это задания по теории вероятности. Сегодня мы с вами рассмотрим задачи, для решения которых удобно использовать дерево вероятностей – это простой способ решения некоторых задач.

Про шарики

Из ящика в котором а синих и b красных шаров, наугад вынимают

последовательно один за другим два шара.

А – «первый шар синий» , B – «второй шар синий».

Понятно, что Р(А)=a/(a+b). Какова же вероятность события В?

Если событие А произошло, то среди оставшихся a+b-1 шаров только

а-1 синих, поэтому вероятность того что, что второй шар синий,

(а-1)/(a+b-1). Если же А не произошло, то среди оставшихся шаров синих a, поэтому вероятность того, что второй шар синий, а/(a+b-1). Мы столкнулись с ситуацией, когда вероятность события В зависит от того, произошло ли событие А. В таком случае говорим, что событие В зависит от события А, а вероятность появления события В условная.

• Рассмотрим две задачи на извлечение шаров из урны.
• Задачу №1, решается с помощью классического определение вероятности.
• А вот для того, чтобы решить задачу №2, надо построить дерево вероятностей (граф)

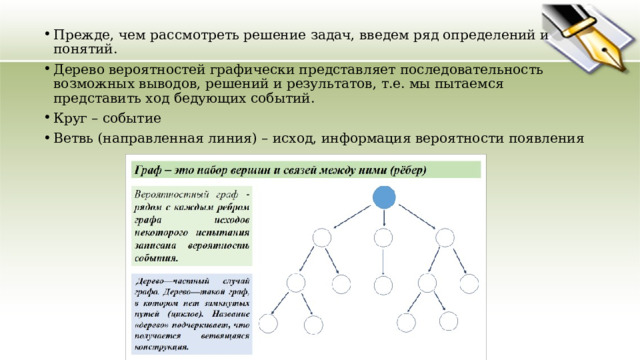
• Прежде, чем рассмотреть решение задач, введем ряд определений и понятий.
• Дерево вероятностей графически представляет последовательность возможных выводов, решений и результатов, т.е. мы пытаемся представить ход бедующих событий.
• Круг – событие
• Ветвь (направленная линия) – исход, информация вероятности появления

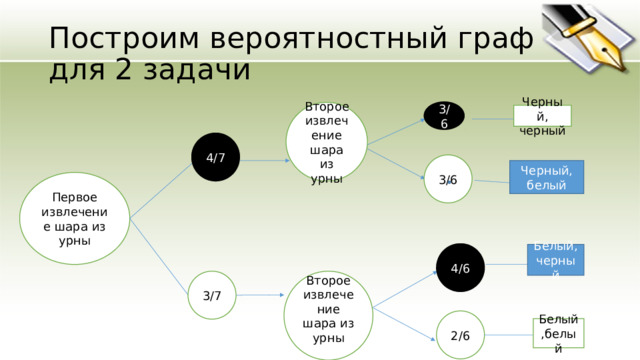
Построим вероятностный граф для 2 задачи

3/6

Второе извлечение шара из урны

Черный, черный

4/7

3/6

Черный, белый

Первое извлечение шара из урны

4/6

Белый, черный

Второе извлечение шара из урны

3/7

2/6

Белый,белый

• Напишем около каждого ребра вероятность:
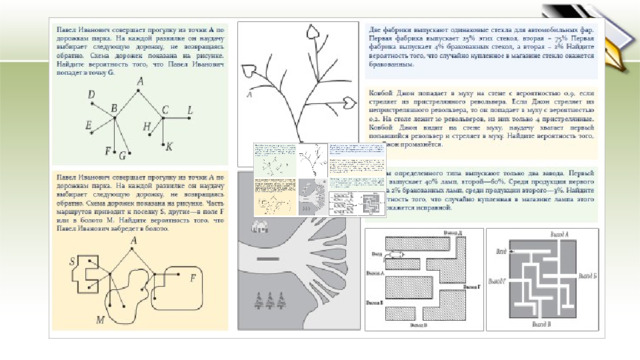
• - Из точки А ведут две дорожки, поэтому вероятность того, что Павел Иванович выберет дорожку АВ или дорожку АС равна .
• - Из точки В – четыре дорожки – вероятность из точки С – три дорожки – вероятность .
• -В точку G попадет, если он пройдет дорожку АВ ( И ) дорожку BG. Вероятность находится умножением вероятностей вдоль дорожек.
• -Результат

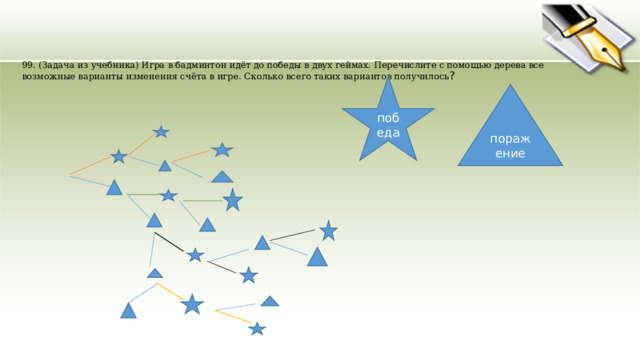
99. (Задача из учебника) Игра в бадминтон идёт до победы в двух геймах. Перечислите с помощью дерева все возможные варианты изменения счёта в игре. Сколько всего таких вариантов получилось ?

победа

поражение

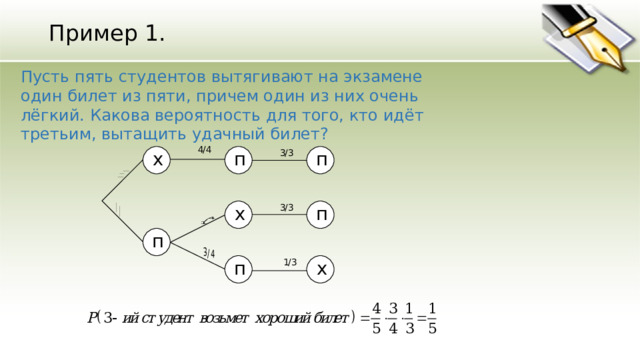
Пример 1.

Пусть пять студентов вытягивают на экзамене один билет из пяти, причем один из них очень лёгкий. Какова вероятность для того, кто идёт третьим, вытащить удачный билет?

Пример 2.

Имеются 2 урны с шарами. В первой урне находятся 2 белых и 4 черных шара, во второй – 3 белых и 3 черных.

• Из каждой урны достали по одному шару. Найти вероятность того, что эти шары белые.
• Выбирается урна и из нее извлекается 2 шара. Найти вероятность того, что эти шары белые. Найти вероятность того, что они были взяты из первой урны.
• Из первой урны во вторую переложили 1 шар, а затем из второй (пополненной) урны достали 2 шара. Они оказались белыми. Найти вероятность того, что был переложен белый шар.

3/5

3/6

2/5

3/6

3/6

3/6

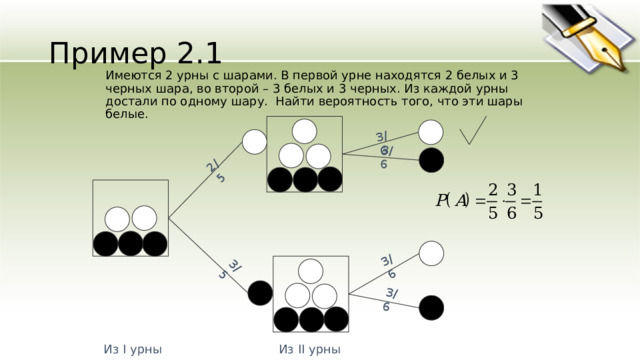
Пример 2.1

Имеются 2 урны с шарами. В первой урне находятся 2 белых и 3 черных шара, во второй – 3 белых и 3 черных. Из каждой урны достали по одному шару. Найти вероятность того, что эти шары белые.

Из I урны

Из II урны

1/2

1/2

3/6

3/6

3/5

1/4

2/5

2/4

2/4

2/5

3/5

2/5

3/4

Пример 2.2

Имеются 2 урны с шарами. В первой урне находятся 2 белых и 3 черных шара, во второй – 3 белых и 3 черных. Выбирается урна и из нее извлекается 2 шара. Найти вероятность того, что эти шары белые. Найти вероятность того, что они были взяты из первой урны.

3/5

3

2/6

4/6

4/7

3/7

3/7

4/7

3/6

3/6

4/6

2/6

2/6

4/6

3/6

3/6

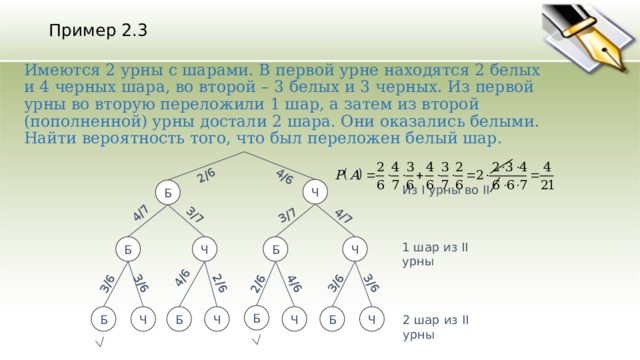
Пример 2.3

Имеются 2 урны с шарами. В первой урне находятся 2 белых и 4 черных шара, во второй – 3 белых и 3 черных. Из первой урны во вторую переложили 1 шар, а затем из второй (пополненной) урны достали 2 шара. Они оказались белыми. Найти вероятность того, что был переложен белый шар.

Из I урны во II

Ч

Б

1 шар из II урны

Б

Ч

Б

Ч

Б

Ч

Б

Ч

Б

Ч

Ч

Б

2 шар из II урны

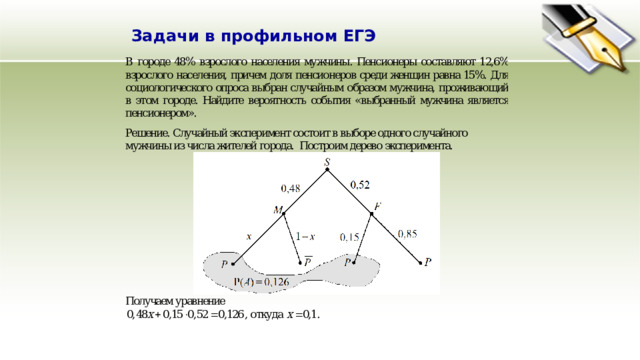
Задачи в профильном ЕГЭ

СПАСИБО ЗА ВНИМАНИЕ.

ВСЕМ УДАЧИ В РАБОТЕ!