Дата
Тема: РЕШЕНИЕ СИСТЕМ НЕРАВЕНСТВ С ОДНОЙ ПЕРЕМЕННОЙ
Задачи: научить решать двойные неравенства с одной переменной.
Ход урока
-
АКТУАЛИЗАЦИЯ ЗНАНИЙ
Самостоятельная работа по вариантам.
-
ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА
Помним, что решением системы неравенств с одной переменной называется значение переменной, при котором выполняется каждое неравенство системы. Решить систему неравенств означает найти все ее решения или доказать, что решений нет.
Вспомним, какой вид имеет двойное неравенство 2
От двойного неравенства лучше переходить к системе. Например, имея двойное неравенство

Для его решения лучше перейти к равносильной системе неравенств
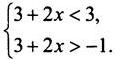
Как получается такой переход? Грубо говоря, двойное неравенство состоит из трех частей, которые разделены двумя знаками неравенства. Рассматриваем отдельно первую и вторую части двойного неравенства, а потом вторую и третью части неравенства, и записываем их в систему. Тогда
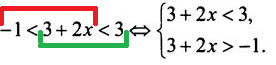
-
ПРАКТИЧЕСКАЯ ЧАСТЬ
Открываем свои тетради и записываем сегодняшнее число и тему урока. Открываем учебник на странице 198 и выполним письменно №892 и №894(а, в).
№ 892. Решить двойное неравенство:
а) 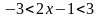 .
.
Для начала распишем его в виде системы (цветом я вам показываю, как двойное разбивается на линейные неравенства, это писать не обязательно):
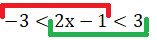

А далее применяем стандартный алгоритм решения системы неравенств с одной переменной.
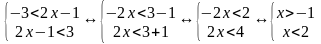
Изобразим решение системы на координатной прямой:
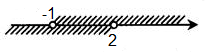
Видим, что две штриховки пересекаются на интервале ( -1; 2), это и будет ответом.
Ответ: 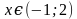 .
.
б) 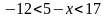 .
.
Для начала распишем его в виде системы:

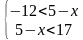
А далее применяем стандартный алгоритм решения системы неравенств с одной переменной.
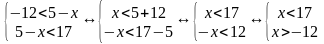
Изобразим решение системы на координатной прямой:
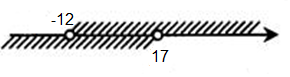
Видим, что две штриховки пересекаются на интервале ( -12; 17), это и будет ответом.
Ответ: 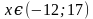 .
.
Самостоятельно выполните № 892 (в).
Все вместе выполним №894(а, в).
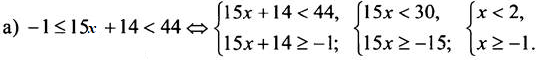 Изобразим решение на координатной прямой:
Изобразим решение на координатной прямой:

Ответ: 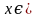 .
.
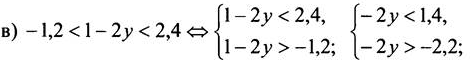
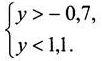
Изобразим решение на координатной прямой:
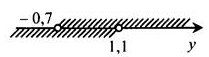
Ответ: 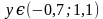 .
.
-
ПОДВЕДЕНИЕ ИТОГОВ УРОКА. РЕФЛЕКСИЯ
Повторите алгоритм решения системы неравенств, подготовьтесь к самостоятельной работе.
Домашнее задание: № 891.








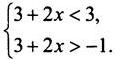

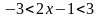 .
.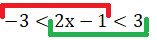

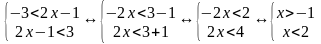

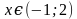 .
.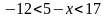 .
.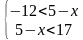
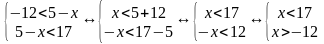

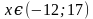 .
.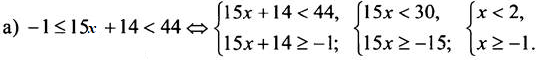 Изобразим решение на координатной прямой:
Изобразим решение на координатной прямой:
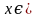 .
.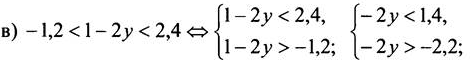
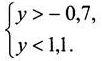
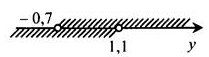
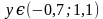 .
.


















