Просмотр содержимого документа
«Решение комбинаторных задач»
Приложени 1.
Решение задач.
 Устный счет:
Устный счет:
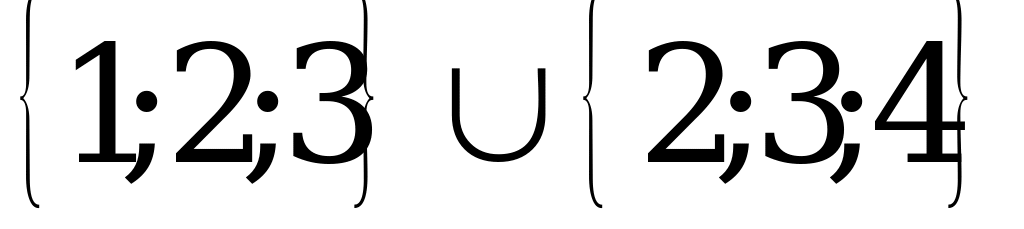 =
= 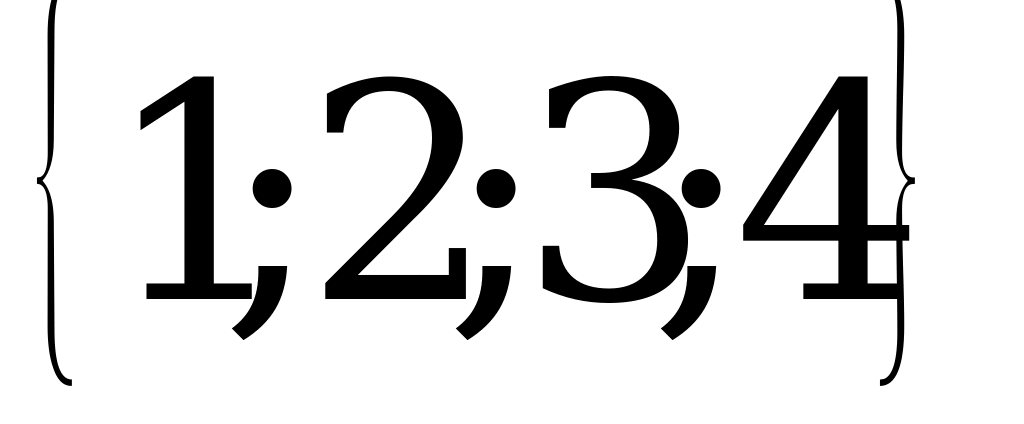
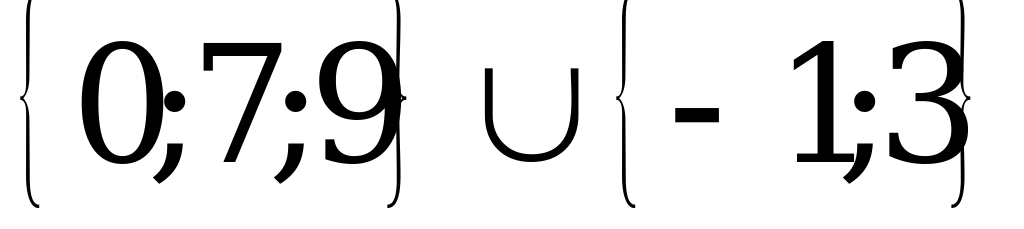 =
=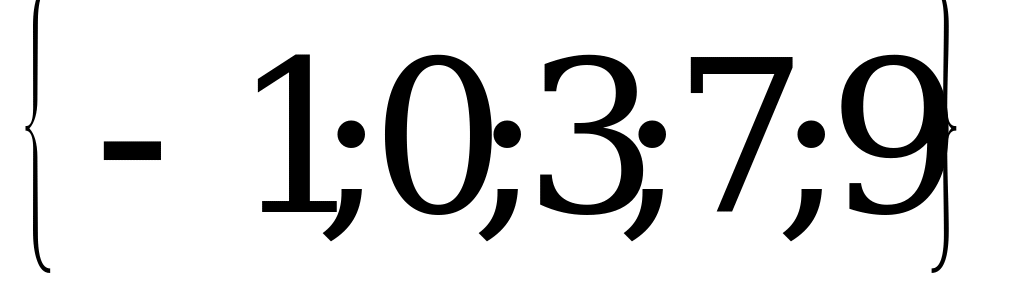
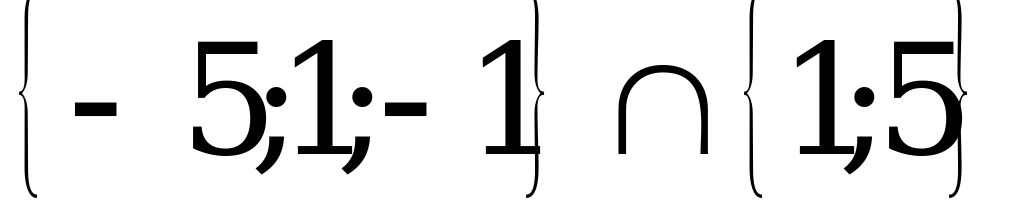 =
=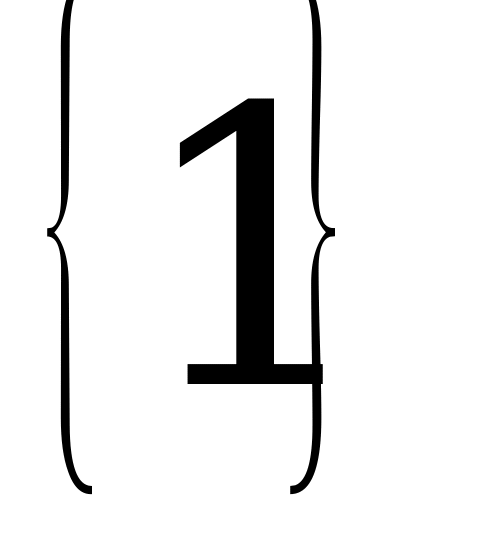
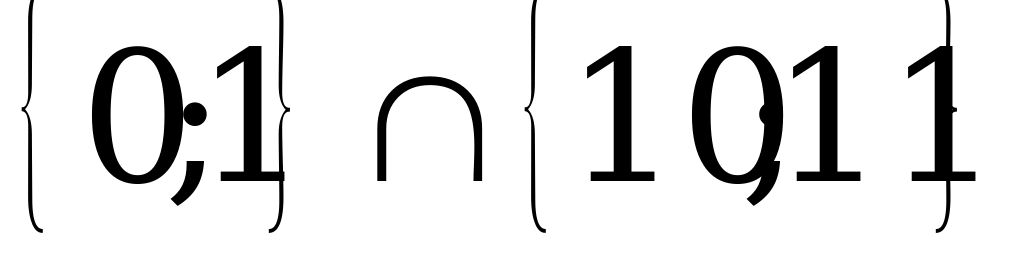 =
=
1! = 1
3! = 1۰2۰3=6
Р2 =2!=1۰2=2
Р4 = 4!=1۰2۰3۰4=24
 =
= 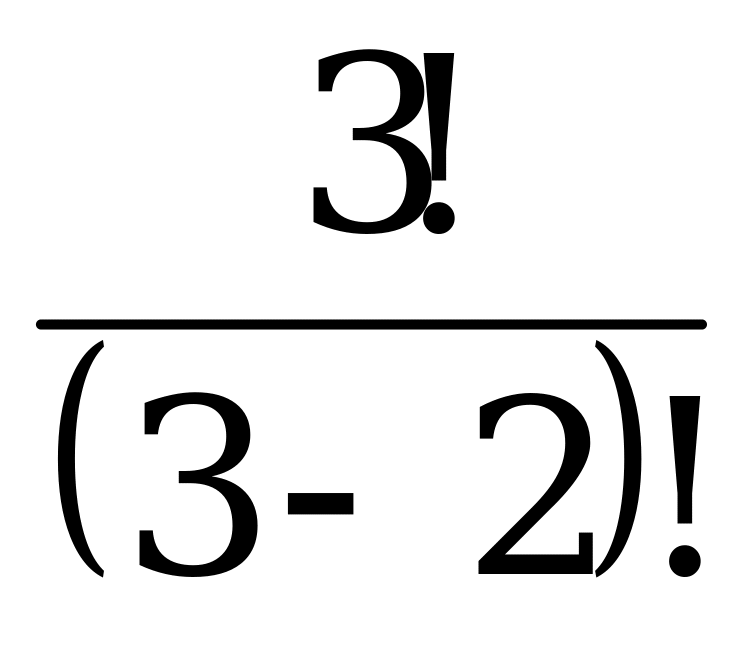 = 3!=6
= 3!=6
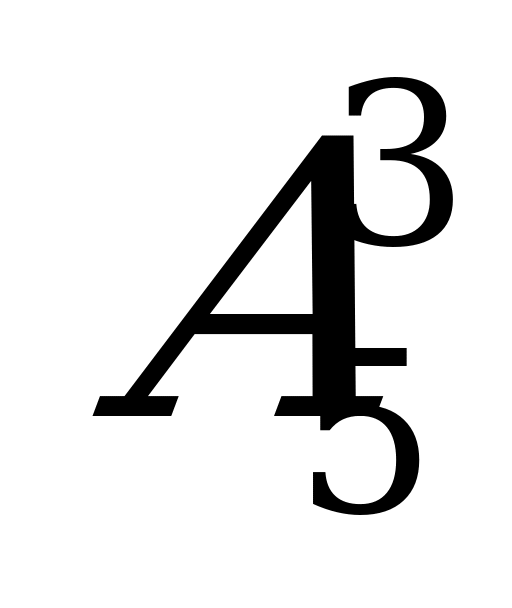 =
= 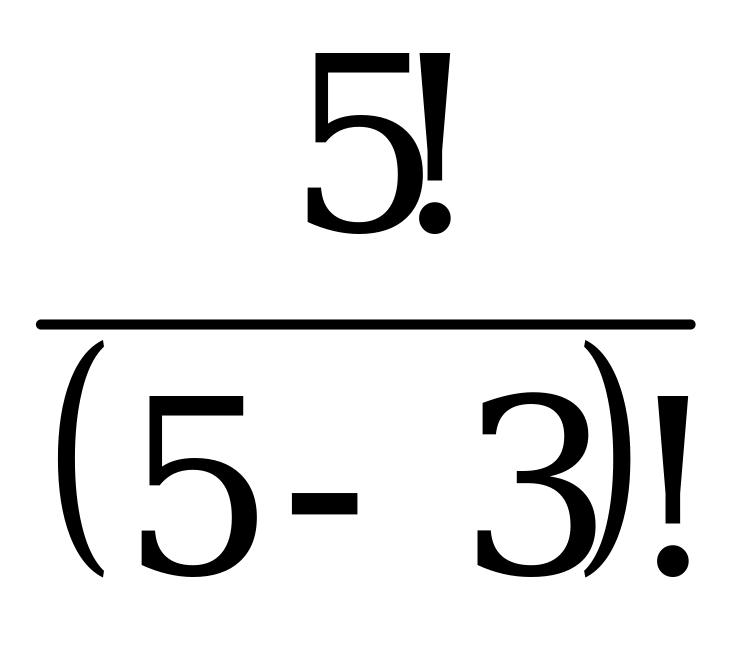 = 60
= 60
 =
= 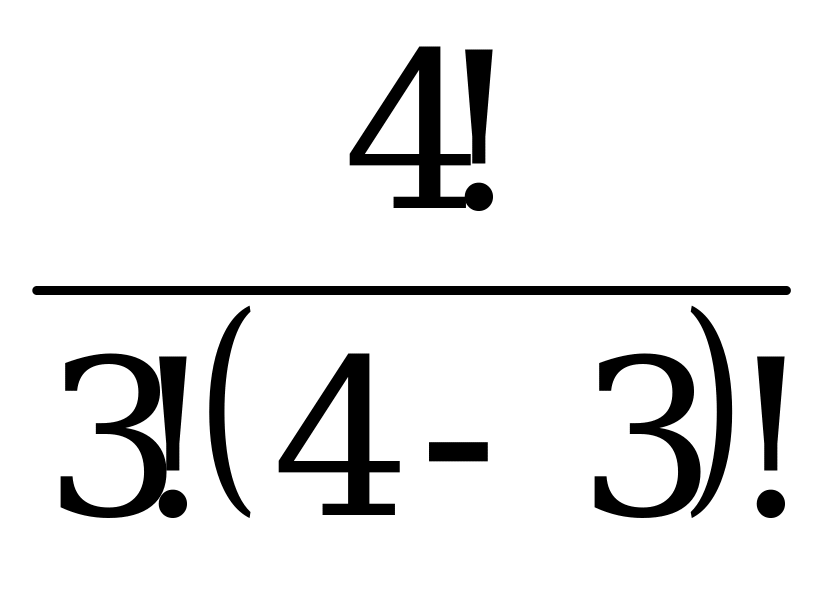 = 4
= 4
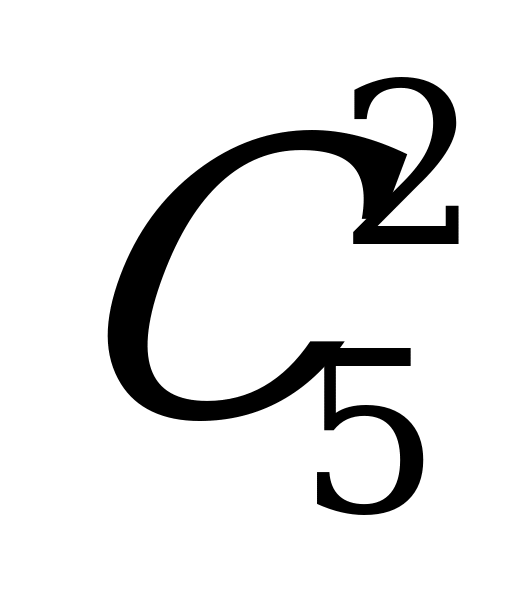 =
= 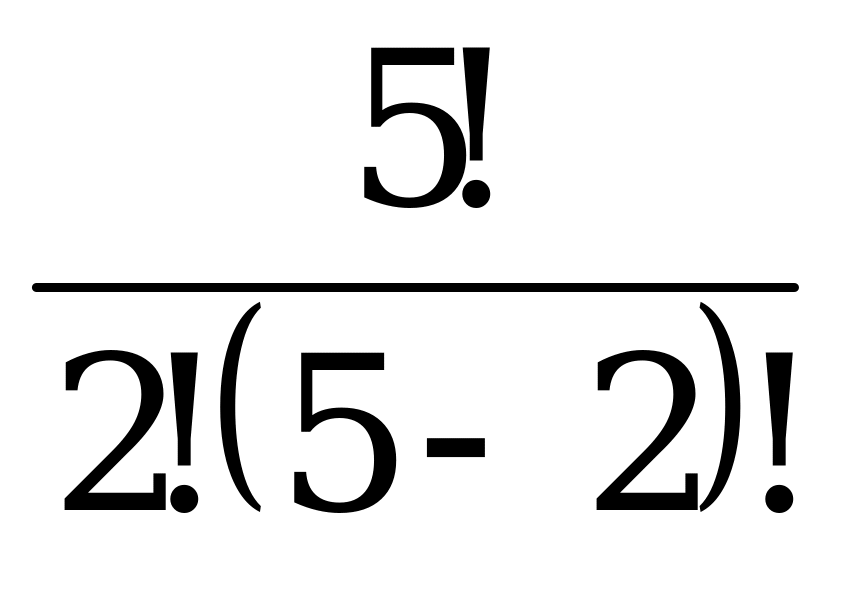 = 1
= 1
Тест
При выборе подходящего комплекта одежды мы пользуемся: перебором.
Комбинаторика изучает: способы решения задач на различные комбинации объектов.
Множество – это: совокупность объектов произвольного рода.
Подсчитывая число маршрутов следования из пункта А в пункт В через пункт С, можно воспользоваться правилом: умножения.
Вычисляя количество всевозможных пар нашей группы необходимо знать формулы: сочетаний.
5! – это: произведение натуральных чисел от 1 до 5 (=120).
Количество способов занять очередь на экзамен n учащимися определяются: перестановкой (n!).
Комбинаторные задачи встречаются в профессиональной деятельности: парикмахера-визажиста, диспетчера автовокзала, завуча школы, экономиста, специалиста по теории кодов.
Задачи на карточках
1. 5۰4=20
2. Я мою руки. Руки мою я. Мою я руки. Я руки мою. Руки я мою. Мою руки я.
3. 3۰5=15
4. 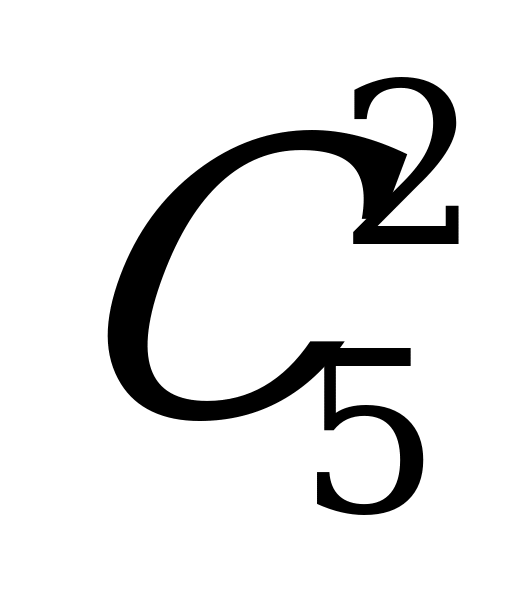 = 10
= 10
5. 2۰5=10
6. Сколько уч-ся занимаются в 2 кружках одновременно? 20+11-(35-10)= 6 (уч-ся)
7.  = 24
= 24
8. 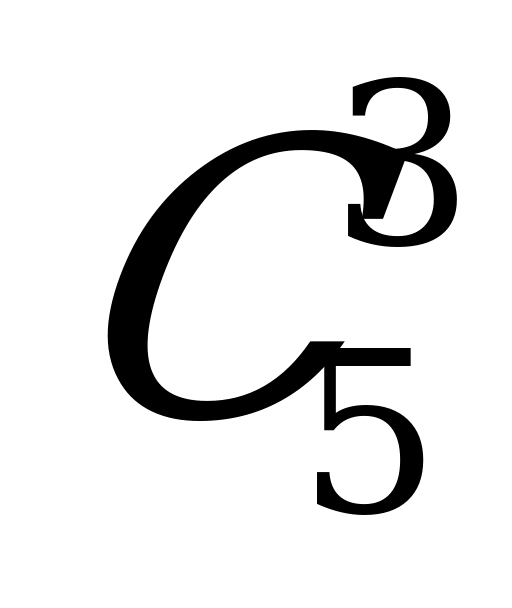 = 10
= 10
9. 1 цифра – выбираем из 3(кроме 0) , 3 цифра – выбираем из 2 (0 или 2, так как число четное), 2 цифра – выбираем из 2 : 3۰2۰2=12 чисел
10. 10۰9۰8۰7=5040 видов расписания
Задачи на закрепление изученного материала
Простые делители 30: 2, 3, 5. Тогда 30 = 235, = 253, =325, =352, =523, =532 – всего 6 способов.
Из одной вершины можно провести 10-3=7 диагоналей, 10۰7:2=35 диагоналей
Составим уравнение (х – количество друзей)
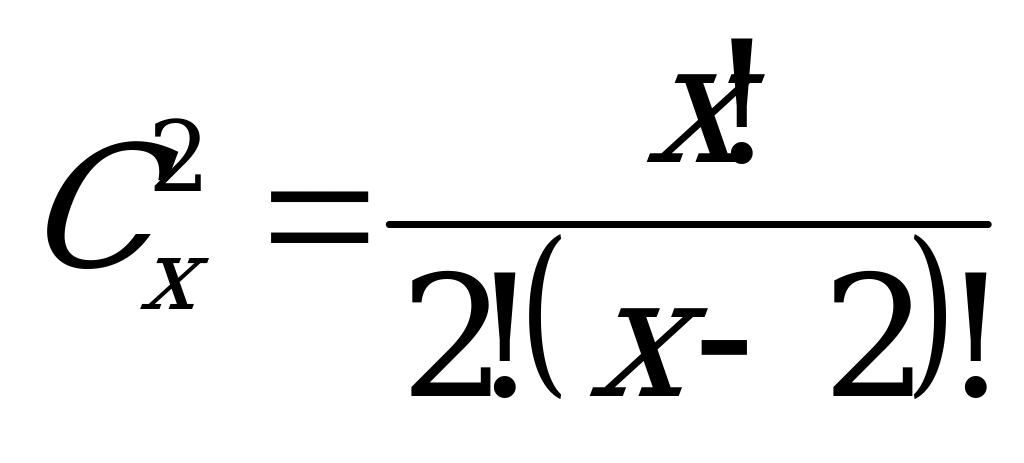 , х(х-1)= 30, х2-х-30=0, х1=6, х2= -5
, х(х-1)= 30, х2-х-30=0, х1=6, х2= -5
Значит, было 6 друзей.
 = 4۰5=20
= 4۰5=20
Согласно условию только два языка не знает никто. Пусть х человек знают все 3 языка, тогда верно 85+80+75-3х+х =100, х = 70.
Пример призового балла за работу на уроке.
(Желательно распечатать на цветной бумаге, внутри квадратика можно писать фамилию ученика и ставить подпись учителя, а сам балл вклеивать в тетрадь)
| Т Ы ЛУЧШИЙ! Ы ЛУЧШИЙ! | Т Ы ЛУЧШИЙ! Ы ЛУЧШИЙ! | Т Ы ЛУЧШИЙ! Ы ЛУЧШИЙ! | Т Ы ЛУЧШИЙ! Ы ЛУЧШИЙ! |






 Устный счет:
Устный счет: Ы ЛУЧШИЙ!
Ы ЛУЧШИЙ!









