Решение логических задач

Логические задачи

Подготовила

Ученица 7 Б класса

Рожкова Дарья

«Предмет математики настолько серьезен,

что нельзя упускать случая, сделать его

немного занимательным»

Блез Паскаль

• Французский философ, физик, математик Блез Паскаль – создатель первой в мире вычислительной машины. В его честь назван известный язык программирования «Паскаль».

• Древнегреческий философ и ученый Аристотель (384-322 гг. до н. э.) впервые разработал теорию дедукции, то есть теорию логического вывода.

• Древнегреческий математик Евклид (330-275 гг. до н. э.) впервые предпринял попытку упорядочить накопившиеся к тому времени обширные сведения по геометрии.

• Джордж Буль (1815-1864 гг. ) применил к логике методы современной ему алгебры – язык символов и формул, составление и решение уравнений. Им была создана своеобразная алгебра - алгебра логики. Он разработал алгебру логики «Исследования законов мышления» (1854), основу функционирования цифровых компьютеров.

Эти известные люди и многие другие с большим интересом занимались поиском методов решения логических задач.

• Цель:
• Освоить методы решения логических задач.
• Задачи:
• 1. Ознакомиться с понятиями «Логика» и «Логические задачи»
• 2. Изучение и разбор основных методов решения логических задач

• Слово «логика» означает совокупность правил, которым подчиняется процесс мышления. Сам термин «логика» происходит от древнегреческого «logos», означающего «слово, мысль, понятие, рассуждение, закон».

• Решать логические задачи очень увлекательно.
• Логические задачи от обычных задач отличаются тем, что не требуют вычислений. Чаще всего в таких задачах создается ситуация, выход из которой может быть найден, если мы тщательно изучим ситуацию и сделаем ряд выводов, иначе говоря, логическим методом, с помощью логических рассуждений.

• Известны различные приемы и методы решения логических задач:
• - Метод рассуждений
• - Метод таблиц
• - Метод графов
• - Метод блок-схем
• -Метод кругов Эйлера.
• -Истинностные задачи
• -Задачи, решаемые с конца

Метод таблиц

• Основной прием, который используется при решении текстовых логических задач, заключается в построении таблиц. Таблицы не только позволяют наглядно представить условие задачи или ее ответ, но в значительной степени помогают делать правильные логические выводы в ходе решения задачи.

Задача 1

• Три мальчика Артем, Дима и Саша пришли на праздник в красной, зеленой и синей рубашках. Их туфли были тех же цветов. У Артема цвета рубашки и туфель совпадали. У Димы ни туфли, ни рубашка не были красными. Саша был в зеленых туфлях и в рубашке другого цвета. Как были одеты мальчики?

Решение

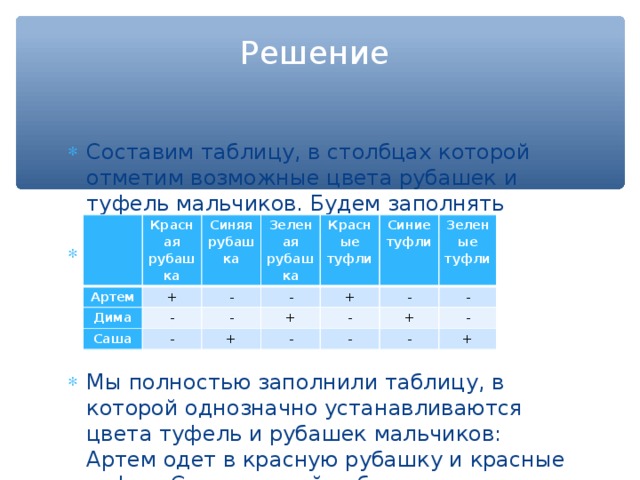
• Составим таблицу, в столбцах которой отметим возможные цвета рубашек и туфель мальчиков. Будем заполнять таблицу, используя условие задачи.

• Мы полностью заполнили таблицу, в которой однозначно устанавливаются цвета туфель и рубашек мальчиков: Артем одет в красную рубашку и красные туфли, Саша в синей рубашке и зеленых туфлях, Дима в зеленой рубашке и туфлях синего цвета.

Артем

Красная рубашка

Синяя рубашка

Дима

+

Зеленая рубашка

Саша

-

-

-

Красные туфли

-

-

+

Синие туфли

+

+

Зеленые туфли

-

-

-

-

-

+

-

-

+

Задача 2

• В одном дворе живут четыре друга. Вадим и шофер старше Сергея, Николай и слесарь занимаются боксом, электрик-младший из друзей, по вечерам Антон и токарь играют в домино против Сергея и электрика. Определите профессии каждого из друзей.
• По ранее рассмотренному принципу заполним вторую таблицу

шофер

Вадим

слесарь

Сергей

-

токарь

Николай

-

-

электрик

+

+

-

Антон

-

+

-

-

-

-

-

-

+

-

Метод кругов Эйлера

• Этот метод является еще одним наглядным и довольно интересным способом решения логических задач. В основе этого метода лежит построение знаменитых кругов Эйлера-Венна, задачи, в которых требуется найти некоторое пересечение множеств или их объединение, соблюдая условия задачи. Разберем пример применения данного метода.

Задача 1

• Из 52 школьников 23 собирают значки, 35 собирают марки, а 16 — и значки, и марки. Остальные не увлекаются коллекционированием. Сколько школьников не увлекается коллекционированием?

Решение

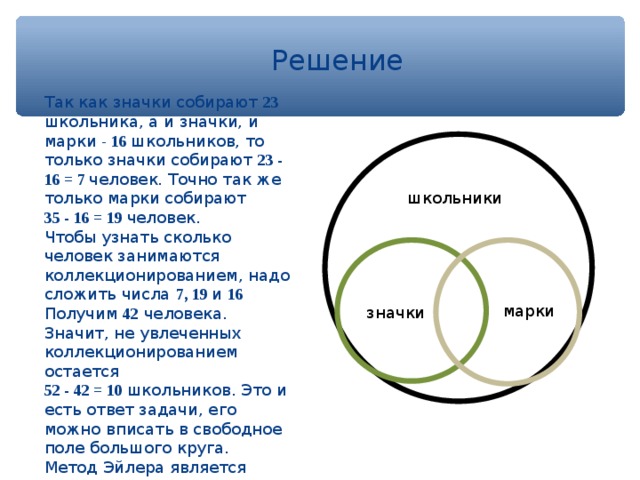
Так как значки собирают 23 школьника, а и значки, и марки - 16 школьников, то только значки собирают 23 - 16 = 7 человек. Точно так же только марки собирают

35 - 16 = 19 человек.

Чтобы узнать сколько человек занимаются коллекционированием, надо сложить числа 7, 19 и 16 Получим 42 человека. Значит, не увлеченных коллекционированием остается

52 - 42 = 10 школьников. Это и есть ответ задачи, его можно вписать в свободное поле большого круга.

Метод Эйлера является незаменимым при решении некоторых задач, а также значительно упрощает рассуждения.

школьники

марки

значки

Задача 2

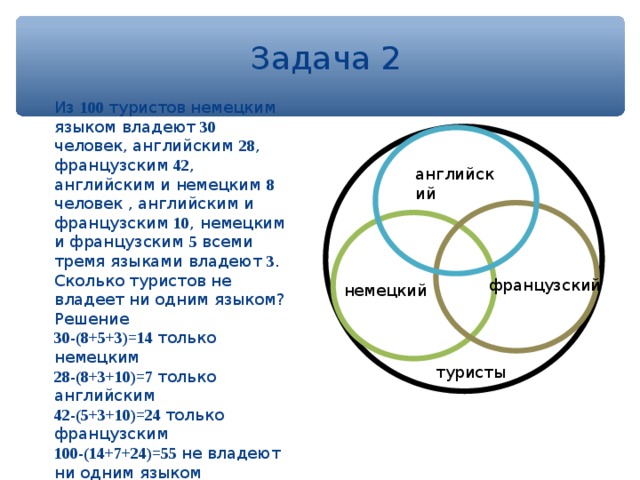
Из 100 туристов немецким языком владеют 30 человек, английским 28 , французским 42 , английским и немецким 8 человек , английским и французским 10 , немецким и французским 5 всеми тремя языками владеют 3 . Сколько туристов не владеет ни одним языком?

Решение

30-(8+5+3)=14 только немецким

28-(8+3+10)=7 только английским

42-(5+3+10)=24 только французским

100-(14+7+24)=55 не владеют ни одним языком

английский

французский

немецкий

туристы

Задачи решаемые с конца

(от обратного)

• Такие задачи очень часто ребята задают друг другу в виде головоломок на задуманное число. Задачи решаются методом математических вычислений, основанных на конечном результате в условии.

Задача 1

• Андрей задумал число, прибавил к нему 5 , потом разделил сумму на 3 , умножил на 4 , отнял 6 , разделил на 7 и получил число 2 . Какое число задумал Андрей?
• Решение:
• 2х7=14
• 14+6=20
• 20˸4=5
• 5х3=15
• 15-5=10
• Ответ: Андрей задумал число 10

Задача 2

• На озере расцвела лилия. Каждый день число цветков удваивалось и на 20 -й день все озеро покрылось цветами. За сколько дней покрылась цветами половина озера?
• Решение.
• Начнем с конца. Так как каждый день число цветков удваивается, а на 20 -й день все озеро покрылось цветами, то половина его была покрыта цветами за один день до того, т.е. на 19 -й день.
• Ответ: за 19 дней.

Задача 3

• Группа туристов отправилась в поход. В первый день они прошли треть пути во второй-треть остатка, в третий-треть нового остатка. В результате им осталось пройти 32 км. Сколько километров был маршрут туристов?
• Решение
• 32:2/3=48 (км)-последний остаток
• 48:2/3=72 (км)- 2/3 всего маршрута
• 72:2/3=108 (км)-весь путь
• Ответ: 108 км

Задача 4

• Отцу и сыну вместе 65 лет. Сын родился когда отцу было 25 лет. Какой возраст у отца, а какой у сына
• Решение
• 65-25=40 (лет)-удвоенный возраст сына
• Значит сыну 20 лет, а отцу 45
• Ответ: сыну 20 , а отцу 45

Истинноностные задачи

• При решении задач данного типа лучше всего использовать метод рассуждений. Он позволяет проводить рассуждения, используя последовательно все условия задачи, и приходить к выводу, который и будет являться ответом задачи.

Задача 1

• Три друга Коля, Олег и Петя играли во дворе, и один из них случайно разбил мячом оконное стекло. Коля сказал: «Это не я разбил стекло». Олег сказал: «Это Петя разбил стекло». Позднее выяснилось, что одно из этих утверждений верное, а другое — нет. Кто из мальчиков разбил стекло?
• Решение.
• Предположим, что Олег сказал правду, тогда и Коля сказал правду, а это противоречит условию задачи. Следовательно, Олег сказал неправду, а Коля — правду. Из их утверждений следует, что стекло разбил Олег.

Метод рассуждений

• Способ рассуждений - самый примитивный способ. Этим способом решаются самые простые логические задачи. Его идея состоит в том, что мы проводим рассуждения, используя последовательно все условия задачи, и приходим к выводу, который и будет являться ответом задачи. Познакомиться с этим методом можно на следующем примере.

Задача 1

• Четыре брата Юра, Петя, Вова, Коля учатся в 1,2,3,4 классах. Петя - отличник, младшие братья стараются брать с него пример. Вова учится в 4 классе. Юра помогает решать задачи брату. Кто в каком классе учиться?
• Решение.
• Вова учится в 4 классе, а младшие братья берут пример с Пети, значит Петя учится в 3 классе, Юра помогает решать задачи брату, значит он учится во 2 классе, следовательно в 1 классе учится Коля.
• Ответ: Вова учится в 4 классе, Петя в 3 классе, Юра во 2 классе, а Коля в 1 классе.

Задача 2

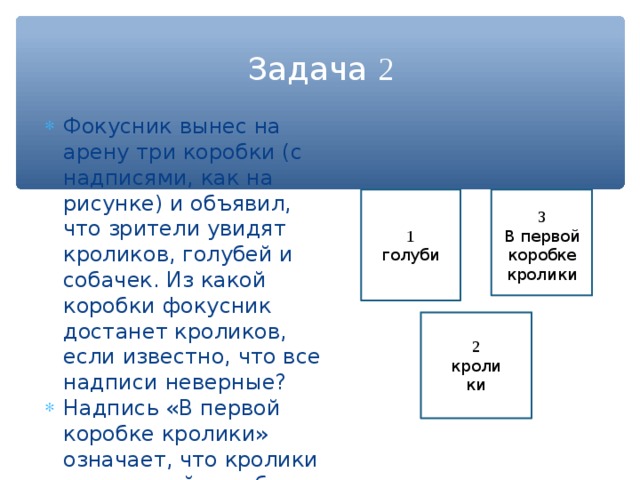
• Фокусник вынес на арену три коробки (с надписями, как на рисунке) и объявил, что зрители увидят кроликов, голубей и собачек. Из какой коробки фокусник достанет кроликов, если известно, что все надписи неверные?
• Надпись «В первой коробке кролики» означает, что кролики не в первой коробке. Надпись «Кролики» (на второй коробке) означает, что кролики не во второй коробке. Значит, кролики в коробке под номером 3 .

3

В первой коробке кролики

1

голуби

2

кролики

• Логические задачи — пожалуй, самый эффективный инструмент для развития логики и мышления, как у детей, так и у взрослых.
• Такие задачи находят свое практическое применение в педагогике, медицине, информатике, криминалистике, юриспруденции и других сферах.

• Но, к сожалению, не все люди относятся к этому всерьез.

«

«Многие люди только мыслят, что мыслят.

Им неприятен мыслительный процесс:

для этого нужен навык и известные усилия,

а зачем усилия, когда можно без»

Американский поэт-сатирик Огден Неш.

Источники

• Я. И. Перельман «101 головоломка»
• Ведущий образовательный портал России «Инфоурок»
• Свободная энциклопедия «Википедия»
• Образовательный портал для подготовки к работам «Решу ВПР»
• Образовательная платформа для развития логического мышления и математических способностей «Logiclike»